சாய்வுகள் | ஆயத்தொலை வடிவியல் - கோட்டின் சாய்வு | 10th Mathematics : UNIT 5 : Coordinate Geometry
10வது கணக்கு : அலகு 5 : ஆயத்தொலை வடிவியல்
கோட்டின் சாய்வு
கோட்டின் சாய்வு (Inclination of a line)
கோட்டின் சாய்வு அல்லது சாய்வுக் கோணம் (inclination of a line) என்பது X அச்சின் மிகை திசைக்கும், நேர்க்கோட்டிற்கும் இடையே, கடிகார முள்ளின் எதிர் திசையில் அமைந்த கோணம் ஆகும். சாய்வுக் கோணம் θ எனக் குறிக்கப்படுகிறது.
குறிப்பு
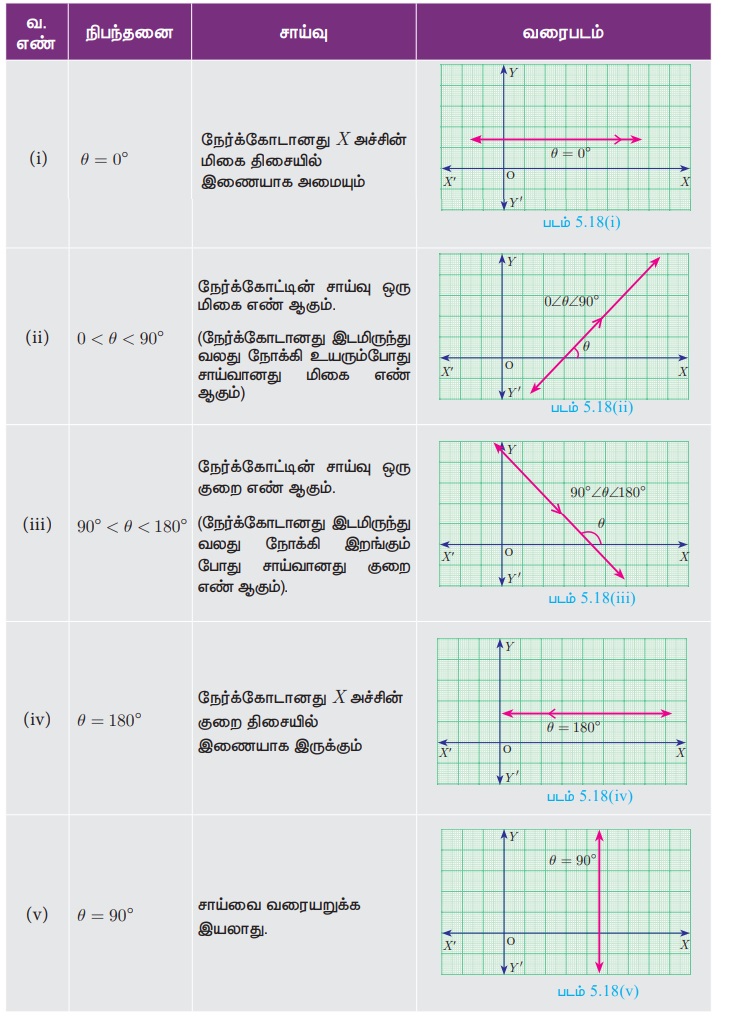
• X அச்சு மற்றும் X அச்சுக்கு இணையான நேர்க்கோடுகளின் சாய்வுக்கோணம் 0° ஆகும்.
• Y அச்சு மற்றும் Y அச்சுக்கு இணையான நேர்க்கோடுகளின் சாய்வுக் கோணம் 90° ஆகும்.
1. நேர்க்கோட்டின் சாய்வு (Slope of a Straight line)
சாலைகளை அமைக்கும்போது, எவ்வளவு சாய்வாகச் சாலை இருக்கவேண்டும் என்பதை அறிந்துகொள்ளவேண்டும். அதேபோல மாடிப் படிக்கட்டுகள் அமைக்கும்போதும், அதன் சாய்வுத் தன்மையைக் கருத்தில் கொள்ள வேண்டும். இந்தச் சாய்வுத் தன்மையினால் சாதாரணச் சாலையில் பயணிப்பதைவிட மலை அல்லது மேம்பாலம் ஆகியவற்றில் பயணிப்பது கடினமானதாக உணர்கிறோம். இவையாவிலும் முக்கிய அம்சமாக இருப்பது "சாய்வுத் தன்மை" (steepness) ஆகும். இந்தச் சாய்வுத் தன்மையானது சாய்வு அல்லது சாய்வின் அளவு (Slope or gradiant) என்று அழைக்கப்படுகிறது.

சாய்வு என்ற கருத்தானது பொருளாதாரத்தில் முக்கியப் பங்கு வகிக்கிறது. ஒரு குறிப்பிட்ட காலத்தில் ஒரு பொருளின் விலைக்கேற்ப அதன் தேவை மாறுபடுவதைக் கணக்கிடுவதில் இந்தக் கருத்து பயன்படுகிறது. சாய்வானது சாய்வுத் தன்மை (steepness) மற்றும் திசை (Direction) என்ற இரு காரணிகளை உள்ளடக்கியதாகும்.
வரையறை
நேர்குத்தற்ற நேர்க்கோட்டின் (non-vertical line) சாய்வுக் கோணம் θ எனில், tan θ என்பது அக்கோட்டின் சாய்வு ஆகும். இதை m எனக் குறிக்கலாம்.
எனவே, நேர்க்கோட்டின் சாய்வு m = tan θ, 0 ≤ θ ≤ 180°, θ ≠ 90° ஆகும்.
இரு புள்ளிகள் கொடுக்கப்பட்டால் நேர்க்கோட்டின் சாய்வைக் காணல்
சாய்வு m = tan θ

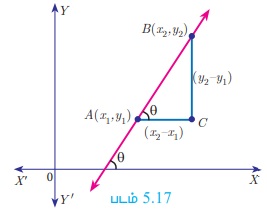
(x 1 , y1 ) மற்றும் (x 2 , y2 ), x 1 ≠ x2 என்ற புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோட்டின் சாய்வு 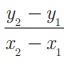 ஆகும்.
ஆகும்.
குறிப்பு
செங்குத்துக் கோட்டின் சாய்வு வரையறுக்கப்பட இயலாது (Undefined).
சாய்வுகளின் மதிப்புகள்
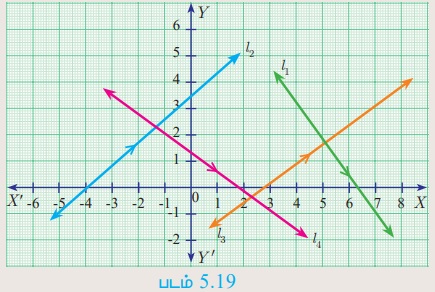
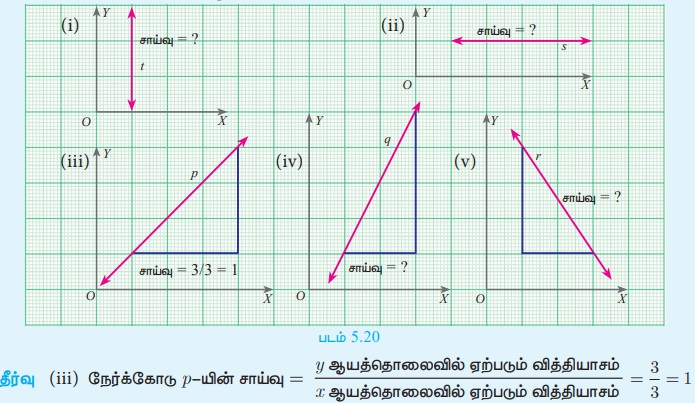
செயல்பாடு 3
வரைபடமானது l1, l2, l3 மற்றும் l4 என்ற நான்கு நேர்க்கோடுகளைக் கொண்டுள்ளது
(i) மிகைச் சாய்வு கொண்ட நேர்க்கோடுகள் எவை?
(ii) குறைச் சாய்வு கொண்ட நேர்க்கோடுகள் எவை?
முன்னேற்றச் சோதனை
கீழே கொடுக்கப்பட்ட நேர்க்கோடுகளின் சாய்வைக் கண்டுபிடிக்க. கணக்கு (iii)-ன் தீர்வு தரப்பட்டுள்ளது.
2. இணைகோடுகளின் சாய்வுகள் (Slopes of parallel lines)
இரண்டு நேர்குத்தற்ற கோடுகளின் சாய்வுகள் சமமாக இருந்தால், இருந்தால் மட்டுமே அவை இணையாக இருக்கும்.
l1 மற்றும் l2 என்ற இரு நேர்குத்தற்ற கோடுகளின் சாய்வுகள் முறையே m1 மற்றும் m2 என்க.
நேர்க்கோடுகள் X அச்சின் மிகை திசையில் ஏற்படுத்தும் சாய்வுக் கோணம் θ1 மற்றும் θ2 என்க.
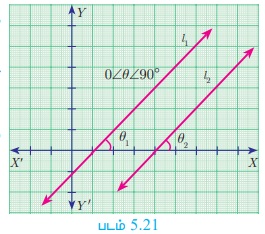
l1 மற்றும் l2 இணை கோடுகள் எனக் கொள்க.
θ1 = θ2 (θ1 , θ2 என்பன ஒத்த கோணங்கள் என்பதால்)
tan θ1= tan θ2
m1= m2
ஆகவே, சாய்வுகள் சமம்.
எனவே, நேர்குத்தற்ற இணையான கோடுகளின் சாய்வுகள் சமம்.
மறுதலையாக
சாய்வுகள் சமம் என்க. ஆகவே m1= m2
tan θ1= tan θ2
θ1= θ2 (0 ≤ θ1 ≤ 180°, 0 ≤ θ2 ≤ 180° என்பதால்)
அதாவது ஒத்த கோணங்கள் சமம்.
இதிலிருந்து, l1 மற்றும் l2 இணை கோடுகள் ஆகும்.
எனவே, இரு நேர்குத்தற்ற கோடுகளின் சாய்வுகள் சமமெனில் அக்கோடுகள் இணையாகும். ஆகையினால் நேர்குத்தற்ற இரு கோடுகள் இணையாக இருக்க வேண்டுமாயின், அக்கோடுகளின் சாய்வுகள் சமமாக இருக்க வேண்டும்.
3. செங்குத்துக்கோடுகளின் சாய்வுகள் (Slopes of perpendicular lines)
இரண்டு நேர்குத்தற்ற கோடுகளின் சாய்வுகளான m1 m2 இவற்றின் பெருக்கல் பலன் அதாவது m1= m2 = -1 ஆக இருந்தால், இருந்தால் மட்டுமே, அக்கோடுகள் செங்குத்தாக இருக்கும்.
l1 மற்றும் l2 ஆகிய நேர்குத்தற்ற இருகோடுகளின் சாய்வுகள் முறையே m1 மற்றும் m2 என்க. அவற்றின் சாய்வுக் கோணங்கள் முறையே θ1 மற்றும் θ2 என்க.
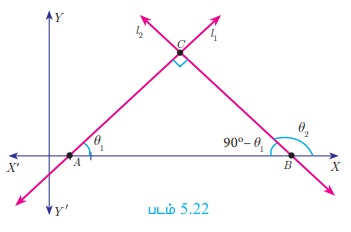
மேலும் m1 = tan θ1 மற்றும் m2 = tan θ2
முதலில், l1 மற்றும் l2 ஒன்றுக்கொன்று செங்குத்து எனக் கொள்க.
∠ABC = 90° − θ1 (ΔABC -யின் கோணங்களின் கூடுதல் 180°)
அடுத்தடுத்த கோணங்கள் θ2 மற்றும் 90° − θ1 ஆகியவற்றைக் கொண்டு l2 என்ற நேர்க்கோட்டின் சாய்வைக் கணக்கிடுக.
tan θ2 = − tan(90° − θ1 )
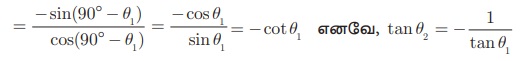
tan θ1. tan θ2 = −1
m1m2 = −1
இதிலிருந்து, l1, l2 என்ற இரு கோடுகள் ஒன்றுக்கொன்று செங்குத்து எனில், m1m2 = −1 ஆகும்.
உங்களுக்குத் தெரியுமா?
எந்த ஒரு முக்கோணத்திற்கும் அதன் வெளிக்கோணமானது உள் எதிர் கோணங்களின் கூடுதலுக்குச் சமம்
மறுதலையாக,
l1, l2 என்ற நேர்குத்தற்ற இரு கோடுகளின் சாய்வுகள் முறையே m1 மற்றும் m2 என்க. மேலும், m1 m2 = -1 எனக் கொள்க.
m1 = tan θ 1 , m2 = tan θ2 என்பதால் நாம் பெறுவது,
tan θ1 tan θ2 = −1
tan θ1 = −1/ tan θ2
tan θ1 = −cot θ2
tan θ1 = −tan (90° - θ2)
tan θ1 = tan (-(90° - θ2)) = tan (θ2 - 90°)
θ1 = θ2 - 90° (0 ≤ θ1 ≤ 180°, 0 ≤ θ2 ≤ 180° என்பதால்)
θ2 = 90° + θ1
ஆனால், ΔABC யில், θ2 = ∠C + θ1
எனவே, ∠C = 90°
ஆகவே, l1 மற்றும் l2 ஆகிய கோடுகள் ஒன்றுக்கொன்று செங்குத்து ஆகும்
குறிப்பு
நேர்குத்தற்ற இரு நேர்க்கோடுகள், l1, l2 ஆகியவற்றின் சாய்வுகள் முறையே m1, m2 எனில்,
(i) l1 ஆனது l2 -க்கு இணை எனில், எனில் m1 = m2
(ii) l1, l2 ஒன்றுக்கொன்று செங்குத்து எனில், m1, m2 = -1
எடுத்துக்காட்டு 5.8
(i) ஒரு கோட்டின் சாய்வுக் கோணம் 30° எனில், அக்கோட்டின் சாய்வைக் காண்க. (ii) ஒரு கோட்டின் சாய்வு √3 எனில், அக்கோட்டின் சாய்வுக் கோணம் காண்க.
தீர்வு
(i) இங்கு θ = 30°
சாய்வு m = tan θ
எனவே, சாய்வு m = tan 30° = 1 /√3
(ii) சாய்வு m = √3, θ என்பது கோட்டின் சாய்வுக் கோணம் என்க.
tan θ = √3
θ = 60°
சிந்தனைக் களம்
X அச்சு மற்றும் Y அச்சு ஆனது ஒன்றுக்கொன்று செங்குத்தானவை. இங்கு m1, m2 = -1 என்ற நிபந்தனை உண்மையாகுமா?
எடுத்துக்காட்டு 5.9
கொடுக்கப்பட்ட புள்ளிகளை இணைக்கும் நேர்க்கோட்டின் சாய்வைக் காண்க.
(i) (-6, 1) மற்றும் (-3, 2)
(ii) (-1/3, ½), மற்றும் (2/7, 3/7)
(iii) (14, 10) மற்றும் (14, -6)
தீர்வு
(i) (-6, 1) மற்றும் (-3, 2)
சாய்வு 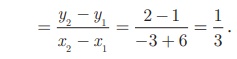
(ii) (-1/3, 1/2), மற்றும் (2/7, 3/7)
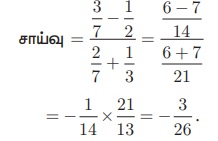
(iii) (14, 10) மற்றும் (14, - 6)
சாய்வு = 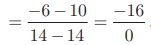
⸫ சாய்வை வரையறுக்க இயலாது.
முன்னேற்றச் சோதனை
விடுபட்டவற்றைப் பூர்த்தி செய்க.
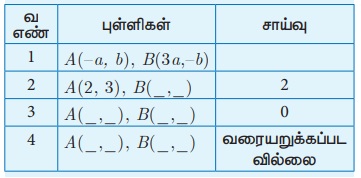
எடுத்துக்காட்டு 5.10
(-2, 2), (5, 8) என்ற புள்ளிகள் வழிச் செல்லும் நேர்க்கோடு r மற்றும் (-8, 7), (-2, 0) ஆகிய புள்ளிகள் வழிச் செல்லும் நேர்க்கோடு s ஆகும் எனில், நேர்க்கோடு r-ஆனது நேர்க்கோடு s - க்கு செங்குத்தாக அமையுமா?
தீர்வு

அதாவது, m1m2 = −1
எனவே, நேர்க்கோடு r ஆனது, நேர்க்கோடு s -க்கு செங்குத்தாக அமையும்.
எடுத்துக்காட்டு 5.11
(3,-2), (12,4) என்ற புள்ளிகள் வழிச் செல்லும் நேர்க்கோடு p மற்றும் (6,- 2) மற்றும் (12,2) என்ற புள்ளிகள் வழிச் செல்லும் நேர்க்கோடு q ஆகும். p ஆனது q -க்கு இணையாகுமா?
தீர்வு
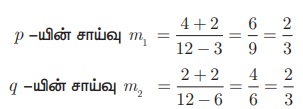
இதிலிருந்து, நேர்க்கோடு p-யின் சாய்வு = நேர்க்கோடு q-யின் சாய்வு. எனவே, நேர்க்கோடு p-யானது நேர்க்கோடு q-க்கு இணை ஆகும்.
எடுத்துக்காட்டு 5.12
(-2,5), (6,-1) மற்றும் (2,2) ஆகிய புள்ளிகள் ஒரு கோடமைந்த புள்ளிகள் எனக் காட்டு.
தீர்வு
A(-2,5), B(6,-1) மற்றும் C(2,2) என்பன கொடுக்கப்பட்ட புள்ளிகள் ஆகும்.
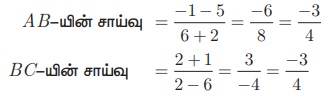
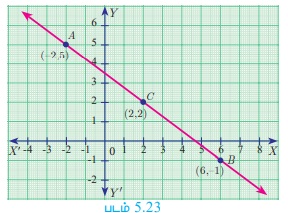
AB-யின் சாய்வு = BC -யின் சாய்வு
எனவே, A, B, C என்ற புள்ளிகள் ஒரே நேர்க்கோட்டின் மேல் அமைந்துள்ளன. ஆகவே, A, B, C என்பன ஒரு கோடமைந்த புள்ளிகள் ஆகும்.
எடுத்துக்காட்டு 5.13
A(1,- 2), B(6,- 2), C(5,1) மற்றும் D(2,1) என்பன நான்கு புள்ளிகள் எனில்,
(i) (a) AB (b) CD என்ற கோட்டுத் துண்டுகளின் சாய்வுகளைக் காண்க (ii) (a) BC (b) AD என்ற கோட்டுத் துண்டுகளின் சாய்வுகளைக் காண்க (iii) விடைகளிலிருந்து நீங்கள் அறிவது என்ன?
தீர்வு

(iii) AB-யின் சாய்வும், CD–ன் சாய்வும் சமமாக இருப்பதால், அவைகள் இணையாகும். இதேபோல் AD–யின் சாய்வும், BC-யின் சாய்வும் சமம் இல்லை. எனவே, இவை இணை இல்லை.
ஆகையால், நாற்கரம் ABCD ஆனது ஒரு சரிவகம் என அறியலாம்
உங்களுக்குத் தெரியுமா?
நாற்கரத்தின் எதிரெதிரே உள்ள பக்கங்களின் சாய்வுகள் சமமாக இருந்தால், அந்நாற்கரமானது இணைகரம் ஆகும்.
எடுத்துக்காட்டு 5.14
கீழே கொடுக்கப்பட்ட மக்கள் தொகைப் பெருக்கம் (கோடிகளில்) மற்றும் ஆண்டிற்கான வரைபடத்தில் AB என்ற நேர்க்கோட்டின் சாய்வைக் காண்க. மேலும் 2030-ம் ஆண்டிற்கான மக்கள் தொகையையும் கணக்கிடுக.
தீர்வு
A(2005,96) மற்றும் B(2015,100) என்பன நேர்க்கோடு AB-யின் புள்ளிகள் ஆகும்.
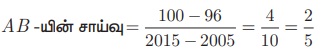
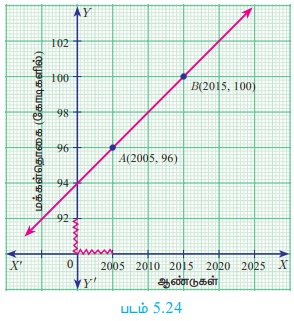
2030 யில் மக்கள் தொகை வளர்ச்சி k கோடிகள் என்க.
C(2030, k) என்பது AB-யின் மீதுள்ள புள்ளி எனக் கொள்க
AC-யின் சாய்வு = AB-யின் சாய்வு
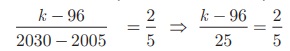
k - 96 = 10
k = 106
எனவே, 2030 -யில் மக்கள் தொகை 106 கோடிகள்
எடுத்துக்காட்டு 5.15
பிதாகரஸ் தேற்றத்தைப் பயன்படுத்தாமல், (1, -4), (2, -3) மற்றும் (4,-7) என்ற முனைப் புள்ளிகள் ஒரு செங்கோண முக்கோணத்தை அமைக்கும் எனக் காட்டுக.
தீர்வு
A(1,- 4), B(2,- 3) மற்றும் C(4,- 7) ஆகியன முக்கோணத்தின் முனைப் புள்ளிகள் என்க.
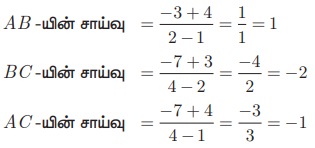
AB-யின் சாய்வு × AC-யின் சாய்வு = (1) (-1) = -1
ஆகவே, AB ஆனது AC-க்கு செங்குத்தாகும். ∠A = 90°
எனவே, ΔABC ஆனது செங்கோண முக்கோணம் ஆகும்.
சிந்தனைக்களம்
நமது அன்றாட வாழ்வில் சாய்வுகள் பயன்படுத்தப்படும் மூன்று சூழ்நிலைகளைக் குறிப்பிடுக.
எடுத்துக்காட்டு 5.16
ஒரு முக்கோணத்தின் இரு பக்கங்களின் மையப்புள்ளிகளை இணைக்கும் கோட்டுத் துண்டானது, மூன்றாவது பக்கத்திற்கு இணையாகவும் மூன்றாவது பக்கத்தின் பாதியாகவும் இருக்கும் எனத் தொலைவு மற்றும் சாய்வு கருத்தைப் பயன்படுத்தி நிரூபிக்க.
தீர்வு
P (a, b) Q (c, d) மற்றும் R(e, f ) என்பன ஒரு முக்கோணத்தின் முனைப் புள்ளிகள் என்க.
PQ -யின் மையப்புள்ளி S மற்றும் PR-யின் மையப்புள்ளி T என்க

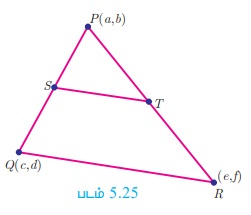
எனவே, ST ஆனது QR-க்கு இணை ஆகும். (ஏனெனில், இவற்றின் சாய்வுகள் சமம்)
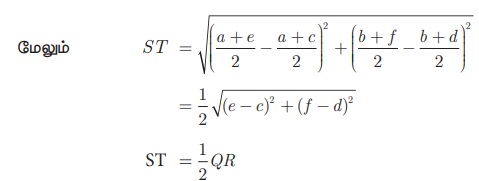
இதிலிருந்து, ST ஆனது QR -க்கு இணையாகவும் அதன் பாதியாகவும் இருக்கிறது.
குறிப்பு
வடிவியல் தேற்றத்தினை ஆயத்தொலை வடிவியல் மூலம் நிரூபிக்கலாம் என்பதற்கு மேற்கண்ட எடுத்துக்காட்டு ஓர் உதாரணம் ஆகும்.