Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ, Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я««Я»Ї, Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»Ї, Я«фЯ«»Я«┐Я«▒Я»ЇЯ«џЯ«┐ | Я«фЯ«ЋЯ»ЂЯ««Я»ЂЯ«▒Я»ѕ Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї | Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї - Я«ЄЯ«░Я»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«БЯ««Я»Ї | 11th Maths : UNIT 6 : Two Dimensional Analytical Geometry
11Я«хЯ«цЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 6 : Я«ЄЯ«░Я»ЂЯ«фЯ«░Я«┐Я««Я«ЙЯ«Б Я«фЯ«ЋЯ»ЂЯ««Я»ЂЯ«▒Я»ѕ Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї
Я«ЄЯ«░Я»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«БЯ««Я»Ї
Я«ЄЯ«░Я»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«БЯ««Я»Ї
(Angle between two straight lines)
Я«њЯ«░Я»Ђ Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«ЋЯ«хЯ»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«▒Я«┐Я«»Я»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«▒Я»ѕЯ«»Я»іЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ««Я»ЇЯ«фЯ«ЪЯ«┐Я«»Я»І Я«ЁЯ««Я»ѕЯ«»Я«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я»Ї Я«ЄЯ«░Я»Ђ Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЁЯ«цЯ«┐Я«▓Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї (acute angle) Я««Я«▒Я»ЇЯ«▒Я»іЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«хЯ«┐Я«░Я«┐Я«ЋЯ»ІЯ«БЯ««Я»Ї (obtuse angle) Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«џЯ««Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«░Я»Ђ Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я««Я«┐Я«ЋЯ»ѕ Я«еЯ«┐Я«░Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ (Я«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 180┬░) Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕЯ«»Я«┐Я«ЕЯ»ЇЯ«фЯ«ЪЯ«┐ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«БЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ»ѕ Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Є Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
1. Я«ЄЯ«БЯ»ѕ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕ (Condition for parallel lines)
Я«њЯ«ЕЯ»ЇЯ«▒Я»ѕЯ«»Я»іЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«│Я«ЙЯ««Я«▓Я»Ї, Я«њЯ«░Я»Є Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЄЯ«░Я»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
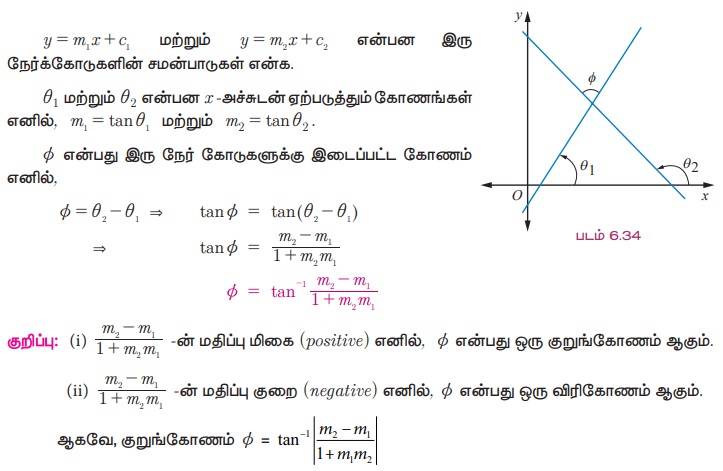
y = m1x + c1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y = m2x + c2
Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЄЯ«БЯ»ѕ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЄЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«БЯ««Я»Ї Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я««Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ ¤ђ.

Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«▓Я»ЇЯ«▓Я«ЙЯ«ц (non-vertical) Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«ЙЯ«»Я»ЇЯ«хЯ»ЂЯ«ЋЯ«│Я»Ї Я«џЯ««Я««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЁЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«▓Я»ЇЯ«▓Я«Й Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
a1x + b1y + c1 = 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї a2x + b2y + c2 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«ЪЯ«┐Я«хЯ««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕ

Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ: (i) ax + by + c = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«ЪЯ«┐Я«хЯ««Я»Ї ax + by = k
(ii) (x1, y1) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┤Я«┐Я«»Я«ЙЯ«Ћ, ax + by + c = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ ax + by = ax1 + by1 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
2. Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕ (Condition for perpendicular lines)

Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, a1x + b1y + c1 = 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї a2x + b2y + c2 = 0 Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«ЪЯ«┐Я«хЯ««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«хЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕ
a1 a2 + b1b2 = 0
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ: (i) ax + by + c = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«хЯ«ЪЯ«┐Я«хЯ««Я»Ї bx - ay = k
(ii) (x1, y1) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┤Я«┐Я«»Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї ax + by + c = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЅЯ«ЪЯ»ѕЯ«» Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ, bx - ay = bx1 РђЊ ay1 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.

Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
m1 m2 = -1 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЄЯ«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЄЯ«цЯ«ЕЯ»Ї Я««Я«▒Я»ЂЯ«цЯ«▓Я»ѕ Я««Я»єЯ«»Я»ЇЯ«»Я«ЙЯ«ЋЯ«ЙЯ«цЯ»Ђ. Я«ЈЯ«ЕЯ»єЯ«ЕЯ«┐Я«▓Я»Ї, Я«єЯ«» Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Е Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«ЕЯ«хЯ»ѕ, Я«јЯ«ЕЯ«┐Я«ЕЯ»ЂЯ««Я»Ї m1 m2 = -1 -Я«љ Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я«ЄЯ«»Я«▓Я«ЙЯ«цЯ»Ђ.
3. Я«њЯ«░Я»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«фЯ»Ї Я«фЯ»іЯ«▒Я»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«┐Я«▓Я»ѕ (Position of a point with respect to a straight line)
ax + by + c = 0 (c РЅа 0) Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«еЯ»ЇЯ«ц Я«њЯ«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«цЯ«│Я«цЯ»ЇЯ«цЯ»ѕ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«ЋЯ«│Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«┐Я«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
(i) Я«њЯ«░Я»Ђ Я«фЯ«ЋЯ»ЂЯ«цЯ«┐ Я«єЯ«цЯ«┐Я«»Я»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«цЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«ЁЯ«цЯ«ЕЯ»ѕ Я«њЯ«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«єЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї
(ii) Я««Я«▒Я»ЇЯ«▒Я«хЯ»ѕ Я«єЯ«цЯ«┐Я«»Я»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«цЯ»Ђ Я«ЁЯ«▓Я»ЇЯ«▓ Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЁЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я»ѕ Я«єЯ«цЯ«┐ Я«ЁЯ«▓Я»ЇЯ«▓Я«ЙЯ«ц Я«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ P(x1, y1) Я«єЯ«ЕЯ«цЯ»Ђ ax + by + c = 0, (c РЅа 0), Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«єЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«ЋЯ«хЯ»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«єЯ«цЯ«┐ Я«ЁЯ«▓Я»ЇЯ«▓Я«ЙЯ«ц Я«фЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»І Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї ax1 + by1 + c Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї c Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є Я«њЯ«░Я»Є Я«ЋЯ»ЂЯ«▒Я«┐ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«јЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ«ЎЯ»ЇЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї.
c > 0 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, P(x1, y1) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ ax + by + c = 0, Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«єЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«єЯ«цЯ«┐ Я«ЁЯ«▓Я»ЇЯ«▓Я«ЙЯ«ц Я«фЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, ax1 + by1 + c Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є Я«њЯ«░Я»Ђ Я««Я«┐Я«ЋЯ»ѕ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕ Я«єЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ: a1x + b1y + c1 = 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї a2x + b2y + c2 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї c1 > 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї c2 > 0 Я«јЯ«Е Я««Я«ЙЯ«▒Я»ЇЯ«▒Я«┐ Я«ЁЯ««Я»ѕЯ«цЯ»ЇЯ«цЯ«фЯ«┐Я«ЕЯ»Ї,
(i) a1a2 + b1b2 < 0 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЄЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«БЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(ii) a1a2 + b1b2 > 0 Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЄЯ«хЯ»ѕЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«БЯ««Я»Ї Я«њЯ«░Я»Ђ Я«хЯ«┐Я«░Я«┐Я«ЋЯ»ІЯ«БЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
4. Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ Я«хЯ«ЙЯ«»Я»ЇЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї (Distance Formulae)
Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│
(i) Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ
(ii) Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ
(iii) Я«ЄЯ«░Я»Ђ Я«ЄЯ«БЯ»ѕ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ
Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«џЯ»Ї Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я«цЯ»ЇЯ«цЯ»ѕ (Я«хЯ«ЙЯ«»Я»ЇЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕ) Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.

Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї
AB Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«ЪЯ»Ђ ax + by + c = 0 Я«јЯ«ЕЯ»ЇЯ«Ћ. (6.20)
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ P(x1, y1) Я«хЯ«┤Я«┐Я«»Я«ЙЯ«Ћ AB Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Ћ CD Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«хЯ«░Я»ѕЯ«Ћ. Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ P(x1, y1) -Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ AB-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«Ћ. Я«ЁЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ AB -Я«љ M -Я«▓Я»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«єЯ«цЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ AB -Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«Ћ. Я«ЁЯ«цЯ»Ђ AB -Я«љ R-Я«▓Я»ЂЯ««Я»Ї, CD -Я«љ Q -Я«▓Я»ЂЯ««Я»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
РѕаBOR = ╬▒ Я«јЯ«ЕЯ»ЇЯ«Ћ.
Я«ЄЯ«цЯ«ЕЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«хЯ«ЪЯ«┐Я«хЯ««Я»Ї
x cos ╬▒ + y sin ╬▒ = p, (p = OR) (6.21)
Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї (6.20) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (6.21), Я«њЯ«░Я»Є Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«јЯ«ЕЯ«хЯ»Є, Я«њЯ«цЯ»ЇЯ«ц Я«ЋЯ»ЂЯ«БЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ««Я«хЯ«┐Я«ЋЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
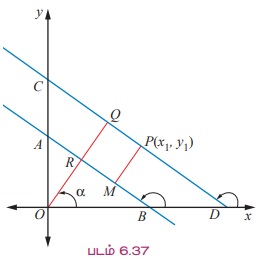

Я«ЋЯ»ІЯ«ЪЯ»Ђ CD -Я«ЕЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«хЯ«ЪЯ«┐Я«хЯ««Я»Ї.
x cos ╬▒ + y sin ╬▒ = p', (p' = OQ) (6.21)
Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ P (x1, y1,) Я«хЯ«┤Я«┐Я«»Я»Є Я«џЯ»єЯ«▓Я»ЇЯ«хЯ«цЯ«ЙЯ«▓Я»Ї
РЄњ p' = x1 cos ╬▒ + y1 sin ╬▒ (6.22)
P Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐, Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ AB -Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«єЯ«цЯ«┐Я«»Я»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«» Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«єЯ«цЯ«┐Я«»Я»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ц Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»І Я«ЁЯ««Я»ѕЯ«»Я«▓Я«ЙЯ««Я»Ї. Я«єЯ«цЯ«▓Я«ЙЯ«▓Я»Ї,
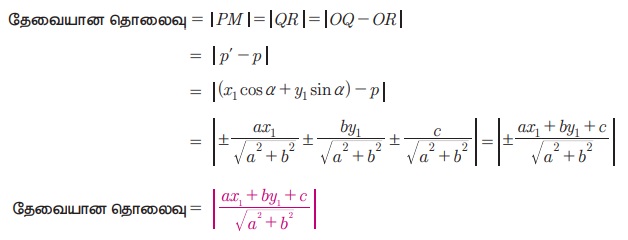
(iii) a1x + b1y + c1 = 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї a1x + b1y + c2 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЄЯ«░Я»Ђ Я«ЄЯ«БЯ»ѕ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ,
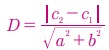
(Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ (x1, y1) Я«фЯ«цЯ«┐Я«▓Я«ЙЯ«Ћ Я«єЯ«цЯ«┐Я«»Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я««Я»ЂЯ«ЕЯ»ЇЯ«фЯ»Ђ Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї Я«џЯ»єЯ«»Я»ЇЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ѕЯ«фЯ»Ї Я«фЯ»ІЯ«▓Я»Ї Я«ЄЯ«еЯ»ЇЯ«цЯ«џЯ»Ї Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я«цЯ»ЇЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«Ћ Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї)
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ:
Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«џЯ«┐Я«▓ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»Ї
Рђб P(x1, y1) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ, ax + by + c = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Q -Я«ЕЯ»Ї Я«єЯ«»Я«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»ЂЯ«ЋЯ«│Я»ѕ, (Я«цЯ»ЂЯ«БЯ»ѕЯ«»Я«▓Я«ЋЯ»Ђ Я«хЯ«ЪЯ«┐Я«хЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц)

Рђб P(x1, y1) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«ЕЯ»Ї ax + by + c = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«фЯ»Ї 6.38 Я«фЯ»іЯ«▒Я»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«фЯ»Ї Я«фЯ«┐Я««Я»ЇЯ«фЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ ![]() -Я«ЕЯ»Ї Я«єЯ«»Я«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»ЂЯ«ЋЯ«│Я»ѕ,
-Я«ЕЯ»Ї Я«єЯ«»Я«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»ЂЯ«ЋЯ«│Я»ѕ,
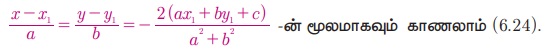
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.22 3x + 4y = 7 Я«јЯ«ЕЯ»ЇЯ«▒ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ (1, 2) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┤Я«┐Я«»Я»Є Я«џЯ»єЯ«▓Я»ЇЯ«▓Я«ЋЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ«┐Я«» Я«ЄЯ«БЯ»ѕ Я«ЋЯ»ІЯ«ЪЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
3x + 4y = 7 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Е Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
3x + 4y = 3x1 + 4y1
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ (x1, y1) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ (1, 2) Я«јЯ«ЕЯ»ЇЯ«Ћ.
РЄњ 3x + 4y = 3(1) + 4(2)
3x + 4y = 11
Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, 3x + 4y = 7 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
4x - 3y = 4x1 - 3y1
Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ«БЯ»ЇЯ«Ъ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ (x1, y1) = (1, 2) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┤Я«┐Я«»Я»Є Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«јЯ«ЕЯ«┐Я«▓Я»Ї
РЄњ 4x - 3y = 4(1) + 3(2)
4x - 3y = -2
Я«јЯ«ЕЯ«хЯ»Є Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є
3x + 4y = 11
4x - 3y = -2 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.23 Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
(i) (5,4) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (2,0) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»ѓЯ«░Я««Я»Ї
(ii) 5x + 12y РђЊ 3 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї (1,2) Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»ѓЯ«░Я««Я»Ї.
(iii) 3x + 4y = 12 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 6x + 8y + 1 = 0 Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»ѓЯ«░Я««Я»Ї.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
(i) (x1, y1) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (x2, y2) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ (5, 4) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (2, 0) Я«јЯ«ЕЯ»ЇЯ«Ћ.
Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ»ѓЯ«░Я««Я»Ї
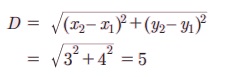
(ii) ax + by + c = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї (x1, y1) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»ѓЯ«░Я««Я»Ї
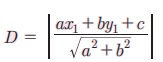
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, 5x + 12y РђЊ 3 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї (1 , 2) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»ѓЯ«░Я««Я»Ї
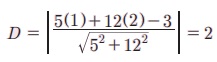
(iii) a1x + b1y + c1 = 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї a1x + b1y + c2 = 0 Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»ѓЯ«░Я««Я»Ї
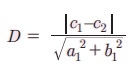
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕ 3x + 4y - 12 = 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 3x + 4y + 1/2 = 0 Я«јЯ«Е Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ, a1 = 3, b1 = 4, c1 = -12, c2, = 1/2
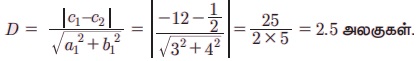
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.24 Я«єЯ«цЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 2x + y = 5 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ Я««Я«┐Я«Ћ Я«ЁЯ«БЯ»ЇЯ««Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«єЯ«цЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 2x + y = 5 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»Є Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«єЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┤Я«┐Я«»Я»Є Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ x РђЊ 2y = 0.
2x + y = 5, x РђЊ 2y = 0 Я«ЄЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»ЂЯ«ЋЯ«│Я»Ї x = 2, y = 1 Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ, Я«єЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«░Я»ЂЯ«ЋЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ (2, 1) Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я««Я«ЙЯ«▒Я»ЇЯ«▒Я»Ђ Я««Я»ЂЯ«▒Я»ѕ
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ (6.23) Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц,
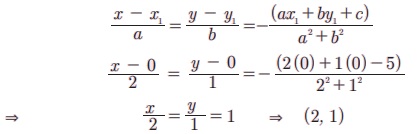
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.25 3x + 4y + 2 = 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 5x + 12y - 5 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЄЯ«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЄЯ«░Я»ЂЯ«џЯ««Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї 3x + 4y + 2 = 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 5x + 12y - 5 = 0
Я««Я»ЂЯ«цЯ«▓Я«┐Я«▓Я»Ї, Я«ЄЯ«░Я»Ђ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«»Я»ѕ Я««Я«┐Я«ЋЯ»ѕЯ«»Я«ЙЯ«Ћ Я««Я«ЙЯ«▒Я»ЇЯ«▒,
3x + 4y + 2 = 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї -5x -12y + 5 = 0 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЄЯ«░Я»Ђ Я«џЯ««Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ,
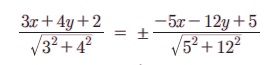
(Я«еЯ«ЋЯ«░Я»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«џЯ««Я«цЯ»ѓЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї)
a1a1 + b1b1 = -15 РђЊ 48 < 0, Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї
Я«ЄЯ«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ЂЯ«▒Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЄЯ«░Я»Ђ Я«џЯ««Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ,
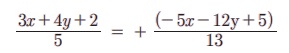
РЄњ 64 x + 112y + 1 = 0
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.26 x + y = 5 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї 4x + 3y -12 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 2 Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
x + y = 5 -Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«јЯ«еЯ»ЇЯ«ц Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ЂЯ««Я»Ї x = t, y = 5- t Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(t, 5 - t) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 4x + 3y -12 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ 2 Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї,
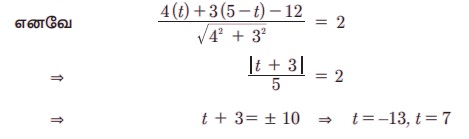
Я«јЯ«ЕЯ«хЯ»Є Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»Ї (-13, 18) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (7, -2)
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.27 Я«њЯ«░Я»Ђ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«Е Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ A(6, 8) Я«хЯ«┤Я«┐Я«»Я»Є Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ЄЯ«▓Я»Ї, Я«єЯ«цЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«┐Я«»Я««Я«фЯ»ЇЯ«фЯ«ЙЯ«цЯ»ѕЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
(x1, y1) = (6, 8) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«єЯ«цЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ (O-Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ) Я«ЁЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«┐Я«»Я««Я«фЯ»ЇЯ«фЯ«ЙЯ«цЯ»ѕЯ«»Я«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ P(h,k) Я«јЯ«ЕЯ»ЇЯ«Ћ.
Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«Е Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ A (6, 8) -Я«ЕЯ»Ї Я«хЯ«┤Я«┐Я«»Я»Є, m Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ«ЙЯ«»Я»ЇЯ«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
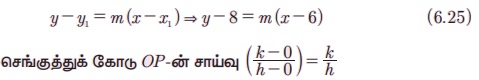
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ OP Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ (6.25) -Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
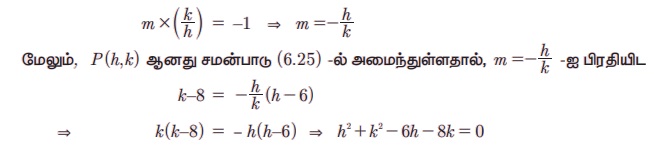
P(h,k) -Я«ЕЯ»Ї Я«еЯ«┐Я«»Я««Я«фЯ»ЇЯ«фЯ«ЙЯ«цЯ»ѕ
x2 + y2 РђЊ 6x - 8y = 0
Я«њЯ«░Я»Ђ Я«ЁЯ«░Я»ѕ Я«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЅЯ«│Я»ЇЯ«│Я««Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«БЯ««Я»Ї, Я«њЯ«░Я»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЅЯ«БЯ»ЇЯ««Я»ѕ Я«ЄЯ«цЯ«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«ЁЯ«▒Я«┐Я«»Я«▓Я«ЙЯ««Я»Ї.
5. Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ (Family of Lines)
Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«»Я»ѕ Я«еЯ«┐Я«▒Я»ѕЯ«хЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«»Я»ЂЯ««Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«фЯ«┐Я«ЕЯ»ЇЯ«фЯ«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«јЯ«▓Я»ЇЯ«▓Я«Й Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї, Я«њЯ«░Я»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЋЯ»ђЯ«┤Я»Є Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«џЯ«┐Я«▓ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ m, k Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї h Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«ЋЯ«│Я»Ї
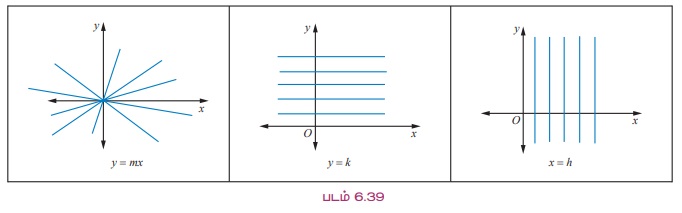
ax + by + c = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«ЪЯ«┐Я«хЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї a, b Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї c Я«јЯ«Е Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«ЋЯ«│Я»Ї Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«ЋЯ«цЯ»Ї Я«цЯ»ІЯ«ЕЯ»ЇЯ«▒Я»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЅЯ«БЯ»ЇЯ««Я»ѕ Я«ЁЯ«цЯ»ЂЯ«хЯ«▓Я»ЇЯ«▓. Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ b Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«Ћ (Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ a, Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я»Ї Я«јЯ«цЯ»Ђ Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я««Я«▒Я»ЇЯ«▒Я«цЯ«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»І Я«ЁЯ«цЯ»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«Ћ),

Я««Я»ЄЯ«▓Я»Є Я«ЋЯ«БЯ»ЇЯ«Ъ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«џЯ»Ї Я«џЯ«ЙЯ«»Я»ЇЯ«хЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я«јЯ«┤Я»ЂЯ«ц Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«ЋЯ«│Я»ѕ Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї, Я«ЁЯ«еЯ»ЇЯ«ц Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я»ѕ Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я»ѕЯ«ЋЯ»ЇЯ«Ћ Я«ЄЯ«»Я«▓Я«ЙЯ«цЯ»Ђ Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї, Я«цЯ»єЯ«│Я«┐Я«хЯ«ЙЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї, Я«јЯ«▓Я»ЇЯ«▓Я«Й Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«ЋЯ«│Я»ѕ Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»Ї Я«хЯ«┐Я«│Я»ѕЯ«хЯ«ЙЯ«Ћ Я«њЯ«░Я»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«цЯ»ђЯ«░Я»ЇЯ««Я«ЙЯ«ЕЯ«┐Я«ЋЯ»ЇЯ«Ћ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«ЋЯ«│Я»Ї Я«цЯ»ЄЯ«хЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«┐Я«░Я«цЯ«┐Я«»Я«┐Я«ЪЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«њЯ«░Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ Я««Я«▒Я»ЇЯ«▒ Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«»Я»ѕЯ«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ««Я«ЙЯ«ЕЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, Я«њЯ«░Я»Ђ Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«»Я»ѕ Я«еЯ«┐Я«▒Я»ѕЯ«хЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«њЯ«░Я»Ђ Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«»Я»ѕ Я«фЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ»ЇЯ«цЯ«ЋЯ»ѕЯ«» Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«њЯ«▒Я»ЇЯ«▒Я»ѕЯ«цЯ»Ї Я«цЯ»ЂЯ«БЯ»ѕЯ«»Я«▓Я«ЋЯ»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ (one parameter family of lines) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, Я«ЁЯ«еЯ»ЇЯ«ц Я«цЯ»єЯ«░Я«┐Я«»Я«ЙЯ«ц Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«»Я«ЙЯ«ЕЯ«цЯ»Ђ Я«цЯ»ЂЯ«БЯ»ѕЯ«»Я«▓Я«ЋЯ»Ђ (Parameter) Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
y = mx + b Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«хЯ«ЋЯ»ѕЯ«ЋЯ«│Я»ѕ Я«еЯ«ЙЯ««Я»Ї Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«┐Я«хЯ«ЙЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї. Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«ЋЯ»ѕЯ«ЋЯ«│Я»Ї Я«њЯ«▒Я»ЇЯ«▒Я»ѕЯ«цЯ»Ї Я«цЯ»ЂЯ«БЯ»ѕЯ«»Я«▓Я«ЋЯ»Ђ Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї (one parameter family of lines) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«хЯ«цЯ»Ђ Я«хЯ«ЋЯ»ѕ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«цЯ»ЂЯ«БЯ»ѕЯ«»Я«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї (two parameters family of lines).
(i) m Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«Е Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐.
(ii) b Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї m Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«Е Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐.
(iii) m Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«░Я«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«ЋЯ«│Я»Ї.
6. Я«њЯ«░Я»Ђ Я«цЯ»ЂЯ«БЯ»ѕЯ«»Я«▓Я«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї (One Parameter families)
(i) m Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«Е Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ Я«јЯ«ЕЯ»ЇЯ«Ћ.
y = mx + b Я«јЯ«ЕЯ»ЇЯ«▒ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї b = 5 Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ m Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я««Я»єЯ«»Я»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї, 5 Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЅЯ«ЪЯ»ѕЯ«» y- Я«ЁЯ«џЯ»ЇЯ«џЯ»Ђ Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ.
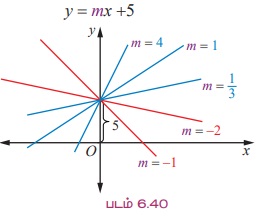
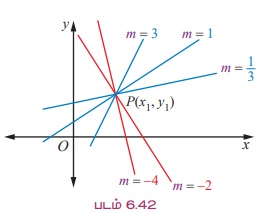
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ m - Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї - 1, -2, 1/3, 1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 4 Я«јЯ«Е Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ, Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«џЯ«┐Я«▓ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї (Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕ) Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.28 y = mx + 2 Я«јЯ«ЕЯ»ЇЯ«▒ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї, 2x + 3y = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«ЕЯ»Ї x -Я«ЕЯ»Ї Я«єЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ«ЙЯ«»Я»ЇЯ«хЯ»Ђ m Я«єЯ«ЋЯ«┐Я«»Я«Е Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«еЯ»ЇЯ«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
y = mx + 2 Я«јЯ«ЕЯ»ЇЯ«▒ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«Б, Я«цЯ»ЂЯ«БЯ»ѕЯ«»Я«▓Я«ЋЯ»Ђ m -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«Б Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.
y = mx + 2 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 2x + 3y = 10 Я«єЯ«ЋЯ«┐Я«» Я«ЄЯ«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐
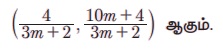
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ, Я«џЯ«ЙЯ«»Я»ЇЯ«хЯ»Ђ m Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї x-Я«ЕЯ»Ї Я«єЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«▒Я»ЂЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«┤Я»ЂЯ«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«Е Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«Е.
Я«јЯ«ЕЯ«хЯ»Є x-Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ 4/3m+2 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
РЄњ 3m+2 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ 4 -Я«љ Я«хЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.
(Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, ┬▒1, ┬▒2 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ┬▒4)
Я«јЯ«ЕЯ«хЯ»Є 3m + 2 = ┬▒1, 3m + 2 = ┬▒2, 3m + 2 = ┬▒4
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ m Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»Ї, Я««Я»ЄЯ«▓Я»ЂЯ«│Я»ЇЯ«│ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї,
m = {-2, -1, 0} Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї y = - 2x + 2, y = x + 2 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y = 2 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(ii) b Я«њЯ«░Я»Ђ Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї m Я«њЯ«░Я»Ђ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«Е Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ Я«јЯ«ЕЯ»ЇЯ«Ћ.
m Я«јЯ«ЕЯ»ЇЯ«▒ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«Е Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«»Я»ѕ m = - 2 Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї y = mx + b Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ y = -2x + b Я«јЯ«Е Я««Я«ЙЯ«▒Я»ЇЯ«▒Я««Я«ЪЯ»ѕЯ«»Я»ЂЯ««Я»Ї. b - Я«ЕЯ»Ї Я«фЯ«▓Я»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я««Я»єЯ«»Я»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«ЙЯ«»Я»ЇЯ«хЯ»Ђ -2 Я«ЅЯ«│Я»ЇЯ«│ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї. Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я»Ї Я«џЯ«┐Я«▓Я«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»ѕЯ«фЯ»Ї Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї. Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, b -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ -3, -1, 0, 1, 2, 3 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 4 Я«јЯ«Е Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ, Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«џЯ«┐Я«▓ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ (Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕ) Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
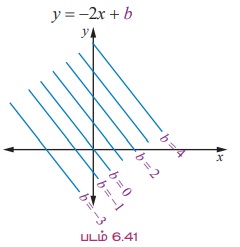
Я«ЄЯ«БЯ»ѕ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«єЯ«ЋЯ«┐Я«» Я«џЯ«┐Я«▒Я«фЯ»ЇЯ«фЯ»Ђ Я«хЯ«ЋЯ»ѕЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ : ax + by + c = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ ax + by + ╬╗ = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
╬╗ (lambda)-Я«ЕЯ»Ї Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ ax + by + c = 0 - Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Е Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї.
Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ : ax + by + c = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ bx РђЊ ay + ╬╗ = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
╬╗ -Я«ЕЯ»Ї Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ ax + by + c = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«Е Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї.
7. Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«цЯ»ЂЯ«БЯ»ѕЯ«»Я«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ (Two parameters families)
(iii) m Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«ЋЯ«│Я»Ї Я«јЯ«ЕЯ»ЇЯ«Ћ.
y = mx + b -Я«▓Я»Ї m Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ Я««Я«ЙЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»ЇЯ«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«хЯ«░Я»ѕЯ«фЯ«ЪЯ«цЯ»ЇЯ«цЯ»ѕ Я«јЯ«│Я«┐Я«цЯ«┐Я«▓Я»Ї Я«хЯ«░Я»ѕЯ«» Я«ЄЯ«»Я«▓Я«ЙЯ«цЯ»Ђ. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї, m -Я«ЕЯ»Ї Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я««Я»єЯ«»Я»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ y - y1 = m (x РђЊ x1) Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«хЯ«░Я»ѕЯ«фЯ«ЪЯ«цЯ»ЇЯ«цЯ»ѕ Я«хЯ«░Я»ѕЯ«» Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї. Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, x = x1 Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«цЯ»Ї Я«цЯ«хЯ«┐Я«░ (x1, y1) Я«јЯ«ЕЯ»ЇЯ«▒ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«Е Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┤Я«┐Я«џЯ»ЇЯ«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї -2, -4, 7, 1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 3 Я«єЯ«ЋЯ«┐Я«» m-Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«» Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
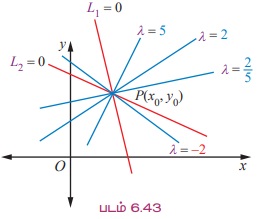
8. Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┤Я«┐Я«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
L1 = a1x + b1y + c1 = 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї L2 = a2x + b2y + c2 = 0 Я«єЯ«ЋЯ«┐Я«» Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┤Я«┐Я«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
L1 + ╬╗ L2 = 0 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(a1x + b1y + c1) + ╬╗ (a2x + b2y + c2) = 0
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ ╬╗ (lambda) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ»ЂЯ«БЯ»ѕЯ«»Я«▓Я«ЋЯ»Ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ ╬╗-Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.29 3x + 2y + 5 = 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 3x РђЊ 4y + 6 = 0 Я«єЯ«ЋЯ«┐Я«» Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┤Я«┐Я«»Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї (1, 1) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┤Я«┐Я«»Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┤Я«┐Я«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
(a1x + b1y + c1) + ╬╗ (a2x + b2y + c2) = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є, (3x + 2y + 5) + (3x РђЊ 4y + 6) = 0
Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«ЕЯ«ЋЯ»ІЯ«ЪЯ»Ђ (1, 1) Я«хЯ«┤Я«┐ Я«џЯ»єЯ«▓Я»ЇЯ«хЯ«цЯ«ЙЯ«▓Я»Ї, Я««Я»ЄЯ«▓Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«еЯ«┐Я«▒Я»ѕЯ«хЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«»Я»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є, {3+ 2 (1) + 5} + ╬╗ {3(1) - 4(1) + 6} = 0 РЄњ ╬╗ = -2
РЄњ ╬╗ = -2 -Я«љ Я««Я»ЄЯ«▓Я»ЂЯ«│Я»ЇЯ«│ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«фЯ«┐Я«░Я«цЯ«┐Я«»Я«┐Я«ЪЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ,
3x - 10y +7 = 0
(Я«ЄЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«ЪЯ«┐Я«хЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«ЄЯ«ЋЯ»ЇЯ«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ѕЯ«џЯ»Ї Я«џЯ«░Я«┐Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ)
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.30 A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B Я«єЯ«ЋЯ«┐Я«» Я«ЄЯ«░Я»Ђ Я«ЋЯ«┐Я«░Я«ЙЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«┐Я«▒Я«фЯ»ЇЯ«фЯ«ЙЯ«Е Я««Я«┐Я«ЕЯ»ЇЯ«џЯ«ЙЯ«░Я««Я»Ї Я«ЁЯ«│Я«┐Я«ЋЯ»ЇЯ«Ћ Я«њЯ«░Я»Ђ Я«цЯ»ЂЯ«БЯ»ѕ Я««Я«┐Я«ЕЯ»ЇЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ»ѕ l Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ«ЙЯ«▓Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«Ћ Я«ЁЯ«░Я«џЯ»Ђ Я«цЯ«┐Я«ЪЯ»ЇЯ«ЪЯ««Я«┐Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ. A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B -Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є l Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ«ЙЯ«▓Я»ѕЯ«»Я«┐Я«▓Я»Ї P Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Q Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«ЪЯ«┐Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є 3 Я«ЋЯ«┐Я««Я»ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 5 Я«ЋЯ«┐Я««Я»ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї. P Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Q -Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»ЄЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«цЯ»ѓЯ«░Я««Я»Ї 6 Я«ЋЯ«┐Я««Я»ђ Я«јЯ«ЕЯ«┐Я«▓Я»Ї,
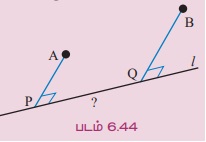
(i) Я«ЄЯ«░Я»Ђ Я«ЋЯ«┐Я«░Я«ЙЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ»ЂЯ«БЯ»ѕ Я««Я«┐Я«ЕЯ»ЇЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ»ЂЯ«ЪЯ«ЕЯ»Ї Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ««Я»ЇЯ«фЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я««Я«┐Я«ЋЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я»ѕЯ«еЯ»ЇЯ«ц Я«еЯ»ђЯ«│Я««Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. (Я«ЋЯ«┐Я«░Я«ЙЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«цЯ»ЂЯ«БЯ»ѕ Я««Я«┐Я«ЕЯ»Ї Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«џЯ«ЙЯ«▓Я»ѕЯ«ЋЯ«│Я»Ї) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї
(ii) Я««Я«┐Я«ЕЯ»Ї Я«ЋЯ««Я»ЇЯ«фЯ«┐ Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї Я«фЯ«ЙЯ«цЯ»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«фЯ«┐Я«░Я«цЯ«┐Я«фЯ«▓Я«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ«цЯ»ЇЯ«цЯ»ЂЯ«хЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ«▓Я»Ї:
PQ-Я«љ Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕ x -Я«ЁЯ«џЯ»ЇЯ«џЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї,
PA-Я«љ Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕ y-Я«ЁЯ«џЯ»ЇЯ«џЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї,
P -Я«љ Я«єЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«Ћ.
Я«јЯ«ЕЯ«хЯ»Є, P(0, 0), A(0, 3) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B(6, 5) Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
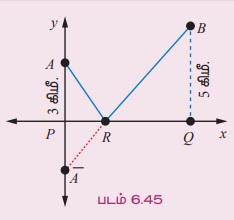

Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.31 Я«њЯ«░Я»Ђ Я««Я«ЋЯ«┐Я«┤Я»ЂЯ«еЯ»ЇЯ«цЯ«┐Я«▓Я»Ї, Я««Я»ЂЯ«цЯ«▓Я»Ї 1.8 Я«ЋЯ«┐Я««Я»ђ Я«хЯ«░Я»ѕ Я«фЯ«»Я«БЯ««Я»Ї Я«џЯ»єЯ«»Я»ЇЯ«» Я«хЯ«ЙЯ«ЪЯ«ЋЯ»ѕ Рѓ╣25 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▓Я»Ї Я«фЯ«»Я«БЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЋЯ«┐Я«▓Я»ІЯ««Я»ђЯ«ЪЯ»ЇЯ«ЪЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Рѓ╣12 Я«хЯ«ЙЯ«ЪЯ«ЋЯ»ѕ Я«хЯ«џЯ»ѓЯ«▓Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«фЯ«»Я«Б Я«цЯ»ѓЯ«░Я««Я»Ї x Я«ЋЯ«┐Я«▓Я»І Я««Я»ђЯ«ЪЯ»ЇЯ«ЪЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«хЯ«ЙЯ«ЪЯ«ЋЯ»ѕ Рѓ╣y-Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї 15 Я«ЋЯ«┐Я«▓Я»ІЯ««Я»ђЯ«ЪЯ»ЇЯ«ЪЯ«░Я»Ї Я«фЯ«»Я«БЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«хЯ«ЙЯ«ЪЯ«ЋЯ»ѕ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
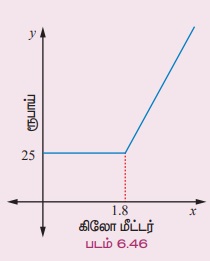
1.8 Я«ЋЯ«┐Я«▓Я»ІЯ««Я»ђЯ«ЪЯ»ЇЯ«ЪЯ«░Я»Ї Я«хЯ«░Я»ѕ Я««Я«ЙЯ«▒Я«ЙЯ«ц Я«хЯ«ЙЯ«ЪЯ«ЋЯ»ѕ Рѓ╣25. Я«јЯ«ЕЯ«хЯ»Є, Я«ЁЯ«цЯ«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ y = 25, 0 РЅц x РЅц 1.8 (6.26)
Я«ЋЯ«┐Я«▓Я»ІЯ««Я»ђЯ«ЪЯ»ЇЯ«ЪЯ«░Я»Ї 1.8-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▓Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЋЯ«┐Я«▓Я»ІЯ««Я»ђЯ«ЪЯ»ЇЯ«ЪЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«хЯ«ЙЯ«ЪЯ«ЋЯ»ѕ Рѓ╣12. Я«ЄЯ«цЯ«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ,
y = 25 + 12 (x - 1.8), x > 1.8 (6.27)
Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї (6.26) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (6.27) Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ,
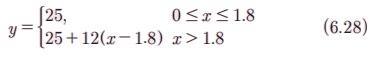
x = 15 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ (6.27) -Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ
y = 25 + 12 (15 - 1.8) = 183.40.
Я«Ѓ. 15 Я«ЋЯ«┐Я««Я»ђ Я«фЯ«»Я«БЯ««Я»Ї Я«џЯ»єЯ«»Я»ЇЯ«» Я«хЯ«ЙЯ«ЪЯ«ЋЯ»ѕ Рѓ╣183.40.
Я«еЯ»ђЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«хЯ«ЙЯ«ЪЯ«ЋЯ»ѕ Я««Я«ЋЯ«┐Я«┤Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«џЯ»ЄЯ«хЯ»ѕ (call taxi) Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї, Я«ЅЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЋЯ»ѕЯ«фЯ»ЄЯ«џЯ«┐ Я««Я»ѓЯ«▓Я««Я»Ї Я«хЯ«ЙЯ«ЪЯ«ЋЯ»ѕ Я««Я«ЋЯ«┐Я«┤Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«▒Я«┐Я«ЕЯ»ѕ Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ, Я«ЅЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЁЯ«┤Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ Я«цЯ«ЙЯ«ЕЯ«ЙЯ«ЋЯ«хЯ»Є Я«ЅЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«░Я»ЂЯ«ЋЯ«ЙЯ««Я»ѕЯ«»Я«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я««Я«ЋЯ«┐Я«┤Я»ЂЯ«еЯ»ЇЯ«цЯ»ЂЯ«ЪЯ«ЕЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ»іЯ«│Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«фЯ«┐Я«▒Я«ЋЯ»Ђ Я«цЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«хЯ«┐Я«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЄЯ«▒Я»ЇЯ«ф Я«еЯ»ђЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«хЯ«еЯ»ЇЯ«цЯ»Ђ Я«еЯ»ђЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ»єЯ«▓Я»ЇЯ«▓Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«» Я«ЄЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«цЯ«ЙЯ«ЕЯ«ЙЯ«ЋЯ«хЯ»Є Я«хЯ«┤Я«┐Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї. Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«еЯ»ђЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЁЯ«┤Я»ѕЯ«цЯ»ЇЯ«ц Я«ЄЯ«ЪЯ««Я»Ї, Я«џЯ»єЯ«▓Я»ЇЯ«▓Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«» Я«ЄЯ«ЪЯ««Я»Ї, Я«фЯ«ЙЯ«цЯ»ѕ, Я«цЯ»ѓЯ«░Я««Я»Ї... Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»іЯ«│Я»ЇЯ«│ Я«јЯ«хЯ»ЇЯ«хЯ«ЋЯ»ѕЯ«»Я«ЙЯ«Е Я«єЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ?
Я«ЄЯ«цЯ«ЕЯ»ѕ Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»іЯ«│Я»ЇЯ«│ : www.mapbox.com Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«▓Я»ѕЯ«цЯ«│Я«цЯ»ЇЯ«цЯ»ѕ Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«Ћ.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 6.32 (3, 0) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (5, 2) Я«єЯ«ЋЯ«┐Я«» Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕ Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕ (3, 0)-Я«љ Я««Я»ѕЯ«»Я««Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ 15┬░ Я«ЋЯ«ЪЯ«┐Я«ЋЯ«ЙЯ«░ Я«јЯ«цЯ«┐Я«░Я»ЇЯ«џЯ»ЂЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я»Ї Я«џЯ»ЂЯ«┤Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«фЯ»ЂЯ«цЯ«┐Я«» Я«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ

Я«фЯ»ЂЯ«цЯ«┐Я«» Я«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«џЯ«ЙЯ«»Я»ЇЯ«хЯ»Ђ = m = tan( 45┬░ + 15┬░)
= tan 60┬░ = Рѕџ3
Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ (3, 0) Я«хЯ«┤Я«┐Я«»Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«џЯ«ЙЯ«»Я»ЇЯ«хЯ»Ђ Рѕџ3 -Я«љЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ
y - 0 = Рѕџ3 (x - 3)
Рѕџ3x РђЊ y РђЊ 3Рѕџ3 = 0
Я«фЯ«»Я«┐Я«▒Я»ЇЯ«џЯ«┐ 6.3
1. 3x + 2y + 9 = 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 12x + 8y - 15 = 0 Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«Ћ.
2. 5x - 4y + 3 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Ћ, x -Я«ЁЯ«џЯ»ЇЯ«џЯ«┐Я«ЕЯ»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»Ђ 3 Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
3. 4x + 3y + 4 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (i) (-2, 4) (ii) (7, -3) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
4. (1, -1 ) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┤Я«┐Я«»Я»Є Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї
(i) x + 3y - 4 = 0-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Е
(ii) 3x + 4y = 6-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«Е,
Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
5. Я«џЯ«ЙЯ«»Я»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЕЯ»ѕ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ (-4, 7), Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї 5x РђЊ y + 7 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»Ђ Я«њЯ«░Я»Ђ Я««Я»ѓЯ«▓Я»ѕ Я«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я««Я«▒Я»ЇЯ«▒Я»іЯ«░Я»Ђ Я««Я»ѓЯ«▓Я»ѕЯ«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
6. 4x РђЊ y + 3 = 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 5x + 2y + 7 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┤Я«┐Я«»Я»Є Я«џЯ»єЯ«▓Я»ЇЯ«▓Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ«┐Я«»Я«цЯ»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї
(i) (-1, 2 ) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┤Я«┐Я«»Я»Є Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї
(ii) x - y + 5 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Е
(iii) x - 2y + 1 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«Е
Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
7. 12x + 5y + 2 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Ћ, (1, -1) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЁЯ«▓Я«ЋЯ»Ђ Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЄЯ«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
8. 3x + 4y - 6 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«Ћ, (2, 1) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 4 Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
9. 2x + 3y = 10 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Е Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«єЯ«» Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 15 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
10. (-10,- 2) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ x + y - 2 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я«цЯ»ЇЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
11. x sec ╬И + y cosec ╬И = 2a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї x cos ╬И - ysin ╬И = a cos 2 ╬И Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«єЯ«цЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ»Ї Я«цЯ»ѓЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є p1, Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї p2 Я«јЯ«ЕЯ«┐Я«▓Я»Ї p12 + p22? = a2 Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
12. Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«ЄЯ«БЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ»ѓЯ«░Я«цЯ»ЇЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
(i) 12x + 5y = 7 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 12 x + 5y + 7 = 0
(ii) 3 x РђЊ 4 y + 5 = 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 6x - 8 y - 15 = 0
13. 3x + 4y - 12 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ
(i) Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«Е (ii) Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Е Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
14. A(2, 0) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B(3, 1) Я«єЯ«ЋЯ«┐Я«» Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕ Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕ, Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ A -Я«љ Я«фЯ»іЯ«▒Я»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ«ЪЯ«┐Я«ЋЯ«ЙЯ«░ Я«јЯ«цЯ«┐Я«░Я»ЇЯ«цЯ«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї 15┬░ Я«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«џЯ»ЂЯ«┤Я«▒Я»ЇЯ«▒Я»ЂЯ«хЯ«цЯ«ЙЯ«▓Я»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«цЯ«┐Я«» Я«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
15. (1, 2) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«хЯ«░Я»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«њЯ«│Я«┐Я«ЋЯ»Ї Я«ЋЯ«цЯ«┐Я«░Я»Ї x- Я«ЁЯ«џЯ»ЇЯ«џЯ«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ A-Я«▓Я»Ї Я«фЯ«┐Я«░Я«цЯ«┐Я«фЯ«▓Я«┐Я«цЯ»ЇЯ«цЯ»Ђ, (5,3) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┤Я«┐Я«»Я»Є Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ A -Я«ЕЯ»Ї Я«єЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
16. 5x = y + 7 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«Ћ Я«хЯ«░Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«ЪЯ»Ђ Я«єЯ«» Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЪЯ«ЕЯ»Ї Я«ЈЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ 10 Я«џ. Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЁЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
17. x + 2y - 9 = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«фЯ»Ї Я«фЯ»іЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ»Ђ (-2 , 3) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«фЯ«┐Я««Я»ЇЯ«фЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
18. Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«ЋЯ»ѕЯ«фЯ»ЇЯ«фЯ«Ъ Я«еЯ«ЋЯ«▓Я«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї 10 Я«фЯ«┐Я«░Я«цЯ«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»Ђ Я«фЯ«┐Я«░Я«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ Рѓ╣1.50 Я«хЯ»ђЯ«цЯ««Я»Ї Я«хЯ«џЯ»ѓЯ«▓Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. 10 Я«фЯ«┐Я«░Я«цЯ«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▓Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я«фЯ«┐Я«░Я«цЯ«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Рѓ╣1 Я«хЯ»ђЯ«цЯ««Я»Ї Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ«БЯ««Я»Ї Я«хЯ«џЯ»ѓЯ«▓Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ«┐Я«░Я«цЯ«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я»ѕЯ«»Я»ЂЯ««Я»Ї, y Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«еЯ«ЋЯ«▓Я»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ«БЯ«цЯ»ЇЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«Ћ.
(i) x - Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ 0 Я««Я»ЂЯ«цЯ«▓Я»Ї 50 Я«еЯ«ЋЯ«▓Я»ЇЯ«ЋЯ«│Я»Ї Я«хЯ«░Я»ѕ Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ«БЯ«цЯ»ЇЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«хЯ«░Я»ѕЯ«фЯ«ЪЯ««Я»Ї Я«хЯ«░Я»ѕЯ«Ћ.
(ii) 40 Я«фЯ«┐Я«░Я«цЯ«┐Я«ЋЯ«│Я»Ї Я«јЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ«БЯ««Я»Ї Я«јЯ«хЯ»ЇЯ«хЯ«│Я«хЯ»Ђ?
19. y = 5x + b Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ b Я««Я«ЙЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 3x - 4y = 6 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЪЯ«ЕЯ»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«ЕЯ»Ї x -Я«єЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ Я««Я»ЂЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«еЯ»ЇЯ«ц Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я»ѕЯ«еЯ»ЇЯ«цЯ«фЯ«ЪЯ»ЇЯ«џЯ««Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
20. y = mx - 3 Я«јЯ«ЕЯ»ЇЯ«▒ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї x - y = 6 Я«јЯ«ЕЯ»ЇЯ«▒ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ««Я»Ї, Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«ЕЯ»Ї x -Я«ЕЯ»Ї Я«єЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ«ЙЯ«»Я»ЇЯ«хЯ»Ђ m Я«єЯ«ЋЯ«┐Я«»Я«Е Я««Я»ЂЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, y = mx - 3 -Я«ЕЯ»Ї Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.