இரட்டை நேர்க்கோடுகள்

இரட்டை நேர்க்கோடுகள் (Pair of Straight lines)

இரண்டு அல்லது அதற்கு மேற்பட்ட சமன்பாடுகளை ஒன்றாக இணைத்து உயர்படி உடைய சமன்பாடுகளாக விவரிக்க முடியும். x மற்றும் y -ல் உள்ள நேரிய சமன்பாடு ஒரு நேர்க்கோட்டைக் குறிக்கும் என்பதை நாம் அறிவோம். இரண்டு நேரிய சமன்பாடுகளின் பெருக்கற்பலன் ஒரு இரட்டை நேர்க்கோட்டைக் குறிக்கிறது. இரட்டை நேர்க்கோட்டை x மற்றும் y -ல் ஒரு இருபடிச் சமன்பாடாகக் காணலாம்.

L1 = a1x + b1y + c1 = 0 மற்றும் L1 = a2x + b2y + c2 = 0 என்பன இரு தனித்தனி நேர்க்கோடுகள் என்க. P(x1, y1) என்ற புள்ளி L1 -ன் மீது அமைந்துள்ளது எனில் L1 = 0 என்ற சமன்பாட்டை நிறைவு செய்கிறது.

இதேபோல், P(x1, y1) என்ற புள்ளி L2 -ன் மீது அமைந்துள்ளது எனில், L2 = 0 என்ற சமன்பாட்டை நிறைவு செய்கிறது.

P(x1, y1) புள்ளியானது L1 = 0 அல்லது L2 = 0 இவற்றில் ஏதேனும் ஒன்றில் அமைந்திருக்கிறது எனில், (L1) (L2) = 0 என்ற சமன்பாட்டை நிறைவு செய்கிறது. மேலும், வேறு எந்த புள்ளியும் L1 . L2 = 0 -ஐ நிறைவு செய்யாது. எனவே, L1 . L2 = 0 என்பது L1 = 0 மற்றும் L2 = 0 என்ற கோடுகளின் இரட்டை நேர்க்கோடுகளைக் குறிக்கிறது. 

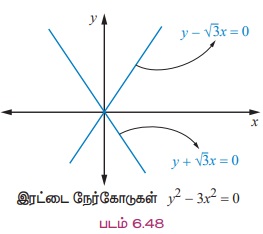
எடுத்துக்காட்டாக,

y + √3x = 0 மற்றும் y - √3x = 0. 

மேற்கண்ட இரண்டு சமன்பாடுகளும் ஆதி வழியே செல்லக்கூடியதாகும். இரண்டு நேர்க்கோடுகளின் சாய்வுகள் முறையே -√3 மற்றும் √3 எனக் குறிக்கிறது.

மேற்கண்ட சமன்பாடுகளின் சேர்ப்புச் சமன்பாடு

(y + √3x) (y - √3x) = 0. 

⇒ y2 - 3x2 = 0 என்பது ஒரு இரட்டை நேர்க்கோட்டைக் குறிக்கிறது. 

1. ஆதிவழியே செல்லும் இரட்டை நேர்க்கோடுகள் (Pair of lines passing through the origin)

நாம் முதலில் ஒரு எளிய வகை சமன்பாடுகளை எடுத்துக்கொள்ளலாம். இரு கோடுகள் ஆதி வழியே செல்லக்கூடியவை எனில், அவற்றின் சமன்பாடுகள்

y – m1x = 0 மற்றும் y – m2x = 0 என்க .

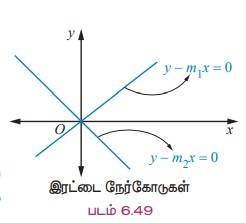
இவற்றின் ஒருங்கிணைந்த (சேர்ப்பு) சமன்பாடு

(y – m1x)( y – m2x) = 0  (6.29) 

y2 - (m1 + m2)xy + m1m2x2 = 0

மேலே உள்ள சமன்பாட்டை ax2 + 2hxy + by2 = 0 என்ற இரண்டாம் படி சமபடித்தான சமன்பாடாக எழுதலாம். இங்கு ஒவ்வொரு உறுப்பின் படியும் இரண்டாகும்.

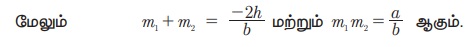
குறிப்பு: சமபடித்தான சமன்பாட்டின் கோடுகள் ஆதி வழிச் செல்லும்

எடுத்துக்காட்டு 6.33 5x2 + 6xy + y2 = 0 என்ற இரட்டை நேர்க்கோட்டின் தனித்தனிச் சமன்பாடுகளைக் காண்க.

தீர்வு

கொடுக்கப்பட்ட சமன்பாடு 5x2 + 6xy + y2 = 0 

மேற்கண்ட சமன்பாட்டை காரணிபடுத்த,

5 x2 + 5 xy + xy + y = 0

5x(x + y ) + y (x + y) = 0

(5x + y)(x + y) = 0 

எனவே, தேவையான கோடுகள், 5x + y = 0 , x + y = 0 

மாற்றுமுறை

கொடுக்கப்பட்டுள்ள சமன்பாடு சம படித்தான சமன்பாடு

5x2 + 6xy + y2 = 0

இருபுறமும் x2 ஆல் வகுக்க, 

மேற்கண்ட சமன்பாடானது

m2 + 6m + 5 = 0

காரணிபடுத்த கிடைப்பது,

(m + 1)( m + 5) = 0

⇒ m = -1, m = -5

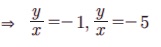
தேவையான சமன்பாடுகள் x + y = 0, 5x + y = 0

எடுத்துக்காட்டு 6.34 2x2 + 2xy + y2 = 0 என்ற சமன்பாட்டை இயலுமானால் இரட்டை நேர்க்கோட்டின் தனித்தனிச் சமன்பாடுகளாகப் பிரிக்கவும். 

தீர்வு 

2x2 + 2xy + y2 = 0 என்பது சமப்படித்தான சமன்பாடு எனவே, x2 ஆல் வகுத்து

y/m = m என பிரதியிட, m2 + 2 m + 2 = 0 எனக் கிடைக்கும். 

இங்கு m -ன் (சாய்வு) மதிப்பானது மெய்யெண் அல்ல (⸪ Δ = B2 – 4AC = 4 – 8 = -4 < 0) (கலப்பெண்) எனவே, 

2x2 + 2xy + y2 = 0 என்ற சமன்பாடுடைய எந்த நேர்க்கோடுகளும் அமையவில்லை. சில நேரங்களில் இந்த சமன்பாட்டை கற்பனைக் கோடுகள் எனக் கூறலாம். குறிப்பாக முழு தளத்திலும் (0, 0) மட்டுமே சமன்பாட்டை நிறைவு செய்கிறது.

2. இரட்டை நேர்க்கோடுகளுக்கு இடைப்பட்ட கோணம் (Angle between pair of straight lines) 

ஆதிவழிச் செல்லும் இரட்டை நேர்க்கோடுகளின் சமன்பாடு 

ax2 + 2hxy + by2 = 0    (6.30) 

m1 மற்றும் m2 என்பன இவ்விரு கோடுகளின் சாய்வுகள் என்க. 

சமன்பாடு (6.30) -ஐ x2 -ஆல் வகுத்து y/x = m என பிரதியிட,

bm2 + 2hm + a = 0 எனக் கிடைக்கும்.

இச்சமன்பாடு m -ல் இருபடி சமன்பாடாகும். 

இதன் மூலங்கள் m1 மற்றும் m2 எனில்

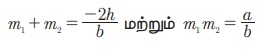
θ என்பது இவ்விரு கோடுகளுக்கு இடைப்பட்ட கோணம் எனில்,

சூத்திரத்திலிருந்து முடிவு செய்யக் கூடியவை

1. m1 மற்றும் m2 ஆகியவை மெய் மற்றும் வெவ்வேறானவை எனில் கோடுகள் மெய் மற்றும் வெவ்வேறானவைகளாகும், மேலும், h2 – ab > 0. 

2. m1 மற்றும் m2 ஆகியவை மெய் மற்றும் சமம் எனில் கோடுகள் மெய் மற்றும் ஒன்றியிருக்கும் (coincide), மேலும், h2 – ab = 0. 

3. m1 மற்றும் m2 ஆகியவை மெய் அல்ல எனில் கோடுகள் மெய்யல்ல (கற்பனை), மேலும், h2 – ab < 0.

ax2 + 2hxy + by2 = 0 -ஐ குறிக்கும் இரட்டைக் கோடுகள் ஆதி வழியே செல்கிறது. இக்கோடுகள் இரண்டும் இணை அல்லது ஒன்றியிருக்கும் எனில்,

tan θ = 0. அதாவது, h2 – ab = 0. மேலும், 

இக்கோடுகள் செங்குத்து எனில், cot θ = 0 .

⸫ a + b = 0 .

எடுத்துக்காட்டு 6.35 ax2 + 2hxy + by2 = 0 என்ற இரட்டை நேர்க்கோட்டிற்கு செங்குத்தாகவும், ஆதி வழிச் செல்லும் இரட்டைக் கோடுகளின் சமன்பாட்டைக் காண்க.

தீர்வு

m1 மற்றும் m2 என்பன ax2 + 2hxy + by2 = 0 என்ற கோடுகளின் சாய்வுகள் என்க. 

y – m1x = 0 மற்றும் y – m2x = 0    (6.31)

என்பன மேற்கண்ட சமன்பாட்டின் தனித்தனிச் சமன்பாடுகள் என்க. இவ்விரு சமன்பாடுகளின் சேர்ப்பு (ஒருங்கிணைந்த) சமன்பாடு

(y - m1x)(y - m2x) = 0 

y2 -( m1 + m2)xy + m1m2x2 = 0                     (6.32) 

கொடுக்கப்பட்டவை, ax2 + 2hxy + by2 = 0   (6.33) 

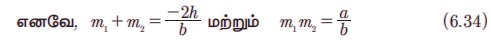
சமன்பாடு (6.31) -க்கு செங்குத்து கோடுகள்

இச்சமன்பாடுகளின் சேர்ப்பு சமன்பாடு,

(m1 y + x)(m2y + x) = 0

m1 m2y2 + (m1 + m2)xy + x2 = 0 

சமன்பாடு (6.34) -ஐ பயன்படுத்த,

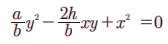
தேவையான சமன்பாடு ay2 - 2hxy + bx2 = 0     (6.35)

3. ax2 + 2hxy + by2 = 0 என்ற கோடுகளுக்கு இடைப்பட்ட கோணத்தின் இருசமவெட்டியின் சமன்பாடு காணுதல். (Equation of the angle bisectors of pair of straight lines)

y − m1x = 0 மற்றும் y − m2x = 0 

என்பன இரண்டு நேர்க்கோடுகளின் சமன்பாடு என்க.

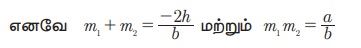
ஒரு புள்ளியிலிருந்து இரு கோடுகளுக்கு வரையப்படும் செங்குத்துக் கோடுகளின் நீளம் சமம் எனில், அப்புள்ளியின் நியமப்பாதை அக்கோடுகளுக்கு இடைப்பட்ட கோணத்தின் கோண இருசம் வெட்டி ஆகும்.

P(p,q) என்பது இரு சமவெட்டியின் நியமப்பாதையின் மீது அமைந்துள்ள ஏதேனும் ஒரு புள்ளி என்க.

y − m1x = 0 என்ற கோட்டிற்கு P(p,q) இருந்து வரையப்படும் செங்குத்துக் கோட்டின் நீளமானது y – m2x = 0 என்ற கோட்டிற்கு அப்புள்ளியிலிருந்து வரையப்படும் செங்குத்துக் கோட்டின் நீளத்திற்கு சமம்.

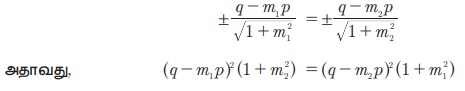
எளிதாக்குவதால்,

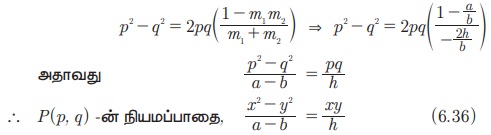
எடுத்துக்காட்டு 6.36 x2 – 4xy + y2 = 0 மற்றும் x + y = 3 ஆகிய நேர்க்கோடுகள் ஒரு சமப்பக்க முக்கோணத்தை அமைக்கும் எனக் காட்டுக.

தீர்வு

x + y = 3 என்ற கோடு x2 – 4xy + y2 = 0 என்ற இரட்டைக் கோட்டை A மற்றும் B-ல் வெட்டுகிறது என்க. மேலும் x2 – 4xy + y2 = 0 ஆதிபுள்ளியில் O வெட்டிக்கொள்ளும் 

x2 – 4xy + y2 = 0 என்ற கோடுகளுக்கு இடைப்பட்ட கோணம்.

x - y = 0 -ன் கோண இருசமவெட்டி கொடுக்கப்பட்ட கோடு AB, அதாவது x + y = 3 -க்கு செங்குத்தாக உள்ளது.

எனவே ΔAOB என்பது இரு சமப்பக்க முக்கோணம் ஆகும்.

⇒ ∠ABO = ∠BAO = 60°, மேலும் ∠AOB = 60°

எனவே, கொடுக்கப்பட்ட கோடுகள் ஒரு சமபக்க முக்கோணத்தை அமைக்கின்றது.

எடுத்துக்காட்டு 6.37 x2 – 2cxy – y2 = 0 மற்றும் x2 – 2dxy – y2 = 0 ஆகியவை இரட்டைக் கோடுகளை குறிக்கின்றன. ஒவ்வொரு இரட்டைக்கோடுகள் மற்ற இரட்டைக்கோடுகளுக்கு இடையே உள்ள கோணத்தை சமமாகப் பிரிக்கிறது எனில், cd = -1 என நிறுவுக.

தீர்வு 

கொடுக்கப்பட்ட இரட்டைக் கோடுகளின் சமன்பாடு 

x2 - 2cxy – y2 = 0    (6.37) 

x2 – 2dxy – y2 = 0   (6.38) 

சமன்பாடு (6.37) -ன் கோண இரு சமவெட்டிகளின் சமன்பாடு

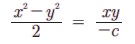
cx2 + 2xy – cy2 = 0       (6.39) 

சமன்பாடு (6.38) சமன்பாடு (6.37)-ன் கோண இருசமவெட்டி என்பதால் சமன்பாடு (6.38) மற்றும் (6.39)

x2 – 2dxy – y2 = 0

cx2 + 2xy – cy2 = 0 

ஒரே சமன்பாடாக அமைகிறது. 

எனவே, மேற்கண்ட சமன்பாடுகளை ஒப்பிட,

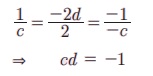
4. இரட்டை நேர்க்கோடுகளின் பொது வடிவம் (General form of pair of straight lines)

l1x + m1 y + n1 = 0 மற்றும் l2x + m2 y + n2 = 0

என்பன ஏதேனும் இரு நேர்க்கோடுகள் எனக் கருதுவோம். இக்கோடுகளின் ஒருங்கிணைந்த சமன்பாடு,

(l1x + m1 y + n1) (l2x + m2 y + n2) = 0

இவ்விரு காரணிகளை பெருக்குவதால், கிடைக்கும் இரட்டை நேர்க்கோட்டின் பொது வடிவமானது

ax2 + 2hxy + by2 + 2gx + 2fy + c = 0      (6.40) 

மேற்கண்ட சமன்பாடு, அசமபடித்தான இருபடிச் சமன்பாடாகும். 

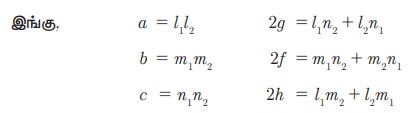
மேற்கண்ட சமன்பாடு (6.40) -ஐ l1x + m1 y + n1 = 0 மற்றும் l2x + m2 y + n2 = 0

என இரு நேரிய காரணிகளாகப் பிரிக்க முடியுமானால் சமன்பாடு (6.40)-ஐ எப்பொழுதும் இரட்டை நேர்க்கோடுகளின் சமன்பாடுகள் எனக் குறிப்பிடலாம்.

பொதுவான ஓர் இருபடிச் சமன்பாடு

ax2 + 2hxy + by2 + 2gx + 2fy + c = 0     

இரட்டை நேர்க்கோடுகளைக் குறிப்பதற்கான கட்டுப்பாட்டைக் காண்போம்.

கொடுக்கப்பட்ட இரட்டை நேர்க்கோடுகளை

ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 என்பதைக் கீழ்க்காணுமாறு x-ன் இருபடிச் சமன்பாடாக மாற்றி எழுதலாம்.

ax2 + 2(hy +g)x + (by2 + 2fy + c) = 0

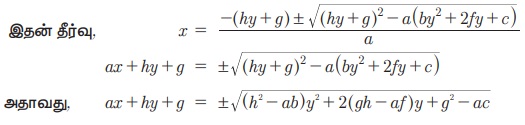
மேற்கண்ட இருசமன்பாடுகள் ஒரு நேர்க்கோட்டைக் குறிக்கிறது. எனவே, இச்சமன்பாடுகள் x மற்றும் y -ல் ஒருபடித்தான சமன்பாடுகளாகும். ஆகையால் மேற்கண்ட விரிவாக்கத்தில் படி மூலக்குறியில் உள்ள y -ன் சார்பை வர்க்கமாக (perfect square) மாற்ற இயலும். அதற்கான நிபந்தனையை பயன்படுத்த

4(gh - af)2 - 4(h2 - ab)(g2 - ac) = 0            (⸪ Δ = B2 - 4AC = 0 ) 

இதனை விரிவுபடுத்திப் பின்னர் ஒழுங்குபடுத்தி, a -யினால் வகுத்தால், abc + 2fgh – af2 – bg2 – ch2 =0 எனக் கிடைக்கும்.

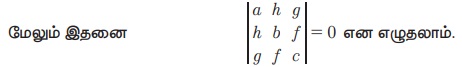
(இந்த அணிக் கோவையின் விரிவை அடுத்த இயலில் காண்போம்)

நிருபணமின்றிப் பயன்பாட்டிற்கான சில முடிவுகள்

(i) ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 என்ற இரட்டைக்கோடுகளில் உள்ள இரண்டு கோடுகளும் இணையாக உள்ளது எனில்,

(ii) ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 என்ற இரட்டை இணை நேர்கோடுகளை குறித்தால், அவ்விரு கோடுகளுக்கு இடைப்பட்ட தொலைவு, 

பொது மற்றும் திட்ட இரட்டை நேர்கோடுகளுக்கு இடையே உள்ள தொடர்பு (The relation between the equations of pair of straight lines)

ax2 + 2hxy + by2 = 0       (6.41)

ax2 + 2hxy + by2 + 2gx + 2fy + c = 0  (6.42)

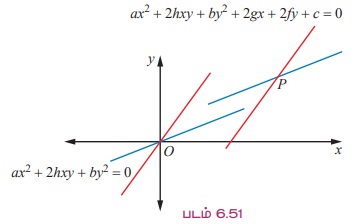
இவ்விரு இரட்டை நேர்க் கோடுகளின் சாய்வுகள் x2 , xy மற்றும் y2 -ன் குணகங்களை மட்டுமே சார்ந்திருக்கும். 

(iii) சமன்பாடு (6.41)-ன் வெட்டிக்கொள்ளும் புள்ளி (0, 0) மற்றும் சமன்பாடு (6.42)-ன் வெட்டிக்கொள்ளும் புள்ளி

(iv) கோணம் θ என்பது ax2 + 2hxy + by2 = 0 மற்றும்

ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 ஆகிய இரு இரட்டை நேர்கோடுகளின் கோணம் சமமாகும். ஆகவே,

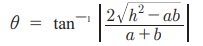
(v) ax2 + 2hxy + by2 = 0 மற்றும் ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 என்ற இரண்டு இரட்டை நேர்கோடுகள், செங்குத்துகோடுகள் எனில், a + b = 0

எடுத்துக்காட்டு 6.38 λx2 - 10xy + 12y2 + 5x - 16y - 3 = 0 என்பது ஒரு இரட்டை நேர்க்கோட்டை குறிக்கும் எனில்,

(i) λ-ன் மதிப்பு மற்றும் தனித்தனிச் சமன்பாடுகளைக் காண்க. 

(ii) இவ்விரு கோடுகள் வெட்டும் புள்ளியைக் காண்க.

(iii) இரு கோடுகளுக்கு இடைப்பட்ட கோணம் காண்க. 

தீர்வு

(i) பொதுச் சமன்பாடு ax2 + 2hxy + by2 + 2gx + 2fy + c = 0

கொடுக்கப்பட்ட சமன்பாடு, λx2 - 10xy + 12y2 + 5x - 16y - 3 = 0

மேற்கண்ட சமன்பாடுகளை ஒப்பிட, 

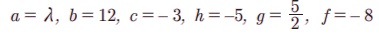
இம்மதிப்புகளை இரட்டைக் கோட்டிற்கான கட்டுப்பாட்டில் பிரதியிட,

abc + 2fgh – af2 – bg2 - ch2 = 0 

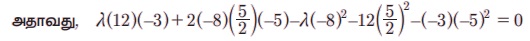
⇒    -36 λ + 200 - 64 λ - 75 + 75 = 0

⇒      λ = 2

எனவே, தேவையான சமன்பாடு, 2x2 - 10xy + 12y2 + 5x - 16y - 3 = 0.

மேற்கண்ட சமன்பாட்டில் இருபடி உறுப்புகள் 2x2 - 10xy + 12y2 -ஐ எடுத்துக்கொண்டு காரணிப்படுத்த,

2x2 - 10xy + 12y2 ≡ (x - 2y)(2x - 6y) 

எனவே 2 x2 - 10xy + 12y2 + 5x - 16y - 3 ≡  (x-2y + c1)(2x - 6y + c2) 

ஒரே மாதிரியான கெழுக்களைச் சமப்படுத்த,

2c1 + c2 = 5, 3 c1 + c2 = 8, c1 c2 = -3 

முதல் இரண்டு சமன்பாடுகளைத் தீர்வு காண்பதன் மூலம்

c1 = 3, c2 = – 1 எனக் கிடைக்கும்.

எனவே, தனித்தனிச் சமன்பாடுகள்

x – 2y + 3 = 0 , 2x – 6y - 1 = 0

(ii) இரட்டைக் கோடுகளின் வெட்டும் புள்ளியைக் காண, 

தனித்தனிச் சமன்பாடுகளைத் தீர்ப்பதன் மூலம் (x, y) = (-10, -7/2) 

அல்லது 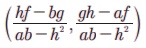என்ற சூத்திரத்தையும் பயன்படுத்திக் காணலாம். 

(iii) கோடுகளுக்கு இடைப்பட்ட கோணம்

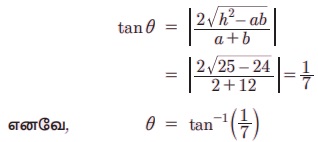
எடுத்துக்காட்டு 6.39 ஒரு மாணவன், அவனுடைய வீட்டிலிருந்து பள்ளிக்குச் சராசரியாக மணிக்கு 6 கி.மீ. வேகத்தில் நடந்து சென்றால் பள்ளி தொடங்குவதற்கு 10 நிமிடம் முன்னதாகப் பள்ளியைச் சென்றடைகிறான். அதே வேளையில், சராசரியாக மணிக்கு 4 கி.மீ வேகத்தில் நடந்து செல்லும்போது 5 நிமிடம் தாமதமாகப் பள்ளியைச் சென்றடைகிறான். அம்மாணவன் தினமும் காலை 8.00 மணிக்கு வீட்டிலிருந்து பள்ளிக்குப் புறப்பட்டுச் சென்றால் பின்வரும் வினாக்களுக்கு விடை காண்க.

(i) அவனுடைய வீட்டிற்கும் பள்ளிக்கும் இடைப்பட்ட தொலைவு 

(ii) சரியான நேரத்திற்கு அவன் பள்ளிக்குச் செல்ல ஆகும் குறைந்தபட்சச் சராசரி வேகம் மற்றும் மாணவன் பள்ளியைச் சென்றடைய ஆகும் நேரம் 

(iii) பள்ளி தொடங்கும் நேரம் 

(iv) மாணவன் நடந்து செல்லும் பாதையின் இரட்டை நேர்க்கோடுகளின் சமன்பாடு.

தீர்வு 

x - அச்சானது நேரத்தை மணியிலும், y - அச்சானது தூரத்தை கிலோமீட்டரிலும் குறிப்பிடுகிறது என்க.கொடுக்கப்பட்ட தகவலின்படி,

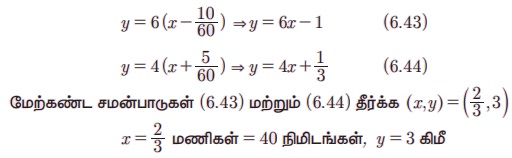
(i) அவனது பள்ளிக்கும் வீட்டிற்கும் உள்ள தொலைவு 3 கிமீ

(ii) பள்ளிக்கு நேரத்திற்குச் செல்ல எடுத்துக் கொள்ளும் குறைந்தபட்ச சராசரி

வேகம் = 60 / 40 × 3 = 4.5 கிமீ / மணி

மற்றும் பள்ளியை அடைய ஆகும் நேரம் = 2/3 மணி அல்லது 40 நிமிடம்

(iii) பள்ளி தொடங்கும் நேரம் காலை 8.40 ஆகும்.

(iv) நடைபாதையின் இரட்டை நேர்கோடுகளின் சமன்பாடு

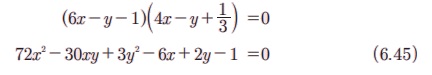
கீழே கொடுக்கப்பட்ட வலைதளத்தின் மூலம் வளைவரையை வரையலாம்.

https://www.geogebra.org/graphing, https://www.geogebra.org/m/fhS6HUtP

எடுத்துக்காட்டு 6.40 ax2 + 2hxy + by2 = 0 என்ற இரட்டைக்கோடுகளில் ஒரு கோடு px + qy = 0 -க்கு செங்குத்தாக உள்ளது எனில் ap2 + 2hpq + bq2 = 0 என நிறுவுக. 

தீர்வு

m1 மற்றும் m2 என்பன ax2 + 2hxy + by2 = 0 என்ற இரட்டை நேர்க்கோட்டின் சாய்வுகள் மற்றும் m என்பது px + qy = 0 என்ற கோட்டின் சாய்வு என்க.

எனவே,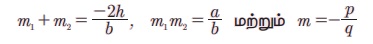

ax2 + 2hxy + by2 = 0 என்ற இரட்டைக் கோடுகளில் ஒரு கோடு, px + qy = 0 -க்கு செங்குத்தாக உள்ளதால், செங்குத்துக் கோடுகளின் நிபந்தனைகளைப் பயன்படுத்த,

mm1 = -1 அல்லது mm2 = -1 

⇒ (mm1 + 1) = 0 அல்லது (mm2 + 1) = 0

⇒ (mm1 + 1) (mm2 + 1) = 0

⇒ (m1m2)m2 (m1 + m2) m + 1 = 0

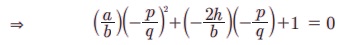
⇒  ap2 + 2hpq + bq2 = 0 என நிரூபிக்கப்பட்டது.

எடுத்துக்காட்டு 6.41 3x – 2y + 2 = 0 என்ற கோடு, 3x2 + 5xy - 2y2 + 4x + 5y = 0 என்ற இரட்டைக் கோடுகளை வெட்டும் இரு புள்ளிகளை ஆதியுடன் இணைக்கும் கோடுகள் செங்குத்தானவை எனக் காண்க.

தீர்வு

கொடுக்கப்பட்ட கோடுகள் வெட்டும் புள்ளிகளை ஆதியுடன் இணைக்கக் கிடைக்கும் கோடுகளின் சமன்பாடு ஒரு இரண்டாம் படி சமபடித்தான சமன்பாடாகும்.

3x2 + 5xy - 2y2 + 4x + 5y = 0 மற்றும் 3x – 2y  + 2 = 0 எனக் கொடுக்கப்பட்ட இரண்டு சமன்பாடுகளையும் பயன்படுத்தி சமபடித்தான சமன்பாட்டைக் காண்போம்.

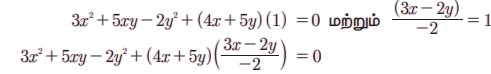
அதாவது, (- 2) (3x2 + 5xy - 2y2) + (4x + 5y) (3x - 2y) = 0 

இதனைச் சுருக்குவதால் 2x2 - xy - 2y2 = 0 எனப் பெறலாம். 

இங்கு x2 மற்றும் y2 -ன் கெழுக்களின் கூடுதல் பூச்சியமாகும்.

அதாவது, a + b = 0 , (⸪ a = 2, b = -2)

எனவே, கோடுகள் ஒன்றையொன்று செங்குத்தாக அமைகிறது.

பயிற்சி 6.4

1. x – 2y - 3 = 0 மற்றும் x + y + 5 = 0 என்ற தனித்தனிச் சமன்பாடுகளைக் கொண்ட கோடுகளின் ஒருங்கிணைந்த சமன்பாட்டைக் காண்க.

2. 4x2 + 4xy + y2 – 6x – 3y - 4 = 0 என்பது ஒரு இணை இரட்டை நேர்க்கோட்டின் சமன்பாட்டைக் குறிக்கும் எனக் காட்டுக.

3. 2x2 + 3xy – 2y2 + 3x + y + 1 = 0 என்ற கோடு ஒரு செங்குத்து இரட்டை நேர்க்கோடு எனக் காட்டுக. 

4. 2x2 - xy - 3y2 – 6x + 19y - 20 = 0 என்பது ஒன்றையொன்று வெட்டிக் கொள்ளும் கோடுகள் எனவும், அதற்கு இடைப்பட்ட கோணம் tan-1 '(5) என நிறுவுக. 

5. y = x என்ற கோட்டுடன் α கோணத்தை உடைய, ஆதி வழிச் செல்லும் இரட்டைக் கோடுகளின் சமன்பாடு x2 – 2xy sec 2α + y2 = 0 என காண்பி. 

6. 2x – 3y + 1 = 0 மற்றும் 5x + y – 3 = 0 என்ற கோடுகளுக்குச் செங்குத்தாகவும், (1,3) என்ற புள்ளி வழியாகவும் செல்லக்கூடிய இரட்டை நேர்க்கோடுகளின் சமன்பாட்டைக் காண்க.

7. கீழே கொடுக்கப்பட்டுள்ள இரட்டை நேர்க்கோடுகளின் தனித்தனி நேர்க்கோடுகளின் சமன்பாடுகளைக் காண்க. 

(i) 3x2 + 2xy – y2 = 0 

(ii) 6(x -1)2 + 5 (x -1) (y-2) – 4(y - 2)2 = 0

(iii) 2x2 – xy - 3y2 – 6x + 19y – 20 = 0 

8. ax2 + 2hxy + by2 = 0 எனும் இரட்டை நேர்க்கோடுகளில் ஒன்றின் சாய்வு மற்றதின் சாய்வைப்போல் இரண்டு மடங்கு எனில் 8h2 = 9ab என நிறுவுக. 

9. ax2 + 2hxy + by2 = 0 எனும் இரட்டை நேர்கோடுகளில் ஒன்றின் சாய்வு மற்றதின் சாய்வைப் போல் மூன்று மடங்கு எனில் 3h2 = 4ab எனக் காட்டுக.

10. x2 + 4xy + y2 = 0 என்ற இரட்டைக் கோடும் x + y - 2 = 0 என்ற சமன்பாட்டைக் கொண்ட PQ கோடும், ΔOPQ -ஐ உருவாக்குகிறது எனில், O -லிருந்து வரையப்படும் ΔOPQ -ன் நடுகோட்டின் சமன்பாட்டைக் காண்க.

11. 6x2 + 5xy – py2 +7x + qy - 5 = 0 என்பவை ஒன்றுக்கொன்று செங்குத்தாக இருக்கும் இரட்டை நேர்க்கோடுகள் எனில், p மற்றும் q -ன் மதிப்புகளைக் காண்க. 

12. 12x2 + 7xy - 12y2 - x + 7y + k = 0 என்ற சமன்பாடு இரட்டை நேர்கோட்டுகளின் சமன்பாட்டைக் குறித்தால் k -ன் மதிப்பைக் காண்க. மேலும் அவை இணையா? அல்லது வெட்டிக் கொள்பவையா? எனக் காண்க.

13. 12x2 + 2kxy + 2y2 + 11x - 5y + 2 = 0 என்ற சமன்பாடு இரட்டை நேர்க்கோட்டின் சமன்பாட்டைக் குறித்தால் k -ன் மதிப்பைக் காண்க.

14. 9x2 - 24xy + 16y2 – 12x + 16y - 12 = 0 என்பது இணையான இரட்டை நேர்க்கோடுகள் என நிறுவுக. மேலும் இவ்விரு கோடுகளுக்கு இடைப்பட்ட தூரத்தைக் காண்க. 

15. 4x2 + 4xy + y2 – 6x - 3y - 4 = 0 என்ற இரட்டைக் கோடுகள் இணையானவை எனக் காட்டுக. மேலும், இவ்விரு கோடுகளுக்கு இடைப்பட்ட தூரத்தைக் காண்க. 

16. ax2 + 2hxy + by2 = 0 இவற்றில் ஒரு கோடு ஆய அச்சுகளுக்கு இடைப்பட்ட கோணத்தின் இருசமவெட்டி எனில் (a + b)2 = 4h2 என நிறுவுக. 

17. x2 - 2kxy – y2 = 0 என்ற இரட்டை நேர்க்கோடு x2 – 2lxy – y2 = 0 -ன் கோணங்களின் இருசமவெட்டி எனில், இரண்டாவதாகக் குறிப்பிட்ட கோடுகளும் முதலாவதாகக் குறிப்பிட்ட கோடுகளின் கோணங்களின் இருசமவெட்டி எனக் காண்பி.

18. 3x – 2y 1 = 0 என்ற நேர்க்கோடு 3x2 + 5xy – 3y2 + 2x + 3y = 0 என்ற இரட்டைக் கோடுகளை வெட்டும் இருபுள்ளிகளை ஆதியுடன் இணைக்கும் கோடுகள் செங்குத்தானவை எனக் காண்க.

பயிற்சி 6.5

சரியான அல்லது மிகவும் ஏற்புடைய விடையினைத் தேர்ந்தெடுக்கவும்

1. ஒரு புள்ளிக்கும் y அச்சிற்கும் இடைப்பட்ட தூரமானது, அப்புள்ளிக்கும் ஆதிக்கும் இடைப்பட்ட தூரத்தில் பாதி எனில் அப்புள்ளியின் நியமப்பாதை

(1) x2 + 3y2 = 0 

(2) x2 - 3y2 = 0 

(3) 3x2 + y2 = 0 

(4) 3x2 - y2 = 0 

2. (at2, 2at) என்ற புள்ளியின் நியமப்பாதை

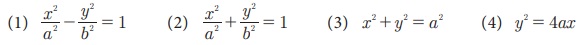
3. 3x2 + 3y2 - 8x - 12y + 17 = 0 என்ற நியமப்பாதையின் மீது அமைந்திருக்கும் புள்ளி

(1) (0,0) 

(2) (-2, 3) 

(3) (1, 2) 

(4) (0,-1) 

4. 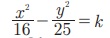என்ற நியமப்பாதையின் மீது (8,-5) என்ற புள்ளி உள்ளது எனில், k –ன் மதிப்பு 

(1) 0

(2) 1 

(3) 2 

(4) 3 

5. (2, 3) மற்றும் (-1, 4) என்ற புள்ளிகளை இணைக்கும் நேர்க்கோட்டின் மீது (α, β) என்ற புள்ளி இருந்தால் 

(1) α + 2 β = 7 

(2) 3α + β = 9 

(3) α + 3 β = 11 

(4) 3α + β = 11

6. 3x - y = -5 என்ற கோட்டுடன் 45° கோணம் ஏற்படுத்தும் கோட்டின் சாய்வுகள்

(1) 1, -1 

(2) 1/2, -2 

(3) 1, 1/2 

(4) 2, -1/2 

7. 4 + 2√2 என்ற சுற்றளவு கொண்ட முதல் கால் பகுதியில் ஆய அச்சுகளுடன் அமையும் இருசமபக்க முக்கோணத்தை உருவாக்கும் கோட்டின் சமன்பாடு 

(1) x + y + 2 = 0 

(2) x + y - 2 = 0 

(3) x + y - √2 = 0 

(4) x + y + √2 = 0

8. (-2, 4), (-1,2), (1,2) மற்றும் (2, 4) என்ற வரிசையில் நாற்கரத்தின் நான்கு முனைப்புள்ளிகளை எடுத்துக் கொள்க. ஒரு கோடு (-1, 2) என்ற புள்ளி வழியே செல்கிறது. மேலும் அது நாற்கரத்தை சமபரப்பாக பிரிக்கிறது எனில், அதன் சமன்பாடு,

(1) x + 1 = 0 

(2) x + y = 1 

(3) x + y + 3 = 0 

(4) x - y + 3 = 0 

9. (1, 2) மற்றும் (3, 4) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத்துண்டின் செங்குத்து இருசமவெட்டியானது ஆய அச்சுகளுடன் ஏற்படுத்தும் வெட்டுத் துண்டுகள் 

(1) 5, -5

(2) 5 , 5 

(3) 5, 3

(4) 5, -4

10. சாய்வு 2 உடைய கோட்டிற்கு ஆதியிலிருந்து வரையப்படும் செங்குத்துக் கோட்டின் நீளம் √5 எனில், அக்கோட்டின் சமன்பாடு 

(1) x -2y = √5 

(2) 2x - y = √5 

(3) 2x - y = 5 

(4) x -2y - 5 = 0

11. 5x - y = 0 என்ற கோட்டிற்குச் செங்குத்துக் கோடு ஆய அச்சுகளுடன் அமைக்கும் முக்கோணத்தின் பரப்பு 5 ச. அலகுகள் எனில் அக்கோட்டின் சமன்பாடு 

12. x - y + 5 = 0 என்ற கோட்டிற்குச் செங்குத்தாகவும் y அச்சை வெட்டும் புள்ளி வழியே செல்லக்கூடியதுமான நேர்க்கோட்டின் சமன்பாடு 

(1) x - y - 5 = 0 

(2) x + y - 5 = 0 

(3) x + y + 5 = 0 

(4) x + y + 10 = 0

13. ஒரு சமபக்க முக்கோணத்தின் ஒரு முனை (2, 3) மற்றும் இப்புள்ளிக்கு எதிர்ப்புறம் அமையும் பக்கத்தின் சமன்பாடு x + y = 2 எனில் பக்கத்தின் நீளம் 

(1)

(2) 6

(3) √6 

(4) 3√2 

14. p மற்றும் q ஆகியவற்றின் எந்த மதிப்புகளுக்கும் (p +2q)x+(p - 3q) y = q என்ற கோட்டின் மீது அமையும் புள்ளி

15. (1, 2) மற்றும் (3, 4) ஆகிய இரு புள்ளியிலிருந்து சமத் தொலைவிலும், 2x - 3y = 5 என்ற கோட்டின் மீதும் அமைந்துள்ள புள்ளி (1) (7, 3) 

(2) (4, 1) 

(3) (1, -1) 

(4) (-2, 3)

16. y = -x என்ற கோட்டிற்கு (2, 3) என்ற புள்ளியின் பிம்பப்புள்ளி

(1) (-3, -2) 

(2) (-3, 2) 

(3) (-2, -3) 

(4) ( 3, 2) 

17. 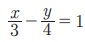என்ற கோட்டிற்கு ஆதியிலிருந்து செங்குத்துத் தொலைவு

18. 2x - 3y + 1 = 0 என்ற கோட்டிற்குச் செங்குத்தாகவும் (1, 3) என்ற புள்ளி வழியே செல்லும் நேர்க்கோட்டின் y வெட்டுத்துண்டு

19. x + (2k - 7)y + 3 = 0 மற்றும் 3kx + 9y - 5 = 0 இவ்விரு கோடுகள் செங்குத்தானவை எனில் k-ன் மதிப்பு

20. ஒரு சதுரத்தின் ஒரு முனை ஆதியாகவும் மற்றும் அதன் ஒரு பக்கம் 4x + 3y - 20 = 0 என்ற கோட்டின் மீதும் அமைந்திருந்தால், அந்தச் சதுரத்தின் பரப்பு 

(1) 20 சஅ

(2) 16 சஅ 

(3) 25 சஅ 

(4) 4 சஅ 

21. 6x2 + 41xy – 7y2 = 0 என்ற இரட்டைக் கோடுகள் x- அச்சுடன் ஏற்படுத்தும் கோணங்கள் α மற்றும் β எனில், tan α tan β = ? 

22. x2 - 4y2 = 0 மற்றும் x = a என்ற கோடுகளால் உருவாக்கப்படும் முக்கோணத்தின் பரப்பு

23. 6x2 - xy + 4cy2 = 0 என்ற கோடுகளில் ஒரு கோடானது 3x + 4y = 0 எனில் c - ன் மதிப்பு 

(1) -3 

(2) -1 

(3) 3

(4) 1

24. x2– xy – 6y2 = 0 என்ற கோடுகளுக்கு இடைப்பட்ட குறுங்கோணம் θ எனில் 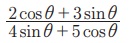-ன் மதிப்பு

25. x2– 2xycot θ – y2 = 0 என்ற இரட்டை நேர்க்கோட்டின் சமன்பாடுகளில் ஒரு சமன்பாடு 

(1) x - ycot θ = 0

(2) x + ytan θ = 0 

(3) xcos θ + y (sin θ + 1) = 0

(4) xsin θ + y (cos θ + 1) = 0