ஒரு புள்ளியின் நியமப்பாதை

ஒரு புள்ளியின் நியமப்பாதை (Locus of a point)

வரையறை 6.1

ஒரு புள்ளி (point) என்பது ஒரு தளத்தின் மேற்பரப்பில் உள்ள ஒரு (குறிப்பிட்ட இடத்தை (location) குறிப்பதாகும். புள்ளியானது ஒரு பொருளையோ அல்லது வடிவத்தையோ குறிப்பதல்ல.

இருபரிமாணபகுமுறை வடிவியலில் புள்ளிகளை ஆயத்தொலை அமைப்பு முறையில் மெய்யெண்களின் வரிசைப்படுத்தப்பட்ட சோடிகளாக அதாவது (x, y) எனக் குறிப்பிடுகிறோம். பொதுவாக, கிடைமட்டக் கோட்டை x -அச்சு எனவும் x -அச்சுக்கு செங்குத்தான கோட்டை y- அச்சு எனவும் அழைக்கிறோம். இவ்விரு அச்சுகளின் வெட்டும் புள்ளியை ஆதிப்புள்ளி அல்லது ஆதி என அழைக்கிறோம். ஒரு தளத்தின் மீது ஏதேனும் ஒரு புள்ளி P-யை ஒரு தனித்த வரிசைப்படுத்தப்பட்ட சோடி (x, y) எனக் குறிப்பிடலாம். இங்கு x என்பது புள்ளி P - க்கும் y - அச்சுக்கும் இடைப்பட்ட தொலைவு மற்றும் y என்பது புள்ளி P - க்கும் x - அச்சுக்கும் இடைப்பட்ட தொலைவு ஆகும். y - அச்சின் இடப்புறத்தில் x குறை மதிப்பு கொண்டதாகவும் இதேபோன்று, x - அச்சிற்குக் கீழ்புறம் y குறை மதிப்பாக இருக்கும். பயன்பாட்டின்போது x மற்றும் y -க்குப் பதிலாக வேறு எழுத்துக்களையும் பயன்படுத்தலாம். மேலும், அச்சுகளுக்கு வெவ்வேறு அளவுத்திட்டங்களையும் பயன்படுத்தலாம்.

வரையறை 6.2

ஒரு புள்ளியானது சில குறிப்பிட்ட நிபந்தனைகளுக்கு உட்பட்டு இயங்கும்போது, அப்புள்ளி நகர்ந்து செல்லும் பாதை அதன் நியமப்பாதை (Locus) எனப்படும்.

கீழ்காணும் விளக்க எடுத்துக்காட்டுகளில் நியமப்பாதை மற்றும் அதன் பயன்களை பற்றியும் அறியலாம்.

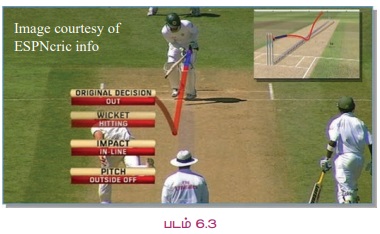
விளக்க எடுத்துக்காட்டு 6.1 கிரிக்கெட் விளையாட்டில் பந்து வீசுபவர், ஒரு பந்தை வீசும்போது அப்பந்து செல்லும் பாதை அதன் நியமப்பாதையாகும். பந்து வீசுபவர் மூலம் வீசியபந்தை மட்டையாளர் காலில் தடுத்தாடும் போது, பந்து வீசும் அணியினருக்கும் மட்டையாளருக்கும், இடையே ஏற்படும் பிரச்சனைக்கு (LBW) தீர்வுகாண மூன்றாவது நடுவரின் முடிவுக்கு விடப்படும். அவர் பந்து செல்லும் பாதையைத் திரையில் மெதுவாக இயக்கச் செய்து அப்பந்து மட்டையாளர் காலில் பட்டு பின்னர் ஸ்டம்பில் பட வாய்ப்பு உள்ளதா எனச் சரிபார்த்து பின்னர் சரியான முடிவினை அறிவிப்பார். இங்கு பந்து புள்ளியாகவும் அப்பந்து செல்லும் பாதை நியமப்பாதையாகவும் கருதப்படுகிறது. இம்முறையானது அகில உலகக் கிரிக்கெட் போட்டிகளில் தற்போது அனுமதிக்கப்படுகிறது.

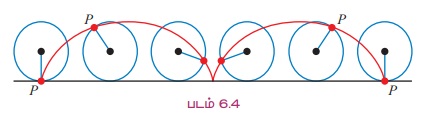
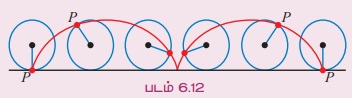
விளக்க எடுத்துக்காட்டு 6.2 P என்ற ஒரு புள்ளியானது ஒரு வட்டத்தின் விளிம்பில் உள்ளது என்க. அந்த வட்டமானது ஒரு நேர்க்கோட்டின் மீது சறுக்கி (நழுவி) செல்லாமல் உருண்டு செல்கிறது. அவ்வாறு உருண்டு செல்லும்போது வட்டத்தின் விளிம்பில் உள்ள P என்ற புள்ளி உருவாக்கும் நியமப்பாதையை உருள்வளை (cycloid) என அழைக்கலாம். இவ்வளைவரையை www.mathuorld. wolfram.com/cgloid மற்றும் (uuu.gogebra.org/b/bd2ADu2I வளைதளத்தில் காணலாம்.

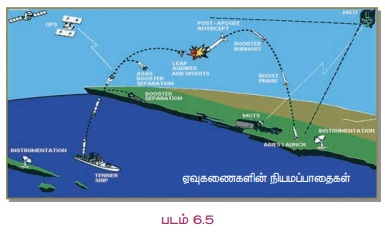
விளக்க எடுத்துக்காட்டு 6.3 ஒரு இலக்கைத் தாக்குவதற்கு இராணுவக்கப்பலில் இருந்து ஒரு ஏவுகணை ஏவப்படுகிறது. எதிர்வரும் ஏவுகணையை இடைமறித்து அழிக்கத் தரையில் இருந்து மற்றொரு ஏவுகணை ஏவப்படுகிறது. ஏவுகணைகளின் நியமப்பாதைகள் படத்தில் காட்டப்பட்டுள்ளன. இது போன்ற நிகழ்வுகள் பல போர்களில் முன் கூட்டியே துல்லியமாக நடைமுறைப்படுத்த நியமப்பாதையின் கருத்தாக்கம் மிக முக்கியப் பங்கு வகிக்கிறது. வளைகுடா போரின் (2 ஆகஸ்ட் 1990 முதல் 28 பிப்ரவரி 1991 முடிய) போது இஸ்ரேலின் நகரங்களை ஈராக் ஸ்கட் (Scud) ரக ஏவுகணைகளை கொண்டு தாக்கியது. அவற்றை இடைமறித்து அழிக்க இஸ்ரேல் பேட்ரியாட் (Patriot) ரக ஏவுகணைகளைப் பயன்படுத்தியது.

உலக அரங்கில் விண்வெளி ஆராய்ச்சியாளர்கள் செயற்கைக் கோளை வெற்றிகரமாக விண்ணில் செலுத்துவதற்கும் அதன் சுற்று வட்டப் பாதையில் நிலை நிறுத்துவதற்கும் நியமப்பாதையின் கருத்தாக்கம் முக்கியப் பங்கு வகிக்கிறது.

x மற்றும் y என்ற இரு மாறிகளைக் கொண்ட சமன்பாட்டைச் சாதாரணமாக x மற்றும் y ஆகிய மெய்மதிப்புக்களை கொண்ட எண்ணற்ற ஜோடிகள் நிறைவு செய்கின்றன. நிறைவு செய்யும் ஒவ்வொரு ஜோடியும் அச்சமன்பாட்டின் மெய்யெண் தீர்வு எனப்படும். சமன்பாட்டின் ஒவ்வொரு மெய்யெண் தீர்வும் அதனுடைய வரைபடத்தைப் பெற்றிருக்கும். இவ்வரைபடங்களின் தொகுப்பு கொடுக்கப்பட்ட சமன்பாட்டின் நியமப்பாதை எனப்படும்.

கணிதத்தில் உள்ள சில முக்கிய நியமப்பாதைகள் பின்வரும் அட்டவணையில் கொடுக்கப்பட்டுள்ளன.

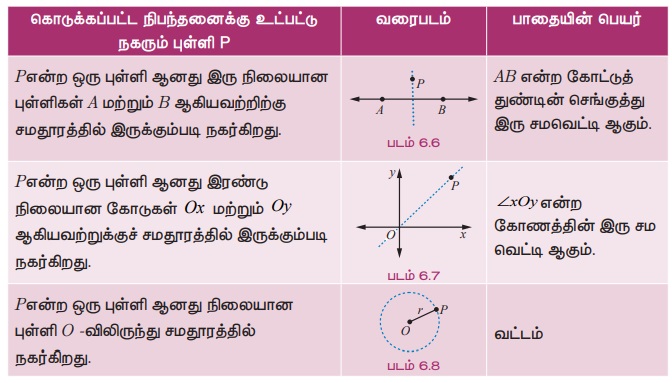
ஒரு புள்ளியின் நியமப்பாதையை காணும் வழிமுறைகளைப் பற்றி இங்கு விவாதிக்கலாம். நியமப்பாதையின் சமன்பாடு என்பது அப்பாதையில் அமைந்துள்ள அனைத்து புள்ளிகளின் ஆயத்தொலைவுகளுக்கு இடையே உள்ள தொடர்பு ஆகும்.

ஒரு புள்ளியின் நியமப் பாதையின் சமன்பாடு காணும் செயல்முறைகள் 

(i) P என்ற புள்ளியின் நியமப் பாதையைக் காண வேண்டும் எனில் புள்ளி P –ன் ஆயக்கூறுகளை (h, k) என எடுத்துக் கொள்க. 

(ii) தெரிந்த அளவுகளையும் மற்றும் தெரியாத துணையலகுகளையும் (Parameter) பயன்படுத்திக் கொடுக்கப்பட்ட நிபந்தனைகளை சமன்பாடுகளாக எழுதுக. 

(iii) தெரியாத துணையலகுகளை நீக்கி h, k மற்றும் தெரிந்த அளவுகள் மட்டும் இருக்குமாறு சமன்பாட்டைக் காண்க. 

(iv) கிடைக்கும் சமன்பாட்டில் h-க்கு பதிலாகா x மற்றும் k -க்கு பதிலாக y எனப் பிரதியிடக் கிடைக்கும் சமன்பாடு புள்ளி p-ன் நியமப்பாதையின் சமன்பாடாகும்.

எடுத்துக்காட்டு 6.1 x -அச்சிலிருந்து உள்ள தொலைவானது y -அச்சுலிருந்து உள்ள தொலைவுக்கு சமமாக இருக்குமாறு நகரும் ஒரு புள்ளியின் நியமப்பாதையைக் காண்க.

தீர்வு

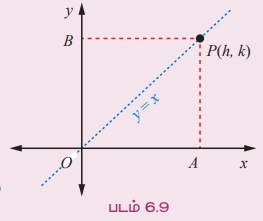
P(h,k) என்பது நியமப்பாதையின் மீது அமைந்துள்ள ஏதேனும் ஒரு புள்ளி என்க.

புள்ளி P-லிருந்து x மற்றும் y-அச்சுகளுக்கு வரையப்படும் செங்குத்துக்கோடுகளின் அடிப்புள்ளிகள் முறையே A, B என்க.

புள்ளி P என்பது (OA, OB) = (BP, AP) = (h,k) 

கொடுக்கப்பட்ட நிபந்தனையின்படி,

AP = BP ⇒ k = h

h = x மற்றும் k = y ஐப் பிரதியிட

P-ன் நியமப்பாதை y = x என்ற ஆதி வழியே செல்லும் கோடாகும்.

எடுத்துக்காட்டு 6.2 (ct, c/t) என்ற புள்ளி நகர்வதால் உண்டாகும் பாதையைக் காண்க.

இங்கு t ≠ 0 என்பது துணையலகு மற்றும் c என்பது ஒரு மாறிலியாகும். 

தீர்வு

தேவையான நியமப்பாதையின் மீதுள்ள ஏதேனும் ஒரு புள்ளி P(h,k) என்க. 

கொடுக்கப்பட்ட விவரங்களிலிருந்து, h = ct மற்றும் k = c/t ஆகும். 

இவ்விரு சமன்பாடுகளைப் பெருக்கி t-ஐ நீக்கலாம்.

(h)(k) = (ct)(c/t) ⇒ hk = c2 , h = x மற்றும் k = y எனப் பிரதியிட 

ஃ தேவையான நியமப்பாதையின் சமன்பாடு xy = c2

எடுத்துக்காட்டு 6.3 A(1, 0) மற்றும் B(5,0) என்ற புள்ளிகளிலிருந்து சம தூரத்திலிருக்குமாறு நகரும் புள்ளியின் நியமப்பாதையின் சமன்பாட்டைக் காண்க.

தீர்வு

கொடுக்கப்பட்ட இரு புள்ளிகள் A(1, 0) மற்றும் B(5,0) ஆகும்.

P(h,k) என்பது தேவையான பாதையின்மீது அமைந்துள்ள ஏதேனும் ஒரு புள்ளி என்க.

கொடுக்கப்பட்ட நிபந்தனையின்படி, AP = BP

அதாவது

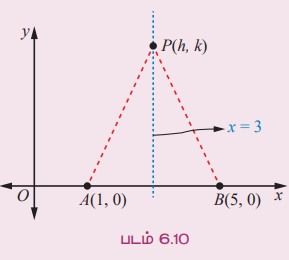
⇒ h = 3

எனவே, புள்ளி P(h,k) -ன் நியமப்பாதை, x = 3 

இது y-அச்சிற்கு இணையாக உள்ள நேர்க்கோடு ஆகும்.

எடுத்துக்காட்டு 6.4 (a sec θ, b tan θ) என்ற நகரும் புள்ளியின் நியமப்பாதையின் சமன்பாட்டைக் காண்க. இங்கு θ என்பது துணையலகு ஆகும். 

தீர்வு

P(h,k) என்பது தேவையான பாதையின் மீது அமைந்துள்ள ஏதேனும் ஒரு புள்ளி என்க.

கொடுக்கப்பட்ட நிபந்தனையின்படி

குறிப்பு: துணையலகானது முக்கோணவியல் அமைப்பில் இருப்பின் கீழ்க்காணும் முற்றொருமைகளைப் பயன்படுத்தி துணையலகுகளை நீக்கலாம்.

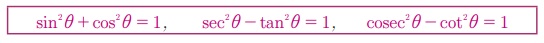
எடுத்துக்காட்டு 6.5 நீளம் 6 அலகுகள் கொண்ட ஒரு நேரான கம்பியின் முனைகள் A மற்றும் B ஆனது முறையே எப்போதும் x மற்றும் y-அச்சுகளைத் தொடுமாறு நகர்கிறது. O-ஐ ஆதியாகக் கொண்ட Δ OAB என்ற முக்கோணத்தின் நடுப்புள்ளியின் (centroid) நியமப்பாதையின் சமன்பாட்டைக் காண்க

தீர்வு

P(h,k) என்பது தேவையான பாதையின் மீதுள்ள ஏதேனும் ஒரு புள்ளி என்க.

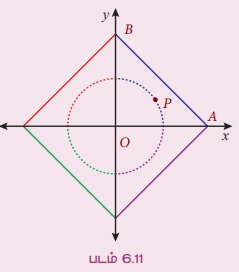
O, A மற்றும் B ஆகிய புள்ளிகளின் ஆயக் கூறுகள் முறையே (0, 0), (a,0) மற்றும் (0, b) என்க. 

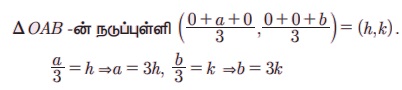
செங்கோணம் ΔBOA -லிருந்து

OA2 + OB2 = AB2

(3h)2 + (3k)2 = (6)2 ⇒ h2 + k2 = 4 

எனவே, P(h,k) என்ற புள்ளியின் நியமப்பாதை, x2 + y2 = 4.

எடுத்துக்காட்டு 6.6 நகரும் புள்ளியின் ஆயக்கூறு (a ( θ – sin θ ), a (1- cos θ )) இங்கு θ என்பது துணையலகு எனில், இப்புள்ளி நகரும் நியமப்பாதையின் சமன்பாட்டைக் காண்க. 

தீர்வு 

P(h,k) என்பது தேவையான நியமப்பாதையின் மீதுள்ள ஏதேனும் ஒரு புள்ளி என்க.

h = a (θ – sin θ )   (6.1)

k = a (1 – cos θ )   (6.2) 

மேற்கண்ட சமன்பாடு (6.2) இலிருந்து θ மற்றும் sin θ மதிப்புகளைக் காணலாம்.

k = a (1 - cos θ ) 

குறிப்பு: மேற்கூறிய சமன்பாடானது துணையலகு வடிவத்திலிருந்து கார்டீசியன் வடிவத்திற்கு மாற்றப்பட்டுள்ளது. ஆனால் சில நேரங்களில் கார்டீசியன் வடிவத்தைவிடத் துணையலகு வடிவமே கையாள்வதற்கு எளிதாக பயன்படுகிறது.

பயிற்சி 6.1

1. கீழே கொடுக்கப்பட்டுள்ள ஆயத்தொலைகளை உடைய நகரும் புள்ளி P-ன் நியமப்பாதையின் சமன்பாட்டைக் காண்க. இங்கு α ஒரு துணையலகு ஆகும்.

(i) (9 cos α, 9 sin α ) 

(ii) (9 cos α, 6 sin α ) 

2. (i) x-அச்சிலிருந்து இரண்டு அலகுகள் மற்றும் (ii) y -அச்சிலிருந்து மூன்று அலகுகள் என்ற மாறாத தொலைவில் நகரும் புள்ளி P -ன் நியமப்பாதையின் சமன்பாட்டைக் காண்க.

3. θ ஒரு துணையலகு எனில், x = a cos2 θ, y = a sin3θ ஆகிய ஆயத்தொலைகளை உடைய நகரும் புள்ளியின் நியமப்பாதையின் சமன்பாட்டைக் காண்க.

4. x2 – 5x + ky = 0 என்ற நியமப்பாதையின் மீது புள்ளிகள் P(-3,1) மற்றும் Q(2,b) அமையும் எனில் k மற்றும் b-ன் மதிப்புகளைக் காண்க.

5. 8 அலகுகள் நீளமுள்ள ஒரு நேரான கம்பியின் முனைகள் A மற்றும் B ஆகியவை முறையே எப்போதும் x மற்றும் y-அச்சுகளைத் தொடுமாறு நகர்ந்து கொண்டு இருக்கிறது, எனில் வெட்டுத்துண்டு AB - ன் நடுப்புள்ளியின் நியமப்பாதையின் சமன்பாட்டைக் காண்க.

6. (3, 5) மற்றும் (1,-1) என்ற புள்ளிகளிலிருந்து ஒரு நகரும் புள்ளிக்கு இடைப்பட்ட தொலைவுகளின் வர்க்கங்களின் கூடுதல் 20-க்கு சமம் எனில் அப்புள்ளியின் நியமப்பாதையின் சமன்பாட்டைக் காண்க.

7. A(1,-6) மற்றும் B(4,-2) என்ற புள்ளிகளை இணைக்கும் AB கோட்டுத் துண்டானது புள்ளி P-ல் தாங்கும் கோணம் செங்கோணம் எனில், புள்ளி P -ன் நியமப்பாதையின் சமன்பாட்டைக் காண்க.

8. ஆதிப்புள்ளி O என்க. y2 = 4x என்ற வளைவரையின் மீது மாறிப்புள்ளி R அமைந்துள்ளது எனில் கோட்டுத்துண்டு OR -ன் நடுப்புள்ளியின் நியமப்பாதையின் சமன்பாட்டைக் காண்க. 

9. நகரும் புள்ளி P-ன் ஆயக் கூறுகள் 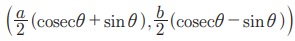எனில், P-ன் நியமப்பாதையின் சமன்பாடு b2x2 - a2y2 = a2b2 எனக் காட்டுக. இங்கு θ என்பது ஒரு துணையலகு மாறி ஆகும்.

10. Q என்ற புள்ளி 2x2 + 9y2 = 18 என்ற வளைவரையின் மீது அமைந்துள்ளது. P(2,-7) கொடுக்கப்பட்ட புள்ளி எனில் கோட்டுத்துண்டு PQ-ன் நடுப்புள்ளியின் நியமப்பாதையின் சமன்பாட்டைக் காண்க.

11. R மற்றும் Q என்பன முறையோ x மற்றும் y -அச்சுகளின் மீது அமைந்துள்ள புள்ளிகள், P என்ற நகரும் புள்ளி RQ-ன் மேல் உள்ளது. மேலும் RP = b, PQ = a என்றவாறு RQ-ன் மீது அமைந்துள்ள நகரும் P-ன் நியமப்பாதையின் சமன்பாட்டைக் காண்க. 

12. P(6 , 2), Q(-2, 1) மற்றும் R என்பன ΔPQR-ன் முனைப் புள்ளிகள் மற்றும் நியமப்பாதை y = x2 – 3x + 4 -ன் மீது R என்ற புள்ளி அமைந்துள்ளது எனில், ΔPQR -ன் மையக்கோட்டுச் சந்தியின் (Centroid) நியமப்பாதையின் சமன்பாட்டைக் காண்க. 

13. x2 + y2 + 4x – 3y + 7 = 0 என்ற நியமப்பாதையின் மீது Q என்ற புள்ளி அமைந்துள்ளது. P என்ற புள்ளி கோட்டுத் துண்டு OQ-ஐ வெளிப்புறமாக 3:4 என்ற விகிதத்தில் பிரிக்கும் எனில் புள்ளி P-ன் நியமப்பாதையின் சமன்பாட்டைக் காண்க. இங்கு O என்பது ஆதிப்புள்ளியாகும். 

14. கொடுக்கப்பட்ட P(5,1) புள்ளிக்கு 5 அலகுகள் மற்றும் x -அச்சிலிருந்து 3 அலகுகள் தூரம் கொண்ட ஒரு நியமப்பாதையின் மீது அமைந்துள்ள புள்ளிகள் எத்தனை? மேலும் அப்புள்ளிகளைக் காண்க.

15. (-4, 0) மற்றும் (4,0) ஆகிய புள்ளிகளிலிருந்து ஒரு நகரும் புள்ளிக்கு இடைப்பட்ட தொலைவுகளின் கூடுதல் எப்போதும் 10 அலகுகள் எனில், நகரும் புள்ளியின் நியமப்பாதையின் சமன்பாட்டைக் காண்க.