பல்லுறுப்புக் கோவைகளின் மீ.பொ.வ மற்றும் மீ.பொ.ம.

பல்லுறுப்புக் கோவைகளின் மீ.பொ.வ மற்றும் மீ.பொ.ம. (GCD and LCM of Polynomials) 

3.3.1 மீப்பெரு பொது வகுத்தி (அ) மீப்பெரு பொதுக் காரணி (Greatest Common Divisor (or) Highest Common Factor)

நாம் முந்தைய வகுப்பில் இரண்டாம் படி மற்றும் மூன்றாம் படி பல்லுறுப்புக் கோவைகளுக்குக் காரணி முறையில் மீ.பொ.வ (மீ.பொ.கா) காண்பதைக் கற்றோம். தற்போது நாம் நீள் வகுத்தல் முறையில் பல்லுறுப்புக் கோவைகளின் மீ.பொ.வ எவ்வாறு காண்பது எனக் கற்க உள்ளோம்.

இரண்டாம் பாடத்தில் (எண்களும் தொடர் வரிசைகளும்) விவாதித்தபடி, யூக்ளிடின் வகுத்தல் வழிமுறையைப் பயன்படுத்தி இரண்டு மிகை முழுக்களின் மீ.பொ.வ கண்டறிந்த அதே முறையைப் பயன்படுத்தி இரு பல்லுறுப்புக் கோவைகளின் மீ.பொ.வ கண்டறியலாம்.

f(x) மற்றும் g(x) என்ற பல்லுறுப்புக் கோவைகளின் மீப்பெரு பொது வகுத்தி காணப் பின்வரும் படிமுறைகள் உதவும். 

படி 1: முதலில் f(x) ஐ g(x) ஆல் வகுக்கும்போது f (x) = g (x ) q (x ) + r (x), இங்கு q(x) என்பது ஈவு, r(x) என்பது மீதி எனக் கிடைக்கிறது. r(x) -யின் படி < q (x ) -யின் படி என இருக்கும்.

படி 2: மீதி r(x) பூச்சியமில்லையெனில், g(x) ஐ r(x) - ஆல் வகுக்கும்போது g(x) = r (x)q1 (x) + r1 (x) இங்கு r1 (x) என்பது புதிய மீதி ஆகும். 

r1 (x) -யின் படி < r(x) -யின் படி, மீதி, r1(x) பூச்சியமெனில், r(x) என்பது தேவையான மீ.பொ.வ ஆகும். 

படி 3: r1(x) பூச்சியமில்லை எனில், இதே செயல்பாட்டை மீதி பூச்சியம் வரும் வரை தொடரவேண்டும். இந்த நிலையில் இருக்கும் வகுத்தியே கொடுக்கப்பட்ட பல்லுறுப்புக் கோவைகளின் மீ.பொ.வ ஆகும்.

f (x), g(x) என்ற பல்லுறுப்புக் கோவைகளின் மீ.பொ.வ வை மீ.பொ.வ [f (x), g(x)] எனக் குறிக்கலாம்.

குறிப்பு

f (x) மற்றும் g(x) இரண்டும் ஒரே படியில் அமைந்த பல்லுறுப்புக் கோவைகள் எனில் பெரிய எண்ணைத் தலையாயக் கெழுவாகக் கொண்ட கோவையை வகுபடும் கோவையாக எடுக்க வேண்டும். ஒருவேளை, தலையாயக் கெழு சமமாக இருந்தால், அதற்கடுத்த படியில் அமைந்த உறுப்பின் கெழுக்களை ஒப்பிட்டு வகுத்தலைத் தொடரவேண்டும்.

முன்னேற்றச் சோதனை

1. ஒரே படியுள்ள இரு பல்லுறுப்புக் கோவைகளை வகுக்கும்போது, ____ ஐப் பொறுத்து வகுபடும் மற்றும் வகுக்கும் கோவைகளைத் தீர்மானிக்க வேண்டும். 

2. f(x) ஐ g(x) ஆல் வகுக்கும் போது மீதி r(x) = 0 எனில், g(x) ஆனது அந்த இரு பல்லுறுப்புக் கோவைகளின் ______ என அழைக்கப்படும். 

3. f(x) = g (x)q (x) + r (x), எனில், f(x) ஆனது g (x) - ஆல் மீதியின்றி வகுபட வேண்டுமெனில், f(x) உடன் _______ ஐக் கூட்ட வேண்டும். 

4. f (x) = g (x )q (x ) + r (x), எனில், f(x) ஆனது g (x) - ஆல் மீதியின்றி வகுபட வேண்டுமெனில் f (x) உடன் ______ ஐக் கழிக்க வேண்டும்.

எடுத்துக்காட்டு 3.10 

x3 + x2 − x + 2 மற்றும் 2x3 − 5x2 + 5x – 3 ஆகிய பல்லுறுப்புக் கோவைகளின் மீ.பொ.வ காண்க. 

தீர்வு 

f (x) = 2x 3 − 5x 2 + 5x – 3 மற்றும் g (x) = x 3 + x 2 − x + 2

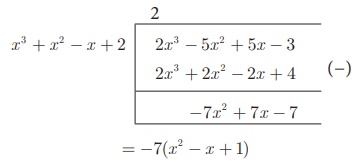
− 7(x 2 − x + 1) ≠ 0, -7 என்பது g (x) -யின் ஒரு வகுத்தி அல்ல.

g (x) = x3 + x2 − x + 2 -ஐ மீதியால் வகுக்க (மாறிலிக் காரணியை விடுத்து), நாம் பெறுவது

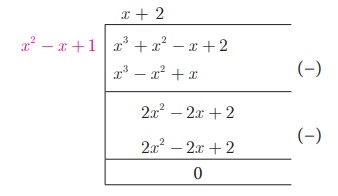
இங்கு, மீதி பூச்சியம் ஆகும். 

எனவே, மீ.பொ.வ (2x 3 − 5x 2 + 5x − 3, x 3 + x 2 − x + 2) = x 2 − x + 1.

எடுத்துக்காட்டு 3.11 

6x 3 − 30x 2 + 60x − 48 மற்றும் 3x 3 − 12x 2 + 21x −18. ஆகிய பல்லுறுப்புக் கோவைகளின் மீ.பொ.வ காண்க. 

தீர்வு 

f (x) = 6x³ − 30x² + 60x − 48 = 6(x³ − 5x² + 10x − 8) மற்றும்

g (x) = 3x³− 12x²+ 21x − 18 = 3 (x³− 4x² + 7x − 6) என இருப்பதால், தற்போது நாம்

 x³ − 5x² + 10x − 8 மற்றும் x³  − 4x² + 7x – 6 என்ற பல்லுறுப்புக் கோவைகளின் மீ.பொ.வ காண்போம்.

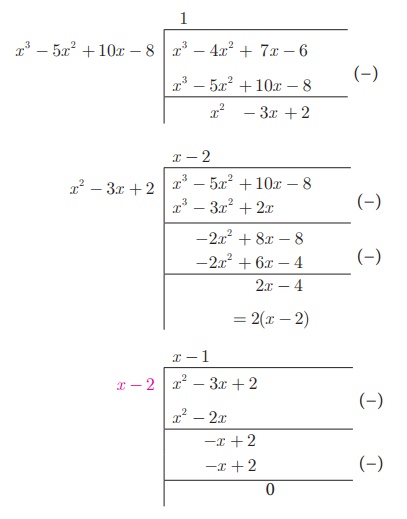
இங்கு, மீதி பூச்சியம் ஆகும். 

இங்கு தலையாயக் கெழுக்கள் 3 மற்றும் 6 -ன் மீ.பொ.வ 3 ஆகும். 

எனவே, மீ.பொ.வ [(6x 3 − 30x 2  + 60x − 48, 3x 3 − 12x 2  + 21x − 18)] = 3(x −2) .