தொகையீடு, பொருள், தொகையிடல் அடிப்படை விதிகள், பயன்பாடு, நுகர்வோர் உற்பத்தியாளர் உபரி - தொகை நுண்கணிதம் | 11th Economics : Chapter 12 : Mathematical Methods for Economics
11ஆம் வகுப்பு பொருளாதாரம் : இயல் 12 : பொருளியலுக்கான கணித முறைகள்
தொகை நுண்கணிதம்
தொகை நுண்கணிதம்
1. தொகையீடு
வகை நுண்கணிதம் சார்புகளின் மாற்ற வீதத்தை அளவிடுகிறது. அம்மாற்ற வீதங்கள் தரப்படின் F(x) என்ற சார்பினைக் காண்பதற்கு வகையிடலின் எதிர்மறை முறையும் பொருளியலில் தேவைப்படுகிறது. இதனை தொகையிடல் என்கிறோம். F(x) என்ற சார்பானது f(x) என்ற சார்பின் தொகையிடல் அல்லது எதிர் வகையிடல் என அழைக்கப்படுகிறது.
f(x) என்ற சார்பின் தொகையீட்டினை கணிதரீதியில்
∫f (x)dx = F(x)+C என குறிப்பிடலாம்.
சமன்பாட்டின் இடதுபுற பகுதியானது x ஐப் பொருத்து f(x) ஐ தொகையிட என குறிப்பிடப்படுகிறது. இங்கு, ∫என்பது தொகைக்குறியையும், f(x) என்பது தொகைப்படுத்த வேண்டிய சார்பினையும், C என்பது தொகையிடல் மாறிலியையும் F(x)+c என்பது வரையறைக்குட்படாத தொகையீட்டினையும் குறிக்கின்ற குறியீடுகளாகும். x சார்பு குறிப்பாக சொல்லப்படாததால் பல்வேறு மதிப்புகளை ஏற்க முடியும்.
2. பொருள்
F(x) ஐ x ஐப் பொருத்து வகையிட f(x) கிடைக்கும். எனவே f(x) ஐ x ஐப்பொருத்து தொகையிட F(x) கிடைக்கும். தொகையிடல் என்பது வகையிடலின் எதிர்மறை முறையாகும்.
குறியீட்டில்,
d[(F(x)] / dx = f (x), எனில்
∫f (x)dx = F (x)+C
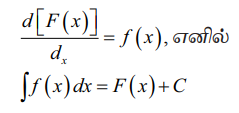
நினைவிற்கொள்ள வேண்டிய கருத்துக்கள்:
அ) தொகையிடல் என்பது ∫ என்ற குறியீட்டில் குறிப்பிடப்படுகிறது. அதாவது 'SUM' (தொகை) என்ற ஆங்கில வார்த்தையின் முதல் எழுத்தான S என்பதன் நீட்சி வடிவமாகும்.
ஆ) தொகைப்படுத்த வேண்டிய சார்பினை ஒட்டி வகையிடல் குறி 'dx' இடப்படுகிறது.
இ) f (x) dx = F(x)+C, C என்பது தொகையிடல் மாறிலியாகும். இங்கு ∫f(x) dx என்பதன் பொருள் x பொருத்து f(x)ஐதொகையிடல் ஆகும்.
3. தொகையிடல் அடிப்படை விதிகள் :
I) அடுக்கு விதி 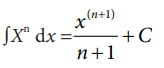
II) ∫ k.dx = x+c, இதில் K மாறிலி மதிப்பாகும்.
III) ∫ a.xn dx = a∫xn dx
எடுத்துக்காட்டு 12.22
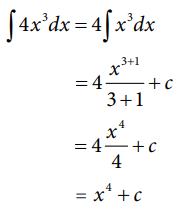
∫ 4x3dx = 4∫x3dx
= 4 x3+1 / 3 + 1 + C
= 4x4 / 4 + C
= x4 + C
எடுத்துக்காட்டு 12.23
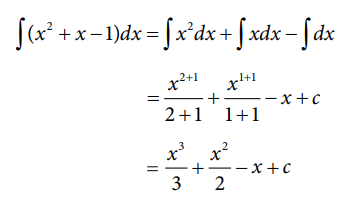
∫ (x2 +x-1) dx = ∫ x2dx + ∫ xdx - ∫ dx
= x2+1 / 2 + 1 + x1+1 / 1 + 1 – x + C
= x3 / 3 + x2 / 2 – x + C
எடுத்துக்காட்டு 12.24
∫ 5dx = 5x + c
எடுத்துக்காட்டு 12.25
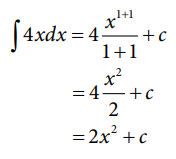
∫ 4xdx = 4 x 1+1 / 1 + 1 + C
= 4 x2 / 2 + C
= 2x2 +C
4. தொகையிடலின் பயன்பாடு
எடுத்துக்காட்டு 12.26
ஒரு நிறுவனத்தின் வெளியீடு x ஆக இருக்கும்போது அதன் இறுதிநிலை செலவுச்சார்பு 100–10x+0.1x2 என்க. அந்நிறுவனத்தின் மாறாச் செலவு ₹500 என்றால் மொத்தச் செலவுச் சார்பு காண்.
தீர்வு

MC = 100 – 10x + 0.1 x2
TC = ∫ (100 -10x + 0.1x2)dx
= 100x -10 x2 / 2 + 0.1 x3 / 3 + C
= 100x-5x2+ x3 / 30 + C
மாறாச் செலவு ₹500 தரப்பட்டுள்ளது.
∴ TC = 100x - 5x2 + x3 / 30 + 500
= x3 / 30 – 5x2 + 100x + 500
எடுத்துக்காட்டு 12.27
x அலகுகள் உற்பத்தி செய்வதற்கான இறுதிநிலை செலவுச்சார்பு y = 23 + 16x - 3x2 ஆகும். மேலும் பூஜ்ஜிய அலகு உற்பத்திக்கு மொத்தச் செலவு ₹40 ஆகின்றது. மொத்த செலவுச் சார்பினையும், சராசரி செலவுச் சார்பினையும் காண்க.
தீர்வு :
இறுதிநிலை செலவுச்சார்பு y = 23 + 16x - 3x2; c = 40 ஆகியன தரப்பட்டுள்ளன. மாறாச்செலவு ₹40 ஆகும்.
மாறாச்செலவு ₹40
மொத்த செலவுச்சார்பு = ∫ (இறுதிநிலை செலவுச்சார்பு) dx+c என அறிவோம்.
TC = ∫ ydx+c
= ∫ (23+16x-3x2) dx+c,
இங்கு c ஒரு மாறிலி
= ∫ 23dx + ∫ 16xdx - ∫ 3x2 dx+c
= 23x+16 [x2/ 2] – 3 [x3/ 3] + c
TC = 23x + 8x2 – x3 + C
c=40 என கொடுக்கப்பட்டுள்ளது
TC = 23x+8x2 - x3 + 40
சராசரி செலவுச்சார்பு = TC / x
= 23 + 8x - x2 + 40 / x
5. நுகர்வோர் உபரி
ஆல்ஃபிரட் மார்ஷல் இக்கோட்பாட்டினை விரிவாகத் தந்துள்ளார். குறிப்பிட்ட விலையில் மக்கள் பண்டங்களை வாங்கிடும் அளவிற்கான தொடர்பினை தேவைச்சார்பு P(X) காட்டுகிறது.
இதனை P = F (X) எனலாம்.
நுகர்வோர் உபரி என்பது ஒருவர் கொடுக்க நினைக்கும் விலைக்கும் உண்மையில் கொடுத்த விலைக்கும் இடையேயான வேறுபாடாகும்.
இதனை பின்வரும் வரைபடம் காட்டுகிறது.
நுகர்வோர் உபரி (CS) யினை கணிதரீதியில் பின்வருமாறு வரையறுக்கலாம்.
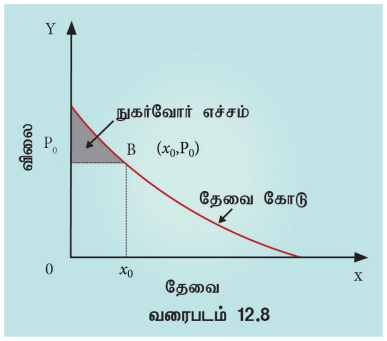
CS = (x = 0) முதல் x = x0 வரையிலான தேவை வளைகோட்டிற்கு உட்பட்ட பரப்பு) - (செவ்வகம் OX0BP0) யின் பரப்பு)
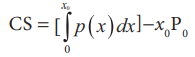
எடுத்துக்காட்டு 12.28
P = 35 - 2X - X2 ஆகவும் தேவை X0 என்பது 3 எனவும் அமையுமெனில் நுகர்வோர் உபரி என்ன ?
தீர்வு :
தரப்பட்ட தேவைச்சார்பு ,
P = 35 - 2x - x2
x = 3 எனில்,
P = 35 - 2(3) -32
= 35 - 6 - 9
P = 20
எனவே,
CS = (தேவை வளைக்கோட்டின் 0 முதல் 3 வரையிலான வளைக்கோட்டிற்கு கீழுள்ள பகுதியின் பரப்பு) - செவ்வகத்தின் பரப்பு (20 × 3 = 60)
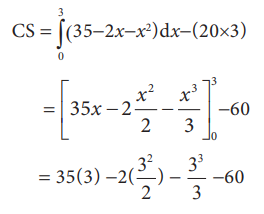
= 35(3) -2(32 / 2 ) - 33 / 3 - 60
= 105 -9 -9 - 60
= 27 அலகுகள்
6. உற்பத்தியாளர் உபரி:
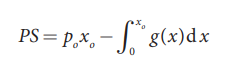
எடுத்துக்காட்டு 12.29
தேவைச்சார்பு PD = 25 – Q2 மற்றும் அளிப்புச்சார்பு PS = 2Q+1. ஆகியன தரப்பட்டுள்ளன.தூயபோட்டி நிலவும்போது (அ) நுகர்வோர் உபரி மற்றும் (ஆ) உற்பத்தியாளர் உபரி ஆகியவற்றைக் காண்க. (PD = தேவை விலை; PS = அளிப்பு விலை)
தீர்வு :
அங்காடி சமநிலையில், Pd = Ps
25-Q2 = 2Q+1
0 = -25 + Q2 + 2Q + 1
0 = -24 + Q2 + 2Q
Q2 + 2Q – 24 = 0
Q2 + 6Q - 4Q - 24 = 0
Q (Q + 6) -4(Q + 6) = 0
(Q+6)(Q- 4) = 0
எனவே, Q=4 அல்லது Q=-6. Q மதிப்பு -6 ஆக பொருளாதாரத்தில் பொருளற்றது. எனவே Q=4 ஆக இருக்கும்போது,
PD =25-42 = 9;
Ps = 2(4) + 1 = 9
நுகர்வோர் உபரி
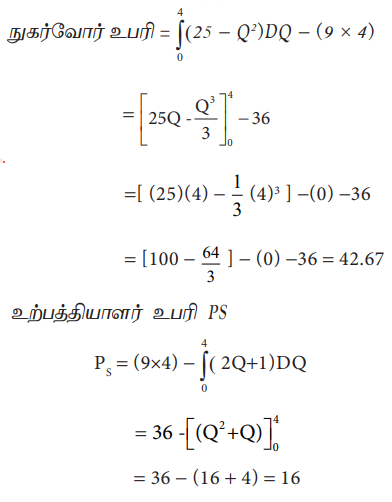
சிந்தித்து செயல்படு
• ஏதேனும் ஒரு பாடத்தில் கூடுதல் மணி நேரம் படிப்பதால் உனது மதிப்பெண்ணில் ஏற்படும் மாற்றத்தைக் காண்க.
• கூடுதல் அலகு கிமீ பயணிக்கும் போது பெட்ரோல் நுகர்வின் அளவினை காண்க.
• ஒவ்வொரு கூடுதல் அலகு கூலி அல்லது சம்பளம் அல்லது வருமானத்தை பொருத்து உனது பெற்றோரின் செலவழிப்பில் ஏற்படும் மாற்றம் குறித்துக் கேள்.