மீச்சிறு பொது மடங்கு (மீ.பொ.ம)

மீச்சிறு பொது மடங்கு (மீ.பொ.ம) (Least Common Multiple (LCM) of Polynomials)

இரண்டு அல்லது அதற்கு மேற்பட்ட பல்லுறுப்பு இயற்கணிதக் கோவைகளின் மீச்சிறு பொது மடங்கு ஆனது அவற்றால் வகுபடக் கூடிய மிகப்பெரிய படியைக் (அடுக்கை) கொண்ட கோவையாகும்.

பின்வரும் எளிய கோவைகளைக் கருதுவோம் a3b2,  a2b3.

இந்தக் கோவைகளின் மீ.பொ.ம = a3b3.

காரணிமுறையில் மீ.பொ.ம காண,

(i) முதலில் ஒவ்வொரு கோவையையும் அதன் காரணிகளாகப் பிரிக்கவும். 

(ii) அனைத்துக் காரணிகளின் மிக உயர்ந்த அடுக்கே மீ.பொ.ம ஆகும். (iii) கோவைகளில் எண் கெழுக்கள் இருக்குமானால் அவற்றுக்கு மீ.பொ.ம காண்க. 

(iv) எண்கெழுக்களின் மீ.பொ.ம மற்றும் கோவைகளின் மீ.பொ.ம ஆகியவற்றின் பெருக்கற்பலனே தேவையான மீ.பொ.ம ஆகும். 

எடுத்துக்காட்டு 3.12 

பின்வருவனவற்றிற்கு மீ.பொ.ம காண்க. 

(i) 8x4y2, 48x2y4

(ii) 5x -10, 5x2 – 20

(iii) x4 -1, x2 − 2x + 1

(iv) x3 - 27, (x - 3)2, x2 – 9

தீர்வு 

(i) 8x4y2, 48x 2y4 

முதலில் நாம் எண் கெழுக்களின் மீ.பொ.ம காண்போம். 

அதாவது, மீ.பொ.ம (8,48) = 2 × 2 × 2 × 6 = 48 

இப்போது உறுப்புகளில் உள்ள மாறிகளுக்கு மீ.பொ.ம காண்போம். அதாவது மீ.பொ.ம (x4y2, x2y4 )  = x4y4 

எண்கெழுக்களின் மீ.பொ.ம மற்றும் மாறிகளின் மீ.பொ.ம ஆகியவற்றின் பெருக்கற்பலன் கொடுக்கப்பட்ட கோவைகளின் மீ.பொ.ம ஆகும். எனவே, மீ.பொ.ம.

(8x4y2, 48x2y4) = 48x4y4

(ii) (5x -10), (5x 2 - 20)

5x -10 = 5(x − 2)

5x 2 - 20 = 5(x2 − 4) = 5(x + 2)(x − 2)

எனவே, மீ.பொ.ம [(5x − 10),(5x2 −20)] = 5(x + 2)(x −2)

(iii) (x4  -1),  x2 − 2x + 1

x4 - 1  = (x2)2 − 1 = (x2  + 1)(x2 − 1) = (x2  + 1)(x + 1)(x −1)

x2 − 2x + 1 = (x −1)2

எனவே, மீ.பொ.ம [(x4 − 1), (x2 − 2x + 1)] = (x2  + 1)(x + 1)(x −1)2

(iv) x3 - 27, (x - 3)2, x2 – 9

x3 - 27 = (x − 3) (x2 + 3x + 9) ; (x − 3)2  = (x − 3)2 ; (x 2 − 9) = (x + 3)(x − 3)

எனவே, மீ.பொ.ம [(x3 - 27), (x - 3)2, (x 2 - 9)] = (x − 3)2 (x + 3) (x2  + 3x + 9)

சிந்தனைக் களம் 

கொடுக்கப்பட்ட பல்லுறுப்புக்கோவைகள் f(x) மற்றும் g(x) ஆகியவற்றுக்கான காரணி மரத்தை நிறைவு செய்க. அதிலிருந்து அவற்றின் மீ.பொ.வ மற்றும் மீ.பொ.ம காண்க.

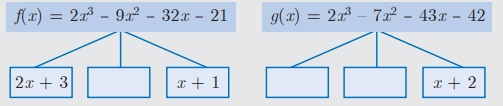
மீ.பொ.வ [f(x) மற்றும் g(x)] = ___ மீ.பொ.வ [f(x) மற்றும் g(x)] = ____