கோவை, பூச்சியங்கள், மூலங்கள், அமைத்தல், எடுத்துக்காட்டு, தீர்வு | இயற்கணிதம் - இருபடிச் சமன்பாடுகள் | 10th Mathematics : UNIT 3 : Algebra
10வது கணக்கு : அலகு 3 : இயற்கணிதம்
இருபடிச் சமன்பாடுகள்
இருபடிச் சமன்பாடுகள் (Quadratic Equations)
அறிமுகம்
லத்தீனில் ‘சவசோர்டா' எனும் பெயரால் அறியப்பட்ட கணிதவியலாளர் அப்ரஹாம் பார் ஹியா ஹா-நாசி என்பவர் பொ.யு 1145 ஆம் ஆண்டு 'லிபர் எம்படோரம்' எனும் புத்தகத்தை ஐரோப்பாவில் முதன்முதலில் வெளியிட்டார். இந்நூலில் இருபடிச் சமன்பாடுகளின் முழுமையான தீர்வுகள் குறிப்பிடப்பட்டுள்ளது.
மூவாயிரம் ஆண்டுகளுக்கு முற்பட்ட பண்டைய காலம் முதல் இன்றைய காலம் வரை இருபடிச் சமன்பாடுகளைத் தீர்க்கும் பல்வேறு வழிமுறைகளை மக்கள் அறிந்திருந்தனர். குறிப்பாக, சமன்பாட்டில் உள்ள கெழுக்கள், நான்கு அடிப்படைச் செயலிகள் மற்றும் வர்க்க மூலங்களைக் கொண்டு தீர்வைக் கண்டனர். இவ்வாறு பெறும் தீர்வு முறைகள் "படிமுறைத் தீர்வு” என அழைக்கப்படுகிறது. இன்று வரையில், பல்வேறு சமன்பாடுகளின் தீர்வைக் காண ஆழ்ந்த ஆய்வுகள் மேற்கொள்ளப்படுகின்றன.
இருபடிக் கோவை
a0xn+ a1xn−1+a2xn−2+ ... + an-1x + an என்பது x எனும் மாறியில் n படியில் அமைந்த கோவையாகும். மேலும், a0 ≠ 0 மற்றும் a1, a2, .... an ஆகியவை மெய் எண்கள். a0, a1, a2, .... an ஆகியவற்றை கெழுக்கள் என அழைக்கிறோம். குறிப்பாகக் கோவையின் படி 2 -ஆக இருப்பின் அதை ‘இருபடிக் கோவை' என அழைக்கிறோம். p(x) என்பது இருபடிக்கோவையெனில், அதை p(x) = ax2 + bx + c, என எழுதலாம். இங்கு, p(x) = ax2 + bx + c, a ≠ 0 மற்றும் a, b, c ஆகியவை மெய் எண்களாகும்.
1. இருபடி பல்லுறுப்புக் கோவையின் பூச்சியங்கள் (Zeroes of a Quadratic Polynomial)
p(x) என்பது ஒரு பல்லுறுப்பு கோவை என்க. p(a)=0 எனில் x=a என்பது p(x) - யின் ஒரு பூச்சியமாகும். எடுத்துக்காட்டாக, p(x) = x2–2x–8 எனில் p(-2) = 4 + 4 - 8 = 0 மற்றும் p(4) = 16 - 8 - 8 = 0. எனவே, -2 மற்றும் 4 என்பவை p(x) = x2 – 2x – 8. என்ற பல்லுறுப்புக் கோவையின் பூச்சியங்கள் ஆகும்.
2. இருபடிச் சமன்பாட்டின் மூலங்கள் (Roots of a Quadratic Equations)
ax2 + bx +c = 0, (a ≠ 0) என்பது ஓர் இருபடிச் சமன்பாடு என்க. ax2 + bx +c என்ற கோவையின் மதிப்பைப் பூச்சியமாக்குகின்ற x-யின் மதிப்புகளை ax2 + bx +c = 0 என்ற இருபடிச் சமன்பாட்டின் மூலங்கள் என்கிறோம்.
ax2 + bx +c = 0 என்க.

3. இருபடிச் சமன்பாட்டை அமைத்தல் (Formation of a Quadratic Equation)
α மற்றும் β என்பன ax2 + bx + c = 0 என்ற இருபடிச் சமன்பாட்டின் மூலங்கள் எனில்
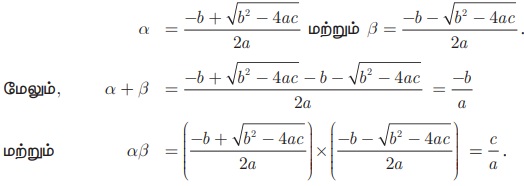
ஆகவே, (x - α) மற்றும் (x - β) என்பன ax2 + bx + c = 0 -யின் காரணிகள் ஆகும்.
(x - α) (x - β) = 0
எனவே, x 2 − (α + β) x + αβ = 0
அதாவது, x2 - (மூலங்களின் கூடுதல்) x + மூலங்களின் பெருக்கற்பலன் = 0. இதுவே கொடுக்கப்பட்ட இரு மூலங்களைக் கொண்ட இருபடிச் சமன்பாட்டின் பொதுவடிவம் ஆகும்.
குறிப்பு
ax2 + bx + c = 0 என்ற சமன்பாட்டை (a≠0) என்பதால் 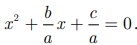 எனவும் எழுதலாம்.
எனவும் எழுதலாம்.
செயல்பாடு 2
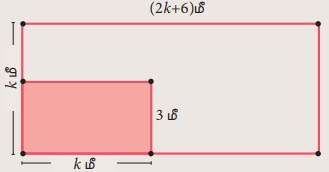
உன் வீட்டின் முன் (2k + 6) மீ மற்றும் k மீ அளவுகள் கொண்ட ஒரு செவ்வக வடிவப் பூங்கா உள்ளது என்க. படத்தில் உள்ளவாறு k மீ மற்றும் 3மீ அளவுகள் கொண்ட ஒரு சிறிய செவ்வகப் பகுதி சமன்படுத்தப்படுகிறது. மீதமுள்ள சமன்படுத்தப்படாத பூங்கா பகுதியின் பரப்பைக் காண்க.
எடுத்துக்காட்டு 3.23
x2 + 8x + 12 என்ற இருபடி கோவையின் பூச்சியங்களைக் காண்க.
தீர்வு
p(x) = x2 + 8x + 12 = (x+2) (x+6) என்க.
p(–2) = 4 – 16 + 12 = 0
p(–6) = 36 – 48 + 12=0
எனவே, p(x) = x2 + 8x + 12 -யின் பூச்சியங்கள் -2 மற்றும் -6 ஆகும்.
எடுத்துக்காட்டு 3.24
மூலங்களின் கூடுதல் மற்றும் பெருக்கல் கீழ்க்காணுமாறு கொடுக்கப்பட்டுள்ளன எனில், அவற்றுக்குத் தகுந்த இருபடிச் சமன்பாடுகளைக் கண்டறிக.
(i) 9, 14
(ii) – 7/2 , 5/2
(iii) – 3/5 , - 1/2
தீர்வு
(i) மூலங்கள் கொடுக்கப்பட்டால், இருபடிச் சமன்பாட்டின் பொது வடிவம்
x2 – (மூலங்களின் கூடுதல்) x + மூலங்களின் பெருக்கற்பலன் = 0
x2 − 9x + 14 = 0
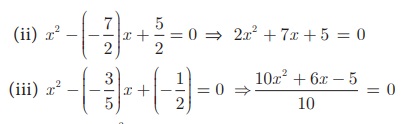
⇒ 10x2 + 6x − 5 = 0.
எடுத்துக்காட்டு 3.25
கீழேக் கொடுக்கப்பட்டுள்ள இருபடிச் சமன்பாடுகளின் மூலங்களின் கூடுதல் மற்றும் பெருக்கற்பலன் ஆகியவற்றைக் காண்க.
(i) x2 + 8x − 65 = 0
(ii) 2x2 + 5x + 7 = 0
(iii) kx2 − k2 x − 2k3 = 0
தீர்வு
α மற்றும் β என்பன கொடுக்கப்பட்ட இருபடிச் சமன்பாட்டின் மூலங்கள் என்க.
(i) x 2 + 8x − 65 = 0 இங்கு, a = 1, b = 8, c = –65
α + β = −b/a = –8 மற்றும் αβ = c/a = –65
α + β = −8 ; αβ = −65
(ii) 2x 2 + 5x + 7 = 0 இங்கு, a = 2, b = 5, c = 7
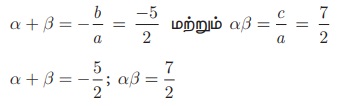
(iii) kx2 − k2 x − 2k3 = 0 இங்கு, a = k, b = -k2 , c = –2k3
