மூன்று மாறிகளில் அமைந்த நேரிய ஒருங்கமை சமன்பாடுகள்

மூன்று மாறிகளில் அமைந்த நேரிய ஒருங்கமை சமன்பாடுகள் (Simultaneous Linear Equations in Three Variables)

பல்பொருள் அங்காடியில் பல்வேறு பொருட்களை வாங்கும் போது மொத்தத் தொகையைக் கணக்கிடுவதில் தொடங்கி, சில குறிப்பிட்ட சூழல்களில் மனிதர்களின் வயதைக் கண்டறிதல், மேல்நோக்கி ஒரு குறிப்பிட்ட கோணத்தில் எறியப்பட்ட ஒரு பொருளின் பாதையைக் கணக்கிடுதல் வரை நம் அன்றாட வாழ்வில் பல்வேறு இடங்களில் இயற்கணிதம் முக்கியப் பங்காற்றுகிறது.

அண்டவெளியில் (Space) உள்ள எந்த ஒரு புள்ளியையும் அதன் அட்சரேகை, தீர்க்கரேகை மற்றும் உயர மதிப்புகளைக் கொண்டு சரியாகத் தீர்மானிக்கலாம். ஆகவே பூமியின் மீதுள்ள ஒரு புள்ளியின் அமைவிடத்தை அறிய, மூன்று செயற்கைக்கோள்கள் நிலைநிறுத்தப்பட்டு அதிலிருந்து மூன்று சமன்பாடுகள் பெறப்படுகின்றன. இந்த மூன்று சமன்பாடுகளில், இரு நேரிய சமன்பாடுகளும், ஓர் இருபடிச் சமன்பாடும் அடங்கும். ஆகவே, ஒரு குறிப்பிட்ட நேரத்தில் ஒரு பொருளின் அமைவிடத்தை சரியாக அறிய, நாம் அட்ச, தீர்க்க, உயர மாறிகளின் மதிப்பை, சமன்பாடுகளைத் தீர்ப்பதன் மூலம் அறியலாம். இதுவே, புவி நிலைப்படுத்துதல் அமைப்பின் (GPS - Geo Positioning System) அடிப்படையாகும். இதிலிருந்து, புவிநிலைப்படுத்துதல் அமைப்பில் மூன்று மாறிகளில் அமைந்த நேரிய ஒருங்கமை சமன்பாடுகள் பயன்படுவதைத் தெரிந்து கொள்ளலாம். 

1. மூன்று மாறிகளில் அமைந்த நேரிய சமன்பாடுகளின் தொகுப்பு (System of Linear equations in three variables)

நாம் முந்தைய வகுப்பில் இரு மாறிகளில் அமைந்த நேரிய ஒருங்கமை சமன்பாடுகளைத் தீர்ப்பதற்கான பல்வேறு முறைகளைக் கற்றோம். இங்கு நாம் x, y மற்றும் z என்ற மூன்று மாறிகளில் அமைந்த நேரிய சமன்பாட்டு தொகுப்பிற்குத் தீர்வு காண்போம். x, y, z என்ற மூன்று மாறிகளில் அமைந்த நேரிய சமன்பாட்டின் பொது வடிவம் ax + by + cz + d = 0, இங்கு a, b, c, d என்பன மெய்யெண்கள் மற்றும் a, b, c என்பனவற்றில் ஏதேனும் ஒன்றாவது பூச்சியமற்றதாக இருக்கும்.

குறிப்பு 

ax + by + c = 0, என்ற வடிவில் இரு மாறிகளில் அமைந்த நேரிய சமன்பாடு ஒரு நேர்க்கோட்டைக் குறிக்கும்.

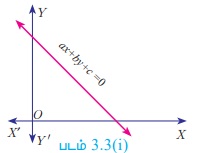
ax + by + cz + d = 0, என்ற வடிவில் மூன்று மாறிகளில் அமைந்த நேரிய சமன்பாடு ஒரு தளத்தைக் குறிக்கும்.

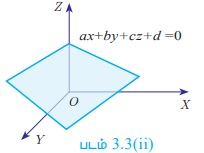
பொது வடிவம்: x, y, z என்ற மூன்று மாறிகளில் அமைந்த நேரிய சமன்பாட்டு தொகுப்பின் பொதுவடிவம்

a1x + b1y +c1z + d1 = 0

a2 x + b2y +c2 z + d2 = 0

a3 x + b3y +c3 z + d3 = 0

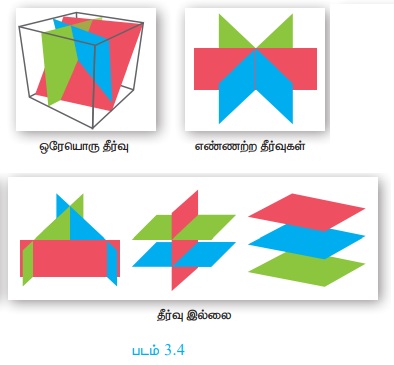
இச்சமன்பாட்டு தொகுப்பில் உள்ள ஒவ்வொரு சமன்பாடும் முப்பரிமாண வெளியில் ஒரு தளத்தைக் குறிக்கும். இந்த மூன்று சமன்பாடுகளால் வரையறுக்கப்படும் மூன்று தளங்களும் சந்திக்கும் புள்ளியோ அல்லது பகுதியோ இந்தச் சமன்பாட்டு தொகுப்பின் தீர்வாகும். மூன்று மாறிகளில் அமைந்த நேரிய சமன்பாட்டு தொகுப்பிற்கு, அவை குறிக்கும் தளங்கள் ஒவ்வொன்றும் மற்றவற்றை எவ்வாறு வெட்டுகின்றன என்பதைப் பொறுத்து ஒரேயொரு தீர்வு, எண்ணற்ற தீர்வுகள், தீர்வு இல்லை என்ற வகையில் தீர்வுகள் அமையும்.

பின்வரும் படங்கள் தீர்வுகளின் வாய்ப்புகளை விளக்குவதாக அமைந்துள்ளன.

மூன்று மாறிகளில் அமைந்த நேரிய சமன்பாட்டு தொகுப்பிற்குத் தீர்வு காணும் படிநிலைகள் 

படி 1 கொடுக்கப்பட்ட மூன்று சமன்பாடுகளில் ஏதேனும் இரண்டு சமன்பாடுகளை எடுத்து, பொருத்தமான பூச்சியமற்ற மாறிலியால் பெருக்கி அவற்றில் ஏதேனும் ஒரு மாறியின் கெழுக்களைச் சமப்படுத்துக. 

படி 2 சமன்பாடுகளைக் கழித்துக் கெழுக்கள் சமமாக உள்ள மாறியை நீக்குக. 

படி 3 வேறு ஒரு சோடி சமன்பாடுகளை எடுத்து அதே மாறியை நீக்குக. 

படி 4 தற்போது நாம் இரு மாறிகளில் அமைந்த இரு சமன்பாடுகளைப் பெறுவோம். 

படி 5 இச்சமன்பாடுகளை முந்தைய வகுப்பில் கற்ற முறைகளைப் பயன்படுத்தித் தீர்க்க. 

படி 6 மேற்கண்ட படியில் கிடைத்த இரு மாறிகளின் தீர்வை ஏதேனும் ஒரு சமன்பாட்டில் பிரதியிட மூன்றாவது மாறியின் மதிப்பைப் பெறலாம்.

குறிப்பு 

• மேற்கண்ட படிநிலைகளில் 0 = 1 என்பது போன்ற தவறான முடிவு கிடைக்குமாயின் அந்தச் சமன்பாட்டு தொகுப்பிற்குத் தீர்வு இல்லை. 

• தவறான சமன்பாடுகள் கிடைக்காமல், 0 = 0 என்பது போன்ற முற்றொருமை கிடைக்குமாயின் அந்தச் சமன்பாட்டு தொகுப்பிற்கு எண்ணற்ற தீர்வுகள் இருக்கும்.

எடுத்துக்காட்டு 3.3 

பின்வரும் மூன்று மாறிகளில் அமைந்த நேரிய சமன்பாட்டு தொகுப்பினைத் தீர்க்க. 

3x – 2y + z =2, 2x + 3y – z = 5 , x + y + z = 6 . 

தீர்வு 

3x − 2y + z = 2                             …(1)

2x + 3y – z = 5                              …(2)

x + y + z = 6                                  …(3)

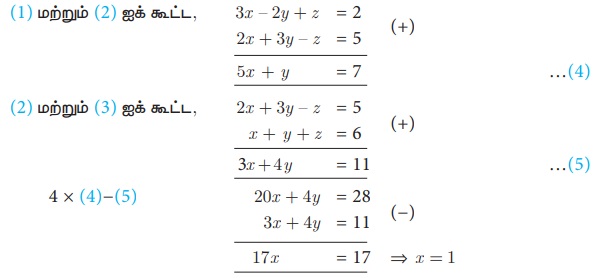
x = 1 என (4) -யில் பிரதியிட, 5 + y =7 ⇒ y = 2

x = 1, y = 2 என (3) -யில் பிரதியிட, 1 + 2 + z = 6 ⇒ z = 3 

எனவே, x = 1, y = 2, z = 3

எடுத்துக்காட்டு 3.4 

பள்ளிகளுக்கிடையேயான ஒரு தடகளப் போட்டியில், மொத்த பரிசுகள் 24 கொண்ட தனிநபர் போட்டிகளில் ஒட்டுமொத்தமாக 56 புள்ளிகள் ஒதுக்கப்பட்டுள்ளது. முதலிடம் பெறுபவருக்கு 5 புள்ளிகளும், இரண்டாமிடம் பெறுபவருக்கு 3 புள்ளிகளும், மூன்றாமிடம் பெறுபவருக்கு 1 புள்ளியும் அளிக்கப்படும். மூன்றாமிடம் பெற்றவர்களின் எண்ணிக்கை முதல் மற்றும் இரண்டாம் இடங்களைப் பிடித்தவர்களின் எண்ணிக்கையின் கூடுதலுக்குச் சமம் எனில், முதல், இரண்டாம் மற்றும் மூன்றாமிடம் பெற்றவர்களின் எண்ணிக்கையைக் காண்க. 

தீர்வு 

முதலிடம் பெறுபவர்களின் எண்ணிக்கை x, இரண்டாமிடம் பெறுபவர்களின் எண்ணிக்கை y, மூன்றாமிடம் பெறுபவர்களின் எண்ணிக்கை z என்க.

மொத்தப் போட்டிகள் = 24; மொத்த புள்ளிகள் = 56. 

எனவே, மூன்று மாறிகளில் அமைந்த நேரிய சமன்பாடுகள்

x + y + z = 24 …(1)

5x + 3y + z = 56 …(2)

x + y = z  …(3)

(3) ஐ (1) -யில் பிரதியிட, நாம் பெறுவது, z + z = 24 ⇒ z = 12 

எனவே, (3) ⇒ x + y = 12

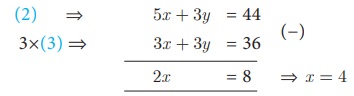
x = 4, z = 12 என (3) -யில் பிரதியிட நாம் பெறுவது, y = 12 – 4 = 8

எனவே, முதலிடம் பெற்றவர்களின் எண்ணிக்கை 4 ஆகும்;

இரண்டாமிடம் பெற்றவர்களின் எண்ணிக்கை 8 ஆகும்; 

மூன்றாமிடம் பெற்றவர்களின் எண்ணிக்கை 12 ஆகும்;

எடுத்துக்காட்டு 3.5 

தீர்க்க 

x + 2y – z = 5; x − y + z = −2; − 5x − 4y + z = −11

தீர்வு 

x + 2y – z = 5 …(1) 

x – y + z = –2 …(2)

–5x –4y + z = –11 …(3)

இங்கு 0 = 0 என்ற முற்றொருமை கிடைக்கிறது.

எனவே, கொடுக்கப்பட்ட சமன்பாட்டு தொகுப்பிற்கு எண்ணற்ற தீர்வுகள் உண்டு.

எடுத்துக்காட்டு 3.6

தீர்க்க 3x + y – 3z = 1; –2x – y + 2z = 1 ; –x – y + z = 2 .

தீர்வு 

3x + y − 3z = 1 … (1)

− 2x −y + 2z = 1  … (2)

−x − y + z = 2   … (3)

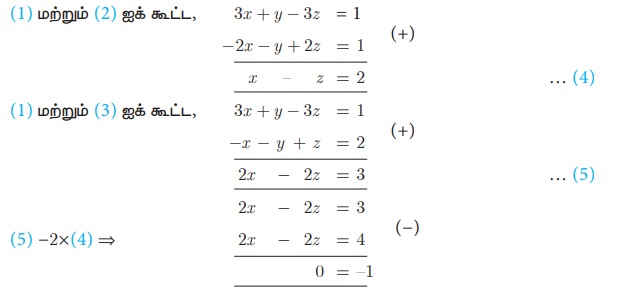
இங்கு நாம் 0 = -1 என்ற தவறான முடிவைப் பெறுகிறோம். எனவே, இந்தத் தொகுப்பானது ஒருங்கமைவற்றது. மேலும் கொடுக்கப்பட்ட சமன்பாட்டு தொகுப்பிற்குத் தீர்வு இல்லை.

எடுத்துக்காட்டு 3.7 

தீர்க்க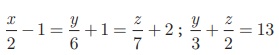

தீர்வு

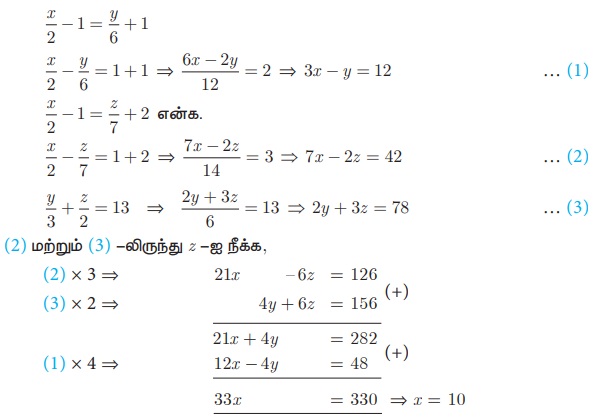
x = 10 என (1) -யில் பிரதியிட, 30 − y = 12 ⇒ y = 18 

x = 10 என (2) - யில் பிரதியிட, 70 − 2z = 42 ⇒ z = 14 

எனவே, x = 10, y = 18, z = 14.

எடுத்துக்காட்டு 3.8 

தீர்க்க: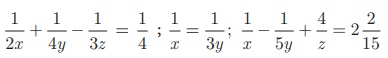

தீர்வு 

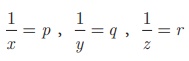என்க.

கொடுக்கப்பட்ட சமன்பாடுகளை

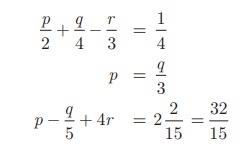என எழுதலாம்.

இவற்றைச் சுருக்கும்போது கிடைப்பது,

6p + 3q − 4r = 3                    …(1)

3p = q                           …(2)

15p − 3q + 60r = 32   …(3)

(2) -ஐ (1) மற்றும் (3) - யில் பிரதியிட நாம் பெறுவது,

15p - 4r = 3               …(4)

6p + 60r = 32 ⇒ 3p + 30r  = 16  …(5) 

(4) மற்றும் (5) - ஐத் தீர்க்க

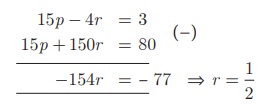
r = 1/2 என (4) -யில் பிரதியிட நமக்குக் கிடைப்பது, 15p - 2 = 3 ⇒ p = 1/3

(2) ⇒ q = 3p ⇒ q = 1

எனவே, x = 1/p = 3,  y = 1/q = 1, z = 1/r = 2 . அதாவது, x = 3, y = 1, z = 2 .

எடுத்துக்காட்டு 3.9 

முதல் எண்ணின் மும்மடங்கு, இரண்டாம் எண் மற்றும் மூன்றாம் எண்ணின் இரு மடங்கு ஆகியவற்றின் கூடுதல் 5. முதல் எண் மற்றும் மூன்றாம் எண்ணின் மும்மடங்கு ஆகியவற்றின் கூடுதலிலிருந்து இரண்டாம் எண்ணின் மும்மடங்கைக் கழிக்க நாம் பெறுவது 2. முதல் எண்ணின் இரு மடங்கு மற்றும் இரண்டாம் எண்ணின் மும்மடங்கு ஆகியவற்றின் கூடுதலிலிருந்து மூன்றாம் எண்ணைக் கழிக்க நாம் பெறுவது 1. இவ்வாறு அமைந்த மூன்று எண்களைக் காண்க. 

தீர்வு 

தேவையான மூன்று எண்கள் x, y, z என்க.

கொடுக்கப்பட்ட விவரங்களிலிருந்து நாம் பெறுவது, 

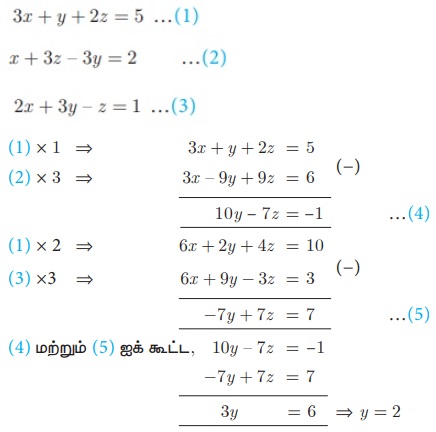
y = 2 என (5) -யில் பிரதியிட, − 14 + 7z = 7 ⇒ z = 3

y = 2 என z = 3, (1) -யில் பிரதியிட,

3x + 2 + 6 = 5 ⇒ x = −1

எனவே, தேவையான எண்கள் x = –1, y = 2, z = 3.

சிந்தனைக் களம் 

1. மூன்று மாறிகளில் அமைந்த ஒரு நேரிய சமன்பாட்டு தொகுப்பினைத் தீர்க்கும்போது கிடைக்கும் தீர்வுகளின் எண்ணிக்கை __________ 

2. மூன்று தளங்கள் இணையாக இருப்பின் அவை சந்திக்கும் புள்ளிகளின் எண்ணிக்கை _______________

முன்னேற்றச் சோதனை

1. மூன்று மாறிகளில் அமைந்த நேரிய சமன்பாட்டு தொகுப்பிற்கு ஒரேயொரு தீர்வு கிடைக்க வேண்டுமெனில் தேவைப்படும் குறைந்தபட்ச சமன்பாடுகளின் எண்ணிக்கை _______________

2. ___________ எனில், நேரிய சமன்பாட்டு தொகுப்பு ஒரு முற்றொருமையைக் கொடுக்கும். 

3. __________ எனில், நேரிய சமன்பாட்டு தொகுப்பின் முடிவு பொருளற்றது.