இருபடிச் சமன்பாட்டின் மூலங்களுக்கும் கெழுக்களுக்கும் இடையேயுள்ள தொடர்பு

இருபடிச் சமன்பாட்டின் மூலங்களுக்கும் கெழுக்களுக்கும் இடையேயுள்ள தொடர்பு (The Relation between Roots and Coefficient of a Quadratic Equation)

ax2 + bx +c = 0 எனும் இருபடிச் சமன்பாட்டின் மூலங்கள் α மற்றும் β எனில்,

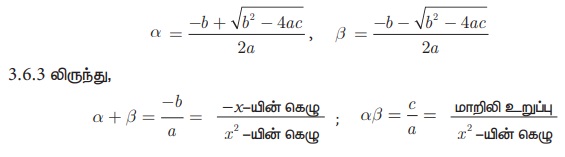
முன்னேற்றச் சோதனை

எடுத்துக்காட்டு 3.43 

x2 − 13x + k = 0 என்ற சமன்பாட்டின் மூலங்களின் வித்தியாசம் 17 எனில், k-யின் மதிப்புக் காண்க. 

தீர்வு 

x2 − 13x + k = 0 இங்கு, a = 1, b = −13, c = k 

α, மற்றும் β சமன்பாட்டின் மூலங்கள் என்க.

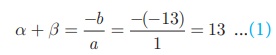
α – β = 17 ….(2) (கொடுக்கப்பட்டது)

(1) + (2) ⇒ 2 α = 30 எனவே, α = 15

α = 15 ஐ (1)-யில் பிரதியிட, 

15 + β = 13 ⇒ β = -2 

ஆனால், (2) ⇒ αβ = c/a = k/1 ⇒ 15 × (−2) = k எனவே, k = −30 

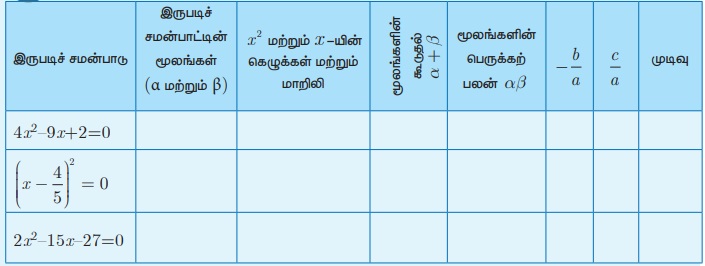
சிந்தனைக் களம்

ax2 − bx + c = 0 என்ற இருப்படி சமன்பாட்டில் நிலைத்த மதிப்பு 0 வாக இருந்தால் இதன் மூலங்களின் கூடுதல் மற்றும் பெருக்கற்பலன் --------- மற்றும் ------------ ஆகும்.

எடுத்துக்காட்டு 3.44 

x2 + 7 x + 10 = 0 எனும் சமன்பாட்டின் மூலங்கள் α மற்றும் β  எனில், பின்வருவனவற்றின் மதிப்புகளைக் காண்க. 

(i) (α - β)

(ii) α2 + β2

(iii) α3 - β3

(iv) α4 + β4

(v) α/β  + β/α

(vi) α2/ β  + β2/α

தீர்வு 

x2 + 7 x + 10 = 0 இங்கு, a = 1, b = 7, c =10 

α மற்றும் β சமன்பாட்டின் மூலங்கள் எனில்,

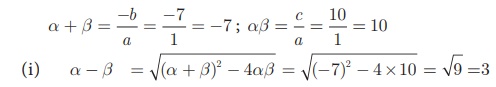
(ii) α2 + β2 = (α + β)2 − 2αβ = (−7)2 − 2 × 10 = 29

(iii) α3 - β3 = (α − β)3 + 3αβ (α − β) = (3)3  + 3(10)(3) =117

(iv) α4 + β4 = (α 2 + β2)2 − 2α2 β2 

((ii)-லிருந்து, α 2 + β2 = 29 எனவே, 292 – 2 × (10)2 = 641 

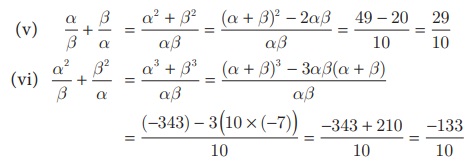
எடுத்துக்காட்டு 3.45 

3x2 + 7 x − 2 = 0 என்ற சமன்பாட்டின் மூலங்கள் α மற்றும் β எனில் கொடுக்கப்பட்ட மதிப்புகளைக் காண்க.

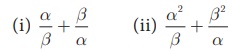
தீர்வு 

3x2 + 7 x − 2 = 0 இங்கு, a = 3, b = 7 , c = −2

α, β சமன்பாட்டின் மூலங்கள்; எனவே,

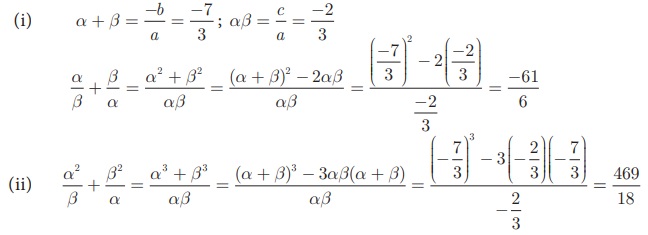
எடுத்துக்காட்டு 3.46 

2x2 − x −1 = 0 என்ற சமன்பாட்டின் மூலங்கள் α மற்றும் β எனில், கீழே கொடுக்கப்பட்ட மூலங்களையுடைய இருபடிச் சமன்பாட்டைக் காண்க.

(i) 1/α, 1/β

(ii) α 2β, β 2α

(iii) 2α + β, 2β + α

தீர்வு 

2x2 − x −1 = 0 இங்கு, a = 2 , b = −1 , c = −1 

α + β = −b/a = −(−1) / 2 = 1/2 ; αβ = c/a = −1/2

(i) கொடுக்கப்பட்ட மூலங்கள் 1/α , 1/β

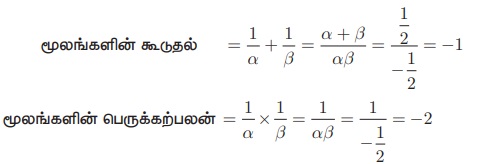
தேவையான சமன்பாடு, x2 - (மூலங்களின் கூடுதல்) x + (மூலங்களின் பெருக்கற்பலன்) = 0

x 2 − (−1)x − 2 = 0 ⇒ x2 + x − 2 = 0 

(ii) கொடுக்கப்பட்ட மூலங்கள் α2 β, β2 α 

மூலங்களின் கூடுதல் α2β + β2α = αβ(α+β) = -1/2(1/2) = -1/4 

மூலங்களின் பெருக்கற்பலன் (α2β) × (β2α) = α3β3 = (αβ)3 = (-1/2)3 = -1/8

தேவையான சமன்பாடு, x2 - (மூலங்களின் கூடுதல்) x + (மூலங்களின் பெருக்கற்பலன்) = 0

 x2 – (-1/4) x – 1/8 = 0 ⇒ 8x2 + 2x – 1 = 0

(iii) 2α + β, 2β + α

மூலங்களின் கூடுதல் 2α + β + 2β + α = 3(α + β) = 3(1/2) = 3/2

மூலங்களின் பெருக்கற்பலன் = (2α + β) (2β + α) = 4αβ + 2α 2 + 2β2 + αβ

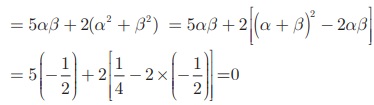
தேவையான சமன்பாடு, x2 – (மூலங்களின் கூடுதல்) x + (மூலங்களின் பெருக்கற்பலன்) = 0

x2 – 3/2 x + 0 = 0 ⇒ 2x2 − 3x = 0.