எண்ணுதலின் அடிப்படைக் கொள்கைகள்

எண்ணுதலின் அடிப்படைக் கொள்கைகள் (Fundamental Principles of Counting)

1. கூட்டல் விதி: (Sum Rule) செய்து முடிக்க வேண்டிய இரண்டு பணிகளை எடுத்துக்கொள்வோம். ஒரே நேரத்தில் செய்ய இயலாத இரண்டு பணிகளில் முதல் பணியினை M வழிகளிலும், இரண்டாவது பணியினை N வழிகளிலும் செய்யலாம் எனில், இவற்றில் ஏதேனும் ஒரு பணியினை M + N வழிகளில் செய்யலாம். இதனை எண்ணுதலின் கூட்டல் விதி என்கிறோம்.

எடுத்துக்காட்டு 4.1 17 மாணவர்கள், 29 மாணவிகள் உள்ள வகுப்பிலிருந்து ஒரு போட்டிக்காக ஒரு மாணவியையோ அல்லது மாணவனையோ எத்தனை வேறுபட்ட வழிகளில் தேர்ந்தெடுக்க முடியும்?

தீர்வு:

முதல் செயலான ஒரு மாணவியை தேர்ந்தெடுக்க 29 வழிகளும், இரண்டாவது செயலான ஒரு மாணவனை தேர்ந்தெடுக்க 17 வழிகளும் உள்ளன. எனவே இந்த தேர்வினை செய்ய எண்ணுதலின் கூட்டல் விதியின்படி, 17 + 29 = 46 வழிகள் உள்ளன.

குறிப்பு: இந்த விதியினை இரண்டிற்கு மேலான பணிகளுக்கும் விரிவுபடுத்தலாம். ஆகவே ஒரே நேரத்தில் செய்ய இயலாத n பணிகள் T1, T2, T3....., Tn ஆகியவற்றை செய்து முடிக்க முறையே m1,, m2...., mn வழிகள் உள்ளன எனில், இவற்றில் ஏதேனும் ஒன்றை m1 + m2 +... + mn வழிகளில் செய்யலாம்.

2. பெருக்கல் விதி : (Product Rule) ஒரு செயலை செய்ய இரு படி நிலைகள் உள்ளன எனக் கொள்க. முதல் படி நிலையை செய்ய M வெவ்வேறான வழிகளும் முதல் படி நிலையை செய்து முடித்தபின் இரண்டாவது படி நிலையைச் செய்ய N வெவ்வேறான வழிகளும் உள்ளன எனில், மொத்தமாக அந்த செயலை M × N வழிகளில் செய்து முடிக்க முடியும்.

எடுத்துக்காட்டு 4.2 சென்னை, திருச்சி மற்றும் திருநெல்வேலி என்ற மூன்று நகரங்களை எடுத்துக்கொள்வோம். ஒருவர் சென்னையிலிருந்து திருச்சி வழியாகத்தான் திருநெல்வேலி செல்ல முடியும் என்க. சென்னை மற்றும் திருச்சிக்கு இடையே 2 சாலைகளும், திருச்சியிலிருந்து திருநெல்வேலி செல்ல 3 சாலைகளும் உள்ளன. சென்னையிலிருந்து திருநெல்வேலிக்கு எத்தனை வழிகளில் செல்ல முடியும்?

தீர்வு: 

சென்னையிலிருந்து திருச்சி செல்ல 2 சாலைகள் உள்ளன. இவற்றை R1 மற்றும் R2 எனக் கொள்க. மேலும் திருச்சியிலிருந்து திருநெல்வேலி செல்ல 3 சாலைகள் உள்ளன. இவற்றை S1, S2 மற்றும் S3 எனக் கொள்க. ஒருவர் சென்னையிலிருந்து திருச்சி செல்ல R1 ஐ தேர்ந்தெடுத்தால் திருச்சியிலிருந்து திருநெல்வேலி செல்ல S1, S2 அல்லது S3 இல் ஏதேனும் ஒன்றைத் தேர்வு செய்யலாம். எனவே (R1, S1), (R1, S2), (R1, S3) என்ற சாத்தியமான சாலை வழிகள் உள்ளன. இதுபோலவே, சென்னையிலிருந்து திருச்சி செல்ல R2 வை தேர்ந்தெடுத்தால் (R2, S1,), (R2, S2), (R2, S3) என்ற சாத்தியமான சாலை வழிகள் உள்ளன.

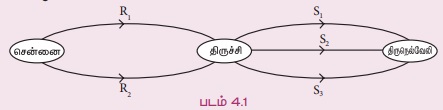
எனவே, சென்னையிலிருந்து திருநெல்வேலி செல்ல 2 × 3 = 6 வழிகள் உள்ளன.

குறிப்பு: இதனை இரண்டிற்கு மேலான படி நிலைகளுக்கும் விரிவுபடுத்தலாம். ஒரு செயலில் உள்ள P1, P2..., Pn என்ற n படிநிலைகளை செய்ய முறையே m1, m2.,..., mn என்ற வழிகள் உள்ளன என்க. மேலும், P1, P2,...., Pi-1 படி நிலைகளுக்கு பிறகு Pi என்ற படிநிலையை செய்தால், அந்த செயலை m1 × m2 × .... ×mn வழிகளில் செய்யலாம்.

3. சேர்த்தல் - நீக்கல் கொள்கை: (The Inclusion - Ereclution Principle) A, B என்ற இரு பணிகளை ஒரே நேரத்தில் செய்வதாகக் கொள்வோம். ஒவ்வொன்றையும் தனித்தனியே முறையே n(A), n(B) வழிகளில் செய்யலாம் எனக் கொள்க. மேலும் A, B ஆகியவற்றை ஒரே நேரத்தில் சேர்த்து n(A ∩ B) வழிகளில் செய்யலாம் எனில், இவற்றில் ஏதேனும் ஒரு பணியை செய்யும் வழிகளின் எண்ணிக்கையை காண கூட்டல் விதியைப் பயன்படுத்தினால் அது உண்மையில் உள்ளதைவிட அதிக எண்ணிக்கையை கொடுக்கும். சரியான விடையை பெற இவ்விரு பணிகளைச் செய்யும் வழிகளின் எண்ணிக்கையை கூட்டிய பின்னர், இரண்டு பணிகளையும் ஒரே நேரத்தில் சேர்த்து செய்யும் வழிகளின் எண்ணிக்கையை கழிக்க வேண்டும். இந்த முறையை சேர்த்தல் - நீக்கல் கொள்கை என்கிறோம். கணங்களின் குறியீட்டால் இதனை கீழ்க்கண்டவாறு குறிக்கின்றோம்.

n(A ∪ B) = n(A) + n(B) − n(A ∩ B).

1000 வரை உள்ள மிகை முழு எண்களில் 2 அல்லது 7 ஆல் வகுபடும் (ஆனால், இவ்விரு எண்களால் வகுபடும் எண்களைத் தவிர்த்து) எண்களை காண்பதாக கொள்வோம். 2 ஆல் வகுபடும் எண்களின் எண்ணிக்கையை n(A) எனவும், 7 ஆல் வகுபடும் எண்களின் எண்ணிக்கையை n(B) எனவும் 2 மற்றும் 7 ஆல் வகுபடும் எண்களின் எண்ணிக்கையை n(A ∩ B) எனவும் கொள்க. 2 அல்லது 7 ஆல் வகுபடும் மிகை முழு எண்களின் எண்ணிக்கை

n(A ∪ B) = n(A) + n(B) − n(A ∩ B) = 500 + 142 − 71 = 571. 

(குறிப்பு: இங்கு 1000 வரை உள்ள எல்லா 2-ன் மடங்குகளின் எண்ணிக்கையை n(A) எனவும், எல்லா 7-ன் மடங்குகளின் எண்ணிக்கையை n(B) எனவும் மேலும் இவ்வாறாகப் பலவற்றிற்கும் தொடரலாம்.)

மர வரைபடங்கள்:

மர வரைபடங்கள் பெரும்பாலும் எண்ணுதலுக்கான பல்வேறு வாய்ப்புகளை குறிக்க பயன்படுகிறது. மரத்தில் உள்ள கிளைகள் பல்வேறு வாய்ப்புகளை குறிக்கிறது. உதாரணமாக, ஒருவர் தன் குடும்பத்திற்காக ஒரு மகிழுந்தை வாங்குவதாக கொள்வோம். இரண்டு வெவ்வேறான வியாபார முத்திரை (Branded) மகிழுந்துகளும் ஒவ்வொரு வியாபார முத்திரையிலும் 5 நிறங்களில் மகிழுந்துகளும் உள்ளன. மேலும், ஒவ்வொரு நிறத்திலும் GL, SS, SL என மூன்று வகைகள் உள்ளன எனில், ஒரு மகிழுந்தை தேர்ந்தெடுப்பதற்கான பல்வேறு வாய்ப்புகளை மர வரைபடம் வாயிலாக கீழ்க்காணுமாறு குறிக்கலாம்.

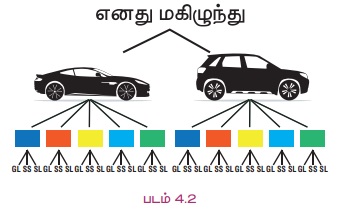
நாம் இப்பொழுது மேற்கூறிய விதிகளை எடுத்துக்காட்டுகளின் மூலம் விரிவாக விளக்குவோம்.

எடுத்துக்காட்டு 4.3 ஒரு பள்ளி நூலகத்தில் 75 கணிதப் புத்தகங்களும், 35 இயற்பியல் புத்தகங்களும் உள்ளன. ஒரு மாணவன் இதில் ஏதேனும் ஒரே ஒரு புத்தகத்தை தேர்ந்தெடுக்கலாம். கணிதம் அல்லது இயற்பியல் புத்தகங்களில் ஏதாவது ஒன்றை எத்தனை வழிகளில் அம்மாணவனால் தேர்ந்தெடுக்க முடியும்? 

தீர்வு:

(i) கணிதப் புத்தகத்தைத் தேர்ந்தெடுக்க 75 வழிகள் உள்ளன.

(ii) இயற்பியல் புத்தகத்தைத் தேர்ந்தெடுக்க 35 வழிகள் உள்ளன.

எனவே, கணிதம் அல்லது இயற்பியல் புத்தகங்களில் ஏதேனும் ஒன்றை தேர்ந்தெடுக்க கூட்டல் விதிப்படி 75 + 35 = 110 வழிகள் உள்ளன.

நாம், இப்பொழுது பாட அறிமுகத்தில் விவரித்ததுபோன்ற போன்ற கணக்கினைக் காண்போம்.

எடுத்துக்காட்டு 4.4 ஒரு மின் நுகர்வோரின் மின் அட்டை எண் 238 : 110 : 29 என உள்ளது. 238 வது அதிக மின் திறன் கொண்ட மின் மாற்றியில் இந்த 29 வது நுகர்வோர் எண் வரை உள்ள மின் இணைப்புகளின் எண்ணிக்கையை குறைந்த மின் திறனுடைய மின்மாற்றியில் அதிகப்பட்சம் 100 மின் இணைப்புகள் மட்டுமே இணைக்க முடியும் என்ற நிபந்தனைக்குட்பட்டு காண்க.

தீர்வு :

படமானது மின் வழங்கல் வலைப்பின்னல் முறையை விளக்குகிறது.

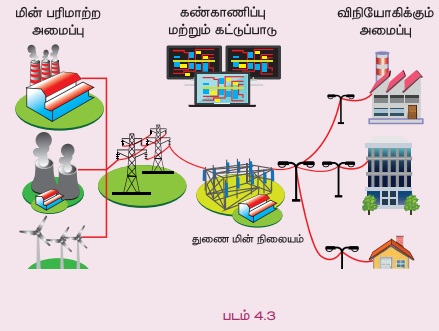
இங்கு 110 குறைந்த மின் திறனுடைய மின் மாற்றிகள் அதிக மின் திறனுடைய மின்மாற்றியுடன் இணைக்கப்பட்டுள்ளது. ஒவ்வொரு குறைந்த மின் திறனுடைய மின் மாற்றியுடனும் 100 நுகர்வோர்கள் இணைக்கப்பட்டுள்ளதால், 109 மின்மாற்றிகளுக்கு மொத்தம் 109 × 100 = 10900 இணைப்புகள் இருக்கும். 110 வது மின்மாற்றியில் 29 நுகர்வோர்கள் இணைக்கப்பட்டுள்ளனர். எனவே, 238 வது அதிக மின் திறன் கொண்ட மின்மாற்றியில் மொத்தம் 10900 + 29 = 10929 மின் இணைப்புகள் இருக்கும்.

எடுத்துக்காட்டு 4.5 ஒரு நபர் ஒரு மகிழுந்து வாங்க விரும்புகிறார், சந்தையில் இரண்டு வகையான வியாபார முத்திரை மகிழுந்துகள் உள்ளன. மேலும் ஒவ்வொரு வியாபார முத்திரை மகிழுந்திலும் 3 வெவ்வேறு வகைகள் உள்ளன. மேலும் இந்த ஒவ்வொரு வகையிலும் படம் 4.2 இல் உள்ளது போல் 5 வெவ்வேறு நிறங்களில் மகிழுந்துகள் வருகின்றன. எத்தனை வழிகளில் மகிழுந்துகளை அவரால் தேர்ந்தெடுக்க முடியும்?

தீர்வு:

ஒரு மகிழுந்து வாங்க ஒரு வியாபார முத்திரை, ஒரு வகை மற்றும் ஒரு நிறம் ஆகியவற்றை தேர்ந்தெடுக்க வேண்டும். மகிழுந்தின் வியாபார முத்திரையைத் தேர்ந்தெடுக்க 2 வழிகளும் ஒவ்வொரு வியாபார முத்திரைக்கும் மகிழுந்தின் வகையை தேர்ந்தெடுக்க 3 வழிகளும் ஒவ்வொரு வகையிலும் நிறங்களை தேர்ந்தெடுக்க 5 வழிகளும் உள்ளன. எனவே, பெருக்கல் விதியின் படி, 2 × 3 × 5 = 30 வழிகளில் மகிழுந்துகளை தேர்ந்தெடுக்க முடியும்.

எடுத்துக்காட்டு 4.6 காஞ்சிபுரத்தில் உள்ள ஜவுளிக்கடையில் ஒரு பெண் ஒரு பட்டுப் புடைவையையும், ஒரு சுங்குடி புடவையையும் வாங்க நினைக்கிறார். கடையில் 20 வெவ்வேறு வகையான பட்டுப் புடவைகளும், 8 வெவ்வேறு வகையான சுங்குடி புடவைகளும் உள்ளன. புடவைகளை எத்தனை வகையில் அவரால் தேர்ந்தெடுக்க முடியும்?

தீர்வு:

ஒரு பெண் ஒரு பட்டு புடவையும் மற்றும் ஒரு சுங்குடி புடவையையும் தேர்ந்தெடுக்க வேண்டும். அந்த பெண் பட்டுப் புடவையைத் தேர்ந்தெடுக்க 20 வழிகளும் சுங்குடி புடவையை தேர்ந்தெடுக்க 8 வழிகளும் உள்ளன. இந்த இரண்டு புடவைகளையும் தேர்ந்தெடுக்க பெருக்கல் விதிப்படி, 20 × 8 = 160 வழிகள் உள்ளன.

எடுத்துக்காட்டு 4.7 ஒரு கிராமத்தில் உள்ளவர்களில் 80 சதவீதம் பேர் தென்னந்தோப்பையும், 65 சதவீதம் பேர் நெல் வயலையும் வைத்துள்ளனர். குறைந்தபட்சம் எத்தனை சதவீதம் பேர் இரண்டையும் வைத்திருப்பார்கள்? 

தீர்வு:

தென்னந்தோப்பை வைத்திருப்பவர்களின் சதவீதத்தை n(C) எனவும் நெல்வயலை வைத்திருப்பவர்களின் சதவீதத்தை n(P) எனவும் கொள்க. இங்கு n(C) = 80, n(P) = 65 என கொடுக்கப்பட்டு உள்ளது. சேர்த்தல் - நீக்கல் கொள்கையின் படி, n(C ∩ P) = n(C) + n(P) - n(C ∪ P) n(C ∪ P) -ன் பெரும மதிப்பு 100. எனவே, n(C ∩ P) - ன் குறைந்தபட்ச மதிப்பு 80 + 65 -100 = 45.

எனவே, குறைந்தபட்சம் 45 சதவீதம் பேர் இரண்டையும் வைத்திருப்பார்கள்.

குறிப்பு: அடுத்துவரும் கணக்குகளில் 'எழுத்துச்சரம்' என்ற கருத்தை பயன்படுத்த உள்ளோம். எழுத்துச்சரம் என்பது எழுத்துகளை ஒன்றன் பின் ஒன்றாக வரிசையாக அமைப்பது ஆகும். a, b, c மற்றும் d என்ற எழுத்துகளைக் கொண்டு உருவாக்கப்படும் மூன்று எழுத்துச் சரங்க ளை aaa, abb, bda, dca, cdd.... என எழுதலாம்.

எடுத்துக்காட்டு 4.8

(i) BIRD என்ற ஆங்கில வார்த்தையில் உள்ள 4 எழுத்துகளையும் பயன்படுத்தி எழுத்துகள் திரும்ப வராமல் எத்தனை எழுத்துச் சரங்களை உருவாக்கலாம். 

(ii) PRIME என்ற ஆங்கில வார்த்தையில் உள்ள 5 எழுத்துகளையும் பயன்படுத்தி எழுத்துகள் திரும்ப வராமல் எத்தனை எழுத்துச் சரங்களை உருவாக்கலாம்.

தீர்வு:

(i) 4 காலி இடங்களை 4 எழுத்துகளைக் கொண்டு எத்தனை வழிகளில் நிரப்பலாமோஅத்தனை 4 எழுத்துச் சரங்கள் இருக்கும். இதில் எழுத்துகள் திரும்பவரக்கூடாது என்பதை நினைவில் கொள்ள வேண்டும். முதல் இடத்தை B, I, R, D என்ற எழுத்துகளில் ஒன்றினைக் கொண்டு 4 வெவ்வேறான வழிகளில் நிரப்பலாம். இதே போல, இரண்டாவது இடத்தை மீதமுள்ள 3 எழுத்துகளைக் கொண்டு 3 வெவ்வேறான வழிகளிலும், மூன்றாவது இடத்தை 2 வழியிலும் நிரப்பலாம், நான்காவது இடத்தை 1 வழியிலும் நிரப்பலாம்.

ஆகவே, 4 இடங்களை நிரப்பும் வழிகளின் எண்ணிக்கை, பெருக்கல் விதிப் படி 4 × 3 × 2 × 1 = 24. எனவே, தேவையான எழுத்துச் சரங்களின் எண்ணிக்கை 24 ஆகும்.

(ii) இங்கு 5 இடங்களை நிரப்ப 5 வெவ்வேறான எழுத்துகள் உள்ளன. முதல் இடத்தை P,R,I,M,E என்ற எழுத்துகளில் ஏதேனும் ஒன்றைக் கொண்டு 5 வழிகளில் நிரப்பலாம். முதல் இடத்தை 5 எழுத்துகளில் ஏதேனும் ஒன்றைக் கொண்டு நிரப்பிய பின்பு, மீதமுள்ள 4 எழுத்துகளைக் கொண்டு இரண்டாவது இடத்தையும், மூன்றாம் இடத்தை நிரப்ப 3 எழுத்துக்களும் மேலும் நான்காம் இடத்தை நிரப்ப 2 எழுத்துகளும் உள்ளன. மீதமுள்ள கடைசி எழுத்தை ஐந்தாம் இடத்தில் நிரப்பலாம். எனவே,ஐந்து இடங்களை நிரப்பும் வகைகளின்எண்ணிக்கை 5 × 4 × 3 × 2 × 1 = 120.

குறிப்பு: இந்த இரு நிலைகளுக்கும் இடையே உள்ள ஒப்புமையை கவனிக்க.

எடுத்துக்காட்டு 4.9 FLOWER என்ற வார்த்தையில் உள்ள 6 எழுத்துகளைக் கொண்டு கீழ்க்காணும் கட்டுப்பாடுகளுடன் எத்தனை எழுத்துச் சரங்களை உருவாக்கலாம்.

(i) F இல் தொடங்க வேண்டும் அல்லது R இல் முடிக்க வேண்டும்.

(ii) F இல் தொடங்கவோ, R இல் முடிக்கவோ கூடாது. 

தீர்வு :

எந்த ஒரு எழுத்துச் சரத்திலும் F, L, O, W, E, R என்ற எழுத்துகள் ஒவ்வொன்றும் ஒரே ஒரு முறைதான் வரும். 

(i) ஒரு எழுத்துச் சரத்தை F இல் தொடங்கினால் மீதமுள்ள ஐந்து இடங்களை L, O, W, E, R என்ற எழுத்துகளைக் கொண்டு நிரப்பலாம். 

எழுத்துகளைத் திரும்ப பயன்படுத்த முடியாது என்பதால் 2 ஆவது, 3 ஆவது, 4 ஆவது, 5 ஆவது மற்றும் 6 ஆவது இடங்களை முறையே 5, 4, 3, 2 மற்றும் 1 வழிகளில் நிரப்பலாம். எனவே பெருக்கல் விதிப்படி, F இல் தொடங்கும் எழுத்துச் சரங்களை 5 × 4 × 3 × 2 × 1 = 120 வழிகளில் அமைக்கலாம்.

ஒரு சரம் R இல் முடியவேண்டும் எனில் மீதமுள்ள 5 இடங்களை F, L, O, W, E என்ற எழுத்துகளைக் கொண்டு நிரப்பலாம்.

மேற்சொன்னது போலவே R இல் முடியும் எழுத்துச் சரங்களையும் 120 வழிகளில் அமைக்கலாம்.

ஒர் சரம் F இல் தொடங்கி R இல் முடியும் எனில், மீதமுள்ள 4 இடங்களை L, O, W, E என்ற எழுத்துகளைக் கொண்டு நிரப்பலாம்.

மேற்கூறியது போலவே, F இல் தொடங்கி R இல் முடியும் 6 எழுத்துச் சரங்களின் எண்ணிக்கை 4 × 3 × 2 × 1 = 24.

சேர்த்தல் - நீக்கல் கொள்கையின் படி, F இல் தொடங்க வேண்டும் அல்லது R இல் முடிக்க வேண்டும் என்றவாறுள்ள எழுத்துச் சரங்களின் எண்ணிக்கை 120 + 120 – 24 = 216 ஆகும்.

(ii) F இல் தொடங்கவோ, R இல் முடிக்கவோ கூடாத எழுத்துச் சரங்களின் எண்ணிக்கைஆனது (i) இல் கணக்கிடப்படவில்லை. இது மட்டுமல்லாமல் F, L, O, W, E, R என்ற எழுத்துகளை திரும்ப வராதவாறு உள்ள எல்லா 6 எழுத்துச் சரங்களின் எண்ணிக்கையை கணக்கிடவேண்டும். 

இப்பொழுது, முதல் இடத்தை இந்த 6 எழுத்துகளில் ஏதேனும் ஒன்றை பயன்படுத்தியும், இரண்டாவது இடத்தை மீதமுள்ள 5 எழுத்துகளில் ஏதாவது ஒன்றை பயன்படுத்தியும், இதுபோலவே, மற்ற இடங்களையும் நிரப்பக் கிடைக்கும் எழுத்துச் சரங்களின் எண்ணிக்கை 6 × 5 × 4 × 3 × 2 × 1 = 720. F இல் தொடங்கவோ R இல் முடிக்கவோ கூடாத எழுத்துச் சரங்களின் எண்ணிக்கையை, மொத்த எழுத்துச் சரங்களின் எண்ணிக்கையில் இருந்து F இல் தொடங்கி அல்லது R இல் முடிக்கும் எழுத்துச் சரங்களின் எண்ணிக்கையை கழிக்க பெறலாம். இதன் மதிப்பு 720 – 216 = 504 ஆகும்.

எடுத்துக்காட்டு 4.10 முதலில் இரண்டு வெவ்வேறான ஆங்கில எழுத்துகளையும் அதனைத்தொடர்ந்து நான்கு வெவ்வேறான எண்களையும் அல்லது முதலில் இரண்டு வெவ்வேறான எண்களையும் அதனைத்தொடர்ந்து நான்கு வெவ்வேறான எழுத்துகளையும் கொண்டு எத்தனை வெவ்வேறான உரிமத் தட்டுகளை (Licence Plates) உருவாக்கலாம்?

தீர்வு:

இத்தீர்வினை இரு நிலைகளில் காணலாம்.

நிலை 1: முதலில் இரண்டு வெவ்வேறான ஆங்கில எழுத்துகளையும் நான்கு வெவ்வேறான எண்களையும் கொண்டு உருவாக்கும் உரிமத் தட்டுகளின் எண்ணிக்கை 26 × 25 × 10 × 9 × 8 × 7 = 32,76,000. 

நிலை 2: முதலில் நான்கு வெவ்வேறான எழுத்துகளையும் பின்னர் இரண்டு வெவ்வேறான எண்களையும் கொண்டு உருவாக்கும் உரிமத் தட்டுகளின் எண்ணிக்கை 10 × 9 × 26 × 25 × 24 × 23 = 3, 22,92,000 ஆகும்.

நிலை 1 இல் அல்லது நிலை 2 இல் உள்ளவாறு உருவாகும் உரிமத்தட்டுகளின் எண்ணிக்கை, கூட்டல் விதியின் படி, (26 × 25 × 10 × 9 × 8 × 7) + (10 × 9 × 26 × 25 × 24 × 23) = 3, 55,68,000 

எடுத்துக்காட்டு 4.11 7000-த்தை விட அதிகமாகவும் 8000-த்தை விட குறைவாகவும் உள்ள எண்களில் இலக்கங்கள் திரும்ப வராதவாறு உள்ள 5 ஆல் வகுபடும் எண்களின் எண்ணிக்கையினை காண்க. 

தீர்வு: 

7000-த்தை விட அதிகமாகவும் 8000-த்தை விட குறைவாகவும் உள்ள எண்கள், 4-இலக்கங்களைக் கொண்டு இருக்க வேண்டும். எனவே, அதன் 1000 மாவது இடத்தில் 7 இருக்க வேண்டும். மேலும், இது 5 ஆல் வகுபட வேண்டியுள்ளதால் ஒன்றாவது இடம் 0 அல்லது 5 ஆக இருக்கவேண்டும்.

இலக்கங்கள் திரும்ப வராது என்பதால், 100 ஆவது மற்றும்  10 ஆவது இடங்களை மீதமுள்ள எண்களைக் கொண்டு முறையே 8 மற்றும் 7 வழிகளில் நிரப்பலாம்.

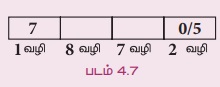
எனவே, தேவையான எண்களின் எண்ணிக்கை 1 × 8 × 7 × 2 = 112.

எடுத்துக்காட்டு 4.12 இலக்கங்கள் திரும்ப வராமல் எத்தனை 4-இலக்க இரட்டைப் படை எண்களை 0, 1, 2, 3 மற்றும் 4 ஆகிய எண்களை கொண்டு அமைக்கலாம்? 

தீர்வு:

இதில் இரண்டு கட்டுப்பாடுகள் உள்ளன.

1. 4-இலக்க எண் எனவே 1000 மாவது இடத்தில் 0 வரக்கூடாது. 

2. இரட்டைப்படை எண் என்பதால் ஒன்றாம் இடத்தில் 0, 2 அல்லது 4 வர வேண்டும்.

ஒன்றாம் இடத்தில் 0 உள்ளவாறு அல்லது 0 இல்லாதவாறு எனக்கொண்டு இக்கணக்கினை இரண்டு நிலைகளில் தீர்வு காணலாம்.

நிலை 1:  ஒன்றாம் இடத்தில் 0 உள்ளபோது 1000மாவது இடத்தை பூர்த்தி செய்ய 4 வழிகளும், 100ஆவது இடத்தை பூர்த்தி செய்ய 3 வழிகளும், 10ஆவது இடத்தை பூர்த்தி செய்ய 2 வழிகளும் உள்ளன. எனவே, ஒன்றாம் இடத்தில் 0 உள்ளவாறு 4 × 3 × 2 × 1 = 24 எண்களை உருவாக்கலாம்.

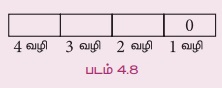
நிலை 2 : ஒன்றாம் இடத்தில் 0 இல்லாதபோது 2 அல்லது 4 என்ற இரு எண்களைக் கொண்டு ஒன்றாம் இடத்தை 2 வழிகளில் பூர்த்தி செய்யலாம், 1000ஆவது இடத்தை பூர்த்தி செய்ய 3 வழிகளும், 100ஆவது இடத்தை பூர்த்தி செய்ய 3 வழிகளும் மற்றும் 10ஆவது இடத்தை பூர்த்தி செய்ய 2 வழிகளும் உள்ளன.

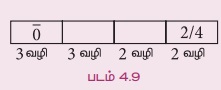
எனவே, ஒன்றாம் இடத்தில் 0 இல்லாதவாறு 3 × 3 × 2 × 2 = 36 எண்களை உருவாக்கலாம்.

4-இலக்க இரட்டைப்படை எண்களின் எண்ணிக்கை கூட்டல் விதியின் படி 24 + 36 = 60.

எடுத்துக்காட்டு 4.13 5 நாணயங்களை ஒரு முறை சுண்டும் போது ஏற்படும் விளைவுகளின் மொத்த எண்ணிக்கையைக் காண்க. 

தீர்வு:

ஒரு நாணயத்தைச் சுண்டும் போது {தலை, பூ} என 2 விளைவுகள் கிடைக்கும். எண்ணுதல் விதிப்படி, 5 நாணயங்களைச் சுண்டும் போது ஏற்படும் விளைவுகளின் எண்ணிக்கை 2 × 2 × 2 × 2 × 2 = 25 = 32.

குறிப்பு: பொதுவாக, n நாணயங்களை சுண்டும் போது ஏற்படும் விளைவுகளின் எண்ணிக்கை 2n ஆகும்.

எடுத்துக்காட்டு 4.14

(i) 5 பந்துகளை எத்தனை வழிகளில் 3 பெட்டிகளில் விநியோகிக்கலாம். 

(ii) 3 பந்துகளை எத்தனை வழிகளில் 5 பெட்டிகளில் விநியோகிக்கலாம்.

தீர்வு:

(i) ஒவ்வொரு பந்தையும் 3 வெவ்வேறான பெட்டிகளில் 3 வழிகளில் வைக்கலாம். எனவே, பெருக்கல் விதிப்படி 5 பந்துகளை 3 பெட்டிகளில் 3 × 3 × 3 × 3 × 3 = 36 = 243 வழிகளில் விநியோகிக்கலாம். 

(ii) ஒவ்வொரு பந்தையும் 5 வெவ்வேறான பெட்டிகளில் 5 வழிகளில் வைக்கலாம். எனவே, பெருக்கல் விதிப்படி 3 பந்துகளை 5 பெட்டிகளில் 5 × 5 × 5 = 53 = 125 வழிகளில் விநியோகிக்கலாம்.

குறிப்பு: இது போன்ற கணக்குகளில் ஏற்படும் குழப்பங்களைத் தவிர்க்க பொருட்களை (பந்துகளை) எடுத்து, இடங்களில் (பெட்டிகளில்) விநியோகிக்க வேண்டும் என்பதை நினைவில் கொள்ள வேண்டும்.

பொதுவாக, n வெவ்வேறான பொருட்களை m இடங்களில் வைக்க மொத்தம் mn வழிகள் உள்ளன.

எடுத்துக்காட்டு 4.15 ஒரு அறையில் 10 விளக்குகள் உள்ளன. ஒவ்வொன்றையும் தனித்தனியாக இயக்க முடியும். அந்த அறையை எத்தனை வழிகளில் ஒளியூட்டலாம்.

தீர்வு:

ஒவ்வொரு விளக்குகளையும் தனித்தனியாக ஒளியூட்டுதல் அல்லது அணைத்தல் என இரண்டு வழிகள் உள்ளன. எனவே அத்தனை விளக்குகளையும் 210 வழிகளில் இயக்கலாம். இதில், எல்லா விளக்குகளையும் அணைத்து வைக்கும் வகையும் உள்ளடங்கியுள்ளது. இங்கு எல்லா விளக்குகளையும் அணைத்து வைத்து அறையை ஒளியூட்ட முடியாது. ஆதலால், அந்த அறையை ஒளியூட்ட 210 - 1 = 1024 - 1 = 1023 வழிகள் உள்ளன.

எண்ணுவதற்கு பயன்படும் மற்றொரு முக்கிய கருவியை கீழ்க்காணுமாறு எடுத்துரைக்கலாம்.

புறாக் கூடு கொள்கை (Pigeonhole Principle)

ஒரு புறாக் கூட்டுத் தொகுப்பை நோக்கி ஒரு புறாக் கூட்டம் பறந்து வருவதாகக் கொள்வோம். புறா கூடுகளின் எண்ணிக்கையை விட புறாக்களின் எண்ணிக்கை அதிகமாக இருந்தால், குறைந்த பட்சம் ஒரு புறா கூட்டிலாவது குறைந்த பட்சம் இரண்டு புறாக்கள் இருக்க வேண்டும் என்பதாகும். இதனை பொதுமைப்படுத்தி பல்வேறு வகையான பொருட்களுக்கும் பயன்படுத்தலாம். அதாவது, k பெட்டிகளில் k + 1 பொருட்கள் இருந்தால், குறைந்தபட்சம் ஒரு பெட்டியிலாவது இரண்டு அல்லது அதற்கு மேற்பட்ட பொருட்கள் இருக்க வேண்டும் என்பதாகும்.

சில உதாரணங்கள்:

1. எந்த ஒரு 27 ஆங்கில வார்த்தைகளைக் கொண்ட தொகுப்பிலும் குறைந்த பட்சம் இரண்டு வார்த்தைகளாவது ஒரே எழுத்தில் தொடங்க வேண்டும். (ஆங்கிலத்தில் 26 எழுத்துகள் மட்டுமே உள்ளது.)

2. ஒரு வாரத்தில் உள்ள 5 வேலை நாட்களில் நடைபெறும் எந்த 6 கூட்டங்களில் குறைந்த பட்சம் இரண்டு கூட்டங்களாவது ஒரே நாளில் நடை பெற வேண்டும்.

வரிசை மாற்றங்கள் மற்றும் சேர்வுகளை புரிந்து கொள்ள நாம் “காரணியப் பெருக்கம்” என்ற கருத்தாக்கத்தை அடுத்த பகுதியில் காண்போம்.