இருபடிச் சமன்பாட்டின் மூலங்களின் தன்மை

இருபடிச் சமன்பாட்டின் மூலங்களின் தன்மை (Nature of Roots of a Quadratic Equation)

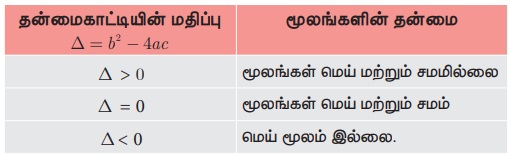
ax2 + bx +c = 0, a ≠ 0 எனும் இருபடிச் சமன்பாட்டின் மூலங்களை 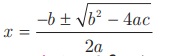எனும் சூத்திரத்தைப் பயன்படுத்திக் காணலாம். இருபடிச் சமன்பாட்டின் ‘தன்மைகாட்டி' (குறியீடு Δ] என அழைக்கப்படும். b2 - 4ac மூலங்களின் தன்மையைக் கீழ்க்கண்டவாறு தெரிவிக்கிறது.

எடுத்துக்காட்டு 3.40 

பின்வரும் இருபடிச் சமன்பாடுகளின் மூலங்களின் தன்மையைக் காண்க. 

(i) x2 − x − 20 = 0

(ii) 9x2 − 24x + 16 = 0

(iii) 2x2 − 2x + 9 = 0

தீர்வு 

(i) x2 − x − 20 = 0

இங்கு, a = 1, b = -1, c = -20 

தன்மைகாட்டி, Δ = b2 − 4ac

Δ = (− 1)2 − 4(1) (−20) = 81

Δ = 81 > 0

எனவே, சமன்பாட்டின் மூலங்கள் மெய் மற்றும் சமமில்லை.

(ii) 9x2 − 24x + 16 = 0

இங்கு, a = 9 , b = −24 , c = 16

தன்மைகாட்டி, Δ = b2 − 4ac = (−24)2 − 4 (9 )(16) = 0

∆ = 0 . 

எனவே, சமன்பாட்டின் மூலங்கள் மெய் மற்றும் சமம். 

(iii) 2x2 − 2x + 9 = 0

இங்கு, a = 2 , b = −2 , c = 9

தன்மைகாட்டி, Δ  = b2 − 4ac = (−2)2 − 4(2)(9) = −68

Δ = − 68 < 0 

எனவே, இருபடிச் சமன்பாட்டிற்கு மெய் மூலங்கள் இல்லை. 

எடுத்துக்காட்டு 3.41 

(i) இருபடிச் சமன்பாட்டு kx 2 − (8k + 4) + 81 = 0 -யின் மூலங்கள் மெய் மற்றும் சமம் எனில், 'k', - யின் மதிப்பைக் காண்க. 

(ii) (k + 9) x2 + (k + 1)x + 1 = 0 - யின் மூலங்கள் மெய் இல்லை எனில், k-யின் மதிப்பைக் காண்க. 

தீர்வு 

(i) kx 2 − (8k + 4)x + 81 = 0 

சமன்பாட்டின் மூலங்கள் மெய் மற்றும் சமம். எனவே, Δ = 0. அதாவது, b2 − 4ac = 0

இங்கு, a = k , b = −(8k + 4), c = 81

எனவே, [ −(8k + 4)]2 − 4(k )(81) = 0 

64k2 + 64k + 16 − 324k = 0

64k2 − 260k + 16 = 0

4ஆல் வகுக்க, 16k2 − 65k + 4 = 0

(16k − 1) (k − 4) = 0 ⇒ k = 1/16 அல்லது k = 4

(ii) (k + 9) x2 + (k + 1)x + 1 = 0

சமன்பாட்டின் மூலங்கள் மெய் இல்லை. எனவே, Δ < 0

அதாவது, b2 − 4ac < 0

இங்கு, a = k + 9, b = k + 1 , c = 1

எனவே, (k + 1)2 − 4(k + 9) (1) < 0

k 2 + 2k + 1 – 4k − 36 < 0

k2 − 2k − 35 < 0

(k + 5) (k − 7) < 0

எனவே, − 5 < k < 7 .     {α < β (x − α) (x − β) < 0 எனில், α < x < β }.

எடுத்துக்காட்டு 3.42 

x2 (p2 + q 2) + 2x(pr + qs) + r2 + s2 = 0 எனும் சமன்பாட்டிற்கு மெய் மூலங்கள் இல்லை எனக் காட்டுக. மேலும் ps = qr, எனில், மூலங்கள் மெய்யானவை மற்றும் சமம் என நிறுவுக.

தீர்வு 

கொடுக்கப்பட்ட இருபடிச் சமன்பாடு, x2 (p2 + q2 ) + 2x ( pr + qs) + r2  + s2  = 0

இங்கு, a = p2 +q2 , b = 2(pr +qs), c = r2 + s2

தன்மைகாட்டி,  Δ = b2 − 4ac  =  [2( pr + qs)]2 − 4( p2  + q2 )( r 2 + s2 )

= 4 [p2r2 + 2pqrs + q2s2 − q2r2 – p2s2 – q2r2 – q2s2]

= 4 [–p2s2 + 2pqrs − q2r2] = −4 [(ps − qr)2] <0           ...(1)

Δ = b2 − 4ac < 0, எனவே, மூலங்கள் மெய் இல்லை.

மேலும், ps = qr எனில், Δ = − 4[ps – qr]2 = - 4[qr − qr]2 = 0 ( (1)-ஐப் பயன்படுத்தி)

ஆகவே, Δ = 0 if ps = qr எனில், மூலங்கள் மெய்யாகவும், சமமாகவும் இருக்கும்.