அணியின் வரிசை

அணியின் வரிசை (Order of a Matrix)

A என்ற ஓர் அணியில் m நிரைகளும், n நிரல்களும் இருப்பின் அணி A -ன் வரிசை (நிரைகளின் எண்ணிக்கை) × (நிரல்களின் எண்ணிக்கை) ஆகும். இதனை m × n என எழுதலாம். இங்கு m × n என்பது m, n ஆகியவற்றின் பெருக்கற்பலன் அல்ல.

பொதுவாக m நிரல்களும் n நிரல்களும் (வரிசை m × n) உடைய A என்ற அணியைப் பின்வருமாறு எழுதலாம்.

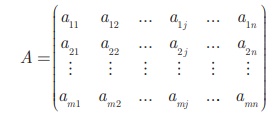
இங்கு, a11, a12,...  என்பன அணியின் உறுப்புகள் ஆகும். a11 என்பது அணியின் முதலாவது நிரை மற்றும் முதலாவது நிரல் இடத்திலுள்ள உறுப்பாகும். a12 என்பது அணியின் முதலாவது நிரை மற்றும் இரண்டாவது நிரல் இடத்திலுள்ள உறுப்பாகும். இவற்றைப் போலவே மற்ற உறுப்புகளை எழுதலாம்.

பொதுவாக, aij என்பது i ஆவது நிரை மற்றும் j ஆவது நிரல் இடத்திலுள்ள உறுப்பாகும். 

இதனைக் கொண்டு A அணியை A = (aij )m × n  என்று எழுதலாம். இங்கு i = 1,2,....m மற்றும் j = 1,2,.....n.

A = (aij)m ×n  is mn என்ற அணியின் மொத்த உறுப்புகள் mn ஆகும்.

முன்னேற்றச் சோதனை

1. 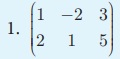என்ற அணியின் இரண்டாவது நிரை மற்றும் மூன்றாவது நிரலில் உள்ள உறுப்பு எது? 

2. 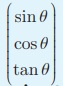என்ற அணியின் வரிசை என்ன? 

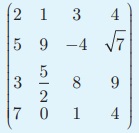
3. கீழுள்ள அணியில் a11, a22, a33, a44 என்பவை குறிக்கும் மதிப்புகளை எழுதுக. 

குறிப்பு

அணியின் வரிசையைக் குறிப்பிடும்போது, முதலில் நிரைகளின் எண்ணிக்கையும் அதனைத் தொடர்ந்து நிரல்களின் எண்ணிக்கையும் இருக்கும். 

எடுத்துக்காட்டாக,

செயல்பாடு 4 

(i) ஒரு நாள்காட்டியில் எதாவது ஒரு குறிப்பிட்ட வருடத்தில் ஒரு குறிப்பிட்ட மாதத்தை எடுத்துக் கொள்ளவும். 

(ii) நாள்காட்டி அட்டையில் நாள்களைக் கொண்டு அணிகளை அமைக்கவும். 

(iii) கீழ்க்கண்ட வரிசையுடைய அனைத்து அணிகளையும் அமைக்கவும். 2 × 2, 3 × 2, 2 × 3, 3 × 3, 4 × 3. 

(iv) கொடுக்கப்பட்ட நாள்காட்டி அட்டையிலிருந்து மிகப் பெரிய வரிசையுடைய அணியைக் கண்டுபிடி. 

(v) நடைமுறை வாழ்வில் உள்ள தகவல்களைக் கையாள்வதில் அணிகள் எவ்வாறு பயன்படுகிறது என்பதைக் குறிப்பிடுக.