அணிகளின் வகைகள்

அணிகளின் வகைகள் (Types of Matrices)

இப்பகுதியில், அணிகளின் வகைகள் சிலவற்றை வரையறை செய்வோம். 

1. நிரை அணி (Row Matrix)

ஓர் அணியில் ஒரே ஒரு நிரையும், பல நிரல்களும் இருந்தால் அவ்வணி நிரை அணி எனப்படும். நிரை அணியை நிரை வெக்டர் (row vector) எனவும் கூறலாம்.

எடுத்துக்காட்டாக, A = (8 9 4 3), B = (-√3/2 1 √3)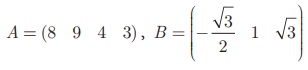 

என்பன முறையே 1 × 4 மற்றும் 1 × 3 வரிசையுடைய நிரை அணிகள் ஆகும்.

பொதுவாக, A = (a11 a12 a13  … a1n) என்பது 1 × n வரிசையில் உள்ள நிரை அணி ஆகும். 

2. நிரல் அணி (Column Matrix)

ஓர் அணியில் ஒரே ஒரு நிரலும், பல நிரைகளும் இருந்தால் அவ்வணி 'நிரல் அணி' எனப்படும் இதனை நிரல் வெக்டர் (column vector) எனவும் கூறலாம்.

எடுத்துக்காட்டாக, 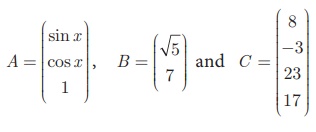என்பன 3 × 1, 2 × 1 மற்றும் 4 × 1 வரிசையுடைய நிரல் அணிகள் ஆகும்.

பொதுவாக, என்பது m × 1 வரிசையுடைய நிரல் அணி ஆகும்.

3. சதுர அணி (Square Matrix)

ஓர் அணியின் நிரைகளின் எண்ணிக்கையானது நிரல்களின் எண்ணிக்கைக்குச் சமமாக இருப்பின் அவ்வணி சதுர அணி எனப்படும். m = n எனில், A = (aij )m ×n என்பது சதுர அணியைக் குறிக்கும்.

எடுத்துக்காட்டாக, 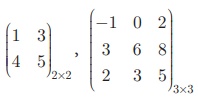என்பன சதுர அணிகள் ஆகும்.

பொதுவாக 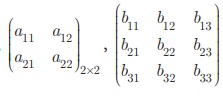என்பன 2 × 2 மற்றும் 3 × 3 வரிசையுடைய சதுர அணிகள் ஆகும். A = (aij )m ×m என்பது m வரிசையுடைய ஒரு சதுர அணி ஆகும்.

வரையறை: ஒரு சதுர அணியில், a11, a22, a33, . . .  என்பன சதுர அணியின் முதன்மை மூலைவிட்ட உறுப்புகள் எனப்படும். இவை aij (i=j), என்ற அமைப்பில் இருக்கும் உறுப்புகளாகும். எடுத்துக்காட்டாக, 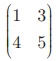 என்ற அணியில் 1 மற்றும் 5 என்பன முதன்மை மூலைவிட்ட உறுப்புகளாகும்.

4. மூலைவிட்ட அணி (Diagonal Matrix)

ஒரு சதுர அணியில் முதன்மை மூலை விட்டத்திற்கு மேலேயும் கீழேயும் உள்ள அனைத்து உறுப்புகளும் பூச்சியங்கள் எனில் அந்த அணி மூலைவிட்ட அணி எனப்படும்.

அதாவது, ஒரு சதுர அணி A = (aij) மூலைவிட்ட அணி எனில், aij  = 0 i ≠ j என இருக்கவேண்டும். சில மூலைவிட்ட உறுப்புகள் பூச்சியங்களாக இருக்கலாம், ஆனால் அனைத்தும் பூச்சியமாக இருக்கக்கூடாது.

எடுத்துக்காட்டாக, 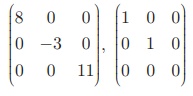என்பன மூலைவிட்ட அணிகள் ஆகும்.

5. திசையிலி அணி (Scalar Matrix)

ஒரு மூலைவிட்ட அணியில் முதன்மை மூலைவிட்ட உறுப்புகள் அனைத்தும் சமமாக இருப்பின் அந்த அணி திசையிலி அணி எனப்படும்.

எடுத்துக்காட்டாக, 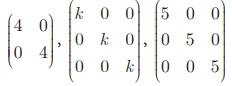என்பன திசையிலி அணிகள் ஆகும்.

பொதுவாக, A = (aij )m ×m  ஒரு திசையிலி அணி எனில்,

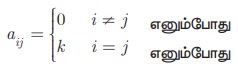
இங்கு k என்பது ஒரு மாறிலி ஆகும். 

6. சமனி (அல்லது) அலகு அணி Identity (or) Unit Matrix

ஒரு சதுர அணியில் முதன்மை மூலைவிட்ட உறுப்புகள் ஒவ்வொன்றும் 1 ஆகவும் மற்ற அனைத்து உறுப்புகளும் பூச்சியம் எனில், அந்த அணி சமனி அணி அல்லது அலகு அணி எனப்படும்.

பொதுவாக, சதுர அணி A = (aij) என்பது ஓர் அலகு அணி எனில், aij  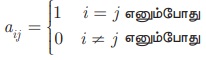= n வரிசையுடைய அலகு அணியை In. எனக் குறிக்கலாம்.

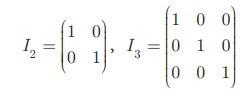என்பன முறையே 2 மற்றும் 3 வரிசையுடைய அலகு அணிகள் ஆகும். 

7. பூச்சிய அணி (அல்லது) வெற்று அணி (Zero matrix (or) Null matrix)

ஓர் அணியிலுள்ள அனைத்து உறுப்புகளும் பூச்சியம் எனில், அந்த அணி பூச்சிய அணி அல்லது வெற்று அணி எனப்படும்.

எடுத்துக்காட்டாக, 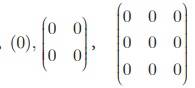என்பன முறையே 1 × 1, 2 × 2 மற்றும் 3 × 3 என வேறுபட்ட வரிசையுடைய பூச்சிய அணிகள் ஆகும். n × n வரிசையுடைய பூச்சிய அணியை On. எனக் குறிப்பிடலாம். 

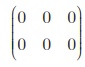என்பது 2 × 3 வரிசையுடைய பூச்சிய அணி ஆகும். 

8. நிரை நிரல் மாற்று அணி (Transpose of a matrix)

A என்ற அணியின் நிரைகளை நிரல்களாகவும் அல்லது நிரல்களை நிரைகளாகவும் மாற்றக் கிடைக்கும் அணி A -யின் நிரை நிரல் மாற்று அணி எனப்படும். A -யின் நிரை நிரல் மாற்று அணியை AT எனக் குறிப்பிடலாம்.

அணி A - யின் வரிசை m × n எனில், AT - யின் வரிசை n × m ஆகும்.

(AT)T = A. எனக் கிடைக்கும். 

9. முக்கோண அணி (Triangular Matrix)

ஒரு சதுர அணியில் முதன்மை மூலைவிட்டத்திற்கு மேலே உள்ள உறுப்புகள் அனைத்தும் பூச்சியம் எனில், அந்த அணி கீழ் முக்கோண அணி எனப்படும்.

ஒரு சதுர அணியில் முதன்மை மூலைவிட்டத்திற்குக் கீழே உள்ள உறுப்புகள் அனைத்தும் பூச்சியமாக இருந்தால் அந்த அணி மேல் முக்கோண அணி எனப்படும். 

வரையறை: 

ஒரு சதுர அணி A = (aij)n ×n -யில், i > j எனும்போது, aij = 0 எனில், அது மேல் முக்கோண அணி என்றும் i < j  எனும்போது aij  = 0 எனில், அது கீழ் முக்கோண அணி என்றும் அழைக்கப்படுகிறது.

எடுத்துக்காட்டாக, A = என்பது மேல் முக்கோண அணி மற்றும்

B = 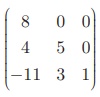என்பது கீழ் முக்கோண அணி ஆகும். 

சம அணிகள் (Equal Matrices)

அணிகள் A மற்றும் B ஆகியவற்றின் வரிசைகள் மற்றும் A -யில் உள்ள ஒவ்வோர் உறுப்பும் B -யில் உள்ள ஒத்த உறுப்புகளுக்குச் சமம் எனில், A மற்றும் B ஆகியவை சம அணிகள் எனப்படும். அதாவது, அனைத்தும், i, j-களுக்கு aij = bij .

எடுத்துக்காட்டாக,

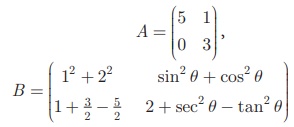எனில், A மற்றும் B ஒரே வரிசை கொண்டும் அனைத்து, i, j -களுக்கு aij = bij ஆகவும் உள்ளது.

ஆகவே A மற்றும் B என்பன சம அணிகள் ஆகும்.

முன்னேற்றச் சோதனை

1. ஒரு நிரல் அணியில் உள்ள நிரல்களின் எண்ணிக்கை _______. 

2. ஒரு நிரை அணியில் உள்ள நிரைகளின் எண்ணிக்கை _______. 

3. எந்தவோர் அலகு அணியிலும் மூலைவிட்டத்திலில்லாத உறுப்புகள் _______ ஆகும். 

4. 32 உறுப்புகளைக் கொண்ட சதுர அணி இருக்க முடியுமா?

எதிர் அணி (The negative of a matrix)

அணி -Am ×n -யின் எதிர் அணி Am ×n என்றவாறு அமையும். - A என்ற அணியில் உள்ள அனைத்து உறுப்புகளும் A - வில் உள்ள ஒத்த உறுப்புகளின் கூட்டல் நேர்மாறல்களாக இருக்கும்.

k என்ற எண்ணின் கூட்டல் நேர்மாறல் – k ஆகும். அதாவது - A -யின் ஒவ்வோர் உறுப்பும் A -யின் ஒத்த உறுப்புகளின் கூட்டல் நேர்மாறாக இருக்கும்.

எடுத்துக்காட்டாக, A =

எடுத்துக்காட்டு 3.56 

I, II, III என்ற மூன்று தொழிற்சாலைகளில் பணி புரியும் ஆண்கள், பெண்கள் பற்றிய விவரம் கீழ்க்கண்டவாறு கொடுக்கப்பட்டுள்ளது.

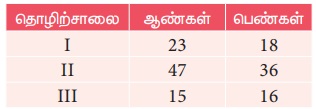
மேற்கண்ட தகவலை ஓர் அணி அமைப்பில் எழுதுக. இதில் இரண்டாவது நிரை மற்றும் முதலாவது நிரல் இடத்திலுள்ள உறுப்பு எதனைக் குறிக்கிறது? 

தீர்வு 

கொடுக்கப்பட்ட தகவல்களைக் கொண்டு 3 × 2 என்ற வரிசை கொண்ட அணியை பின்வருமாறு எழுதலாம்.

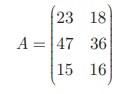
இரண்டாவது நிரை மற்றும் முதல் நிரல் இடத்தில் உள்ள உறுப்பானது II-வது தொழிற்சாலையில் 47 ஆண்கள் பணிபுரியும் விவரத்தைக் குறிக்கிறது. 

எடுத்துக்காட்டு 3.57 

ஓர் அணியானது 16 உறுப்புகளைக் கொண்டிருந்தால், அந்த அணிக்கு எத்தனை விதமான வரிசைகள் இருக்கும்? 

தீர்வு 

ஓர் அணியின் வரிசை m × n எனில், அதற்கு mn உறுப்புகள் இருக்கும் என்பது நமக்குத் தெரியும். 16 உறுப்புகளைக் கொண்ட அணிக்கு இருக்கக்கூடிய அனைத்து வரிசைகளையும் காண்போம்.

நிரை, நிரலைப் பெருக்கினால் 16 கிடைக்கக்கூடிய இயல் எண்களின் சோடிகளைக் காண வேண்டும். அந்த விதமான வரிசைச் சோடிகள் (1,16), (16,1), (4,4), (8,2), (2,8)

எனவே, நமக்குக் கிடைக்கும் அணியின் வரிசைகள் 1 × 16, 16 × 1, 4 × 4, 2 × 8, 8 × 2

செயல்பாடு 5 

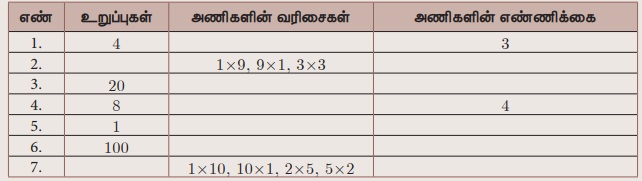
இரண்டாவது நிரலில் உள்ள உறுப்புகளின் எண்ணிக்கைக்கும் நான்காவது நிரலில் உள்ள அணிகளின் எண்ணிக்கைக்கும் உள்ள தொடர்பைக் காணமுடிகிறதா? ஆம் எனில், விடுபட்ட கட்டங்களை நிரப்புக.

எடுத்துக்காட்டு 3.58 

a ij = i2 j2 என்ற அமைப்பைக் கொண்ட 3 × 3 வரிசையுடைய அணியைக் காண்க.

தீர்வு 

3 × 3 வரிசையுடைய அணியின் பொது வடிவம் 

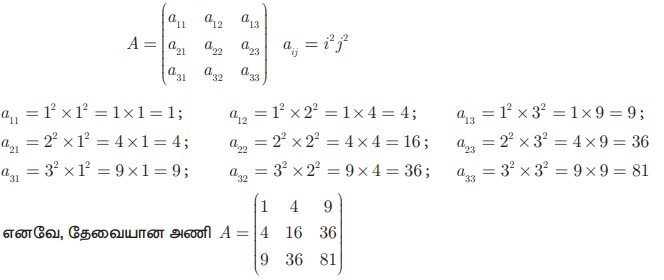
எடுத்துக்காட்டு 3.59 

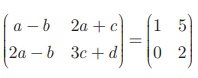என்ற அணி சமன்பாட்டிலிருந்து a, b, c, d மதிப்புகளைக் காண்க.

தீர்வு 

கொடுக்கப்பட்ட அணிகள் சமம். எனவே ஒத்த உறுப்புகள் சமம்.

ஆகையால்,

a − b = 1…(1)

2a + c = 5…(2)

2a − b = 0…(3)

3c + d = 2…(4)

(3) லிருந்து நாம் பெறுவது 

2a − b = 0

2a = b …(5)

2a = b என்பதை (1) -யில் பிரதியிட, a − 2a = 1 ⇒ a = −1

a = −1 என்பதை (5) -யில் பிரதியிட, 2(− 1) = b ⇒ b = −2

a = −1 என்பதை (2) -யில் பிரதியிட, 2(− 1) +c = 5   ⇒ c = 7

c = 7 என்பதை (4) –யில் பிரதியிட, 3(7) + d = 2 ⇒ d = −19

எனவே, a = −1, b = −2, c = 7, d = −19