நினைவு கூர்வதற்கான கருத்துகள்

நினைவு கூர்வதற்கான கருத்துகள்

· மூன்று மாறிகளில் அமைந்த நேரிய சமன்பாட்டு தொகுப்பிற்குப் பின்வருமாறு தீர்வுகள் அமையலாம். 

(i) ஒரே ஒரு தீர்வு 

(ii) எண்ணற்ற தீர்வு 

(iii) தீர்வு இல்லை 

· கோவையின் படி இரண்டாக இருப்பின் அக்கோவையை இருபடி கோவை என அழைக்கிறோம். ஓர் இருபடி கோவைக்கு அதிகபட்சமாக இரண்டு பூச்சியங்கள் உண்டு. மேலும் இந்தப் பூச்சியங்கள் X அச்சைச் சந்திக்கும்.

• ax2 + bx +c = 0, (a ≠ 0) என்ற இருபடிச் சமன்பாட்டின் மூலங்கள்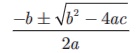

• ax2 + bx +c = 0, a ≠ 0 என்ற இருபடிச் சமன்பாட்டின்.

· α, β -வை மூலங்களாக உடைய இருபடிச் சமன்பாடு x2 − (α + β) x + αβ = 0. 

· ஓர் இருபடிச் சமன்பாட்டின் மூலங்களை பற்றி தன்மை காட்டி மூலம் (Δ = b 2 − 4ac) பின்வருமாறு அறியலாம். 

(i) Δ > 0 எனில், மூலங்கள் மெய், சமமல்ல. 

(ii) Δ = 0 எனில், மூலங்கள் மெய் மற்றும் சமம். 

(iii) Δ < 0 எனில், மூலங்கள் மெய் எண்கள் அல்ல. 

· இருபடிச் சமன்பாட்டை வரைப்படம் மூலம் தீர்த்தல். 

· செவ்வக வடிவில் நிரை மற்றும் நிரல்களால் உறுப்புகளை வரிசைப்படுத்தும் அமைப்பு அணி எனப்படும்.

· 'A' என்ற அணியில் m நிரைகளும் n நிரல்களும் இருப்பின் 'A' -யின் வரிசை (நிரைகளின் எண்ணிக்கை) × (நிரல்களின் எண்ணிக்கை) ஆகும். இதனை m × n என எழுதலாம். m × n என்பது m மற்றும் n-யின் பெருக்கற்பலன் அல்ல என்பது குறிப்பிடத்தக்கது. 

· அணிகளின் வகைகள் 

(i) ஓர் அணியில் ஒரே ஒரு நிரையும், பல நிரல்களும் இருந்தால் அவ்வணி நிரை அணி எனப்படும். நிரை அணியை நிரை வெக்டர் (row vector) எனவும் கூறலாம். 

(ii) ஓர் அணியில் ஒரே ஒரு நிரலும், பல நிரைகளும் இருந்தால், அவ்வணி நிரல் அணி எனப்படும். நிரல் அணியை நிரல் வெக்டர் எனவும் கூறலாம். 

(iii) ஓர் அணியின் நிரைகளின் எண்ணிக்கையானது நிரல்களின் எண்ணிக்கைக்குச் சமமாக இருப்பின் அவ்வணி சதுர அணி எனப்படும். 

(iv) ஓர் அணியிலுள்ள அனைத்து உறுப்புகளும் பூச்சியம் எனில், அந்த அணி பூச்சிய அணி அல்லது வெற்று அணி எனப்படும். 

(v) A என்ற அணியின் நிரைகளை நிரல்களாகவும் அல்லது நிரல்களை நிரைகளாகவும் மாற்றக் கிடைக்கும் அணி A-யின் நிரை நிரல் மாற்று அணி எனப்படும். இதனை AT எனக் குறிக்கலாம். 

(vi) ஒரு சதுர அணியில் முதன்மை மூலை விட்டத்திற்கு மேலேயும் கீழேயும் உள்ள அனைத்து உறுப்புகளும் பூச்சியங்கள் எனில் அந்த அணி மூலைவிட்ட அணி எனப்படும். 

(vii) ஒரு மூலைவிட்ட அணியில் முதன்மை மூலைவிட்ட உறுப்புகள் அனைத்தும் சமமாக இருப்பின் அந்த அணி திசையிலி அணி எனப்படும். 

(viii) ஒரு சதுர அணியில் முதன்மை மூலைவிட்ட உறுப்புகள் ஒவ்வொன்றும் 1 ஆகவும் மற்ற அனைத்து உறுப்புகளும் பூச்சியம் எனில், அந்த அணி சமனி அணி அல்லது அலகு அணி எனப்படும். 

(ix) ஒரு சதுர அணியில் முதன்மை மூலைவிட்டத்திற்கு மேலே உள்ள உறுப்புகள் அனைத்தும் பூச்சியம் எனில், அந்த அணி கீழ்முக்கோண அணி எனப்படும். ஒரு சதுர அணியில் முதன்மை மூலைவிட்டத்திற்குக் கீழே உள்ள உறுப்புகள் அனைத்தும் பூச்சியமாக இருந்தால் அந்த அணி மேல் முக்கோண அணி எனப்படும். 

(x) அணிகள் A மற்றும் B ஆகியவற்றின் வரிசைகள் மற்றும் A-யில் உள்ள ஒவ்வோர் உறுப்பும் B-யில் உள்ள ஒத்த உறுப்புகளுக்குச் சமம் எனில், A மற்றும் B ஆகியவை சம அணிகள் எனப்படும். அதாவது, aij = bij ∀ i, j.

· அணி Am×n -யின் எதிர் அணி - Am×n என்றவாறு அமையும். - A என்ற அணியில் உள்ள அனைத்து உறுப்புகளும் A -வில் உள்ள ஒத்த உறுப்புகளின் கூட்டல் நேர்மாறல்களாக இருக்கும்.

· அணிகளின் கூடுதல் மற்றும் கழித்தல் 

ஒரே வரிசையுடைய இரு அணிகளைக் கூட்டவோ அல்லது கழிக்கவோ முடியும். இரு அணிகளைக் கூட்டுவதற்கோ அல்லது கழிப்பதற்கோ அந்த அணிகளில் இருக்கின்ற ஒத்த உறுப்புகளைக் கூட்டவோ அல்லது கழிக்கவோ செய்ய வேண்டும்.

· அணியைத் திசையிலியால் பெருக்குதல் 

கொடுக்கப்பட்ட A என்ற அணியின் உறுப்புகளைப் பூச்சியமற்ற k என்ற எண்ணால் பெருக்கும்போது கிடைக்கும் புதிய அணி kA ஆகும். இதன் உறுப்புகள் அனைத்தும் k ஆல் பெருக்கப்பட்டிருக்கும். kA = (kaij) m×n என்பது A-யின் திசையிலி அணி பெருக்கல் எனப்படும். A = (aij) m×n எனில், kA அனைத்து i = 1, 2, ..., m ; j = 1, 2, ..., n ஆகும்.