அணிகளின் பெருக்கல் பண்புகள்

அணிகளின் பெருக்கல் (Multiplication of Matrices)

இரு அணிகளைப் பெருக்குவதற்கு, முதல் அணியின் நிரல்களின் எண்ணிக்கையானது இரண்டாவது அணியின் நிரைகளின் எண்ணிக்கைக்குச் சமமாக இருக்கவேண்டும்.

3 × 3 மற்றும் 3 × 2 என்ற அணிகளின் பெருக்கற்பலனை எடுத்துக்கொள்க.

அணியின் பெருக்கல் என்பது முதல் அணியின் நிரையில் உள்ள உறுப்புகளைக் கொண்டு இரண்டாவது அணியின் நிரல்களைப் பெருக்கிப் பின் கூட்டவேண்டும்.

எடுத்துக்காட்டாக, அணியின் பெருக்கல்

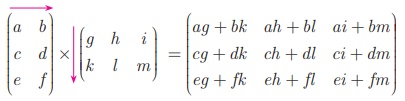
A என்ற அணியின் நிரல்களின் எண்ணிக்கையும் B - என்ற அணியின் நிரைகளின் எண்ணிக்கையும் சமமாக இருந்தால் மட்டுமே அதன் பெருக்கல் அணி AB -ஐக் காண முடியும்.

A என்ற அணியின் வரிசை m × n மற்றும் B என்ற அணியின் வரிசை n × p எனில், AB என்ற அணியின் வரிசை m × p ஆகும்.

அணி பெருக்கலின் பண்புகள் (Properties of Multiplication of Matrix)

(a) பொதுவாக அணியின் பெருக்கல் பரிமாற்று பண்பு உடையது அல்ல. 

அணி A-யின் வரிசை m × n மற்றும் B-யின் வரிசை n × p எனில், அணியின் பெருக்கல் AB என வரையறுக்கப்படுகிறது. ஆனால் அணியின் பெருக்கல் BA-ஐ வரையறுக்க முடியாது. அதேபோல், AB மற்றும் BA என்ற அணிகள் வரையறுக்கப்பட்டாலும்கூட, AB -யும் BA -யும் சமமாக இருக்க வேண்டிய அவசியமில்லை. பொதுவாக, AB ≠ BA.

(b) அணியின் கூட்டலைப் பொறுத்து அணி பெருக்கலானது பங்கீட்டு பண்பு உடையது. 

(i) A, B, C என்ற அணிகளின் வரிசைகள் m × n, n × p மற்றும் n × p எனில்,

A (B + C) = AB + AC (வலது பங்கீட்டு விதி) 

(ii) A, B, C என்ற அணிகளின் வரிசைகள் m × n, m × n மற்றும் n × p எனில், (A + B) C = AC + BC (இடது பங்கீட்டு விதி) 

(c) அணியின் பெருக்கல் சேர்ப்பு பண்பு உடையது

A, B, C என்ற அணிகளின் வரிசைகள் m × n, n × p மற்றும் p × q எனில்,

(AB)C = A(BC) ஆகும். 

(d) அணிகளின் பெருக்கலுக்கான அலகு அணி

A என்ற சதுர அணியின் வரிசை n × n மற்றும் அதே வரிசையுடைய அலகு அணி I எனில், AI = IA = A.

குறிப்பு 

• x மற்றும் y என்பன xy = 0 என்றவாறு இருக்கும் இரு மெய்யெண்கள் என்க. இவற்றில் x = 0 அல்லது y = 0 என இருக்கவேண்டும். ஆனால் இரண்டு அணிகளுக்கு இது உண்மையாக இருக்காது. 

• AB = 0 எனில், A = 0 அல்லது B = 0 அல்லது A, B = 0 ஆக இருக்க வேண்டியதில்லை. குறிப்பாக, இரண்டு பூச்சியமற்ற அணிகளின் பெருக்கல் பூச்சிய அணியைக் கொடுக்கலாம்.

விளக்கம் 

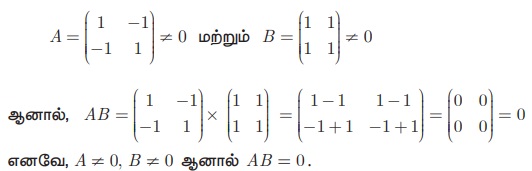
எடுத்துக்காட்டு 3.67 

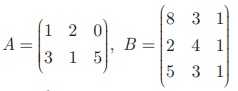எனில், A B-ஐக் காண்க. 

தீர்வு 

A என்ற அணியின் வரிசை 2 × 3 மற்றும் B என்ற அணியின் வரிசை 3 × 3 என்பதால் AB என்ற அணி வரையறுக்கப்படுகிறது. மேலும் AB-யின் வரிசை 2 × 3 ஆகும்.

எடுத்துக்காட்டு 3.68 

If 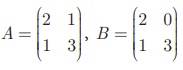எனில் AB மற்றும் BA காண்க. மேலும் AB = BA என்பது சரியா என ஆராய்க.

தீர்வு 

A என்ற அணியின் வரிசை 2 × 2. B என்ற அணியின் வரிசை 2 × 2 எனவே, 2 × 2 என்ற வரிசையுடைய AB என்ற அணி வரையறுக்கப்படுகிறது.

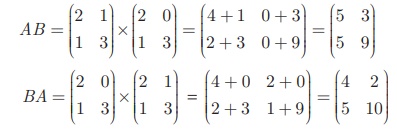
எனவே, AB ≠ BA. 

எடுத்துக்காட்டு 3.69 

எனில், அணியின் பெருக்கலைப் பொறுத்து A மற்றும் B என்ற அணிகளுக்குப் பரிமாற்று விதி உண்மை எனக் காட்டுக.

தீர்வு

AB = BA என நிரூபிக்க வேண்டும். 

எனவே, இடப்பக்கம் = வலப்பக்கம்

அதாவது, AB = BA

எடுத்துக்காட்டு 3.70 

தீர்க்க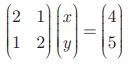 

தீர்வு

y = 2 என்பதை (1) -யில் பிரதியிட, 2x + 2 = 4 ⇒ x = 1 

எனவே, x = 1, y = 2

குறிப்பு 

• A, B என்பன இரண்டு பூச்சியம் இல்லா இரண்டு அணிகள் எனில் 

(A + B)2 ≠ A2 + 2AB + B2  

• ஆனால், AB = BA எனில், (A + B)2 = A2 + 2AB +B2 

எடுத்துக்காட்டு 3.71 

A = (1 -1 2), B = எனில் (AB)C = A(BC) எனக் காட்டுக. 

தீர்வு 

இடப்பக்கம் = (AB)C

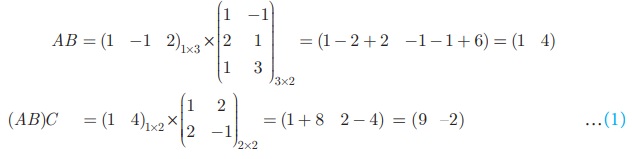
வலப்பக்கம் = A(BC) 

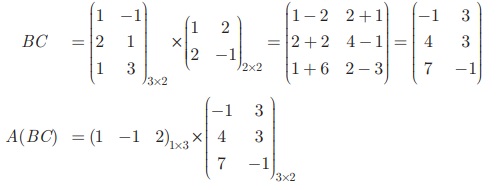
A (BC) = (−1 − 4 + 14 3 − 3 − 2) = (9−2) …(2)

(1) மற்றும் (2) லிருந்து, (AB)C = A(BC).

எடுத்துக்காட்டு 3.72 

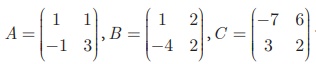எனில், A(B + C) = AB + AC. என்பதைச் சரிபார்க்க.

தீர்வு 

இடப்பக்கம் = A (B + C)

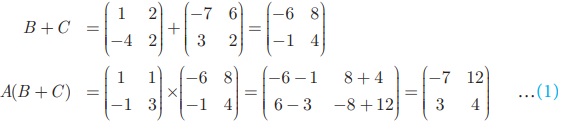
வலப்பக்கம் = AB + AC

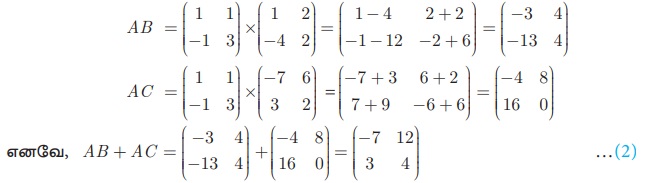
(1), (2) லிருந்து, A (B+ C) = AB+ AC என நிரூபிக்கப்பட்டது.

எடுத்துக்காட்டு 3.73 

எனில் (AB)T = BTAT என்பதைச் சரிபார்க்க.

தீர்வு 

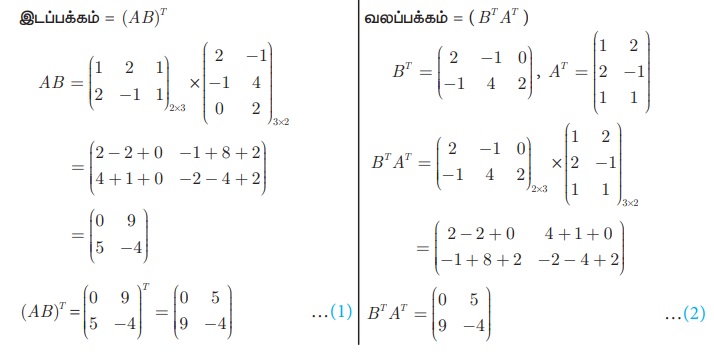
(1), (2) --லிருந்து (AB)T = B T AT என நிரூபிக்கப்பட்டது.