சமன்பாட்டைத் தீர்க்கும் படிகள், எடுத்துக்காட்டு - இருபடிச் சமன்பாடுகள் சார்ந்த கணக்குகளுக்குத் தீர்வு காணுதல் | 10th Mathematics : UNIT 3 : Algebra
10வது கணக்கு : அலகு 3 : இயற்கணிதம்
இருபடிச் சமன்பாடுகள் சார்ந்த கணக்குகளுக்குத் தீர்வு காணுதல்
இருபடிச் சமன்பாடுகள் சார்ந்த கணக்குகளுக்குத் தீர்வு காணுதல் (Solving Problems involving Quadratic Equations)
சமன்பாட்டைத் தீர்க்கும் படிகள்
படி 1 சொற்றொடர்களால் அமைந்த கணக்கை இருபடிச் சமன்பாடாக மாற்றுக.
படி 2 மேலே குறிப்பிட்ட மூன்று முறைகளில் ஏதேனும் ஒன்றைப் பயன்படுத்தி இருபடிச் சமன்பாட்டைத் தீர்க்க.
படி 3 கணித முறையில் பெற்ற விடையை வினாவிற்கு ஏற்ப சொற்றொடரில் மாற்றி எழுதுக.
எடுத்துக்காட்டு 3.36
குமரனின் தற்போதைய வயதின் இருமடங்கோடு ஒன்றைக் கூட்டினால் கிடைப்பது, குமரனின் இரண்டாண்டுகளுக்கு முந்தைய வயதையும் அவரின் 4 ஆண்டுகளுக்குப் பிந்தைய வயதையும் பெருக்கக் கிடைப்பதற்குச் சமம் எனில், அவரின் தற்போதைய வயதைக் காண்க.
தீர்வு
குமரனின் தற்போதைய வயது x ஆண்டுகள் என்க.
2 ஆண்டுகளுக்கு முன் வயது = (x - 2) ஆண்டுகள்.
4 ஆண்டுகளுக்குப் பின் வயது = (x + 4) ஆண்டுகள்.
கொடுத்த தகவல்படி, (x - 2) ( x + 4) = 1 + 2 x
x2 + 2 x – 8 = 1 + 2 x ⇒ (x - 3) (x + 3) = 0 ⇒ x = ±3
வயது குறை எண்ணாக இருக்க முடியாது.
எனவே, குமரனின் தற்போதைய வயது 3 ஆண்டுகள்.
எடுத்துக்காட்டு 3.37
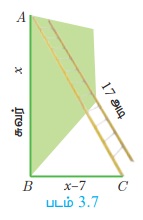
17 அடி நீளமுள்ள ஓர் ஏணி ஒரு சுவரின் மீது சாய்ந்துள்ளது. தரை, ஏணி மற்றும் செங்குத்துச் சுவர் மூன்றும் ஒரு செங்கோண முக்கோணத்தை உருவாக்குகின்றன. சுவரின் அடியிலிருந்து ஏணியின் அடி முனை வரை உள்ள தூரம் ஏணியின் மேல் முனை சுவரைத் தொடும் உயரத்தைவிட 7 அடி குறைவு எனில், சுவரின் உயரம் காண்க.
தீர்வு
சுவரின் உயரம் AB = x அடி என்க
கொடுக்கப்பட்ட தகவலின்படி BC = (x - 7) அடி
செங்கோண முக்கோணம் ABC, AC = 17 அடி BC = (x - 7) அடி
பித்தாகரஸ் தேற்றத்தின்படி, AC2 = AB2 + BC2
(17)2 = x2 + (x - 7)2; 289 = x2 + x2 – 14 x + 49
x2 − 7x −120 = 0 ⇒ (x - 15) (x + 8) = 0
ஆகவே, x = 15 அல்லது -8
உயரம் குறை எண்ணாக இருக்க இயலாது. எனவே, சுவரின் உயரம் 15 அடி ஆகும்.
எடுத்துக்காட்டு 3.38
ஓர் இடத்தில் x2 அன்னங்கள் கூட்டமாக இருந்தன. மேகங்கள் கூடியதால், 10x அன்னங்கள் ஏரிக்குச் சென்றன; எட்டில் ஒரு பங்கு தோட்டத்திற்குப் பறந்தன. மீதமுள்ள மூன்று ஜோடிகள் நீரில் விளையாடின எனில், மொத்த அன்னங்களின் எண்ணிக்கையைக் காண்க?
தீர்வு
மந்தையில் மொத்தம் x2 அன்னங்கள் உள்ளன. கொடுக்கப்பட்ட தகவல்களின்படி,
x2 − 10x – (1/8)x2 = 6 ⇒ 7x2 − 80x − 48 = 0
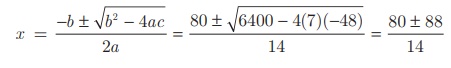
எனவே, x = 12, -4/7
அன்னங்களின் எண்ணிக்கை x = -4/7 ஆக இருக்க முடியாது.
ஆகையால், x = 12. மொத்த அன்னங்களின் எண்ணிக்கை x2 = 144 ஆகும்.
எடுத்துக்காட்டு 3.39
சென்னையிலிருந்து விருதாச்சலத்திற்கு 240 கி.மீ தூரத்தைக் கடக்க ஒரு பயணிகள் தொடர்வண்டிக்கு ஒரு விரைவு தொடர்வண்டியைவிட 1 மணி நேரம் கூடுதலாகத் தேவைப்படுகிறது. பயணிகள் தொடர்வண்டியின் வேகம், விரைவு தொடர்வண்டியின் வேகத்தைவிட 20 கி.மீ/மணி குறைவு எனில், இரு தொடர்வண்டிகளின் சராசரி வேகங்களைக் கணக்கிடுக.
தீர்வு
பயணிகள் தொடர்வண்டியின் சராசரி வேகம் x கி.மீ/மணி என்க.
தற்போது, விரைவு தொடர்வண்டியின் சராசரி வேகம் (x + 20) கி.மீ/மணி ஆகும்.
240 கி.மீ கடக்கப் பயணிகள் தொடர்வண்டி எடுக்கும் நேரம் = 240/x மணி
240 கி.மீ கடக்க விரைவு தொடர்வண்டி எடுக்கும் நேரம் = 240 / (x + 20) மணி
கொடுக்கப்பட்ட தகவல்களின்படி,
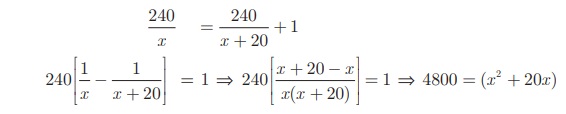
x2 + 20x – 4800 = 0 ⇒ (x + 80) (x − 60) = 0 ⇒ x = –80 or 60.
வேகம் ஒரு குறை எண்ணாக இருக்க முடியாது.
எனவே, பயணிகள் தொடர்வண்டியின் சராசரி வேகம் 60 கி.மீ/மணி எனவே, விரைவு தொடர்வண்டியின் சராசரி வேகம் 80 கி.மீ/மணி