Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕ, Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ, Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»ЂЯ«ЋЯ«│Я»Ї | Я«ЁЯ«│Я«хЯ«┐Я«»Я«▓Я»Ї | Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ - Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ»ЂЯ«▒Я«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ (Surface Area of Cuboid and Cube) | 9th Maths : UNIT 7 : Mensuration
9 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 7 : Я«ЁЯ«│Я«хЯ«┐Я«»Я«▓Я»Ї
Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ»ЂЯ«▒Я«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ (Surface Area of Cuboid and Cube)
Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ»ЂЯ«▒Я«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ (Surface Area of Cuboid and Cube)
Я««Я»ЂЯ«фЯ»ЇЯ«фЯ«░Я«┐Я««Я«ЙЯ«Б (3D) Я«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«єЯ«░Я««Я»ЇЯ«ф Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЋЯ«▒Я»ЇЯ«▒Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї. Я««Я»ЂЯ«┤Я»ЂЯ«хЯ«цЯ»ЂЯ««Я«ЙЯ«Ћ Я«њЯ«░Я»Ђ Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я«ЙЯ«ц Я«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«фЯ»ЇЯ«фЯ«░Я«┐Я««Я«ЙЯ«Б Я«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«еЯ»ЇЯ«цЯ«хЯ»іЯ«░Я»Ђ Я««Я»ЂЯ«фЯ»ЇЯ«фЯ«░Я«┐Я««Я«ЙЯ«Б Я«хЯ«ЪЯ«┐Я«хЯ««Я»ЂЯ««Я»Ї Я«еЯ»ђЯ«│Я««Я»Ї, Я«ЁЯ«ЋЯ«▓Я««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЅЯ«»Я«░Я««Я»Ї Я«јЯ«ЕЯ»ЇЯ«▒ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«фЯ«░Я«┐Я««Я«ЙЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
1. Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«фЯ»ЂЯ«▒Я«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ (Cuboid and its Surface Area)
Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ««Я»Ї : Я«њЯ«░Я»Ђ Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«єЯ«▒Я»Ђ Я«џЯ»єЯ«хЯ»ЇЯ«хЯ«Ћ Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я«ЙЯ«Е Я«цЯ«│Я«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«ЋЯ«│Я«ЙЯ«▓Я»Ї Я«ЁЯ«ЪЯ»ѕЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я««Я»ѓЯ«ЪЯ«┐Я«» Я«цЯ«┐Я«БЯ»ЇЯ«« Я«ЅЯ«░Я»ЂЯ«хЯ««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«цЯ»ђЯ«фЯ»ЇЯ«фЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐, Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ«▓Я»Ї, Я«фЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЋЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї
Я«џЯ«┐Я«▓ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї:
Я«њЯ«░Я»Ђ Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ««Я«ЙЯ«ЕЯ«цЯ»Ђ 6 Я««Я»ЂЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї, 12 Я«хЯ«┐Я«│Я«┐Я««Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 8 Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Ћ, Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ««Я«ЙЯ«ЕЯ«цЯ»Ђ Я«џЯ»єЯ«хЯ»ЇЯ«хЯ«Ћ Я«хЯ«ЪЯ«┐Я«хЯ«фЯ»Ї Я«фЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
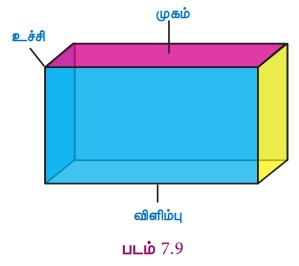
Я«њЯ«░Я»Ђ Я«ЋЯ«ЕЯ«џЯ»Ї Я«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ»ЂЯ«▒Я«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ (Total Surface Area РѕњTSA) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЁЯ«еЯ»ЇЯ«цЯ«ЋЯ»Ї Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ»ѕ Я««Я»ѓЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я««Я»ЂЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ЄЯ«▓Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«еЯ»ђЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ (Lateral Surface Area Рѕњ LSA) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
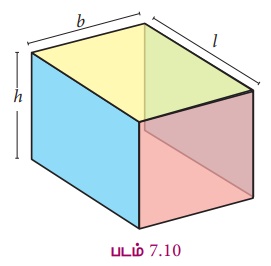
Я«фЯ«ЪЯ««Я»Ї 7.10 Я«ЄЯ«▓Я»Ї l,
b Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї
h Я«єЯ«ЋЯ«┐Я«»Я«Е Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є Я«еЯ»ђЯ«│Я««Я»Ї, Я«ЁЯ«ЋЯ«▓Я««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЅЯ«»Я«░Я«цЯ»ЇЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е.
(i) Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї
Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ (TSA)
Я««Я»ЄЯ«▓Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ 2 ├Ќ 1b
Я««Я»ЂЯ«ЕЯ»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ 2
├Ќ bh
Я«ЄЯ«ЪЯ«цЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«▓Я«цЯ»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ 2 ├Ќ lh

= 2 (lb + bh
+ lh) Я«џЯ«цЯ»ЂЯ«░
Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї.
(ii) Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї
Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ (LSA)
Я««Я»ЂЯ«ЕЯ»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ 2 ├Ќ bh
Я«ЄЯ«ЪЯ«цЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«▓Я«цЯ»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ 2
├Ќ lh

= 2 (l+b)h Я«џЯ«цЯ»ЂЯ«░ Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї.
Я«ЁЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«Ъ Я«хЯ«ЙЯ«┤Я»ЇЯ«хЯ«┐Я«»Я«▓Я»Ї Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«хЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«еЯ«ЙЯ««Я»Ї Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ (TSA) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ (LSA) Я«єЯ«ЋЯ«┐Я«» Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї.
Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я«еЯ»ђЯ«│Я««Я»Ї, Я«ЁЯ«ЋЯ«▓Я««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЅЯ«»Я«░Я«цЯ»ЇЯ«цЯ»ѕ Я«ЅЯ«ЪЯ»ѕЯ«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«Ћ Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я«ЙЯ«Е Я«ЊЯ«░Я»Ї Я«ЁЯ«▒Я»ѕЯ«»Я»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї.
Я«ЁЯ«еЯ»ЇЯ«ц Я«ЁЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«цЯ«░Я»ѕЯ«цЯ»ЇЯ«цЯ«│Я««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ»ѓЯ«░Я»ѕЯ«»Я»ѕЯ«цЯ»Ї Я«цЯ«хЯ«┐Я«░Я»ЇЯ«цЯ»ЇЯ«цЯ»ЂЯ«џЯ»Ї Я«џЯ»ЂЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я»єЯ«ЕЯ«┐Я«▓Я»Ї, Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»ѕЯ«ЋЯ»Ї (LSA) Я«ЋЯ«ЙЯ«Б Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї. Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«┤Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«▒Я«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»ѕЯ«»Я»ЂЯ««Я»Ї
Я«ЋЯ«ЙЯ«Б Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»єЯ«ЕЯ«┐Я«▓Я»Ї Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»ѕЯ«ЋЯ»Ї (TSA) Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«Ъ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.
Я«њЯ«░Я»Ђ Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї, Я«ЁЯ«ЋЯ«▓Я««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЅЯ«»Я«░Я««Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є l, b Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї h Я«јЯ«ЕЯ«┐Я«▓Я»Ї
(i) Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ = 2 (lb + bh + lh)
Я«џЯ«цЯ»ЂЯ«░ Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї.
(ii) Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ = 2 (l+b) h Я«џЯ«цЯ»ЂЯ«░ Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
Рђб Я«њЯ«░Я»Ђ Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«Ћ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЄЯ«▒Я»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«ЙЯ«ЕЯ«цЯ»Ђ Я«ЅЯ«»Я«░Я«цЯ»ЇЯ«цЯ»ІЯ«ЪЯ»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ«▓Я»ЇЯ«▓. Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«Ћ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЄЯ«▒Я»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 2lb Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ«ЙЯ«Е 2 (lb + bh
+ lh) Я«ЄЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 2lb Я«љ Я«еЯ»ђЯ«ЋЯ»ЇЯ«Ћ Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Рђб Я«њЯ«░Я»Ђ Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ»ЂЯ«▒Я«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ЂЯ««Я»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«еЯ»ђЯ«│Я««Я»Ї, Я«ЁЯ«ЋЯ«▓Я««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЅЯ«»Я«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«│Я«хЯ»ЂЯ«ЋЯ«│Я»Ї Я«њЯ«░Я»Є Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 7.4
Я«њЯ«░Я»Ђ Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї 7.5 Я««Я»ђ, Я«ЁЯ«ЋЯ«▓Я««Я»Ї 3 Я««Я»ђ, Я«ЅЯ«»Я«░Я««Я»Ї 5 Я««Я»ђ Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
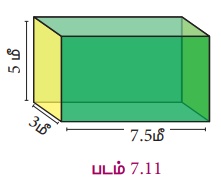
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ«ЕЯ«џЯ»Ї Я«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї (l) = 7.5 Я««Я»ђ , Я«ЁЯ«ЋЯ«▓Я««Я»Ї (b) = 3 Я««Я»ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЅЯ«»Я«░Я««Я»Ї (h) = 5 Я««Я»ђ.
Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ = 2 (lb + bh + lh)
= 2[(7.5 ├Ќ 3) + (3 ├Ќ
5) + (7.5 ├Ќ 5)]
= 2(22.5+15+37.5)
= 2 ├Ќ
75
= 150 Я««Я»ђ2
Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ = 2 (l+b)
├Ќ h
= 2(7.5 + 3) ├Ќ 5
= 2 ├Ќ
10.5 ├Ќ 5
= 105 Я««Я»ђ2
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 7.5
Я«ЊЯ«░Я»Ї Я«ЁЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї, Я«ЁЯ«ЋЯ«▓Я««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЅЯ«»Я«░Я««Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є 25 Я««Я»ђ, 15 Я««Я»ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 5 Я««Я»ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«цЯ«░Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«џЯ»ЂЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«фЯ»ЂЯ«цЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЋЯ»ЇЯ«Ћ 1 Я«џЯ«цЯ»ЂЯ«░ Я««Я»ђЯ«ЪЯ»ЇЯ«ЪЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Рѓ╣
80 Я«хЯ»ђЯ«цЯ««Я»Ї
Я«џЯ»єЯ«▓Я«хЯ»Ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я««Я»іЯ«цЯ»ЇЯ«цЯ«џЯ»Ї Я«џЯ»єЯ«▓Я«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ

Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї (l) = 25 Я««Я»ђ, Я«ЁЯ«ЋЯ«▓Я««Я»Ї (b) =15 Я««Я»ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЅЯ«»Я«░Я««Я»Ї (h) = 5 Я««Я»ђ Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«џЯ»ЂЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ = Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ
= 2 (l+b) ├Ќ h
= 2(25+15) ├Ќ 5
= 80 ├Ќ
5 = 400 Я«џ.Я««Я»ђ
Я«цЯ«░Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ = l ├Ќ b
= 25 ├Ќ
15
= 375 Я«џ.Я««Я»ђ
Я«фЯ»ЂЯ«цЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«» Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ = (Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«џЯ»ЂЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ + Я«цЯ«░Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ)
= (400+375) = 775 Я«џ.Я««Я»ђ
1 Я«џЯ«цЯ»ЂЯ«░
Я««Я»ђЯ«ЪЯ»ЇЯ«ЪЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Рѓ╣80 Я«хЯ»ђЯ«цЯ««Я»Ї Я«ЁЯ«▒Я»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ»ЂЯ«цЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЋЯ»ЇЯ«Ћ Я«єЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»іЯ«цЯ»ЇЯ«цЯ«џЯ»Ї Я«џЯ»єЯ«▓Я«хЯ»Ђ = 80 ├Ќ 775
= Рѓ╣ 62,000
2. Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«фЯ»ЂЯ«▒Я«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ (Cube and its Surface Area)
Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я««Я»Ї (Cube): Я«еЯ»ђЯ«│Я««Я»Ї, Я«ЁЯ«ЋЯ«▓Я««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЅЯ«»Я«░Я««Я»Ї Я«єЯ«ЋЯ«┐Я«» Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я«џЯ««Я««Я«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ««Я»Є, Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я««Я«ЙЯ«ЕЯ«цЯ»Ђ Я«єЯ«▒Я»Ђ Я«џЯ«цЯ»ЂЯ«░Я«фЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«▓Я»Ї Я«ЁЯ«ЪЯ»ѕЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ«┐Я«БЯ»ЇЯ««Я««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«┐Я«▓ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї:

Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»ІЯ«▓Я«хЯ»Є, Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я««Я»ЂЯ««Я»Ї 6 Я««Я»ЂЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї, 12 Я«хЯ«┐Я«│Я«┐Я««Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 8 Я«ЅЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
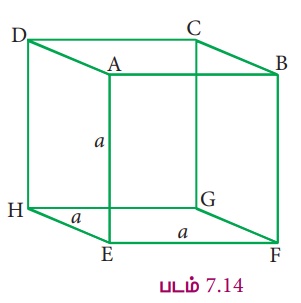
Я«фЯ«ЪЯ««Я»Ї 7.14 Я«ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ a
Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«фЯ«ЋЯ»ЇЯ«Ћ Я«ЁЯ«│Я«хЯ»Ђ Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«њЯ«░Я»Ђ Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЂЯ«хЯ»ІЯ««Я»Ї. Я«ЄЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ
Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ =
(ABCD+EFGH+AEHD+BFGC+ABFE+CDHG)
Я«єЯ«ЋЯ«┐Я«» Я««Я»ЂЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї =
(a2 + a2 + a2 + a2
+ a2 + a2)
= 6a2 Я«џЯ«цЯ»ЂЯ«░ Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї
(iii) Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї
Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ
= (AEHD+BFGC+ABFE+CDHG) Я«єЯ«ЋЯ«┐Я«» Я««Я»ЂЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї
= (a2 + a2 +
a2 + a2 )
= 4a2 Я«џЯ«цЯ»ЂЯ«░ Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї
Я«њЯ«░Я»Ђ Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«Ћ Я«ЁЯ«│Я«хЯ»Ђ a Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї,
(i) Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ (TSA) = 6a2
Я«џЯ«цЯ»ЂЯ«░ Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї
(ii) Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ (LSA) = 4a2
Я«џЯ«цЯ»ЂЯ«░ Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї
Я«џЯ«┐Я«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«│Я««Я»Ї
Я«ЄЯ«цЯ«ЕЯ»ЂЯ«ЪЯ«ЕЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»ЂЯ«ЪЯ»ѕЯ«» Я«ЋЯ«ЕЯ«џЯ»Ї Я«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«ЄЯ«еЯ»ЇЯ«цЯ«џЯ»Ї Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒ Я««Я»ЂЯ«ЪЯ«┐Я«»Я»ЂЯ««Я«Й?
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 7.6
5 Я«џЯ»єЯ««Я»ђ
Я«фЯ«ЋЯ»ЇЯ«Ћ Я«ЁЯ«│Я«хЯ»Ђ Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
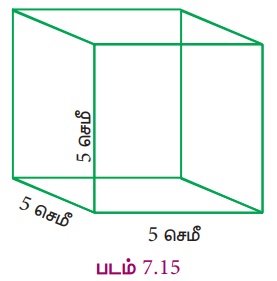
Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«Ћ Я«ЁЯ«│Я«хЯ»Ђ (a) = 5 Я«џЯ»єЯ««Я»ђ
Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ = 6a2
= 6(52) = 150 Я«џ.Я«џЯ»єЯ««Я»ђ
Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ = 4a2
= 4(52) = 100 Я«џ.Я«џЯ»єЯ««Я»ђ
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 7.7
Я«њЯ«░Я»Ђ Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ»ЂЯ«▒Я«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ
486 Я«џЯ»єЯ««Я»ђ2
Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ»ЂЯ«▒Я«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ
= 486 Я«џЯ»єЯ««Я»ђ2
6a2 = 486 ==> a2
= 486 / 6 , a2 = 81
==> a = 9
Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«Ћ Я«ЁЯ«│Я«хЯ»Ђ = 9 Я«џЯ»єЯ««Я»ђ
Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ = 4a2 = 4 ├Ќ 92 = 4 ├Ќ
81 = 324 Я«џЯ»єЯ««Я»ђ2
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 7.8
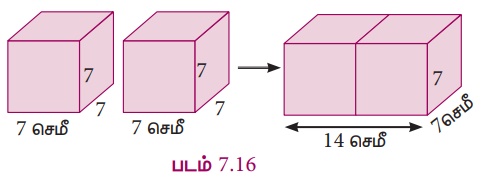
7 Я«џЯ»єЯ««Я»ђ
Я«фЯ«ЋЯ»ЇЯ«Ћ Я«ЁЯ«│Я«хЯ»ЂЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Є Я««Я«ЙЯ«цЯ«┐Я«░Я«┐Я«»Я«ЙЯ«Е Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»ЂЯ«ЪЯ«ЕЯ»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«хЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«цЯ«┐Я«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«Ћ Я«ЁЯ«│Я«хЯ»Ђ = 7 Я«џЯ»єЯ««Я»ђ
Я«фЯ»ЂЯ«цЯ«┐Я«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї (l) = 7+7 =14 Я«џЯ»єЯ««Я»ђ
Я«ЁЯ«ЋЯ«▓Я««Я»Ї (b) = 7 Я«џЯ»єЯ««Я»ђ, Я«ЅЯ«»Я«░Я««Я»Ї (h) = 7 Я«џЯ»єЯ««Я»ђ
Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ = 2 (lb
+ bh + lh)
= 2[(14├Ќ7)
+ (7├Ќ7) + (14├Ќ7)]
= 2(98+ 49+98)
=2 ├Ќ
245
= 490 Я«џЯ»єЯ««Я»ђ2
Я«фЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»Ђ = 2 (l+b) ├Ќ h
= 2(14+7) ├Ќ 7
= 2 ├Ќ
21 ├Ќ 7
= 294 Я«џЯ»єЯ««Я»ђ2