இயற்கணிதக் கோவையை மரவுரு வரைபடமாக மாற்றுதல்

இயற்கணிதக் கோவையை மரவுரு வரைபடமாக மாற்றுதல்

மரவுரு வரைபடத்தில் மேலும் பல செயல்பாடுகளைக் காணலாம். பின்வரும் மரவுரு வரைபடத்தை உற்றுநோக்குக.

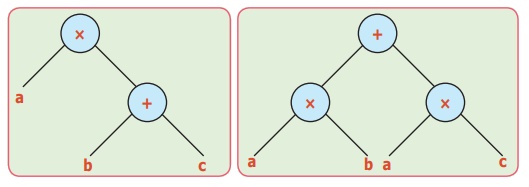
மேற்காணும் மரவுரு வரைபடமானது நாம் அறிந்த சமன்பாடே ஆகும். a × (b + c) = (a ×  b) + (a ×  c).

இது போன்ற இயற்கணிதச் சமன்பாடுகளையும் மரவுரு வரைபடத்தில் எளிதில் காணலாம். 

1) இடது பக்கம் உள்ள மரவுரு வரைபடத்தில் குறைந்த எண்ணிக்கையில் கணுக்கள் உள்ளன இது பார்ப்பதற்கும் எளிதாக உள்ளது.

2) வலது பக்கம் உள்ள மரவுரு வரைபடத்தில் அதிக எண்ணிக்கையில் கணுக்கள் உள்ளன. 

3) கொடுக்கப்பட்ட இரண்டு மரவுரு வரைபடங்களின் மதிப்புகள் வெவ்வேறானவை என்ற முடிவுக்கு நம்மால் வர இயலுமா?

எ.கா. 15: 5a ஐ மரவுரு வரைபடமாக மாற்றுக

தீர்வு:

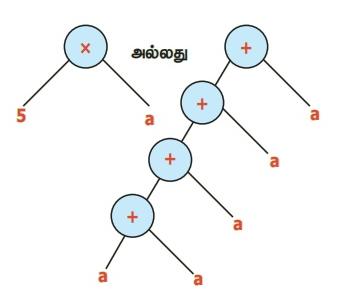
எ.கா. 16: 3a + b ஐ மரவுரு வரைபடமாக மாற்றுக

தீர்வு:

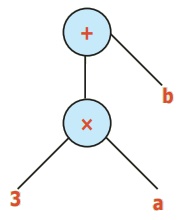
இயற்கணிதக் கோவை

3a + b

மரவுரு வரைபடம்

எ.கா. 17: a இன் 6 மடங்கிலிருந்து 7 குறைவு. இதனை மரவுரு வரைபடமாக மாற்றுக.

தீர்வு:

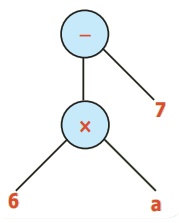
இயற்கணிதக் கோவை

6a –7

மரவுரு வரைபடம்

எ.கா. 18: கீழே கொடுக்கப்பட்ட மரவுரு வரைபடத்தை இயற்கணிதக் கோவையாக எழுதுக

தீர்வு:

மரவுரு வரைபடம்

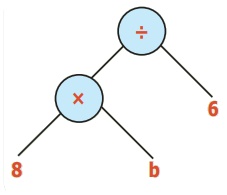
இயற்கணிதக் கோவை

8b ÷ 6

எ.கா. 19: கொடுக்கப்பட்ட மரவுரு வரைபடத்தை இயற்கணிதக் கோவையாக மாற்றுக.

தீர்வு:

மரவுரு வரைபடம்

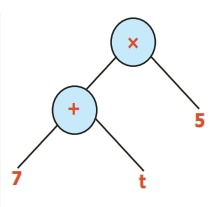
இயற்கணிதக் கோவை

(7 + t)5

எ.கா. 20: கொடுக்கப்பட்ட மரவுரு வரைபடத்தின் மதிப்புகள் சமமா அல்லது இல்லையா எனச் சரிபார்க்க

தீர்வு:

மரவுரு வரைபடம்

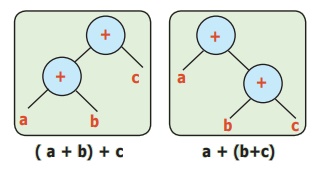
 ( a + b) + c = a + (b+c)

ஆம். இவைகள் இரண்டும் சமம்

இவற்றை முயல்க

1) பின்வரும் மரவுரு வரைபடங்கள் சமமா ? இல்லையா? என ஆராய்க.

(i)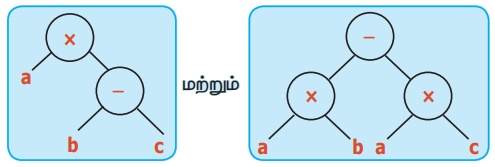

விடை:

a × (b−c) = ab – ac = (a×b) – (a×c) 

சமம்

(ii)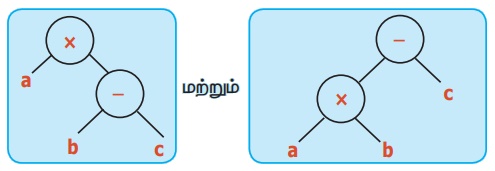

 a × (b−c) = ab – ac = (a×b) – (a×c) ≠ (a×b) − c

சமம்இல்லை

2) பின்வரும் இயற்கணிதக் கோவைகள் சமமா? இல்லையா? என்பதை மரவுரு வரைபடம் மூலம் சரிபார்க்க.

அ) (x – y) + z மற்றும் x – (y + z)

விடை:

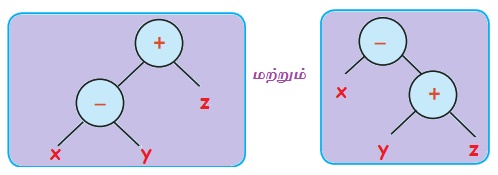
சமம்

ஆ) (p × q) × r மற்றும் p × (q × r)

விடை:

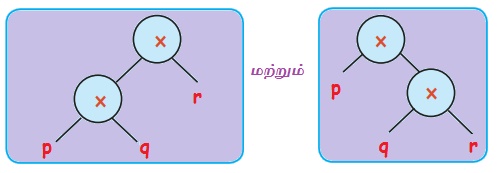
சமம்

இ) a – (b – c) மற்றும் (a – b) – c

விடை:

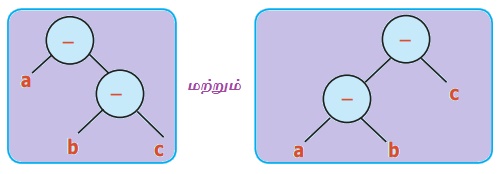
சமம்

உங்களுக்குத் தெரியுமா?

9 – 4 என்ற எண்கோவையை எடுத்துக் கொள்க. அதாவது 9லிருந்து 4 ஐக் கழிக்க என இதன் பொருள்படும். 9 – 4 ஐ – 94 என எழுதலாம். (இதுவரை இரண்டு எண்களுக்கு இடையில் குறியீடுகளைக் கொண்டு வருதல் பற்றித் தெரிந்துள்ளோம்).

9 – 4 × 2 என்ற கோவையை × – 9 4 2 என எழுதலாம். இதனைப் பின்வரும் படிகளைக் கொண்டு விளக்கலாம்.

படி.1 : × 9 – 4  2

படி.2: ( 9 – 4 )  × 2

+ × – 9 4 2 5 என்ற கோவையை எடுத்துக்கொள்வோம்.

படி.1 : + × 9 – 425 

படி.2 : + ( 9 – 4 ) × 2 5 

படி.3: [ (9 – 4)  × 2] 5

இடமிருந்து வலமாக இக்கோவையைப் படிக்கின்றோம். இதே போல் வலமிருந்து இடமாகவும் படிக்கலாம்.

9 4 2 5 + × – ஐ வலமிருந்து இடமாகப் படிக்கும்போது பின்வரும் விளக்கத்தைக் கொடுக்கிறது. 

 9 4 2 5 + × – => (9 – 4) 2 5 + ×

=> (9 – 4) × 2 5 + 

=> [(9 – 4) × 2] + 5

4 என்ற எண்ணைத் தமிழில் நான்கு எனவும் ஆங்கிலத்தில் four எனவும் இந்தியில் (சார்) எனவும் தெலுங்கில் (நாலுகு) எனவும் கூறுவதைப் போலவே, ஒரு கோவையை இடமிருந்து வலமாகவோ அல்லது வலமிருந்து இடமாகவோ செயலிகளைப் பயன்படுத்தி, ஒரே விடையைப் பெறலாம்.

[(9 – 4) × 8] ÷ [(8 + 2) × 3] என்ற எண் கோவையை  ÷ × 9 4 8 × + 8 2 3 (இடமிருந்து வலம்) அல்லது 

 8 9 4 – × 3 8 2 + × ÷ (வலமிருந்து இடம்) என எழுதலாம்.

இவற்றை முயல்க

 i) × – + 9 7 8 2 

 ii) + × + 2 3 8 5