இயக்கச் சமன்பாடுகள்

இயக்கச் சமன்பாடுகள்

நியூட்டன், ஒரு பொருளின் இயக்கத்தை ஆய்வு செய்ததன் விளைவாக மூன்று சமன்பாடுகளின் தொகுப்பை வழங்கினார். இந்த சமன்பாடுகள் இயக்கத்தில் இருக்கும் ஒரு பொருளின் இடப்பெயர்ச்சி, திசைவேகம், முடுக்கம் மற்றும் நேரம் ஆகியவற்றிற் கிடையேயான தொடர்பினைக் கூறுகின்றன. a என்ற முடுக்கத்தினால் இயங்கும் பொருள் ஒன்று t' காலத்தில் 'u' என்ற தொடக்க திசை வேகத்திலிருந்து ‘v' என்ற இறுதித் திசைவேகத்தை அடைகிறது. அப்போது அதன் இடப்பெயர்ச்சி 'S' எனில் இயக்கச் சமன்பாடுகளை கீழ்க்கண்டவாறு எழுதலாம்.

v = u + at

 S = ut + 1/2 a t2

v² = u² + 2as

இயக்கத்தில் இருக்கும் ஒரு பொருளுக்கு வரைபட முறையின் மூலம் இந்த சமன்பாடுகளைப் பெற முடியும்.

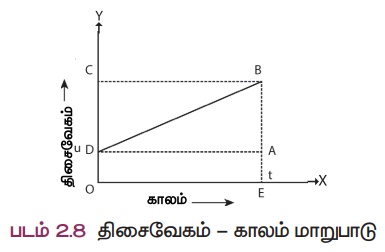
மேற்கண்ட வரைபடம் சீராக முடுக்கப்பட்ட பொருள் ஒன்று காலத்தைப் பொறுத்து அடையும் திசைவேக மாற்றத்தைக் காண்பிக்கிறது. வரைபடத்தில் 'D' என்ற தொடக்கப் புள்ளியிலிருந்து 'u' என்ற திசை வேகத்துடன் இயங்கும் பொருளொன்றின் திசைவேகம் தொடர்ச்சியாக அதிகரித்து t காலத்திற்குப் பின் 'B' என்ற புள்ளியை அப்பொருள் அடைகிறது.

பொருளின் தொடக்க திசைவேகம் = u = OD = EA

பொருளின் இறுதித் திசைவேகம் = v = OC = EB

காலம் = t = OE = DA

 வரைபடத்திலிருந்து AB = DC ஆகும்.

முதல் இயக்கச் சமன்பாடு

வரையறைப்படி முடுக்கம் (a)

= திசைவேக மாறுபாடு/காலம்

= (இறுதித் திசைவேகம் - தொடக்கத் திசைவேகம்) / காலம்

at = (OC-OD)/ OE =  DC/ OE = DC/t          

DC = at= AB

வரைபடத்திலிருந்து, EB = EA + AB

v = u + at     (1)

இது முதல் இயக்கச் சமன்பாடு ஆகும்.

இரண்டாம் இயக்கச் சமன்பாடு

வரைபடத்திலிருந்து, 't' காலத்தில் பொருள் ஒன்று கடந்த தொலைவான நாற்கரத்தின் பரப்பளவு DOEB மூலம் கொடுக்கப்படுகிறது.

S = நாற்கரத்தின் பரப்பளவு DOEB

= செவ்வகத்தின் பரப்பளவு DOEA + முக்கோணத்தின் பரப்பளவு DAB

= ( AE× OE ) + 1/2 × (AB × DA)

S = ut + 1/2 at²       (2)

இது இரண்டாம் இயக்கச் சமன்பாடு ஆகும்.

மூன்றாவது இயக்கச் சமன்பாடு

t' காலத்தில் பொருள் கடந்த தொலைவை வரைபடத்தில் நாற்கரம் DOEB யின் பரப்பளவானது குறிக்கிறது. இங்கு DOEB என்பது சரிவகத்தையும் குறிக்கிறது.

S = சரிவகம் DOEB யின் பரப்பளவு

= 1/2 × இணைப் பக்க நீளங்களின் கூடுதல் × இணைப் பக்கங்களுக்கு இடைப்பட்ட தொலைவு

= 1/2 × (OD + BE) × OE

S = 1/2 × (u + v) × t

ஆனால், முடுக்கம் a = (v - u) / t அல்லது

t = (v - u)/a

எனவே , s = 1/2 × (v + u) × (v - u)/a

2as = v² - u²

v² = u² + 2as       (3)                                        

இது மூன்றாம் இயக்கச் சமன்பாடு ஆகும்.

கணக்கீடு 3

மகிழுந்து ஒன்றில் வேகத்தடையைப் பயன்படுத்தும் போது, 6 மீ / விநாடி² முடுக்கத்தை அது செல்லும் திசைக்கு எதிர்த்திசையில் ஏற்படுத்துகிறது. நிறுத்தக் கருவியைப் (brake) பயன்படுத்திய பிறகு 2 விநாடி கழித்து மகிழுந்து நின்றது. இக்கால இடைவெளியில் அது கடந்த தொலைவைக் கணக்கிடுக.

தீர்வு

கொடுக்கப்பட்ட தகவல்கள்

முடுக்கம் a =-6 மீ / விநாடி²

காலம் t = 2 விநாடி

இறுதிவேகம் v = 0

இயக்கச் சமன்பாட்டிலிருந்து, v = u + at

0 = u + (-6×2)

0 = u – 12

 u = 12 மீ / விநாடி

S = ut + 1/2 at²

= [(12× 2) + 12 (-6×2× 2)]

S = 24 - 12 = 12

 S= 12 மீ

நிறுத்தக் கருவியைப் (brake) பயன்படுத்திய பின்னர் மகிழுந்து ஓய்வு நிலைக்கு வருவதற்குள் அது 12 மீ தொலைவைக் கடந்திருக்கும்.

தடையின்றி தானே விழும் பொருளின் இயக்கம்

 செயல்பாடு 4

ஒரு பெரிய கல் மற்றும் சிறிய அழிப்பான் இரண்டையும் எடுத்துக் கொள்க. ஒரு மேசையின் மீது நின்று கொண்டு அந்த இரண்டு பொருட்களையும் ஒரே உயரத்திலிருந்து ஒரே நேரத்தில் கீழே விடவும். நீங்கள் காண்பது என்ன? இப்பொழுது, ஒரு சிறிய அழிப்பான் மற்றும் ஒரு காகிதத் தாள் இரண்டையும் எடுத்துக்கொள்க. ஒரு மேசையின் மீது நின்று கொண்டு அந்த இரண்டு பொருட்களையும் ஒரே உயரத்திலிருந்து ஒரே நேரத்தில் கீழே விடவும். என்ன காண்கிறீர்கள்? இப்பொழுது, சமமான நிறையுடைய இரண்டு காகிதத் தாள்களை எடுத்துக் கொள்க. இதில் ஒன்றை மட்டும் கசக்கி பந்து போல் சுருட்டிச் கொள்க. இப்பொழுது இரண்டையும் ஒரே உயரத்தில் இருந்து ஒரே நேரத்தில் கீழே விடவும். இப்பொழுது என்ன நடைபெறுகிறது? நீங்கள் காண்பது என்ன?

செயல்பாடு 4-ல், கல் மற்றும் அழிப்பான் இரண்டும் பூமியின் மேல்பரப்பை சற்றேறக்குறைய ஒரே நேரத்தில் வந்தடைந்தன என்பதைக் காண முடியும். ஆனால், அழிப்பானையும், காகிதத்தையும் கீழே விடும் பொழுது அழிப்பான் முதலில் வந்தடைகிறது. காகிதத்தாள் பின்னர் வந்தடைகிறது. அதைப்போலவே காகிதத்தாளும், பந்துபோல் சுருட்டப்பட்ட காகிதமும் ஒரே எடையைப் பெற்றிருந்த போதும், பந்து போல் சுருட்டப்பட்ட காகிதம் முதலாவதும், காகிதத் தாள் இரண்டாவதும் தரையை வந்தடைவதைக் காணலாம். இதற்கான காரணம் உங்களுக்குத் தெரியுமா? காற்றில்லாத வெற்றிடத்தில் மேற்சொன்ன அனைத்துப் பொருட்களும் ஒரே நேரத்தில் தரையை வந்தடையும். காற்று ஊடகத்தில் காற்றின் உராய்வு விசையானது தடையின்றி தானே விழும் பொருளின் மீது ஒரு தடையை ஏற்படுத்துகிறது.

அழிப்பான் மற்றும் கல்லின் மீது செயல்படும் இந்த காற்றுத்தடை புவிஈர்ப்பு விசையுடன் ஒப்பிடும்போது புறக்கணிக்கத் தக்கதாகும். எனவே அவையிரண்டும் ஏறத்தாழ ஒரே நேரத்தில் தரையை வந்தடைகின்றன. இந்த செயல்பாடுகளின் மூலம், காற்றுத் தடையின் அளவானது, பொருளின் பரப்பளவைப் பொறுத்துள்ளது என்பதை அறியலாம்.

தடையின்றி கீழே விழும் பொருட்கள் முடுக்கமடையும் என்பது நமக்குத் தெரிந்ததே. இந்த முடுக்கம் பொருளின் நிறையைப் பொருத்தது அல்ல. அதாவது, உள்ளீடற்ற பொருள் அல்லது திடப்பொருள் மற்றும் சிறிய அல்லது பெரிய பொருட்கள் அனைத்தும் ஒரே கால வீதத்தில் கீழே விழும். முடுக்கம் ‘a’ க்குப் பதிலாக புவிஈர்ப்பு முடுக்கம் 'g' ஐப் பிரதியிடுவதால், தடையின்றி தானே கீழே விழும் பொருட்களுக்கான சமன்பாடுகளைப் பெற முடியும். தடையின்றி தானே விழும் பொருட்களுக்கு அதன் ஆரம்பத் திசைவேகம் u = 0. எனவே, கீழ்க்காணும் சமன்பாடுகளைப் பெற முடியும்.

v = gt, s = 1/2 gt², v² = 2gh

உங்களுக்குத் தெரியுமா?

ஒரு பொருள் சுழி திசைவேகம் மற்றும் வரையறுக்கப்பட்ட முடுக்கத்தைக் கொண்டிருக்க முடியுமா? ஆம், ஒரு பொருளை செங்குத்தாக மேல்நோக்கி எறிந்தால், பொருளின் திசைவேகம் படிப்படியாகக் குறைந்து, பெரும உயரத்தை அடைந்த நிலையில் சுழி மதிப்பைப் பெறுகிறது. அப்போது அப்பொருளின் முடுக்கம் புவிஈர்ப்பு முடுக்கத்துக்குச் சமமாக இருக்கும்.

ஒரு பொருளை மேல்நோக்கி எறியும் பொழுது அது, புவியீர்ப்பு விசைக்கு எதிர்த்திசையில் செல்கிறது. எனவே, a க்கு பதிலாக -g என்றும் எடுத்துக்கொள்ள வேண்டும். கீழ்நோக்கிச் செல்லும்போது, +g என எடுத்துக்கொள்ள வேண்டும்.

சீரான வட்ட இயக்கம்

செயல்பாடு 5

ஒரு நூலை எடுத்துக்கொண்டு, அதன் ஒரு முனையில் சிறிய கல் ஒன்றைக் கட்டவும். அக்கல்லானது வட்டப்பாதையில் மாறாத வேகத்தில் சுற்றுமாறு கயிற்றின் மற்றொரு முனையைக் கொண்டு சுழற்றவும். நூலைக் கையிலிருந்து விடுவிக்கும் போது கல்லானது விலகிச் செல்கிறது. கயிற்றை விடுவித்த பின்பு கல்லானது எந்தத் திசையில் செல்லும் என்பதை உங்களால் சொல்ல முடியுமா?

நீங்கள் உன்னிப்பாக நோக்கினால் கயிற்றை விடுவிக்கும் போது கல்லானது வட்டப்பாதையின் தொடுகோட்டின் வழியே நேர்கோட்டில் இயங்கு வதைக் காணலாம். ஏனெனில் கல்லை விடுவிக்கும் காலத்தில் அதனை எத்திசையில் விடுவித்தோமோ அதே திசையில் சென்று கொண்டிருக்கும். இது, ஒரு பொருள் வட்ட வடிவப் பாதையில் செல்லும்போது அதன் திசை ஒவ்வொரு புள்ளியிலும் மாறிக் கொண்டே இருக்கும் என்பதைக் காட்டுகிறது.

பொருள் ஒன்று வட்டப்பாதையில் மாறாத வேகத்தில் செல்லும் பொழுது, திசை மாறுவதால், திசைவேகமும் மாறுகின்றது. எனவே, இது ஒரு முடுக்குவிக்கப்பட்ட இயக்கமாகும். உதாரணமாக, பூமி சூரியனைச் சுற்றி வருவது, நிலவு பூமியைச் சுற்றி வருவது, கடிகாரத்தின் வினாடி முள்ளின் இயக்கம் ஆகியவை சீரான வட்ட இயக்கங்களாகும்.

'r' ஆரம் கொண்ட வட்டப் பாதையில் சுற்றிவரும் ஒரு பொருளானது, ஒரு சுற்றுக்குப்பின் தொடக்க நிலைக்கு திரும்பிவர எடுத்துக்கொண்ட காலம் 'T' எனில் அதன் வேகம் 'V' பின்வருமாறு கணக்கிடப்படுகிறது.

வேகம் V = சுற்றளவு/எடுத்துக்கொண்ட காலம்

V = 2πr/T