தகவல் செயலாக்கம்

இயல் 5

தகவல் செயலாக்கம்

கற்றல் நோக்கங்கள்:

● எண் கோவை மற்றும் இயற்கணிதக் கோவையை மரவுரு வரைபடத்தில் குறிப்பிடுதல் 

● மரவுரு வரைபடத்திலிருந்து எண் கோவை மற்றும் இயற்கணிதக் கோவையை எழுதுதல்.

அறிமுகம்

இன்றைய தொழில்நுட்ப காலகட்டத்தில் கணினி இல்லாத ஒரு நாளை கற்பனை செய்து கூடப் பார்க்க இயலாது. சிறிய கடைகள் முதல் மிகப் பெரிய மென்பொருள் நிறுவனங்கள் வரை கணினியின் பயன்பாடு தவிர்க்க முடியாததாகிறது. கணினி இல்லையெனில் அனைத்துச் செயல்பாடுகளும் பெருமளவில் முடங்கிவிடும். கணினியானது மிகவும் கடினமான மற்றும் சிக்கலான எண் கோவைகளையும் இயற்கணிதக் கோவைகளையும் எளிமையாகத் தீர்த்து விடைகளை மிகக் குறுகிய நேரத்தில் கொடுத்து விடும். அவ்விடைகள் மிகவும் துல்லியமாகவும் மீண்டும் கணக்கிட வேண்டியத் தேவை இல்லாமலும் இருக்கும். கணினி நாம் கொடுக்கும் கோவைகளை எவ்வாறு எடுத்துக்கொள்ளும் என்ற வினா நமக்குள் எழுகின்றதல்லவா?

ஆம். மரவுரு வரைபடம் முறையில் கணினியானது பில்லியன் செயல்பாடுகளை ஒரே நேரத்தில் சீரான முறையில் கணக்கிட்டு நமக்கு விடைகளைக் கொடுக்கின்றது. இந்த இயலில் எண் கோவை மற்றும் இயற்கணிதக் கோவை இரண்டையும் எவ்வாறு மரவுரு வரைபடத்தில் குறிப்பிடலாம் என்பதைப் பற்றி கற்றுக் கொள்வோம்.

எங்கும் கணிதம்–அன்றாட வாழ்வில் தகவல் செயலாக்கம்

மனித மூளையில் தகவல் செயலாக்கம்

கணினியில் தகவல் செயலாக்கம்

[(9 – 4) × 8] ÷ [(8 + 2) × 3] என்ற எண் கோவையை எடுத்துக் கொள்க. மரவுரு வரைபடம் வழியாக கோவைகளை நன்றாக புரிந்து கொள்ளலாம்.

1) e1 = (9 – 4) × 8 மற்றும் e2 = (8 + 2) × 3 எனவும் எடுத்துக்கொள்க

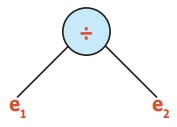
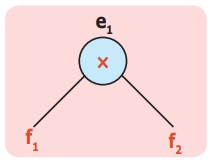
2) e1 = f1 × f2

இங்கு f1 = 9 – 4 மற்றும் f2 = 8

3) f1 = r1 – r2 இங்கு r1 = 9 மற்றும் r2 = 4.

f1 ஐப் பின்வருமாறு எழுதலாம்.

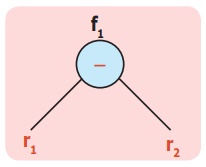
இதைப் போன்றே மரவுரு வரைபடம் மூலம் e2 வையும் குறிப்பிடலாம்.

4) இவை அனைத்தையும் ஒன்றாக இணைத்தால் நமக்குப் பின்வரும் மரவுரு வரைபடம் கிடைக்கின்றது.

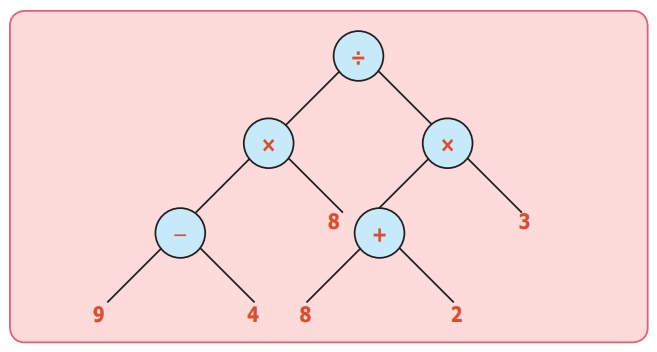
மேற்கண்ட படமானது பார்ப்பதற்கு தலைகீழாக வளரும் மரவுருவத்தைப் போல் தோன்றும். இரண்டு கிளைகள் இணையும் பகுதி கணு ஆகும். ஒவ்வொரு கணுவிலும் ஒன்று அல்லது இரண்டு கிளைகள் இருக்கும். ஒவ்வொரு கணுவிலும் கணிதக் குறியீடுகளையும் கிளைகளில் எண்களையும் எழுதிப் படம் வரைந்தால் மரவுரு வரைபடம் நமக்குக் கிடைக்கின்றது. மரவுரு வரைபடம் எண் கோவையைக் குறிக்கும் பொதுவான வழியாகும். இங்கு மரவுருவங்கள் தலைகீழாக வரையப்படுகின்றது.

வேர் மேலாகவும் கிளைகள் கீழாகவும் உள்ளது. கணிதச் செயல்பாடுகள் அனைத்தும் இருமச் செயல்பாட்டினைக் கொண்டுள்ளதால் பெரும்பாலும் இரு கிளைகள் கொண்ட மரவுரு வரைபடம் மட்டுமே உள்ளது.

நான்கு எண்களைக் கூட்டல் குறியீட்டில் இதே போல் எழுதலாமா? ஆம். மரவுரு வரைபடத்தில் 4 எண்களின் கூடுதலை இவ்வாறு எழுதலாம்.

வாக்கியக் கணக்குகளை மரவுரு வரைபடத்தில் எவ்வாறு குறிப்பிடலாம் என்பதனைக் கற்போம்

எ.கா 1: ஊட்டியில் நடைபெற்ற பூக்கண்காட்சியில் முதல், இரண்டு, மூன்று மற்றும் நான்காவது நாட்களில் விற்ற நுழைவுச் சீட்டுகள் முறையே 1,10,010, 75,070, 25,720 மற்றும் 30,636 ஆகும். 4 நாட்களிலும் மொத்தமாக விற்பனை செய்யப்பட்ட மொத்த நுழைவுச் சீட்டுகள் எத்தனை ?

தீர்வு:

எ.கா 2 : ஒரு காகித விற்பனை நிறுவனம் தன்னுடைய இருப்பில் உள்ள 7,50,800 குறிப்பேடுகளில் 6,25,610 குறிப்பேடுகளை ஓர் ஆண்டில் விற்பனை செய்துள்ளது எனில் அந்நிறுவனத்தில் விற்பனை ஆகாத குறிப்பேடுகளின் எண்ணிக்கையைக் காண்க.

தீர்வு:

எ.கா 3 : வாணி, கலா மற்றும் அவர்களுடைய மூன்று தோழிகள் மோர் கடைக்குச் சென்றனர். மேலும் 9 தோழிகள் அவர்களுடன் இணைந்து மோர் குடித்தனர். ஒரு குவளை மோரின் விலை ₹6 எனில், வாணி எவ்வளவு தொகை கொடுத்திருப்பாள்? வாணி ₹84 கொடுக்க வேண்டும் என்கிறாள். ஆனால் கலா ₹59 கொடுக்க வேண்டும் எனக் கூறுகிறாள். இதில் யார் கூறியது சரி?

தீர்வு:

எ.கா. 4: ஒரு நியாய விலைக் கடையில் 5000 குடும்பங்களுக்கு 1,00,000 கிலோ கிராம் அரிசி வழங்கப்படுகிறது எனில் ஒவ்வொரு குடும்பத்திற்கும் வழங்கப்பட்ட அரிசியின் அளவைக் காண்க?

தீர்வு:

எ.கா. 5: (9 × 5) + (10 × 12) ஐ மரவுரு வரைபடமாக மாற்றுக.

தீர்வு:

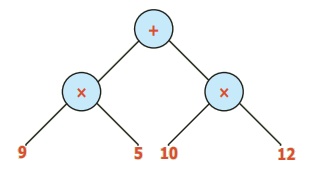
எ.கா. 6: (10 × 9) – [(8 × 2) +3] ஐ மரவுரு வரைபடமாக மாற்றுக.

தீர்வு:

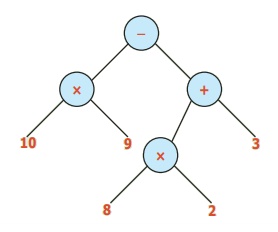
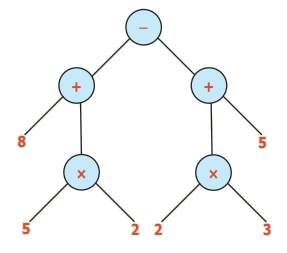
எ.கா. 7: [8+ (5× 2)] – [(2×3) +5] ஐ மரவுரு வரைபடமாக மாற்றுக.

தீர்வு:

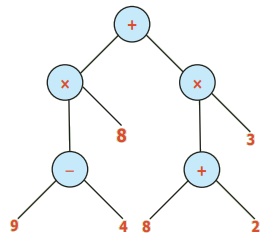
எ.கா. 8: [(9–4)×8] + [(8+2)×3] ஐ மரவுரு வரைபடமாக மாற்றுக.

தீர்வு:

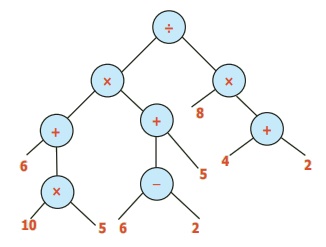
எ.கா. 9: {[(10 × 5) + 6] × [5 + (6 – 2)]} ÷ [8 × (4 + 2) ] ஐ மரவுரு வரைபடமாக மாற்றுக.

தீர்வு:

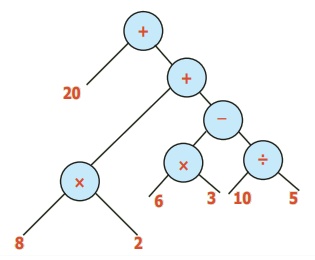
எ.கா. 10: 20 + [8 × 2+{(6 × 3) – (10 ÷  5)}]  ஐ மரவுரு வரைபடமாக மாற்றுக.

தீர்வு: