மாற்றமிலி – எடுத்துக்காட்டுகள்

மாற்றமிலி – எடுத்துக்காட்டுகள்

மடக்கு மாற்றமிலி ஒரு மடக்கின் நான்கு மிக முக்கியமான இடங்களில் மெய்யாக இருக்கும். மடக்கு மாற்றமிலியைப் பயன்படுத்தி, நாம் ஒரு மடக்கை உருவாக்கலாம். மேலும், அந்த இடங்களில் மாறிகளின் சில பண்புகளையும் நாம் நிரூபிக்கலாம். 

எடுத்துக்காட்டு 8.5

an என்பதைக் கணக்கிட ஒரு சுழற்சி நெறிமுறையை வடிவமைக்கவும். அந்த நெறிமுறைக்கு power(a,n) என்று பெயரிடுவோம். எடுத்துக்காட்டாக, 

power(10, 4) = 10000

power (5 , 3) = 125

power (2 , 5) = 32

power (a, n) என்ற நெறிமுறை a- யை ஒட்டுமொத்தமாக 'n' முறை பெருக்கி an ஐ கணக்கிடுகிறது.

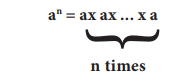
அதன் விவரக்குறிப்பும், மடக்கு மாற்றமிலியும் குறிப்புரைகளாகக் கீழே காட்டப்பட்டுள்ளன. 

power (a, n)

--inputs: n ஒரு நேர்மறை எண்

outputs: p = an

p, i := 1 , 0

while i ≠ n

-- மடக்கு மாற்றமிலி: p = ai

p, i := p × a, i+1 

power(2, 5) எவ்வாறு படிப்படியாகச் செயல்படுத்தப்படுகிறது என்பது அட்டவணை 8.1 இல் காட்டப்பட்டுள்ளது. ஒவ்வொரு வரிசையும் ஒரு சுழற்சியின் முடிவில் p, i என்ற இரண்டு மாறிகளின் மதிப்பையும், அவை எவ்வாறு கணக்கிடப்பட்டன என்றும் காண்பிக்கிறது. p=ai என்பது மடக்கின் தொடக்கத்தில் மெய்யாக உள்ளது என்றும், ஒவ்வொரு வரிசையிலும் அது மெய்யாகவே இருக்கிறது என்றும் காணலாம். ஆகவே, இது ஒரு மடக்கு மாற்றமிலி எனப்படும்.

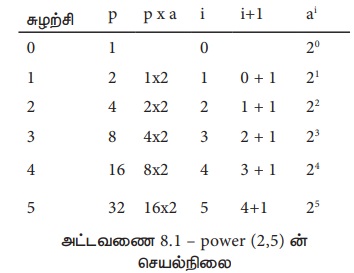
மடக்கு முடியும்போது, p = ai என்பது மெய்யாகவே இருக்கிறது. மேலும், i = 5. எனவே, p = a5 ஆக அமைந்துள்ளது. பொதுவாகச் சொல்வதானால், மடக்கு முடியும்போது p = an எவ்வாறு, power (a, n) விவரக்குறிப்பை நிறைவு செய்கிறது என்று நாம் சரிபார்த்துவிட்டோம். 

எடுத்துக்காட்டு 8.6:

எடுத்துக்காட்டு 6:11யிலுள்ள சாக்லேட் பார் எடுத்துக்காட்டை நினைவு கொள்க. ஒரு முழு சாக்லேட்டைத் தனித்தனிச் சதுரங்களாக உடைப்பதற்கு எத்தனை வெட்டுக்கள் தேவை? எத்தனை துண்டுகள், எத்தனை வெட்டுக்கள் என்பதைக் குறிக்க முறையே p, c என்ற மாறிகளைப் பயன்படுத்தலாம். ஒவ்வொரு முறையும் வெட்டும்போதும், வெட்டுகளின் எண்ணிக்கை ஒன்று கூடுகிறது, துண்டுகளின் எண்ணிக்கைம் ஒன்று கூடுகிறது. இதை ஒரு மதிப்பிருத்தலின் மூலம் குறப்பிடலாம்.

p, c := p + 1, c + 1 

முழு சாக்லேட்டை வெட்டும் செயல்முறையை ஒரு மடக்கைக் கொண்டு விளக்கலாம். தொடங்கும் போது ஒரேவொரு துண்டு உள்ளது, ஒருமுறைகூட வெட்டப்படவில்லை . அதாவது, p = 1, c = 0 மொத்தத் தனித்தனி சதுரங்களின் எண்ணிக்கையை n என்று குறிப்பிடுவோம். துண்டுகளின் எண்ணிக்கை pம், தனித்தனி சதுரங்களின் எண்ணிக்கை nம் சமமாகும் போது மடக்கு முடிவடைகிறது. 

p, c : = 1 , 0 

while p ≠ n 

p, c := p + 1, c+1 

p - c என்பது, p, c := p + 1, c + 1 என்ற மதிப்பிருத்தலின் மாற்றமிலி என்று எடுத்துக்காட்டு 8.2இல் பார்த்தோம். p-c= k என்க. இதில் k ஒரு நிலையான மதிப்பு. நெறிமுறையில் எந்தெந்த இடங்களில் p - c = k என்பது மெய்யாக இருக்கிறது என்று கீழேக் கொடுக்கப்பட்டுள்ள நெறிமுறையிலும், பாய்வுப்படம் 8.2யிலும் காட்டப்படுள்ளது.

p, c : = 1 , 0 

1. -- p - c = k 

while p ≠ n 

2. -- p - c = k 

p, c := p+1, c+1 

3. -- p - c = k 

4. --p-c=k,p=n 

p - c = k என்ற மடக்கு மாற்றமிலி, மடக்கின் தொடக்கத்தில் (முதல் வரி) மெய்யாக இருக்கிறது. மேலும், மடக்கின் தொடக்கத்தில் p - c = 1. எனவே, k = 1 மடக்கு மாற்றமிலிலி p - c = 1 எனக் குறிப்பிடலாம்.

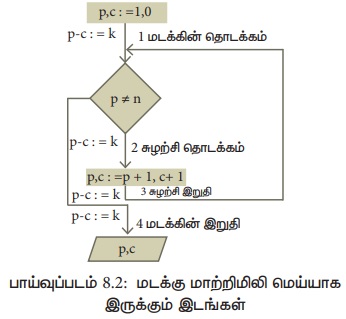
மடக்கு முடியும்போது (நான்காவது வரி), மடக்கு மாற்றிமிலி , p-c = 1, இன்னும் மெய்யாகவே இருக்கிறது. மேலும், மடக்கின் நிபந்தனை p + n என்பது பொய்யாக உள்ளது. எனவே, p - c = 1, p = n இவைகளிலிருந்து 

(1) p - c = 1 என்பது மடக்கு மாற்றமிலி 

(2) p = n என்பது மடக்கின் முடிவு 

(3) n – c = 1 என்பது (1), (2)வது வரிகளிலிருந்து 

(4) c = n - 1 என்பது (3)வது வரியிலிருந்து 

மடக்கு முடியும்போது சதுரங்களின் எண்ணிக்கையைவிட வெட்டுகளின் எண்ணிக்கை ஒன்று குறைவாக இருக்கிறது. 

எடுத்துக்காட்டு 8.7:

6 மரங்கள் சமதூரத்தில் இருக்கின்றன. ஒவ்வொரு மரத்திலும் ஒரு குருவிவீதம் 6 மரங்களில் மொத்தம் 6 குருவிகள் உட்கார்ந்திருக்கின்றன. ஒரு குருவி ஒரு மரத்திலிருந்து இன்னொரு மரத்துக்குப் பறந்து போகும் அதே நேரத்தில் மற்றொரு குருவி முந்தைய குருவி எவ்வளவு தூரம் பறந்துபோனதோ அவ்வளவு தூரம் இன்னொரு மரத்திற்குப் பறந்துபோகிறது. ஆனால், இந்த குருவி முதலாவது குருவிக்கு எதிர்த்திசையில் பறந்து போகிறது. அப்படியானால், எல்லாக் குருவிகளும் ஒரே மரத்தில் உட்காருவது சாத்தியமா? 

மரங்களை 1முதல் 6வரை வரிசைப்படுத்துவோம். குருவிகள் உட்கார்ந்திருக்கின்ற மரங்களின் வரிசை எண், குருவிகளின் வரிசை எண் என்று வைத்துக்கொள்வோம். ஒரு ஜோடிக் குருவிகள் பறந்து போவதை மடக்கின் ஒரு சுழற்சியாக எடுத்துக் கொள்ளலாம். ஒரு குருவி i என்ற மரத்திலிருந்து i + d க்குப் பறந்துபோகும்போது, இன்னொரு குருவி j என்ற மரத்திலிருந்து j-dக்குப் பறந்து போகிறது. இவ்வாறு, ஒவ்வொரு சுழற்சிக்கு வரிசை எண்களின் பின்பும், குருவிகளின் வரிசை எண்களின் மொத்த எண்ணிக்கை S என்பது மாறாமல் அப்படியே இருக்கிறது. மேலும், ஒரு மடக்கு மாற்றமிலி மடக்கின் தொடக்கத்திலும், முடிவிலும் மெய்யாகவே உள்ளது. 

மடக்கின் தொடக்கத்தில் மதிப்பு

S = 1 + 2 + 3 + 4 + 5 + 6 = 21 

மடக்கு முடியும்போதும், மடக்கு மாற்றமிலியின் மதிப்பு மாறாமல் அப்படியே இருக்கிறது. எனினும், மடக்கு முடியும்போது, எல்லாக் குருவிகளும் k என்ற ஒரே மரத்தில் இருப்பதாக வைத்துக்கொள்வோம். அப்படியானால் S = 6k

S = 21, மடக்கின் தொடக்கத்தில் மடக்கு மாற்றமிலி

S = 6k, மடக்கின் முடிவில் மடக்கு மாற்றமிலி 

6k = 21, தொடக்கத்திலும், முடிவிலும் மடக்கு மாற்றமிலிக்கு ஒரே மதிப்பு இருக்கிறது 

21, 6 என் பெருக்கம் 

இது சாத்தியம் இல்லை. 21, 6ன் பெருக்கம் இல்லை. குருவிகளின் வரிசை எண்களின் கடைசி மதிப்பு மடக்கு மாற்றமிலியில் சாத்தியமில்லை . ஆகையால், எல்லாக் குருவிகளும் ஒரே மரத்தில் வந்து சேருவது சாத்தியமில்லை. 

எடுத்துக்காட்டு 8.8.

எடுத்துக்காட்டு 6.3இல் கொடுக்கப்பட்ட குரோம்லேண்டில் பச்சோந்திகள் என்ற சிக்கலை எடுத்துக் கொள்வோம். அவைகளில் 13 சிவப்பு, 15 பச்சை மற்றும் 17 நீல நீர பச்சோந்திகள் உள்ளன. இவற்றில் வேறுபட்ட நிறங்களையுடைய இரண்டு பச்சோந்திகள் சந்திக்கும்போது, அவையிரண்டும் தங்கள் நிறத்தை மூன்றாவது நிறமாக மாற்றிக் கொள்ளுகின்றன (எடுத்துக்காட்டாக, சிவப்பு நிற பச்சோந்தியும், பச்சை நிற பச்சோந்தியும் சந்தித்தால், அவையிரண்டும் நீலநிற பச்சோந்தியாக மாறிவிடுகின்றன). எல்லாப் பச்சோந்திகளும் நீல நிறமாக மாறிவிடுமாறு அவைகள் சந்திக்க ஏற்பாடு செய்வது சாத்தியமா?

r, g மற்றும் என்பது முறையே சிவப்பு, பச்சை, நீலநிற பச்சோந்திகளின் எண்ணிக்கை என்று வைத்துக்கொள்வோம். வேறு நிறங்களுடைய இரண்டு பச்சோந்திகளின் சந்திப்பைச் சுழற்ச்சி முறையில் குறிக்கலாம். ஒரு சந்திப்பு r, g, b யை (r - 1, g - 1, b + 2) அல்லது (r - 1, g + 2, b - 1) அல்லது (r + 2, g - 1, b - 1) என்று மாற்றுகிறது. எடுத்துக்காட்டாக, ஒரு சிவப்பு நிற பச்சோந்தியும், ஒரு பச்சைநிற பச்சோந்தியும் சந்திக்கின்றன என்று வைத்துக்கொள்வோம். அப்போது,

r,g, b := r - 1, g - 1, b + 2

எந்த இரண்டு விதமான பச்சோந்திகளின் எண்ணிக்கையின் வேறுபாடும் மாறாது அல்லது மாறினாலும், 3 என்ற எண்ணிக்கையில் மாறும். இது ஒரு மாற்றமிலி.

r - 1 - (g - 1) = r - g 

r - 1 - (b + 2) = (r - b) - 3 

g - 1 - (b + 2) = (g - b) – 3 

எல்லா மூன்று வகைகளைப் பொறுத்தவரையிலும் இது மெய்யாக உள்ளது. சுழற்சியின் தொடக்கத்தில், ஏதேனும் இரண்டு வகை பச்சோந்திகளின் எண்ணிக்கையிலுள்ள வேறுபாடு 3ன் மடங்காக இருந்தால், அதனை மூன்று மூன்றாக குறைத்து சுழற்ச்சியின் இறுதியில் 0 என மாற்றலாம். 

எனினும், 

எந்த இரண்டு நிறங்களின் எண்ணிக்கைகளின் வேறுபாடும், 3ன் மடங்காக இல்லை. ஆகையால், எல்லாப்

r - g = 13 - 15 = -2

g - b = 15 - 17 = -2

g - r = 17 - 13 =4 

பச்சோந்திகளையும் ஒரே நிறத்திற்கு மாற்ற முடியாது. 

எடுத்துக்காட்டு 8.9. பந்துகளின் குடுவை : வெள்ளை மற்றும் கருப்பு நிறமுள்ள இரண்டு விதமான பந்துகள் நிரம்பிய ஒரு குடுவை கொடுக்கப்பட்டுள்ளது. அதிலிருந்து ஏதேனும் இரண்டு பந்துகளை எடுக்க வேண்டும். எடுக்கப்பட்ட இரண்டு பந்துகளும் வெள்ளை நிறமாயின், அவற்றை வெளியே எறிந்து விட்டு, ஒரு புதிய கருப்பு நிற பந்தை குடுவையின் உள்ள போட வேண்டும். (தேவையான அளவுக்குப் பந்துகள் கிடைக்கும் என்று வைத்துக்கொள்வோம்). இரண்டும் வெவ்வேறு நிறமென்றால், வெள்ளை நிறத்தைக் குடுவைக்குள் போட்டுவிட்டு, கருப்பு நிறத்தை எறிந்துவிடு. முதலில் எத்தனை வெள்ளை நிறப் பந்துகளும், கருப்பு நிறப் பந்துகளும் இருந்தன என்று உனக்குத் தெரிந்தால், குடுவையில் இருக்கும் கடைசிப் பந்தின் நிறம் என்ன?

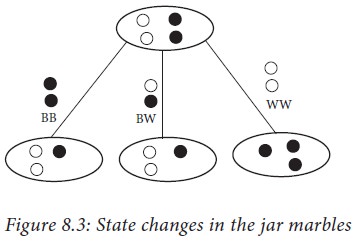
w, b என்ற இரண்டு மாறிகள் குடுவையிலுள்ள வெள்ளை மற்றும் கருப்புநிறப் பந்துகளின் எண்ணிக்கையைக் குறிக்கின்றன. ஒவ்வொரு சுழற்ச்சியிலும், குடுவையிலிருந்து வெளியே எடுக்கும் இரண்டு பந்துகளின் நிறத்தைப் பொறுத்து கருப்பு கருப்பு, கருப்பு வெள்ளை, வெள்ளை வெள்ளை என்று மாறுகின்றன: இது படம் 8.3 இல் கொடுக்கப்பட்டுள்ளது. கீழே கொடுக்கப்பட்டுள்ள நெறிமுறையில் இது விளக்கப்பட்டுள்ளது. 

1 குடுவையில் குறைந்தது இரண்டு பந்துகள் இருந்தால்

2 -- b, w 

3 ஏதாவது இரண்டு பந்துகளை எடுக்கவும்

4 Case இரண்டும் கருப்பாக இருந்தால் -- BB

5 இரண்டு பந்துகளையும் எறிந்துவிடு 

6 ஒரு கருப்பு பந்தை குடுவையில் போடு 

7 - - b = b' - 1, w = w', b + w = b' + w' - 1

8 Case இரண்டும் வெள்ளையாக இருந்தால் --WW

9 இரண்டு பந்துகளையும் எறிந்துவிடு 

10 ஒரு கருப்பு பந்தை குடுவையில் போடு 

11 - - b = b' + 1, w = w' - 2, b + w = b' + w' - 1 

12 else - - b w 

13 கருப்பு நிற பந்தை எறிந்துவிடு 

14 வெள்ளை நிற பந்தை குடுவையில் போடு 

15 - - b = b' - 1, w = w', b + w = b' + w' - 1

ஒவ்வொரு நிலையிலும் b, w, b + w எப்படி மாறுகின்றன என்று நெறிமுறையில் காட்டப்பட்டுள்ளது. b', w' ஆகியவை இரண்டு பந்துகளை எடுப்பதற்கு முன் மாறிகளின் மதிப்பாகும். w எப்படி மாறுகிறது என்று கவனிக்கவும். ஒன்று, அது மாறுவதில்லை அல்லது 2 குறைகிறது. தொடக்கத்தில் w ஒற்றை படையாக இருப்பின், கடைசி வரை ஒற்றைப் படையாகவே இருக்கும். இரட்டைப் படையாக இருப்பினும், கடைசி வரை இரட்டைப் படையாகவே இருக்கும். எனவே, சமநிலை மாறாது என்பதே இதன் பொருள் w யின் சமநிலை மாற்றமிலி.

தொடக்கத்தில் w இரட்டைப்படை என்று வைத்துக்கொள்வோம். முடிவிலும் w இரட்டைப்படையாகவே இருக்கும். மேலும், இப்போது ஒரேவொரு பந்துதான் மீதியிருக்கிறது. w + b = 1 

1 w + b = 1 மடக்கின் இறுதி 

2 w = 0 அல்ல து w = 1 1 லிருந்து வரியிலிருந்து 

3 w இரட்டைப்படை மடக்கு மாற்றமிலி 

4 w = 2,3 லிருந்து 

5 b = 1,4 லிருந்து 

கடைசிப் பந்து கருப்பாகத்தான் இருக்க வேண்டும். அதுபோல, தொடக்கத்தில் வெள்ளைப் பந்துகள் ஒற்றைப்படையாக இருந்தால், கடைசிப் பந்து வெள்ளையாக இருக்க வேண்டும்.

கேள்வி : கடைசியில் ஒரேவொரு பந்துதான் இருக்கிறது என்ற நிலையை நாம் எப்போதாவது அடைவோமா? ஆம், ஏனென்றால், ஒவ்வொரு படியிலும், b + w பந்துகளின் மொத்த எண்ணிக்கை ஒன்று குறைந்து கொண்டே போகும். எனவே, படிப்படியாகக் குறைந்து, கடைசியில் அது 1 என்றாகிவிடும்.