கணினி அறிவியல் - தற்சுழற்சி | 11th Computer Science : Chapter 8 : Iteration and recursion
11வது கணினி அறிவியல் : அலகு 8 : சுழற்சியும், தற்சுழற்சியும்
தற்சுழற்சி
தற்சுழற்சி (Recursion)
தற்சுழற்சி என்பது ஒரு நெறிமுறை வடிவமைப்பு நுட்பமாகும். இது கணிதத்தூண்டலோடு நெருங்கிய தொடர்புடையது. இது சுழற்சிக்கு இணையானது. ஆனால் அதைவிட அதிகப் பயனுள்ளது. தற்சுழற்சியைப் பயன்படுத்தி, கொடுக்கப்பட்ட உள்ளீட்டின் பகுதிகளைக் கொண்டு ஒரு சிக்கலின் சான்றுருக்களை தீர்ப்பதின் மூலம், சிக்கலைக் கொடுக்கப்பட்ட உள்ளீட்டிற்காகத் தீர்க்க முடியும்.
எடுத்துக்காட்டு 8.10.
வாடிக்கையாளர்கள் ஒரு சேவைக்காக வரிசையில் காத்துக்கொண்டிருக்கிறார்கள். சேவை செய்பவர் வரிசையில் எத்தனை பேர் காத்திருக்கிறார்கள் என்று தெரிந்துக்கொள்ள விரும்புகிறார்.
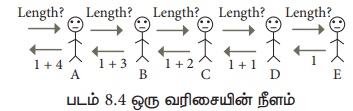
அவர் வரிசையின் நீளத்தைத் தானாகவே கணக்கிடுவதற்குப் பதிலாக, வரிசையில் முதலாவதாக நிற்கின்ற வாடிக்கையாளர் Aயிடம், வரிசையின் நீளம் என்ன? என்று கேட்கிறார். வாடிக்கையாளர் A, வாடிக்கையாளர் B யிடம், நீளம் என்ன? என்று கேட்கிறார். வாடிக்கையாளார் B வாடிக்கையாளர் C யிடம் கேட்கிறார். இப்படி ஒவ்வொருவரும் தனக்குப்பின் இருப்பவரிடம் கேட்கிறார்கள் வரிசையின் கடைசியில் இருக்கும் வாடிக்கையாளர் E என்று வைத்துக்கொள்வோம். அவரிடம் இந்த கேள்வியைக் கேட்கும் போது, அவர் தன்னிடம் கேட்ட D யிடம் "1” என்று பதிலளிக்கிறார். D,"1+1=2” என்று Cக்குப் பதிலளிக்கிறார். C,"1+2=3" என்று நக்குப் பதிலளிக்கிறார். B,"1+3=4” என்று A க்குப் பதிலளிக்கிறார். A,"1+4=5'' என்று தன்னிடம் கேட்ட சேவையாளருக்குப் பதிலளிக்கிறார்.
1. தற்சுழற்ச்சி முறை
எடுத்துக்காட்டு 8.10
தற்சுழற்சி முறையை விளக்குகிறது. A, B, C, D, E என்ற வாடிக்கையாளர்களாலான வரிசையை [A, B, C, D, E] என்று குறிப்பிடுவோம். இப்போது [A, B, C, D, E] என்ற வரிசைமுறையின் நீளத்தைக் கணக்கிட வேண்டும். சிக்கலை தீர்க்கின்ற தீர்ப்பானுக்கு (solver), length என்று பெயரிடுவோம். இந்த length என்ற தீர்ப்பானுக்கு நாம் ஒரு வரிசையை உள்ளீடாகத் தந்தால், அது அந்த வரிசைமுறையின் நீளத்தை வெளியீடாகக் கொடுக்கும்.
length [A, B, C, D, E] = 5
length என்ற தீர்ப்பான் [A, B, C, D, E] என்ற வரிசையை அதன் முதல் வாடிக்கையாளர் என்றும், எஞ்சியுள்ள வரிசை என்றும், இரண்டு பகுதிகளாகப் பிரிக்கின்றது.
முதல் (first) [A, B, C, D, E] = A
எஞ்சியுள்ளது (rest) [A, B, C, D, E] = [B, C, D, E]
ஒரு சிக்கலைத் தற்சுழற்சி முறையில் தீர்ப்பதற்கு, length என்ற தீர்ப்பான் [B, C, D, E] என்ற அளவு குறைக்கப்பட்ட வரிசையை வேறொரு துணைத்தீர்ப்பானுக்கு (Sub solver) உள்ளீடாகக் கடத்துகிறது. இந்த துணைத்தீர்ப்பான் length என்ற தீர்ப்பானின் மற்றொரு சான்றுரு. இந்த துணைத்தீர்ப்பான் (B, C, D, E] என்ற வரிசையின் நீளத்தை வெளியீடாகத் தருவதாகக் கருதிக் கொண்டு, அதனுடன் 1 ஐக் கூட்டி, அதை [A, B, C, D, E] யின் நீளம் என்று வெளியீடாகத் தருகிறது.
length [A, B, C, D, E] = 1 + length [B, C, D, E]
இப்படி ஒவ்வொரு தீர்ப்பானும்
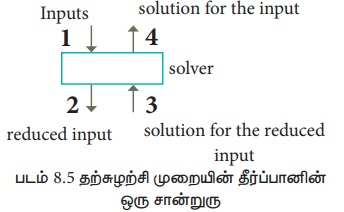
1. ஓர் உள்ளீட்டைப் பெறுகிறது
2. அளவு குறைக்கப்பட்ட ஓர் உள்ளீட்டைத் துணைத்தீர்ப்பானுக்குக் கடத்துகிறது.
3. அளவு குறைக்கப்பட்ட உள்ளீட்டிற்கானத் தீர்வை துணைத்தீர்ப்பானிடமிருந்து பெறுகிறது.
4. கொடுக்கப்பட்ட உள்ளீட்டிற்கான தீர்வை உருவாக்குகிறது.
எடுத்துக்காட்டு 8.10 இல் ஒவ்வொரு தீர்ப்பானும் பெற்றுக்கொள்ளும் உள்ளீட்டையும், உருவாக்கும் தீர்வையும், படம் 8.6 காண்பிக்கிறது. ஒவ்வொரு தீர்ப்பானும் தான் பெறும் உள்ளீட்டின் அளவில் 1யைக் குறைத்து, அதை ஒரு துணைத்தீர்ப்பானுக்குக் கடத்துகிறது. இவ்வாறு, 5 தீர்ப்பான்கள் தேவைப்படுகிறது. ஒரு தீர்ப்பான் பெறுகிற உள்ளீடு ஒரு தீர்வை நேரடியாக வெளியீடு செய்யும் அளவுக்கு மிகச் சிறியதாகும் வரை இப்படிக் கடத்துதல் தொடர்கிறது. கடைசித் தீர்ப்பான் (E)ஐ உள்ளீடாகப் பெறுகிறது. (E) போதுமான அளவுக்குச் சிறியதாக இருப்பதால், அதைப் பெறும் தீர்ப்பான் (E)யின் நீளம் 1 என்று உடனடியாக வெளியிடுகிறது. அத்துடன் அதன் தற்சுழற்ச்சி நின்றுவிடுகிறது.
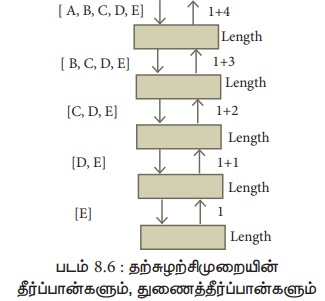
[A, B, C, D, E] என்ற நீளத்திற்கான தற்சுழற்சிமுறைபடம் 8.7இல் காட்டப்பட்டுள்ளது.
1. length [A,B,C,D,E]
2 = 1 + length [B,C,D,E]
3 = 1 +1 + length [C,D,E]
4 = 1 + 1+ 1 + length [D,E]
5 = 1 +1+ 1 + 1 + length [E]
6 = 1 + 1 + 1 + 1 +1
7 = 1 +1 +1 + 2
8 = 1 + 1 + 3
9 = 1 + 4 21 13
10 = 5

2. தற்சுழற்சி முறையில் சிக்கலைத் தீர்த்தல்
ஒவ்வொரு தீர்ப்பானும் தான் பெறும் உள்ளீட்டின் அளவை சோதித்தறிய வேண்டும் அந்த உள்ளீட்டின் அளவு போதுமான அளவுக்குச் சிறியதாக இருந்தால், தீர்ப்பான் சிக்கலுக்கான தீர்வை நேரடியாக வெளியிட வேண்டும். உள்ளீட்டின் அளவு போதுமான அளவுக்குச் சிறியதாக இல்லையென்றால், தீர்ப்பான் உள்ளீட்டின் அளவைக் குறைத்து, குறைக்கப்பட்ட உள்ளீட்டை வைத்து சிக்கலைத் தீர்க்குமாறு ஒரு துணைத்தீர்ப்பானை அழைக்க வேண்டும். எடுத்துக்காட்டு 8.10க்கான தீர்ப்பானின் நெறிமுறையைப் பின்வருமாறு சொல்லலாம்.

தற்சுழற்சி முறையில் ஒரு சிக்கலைத் தீர்ப்பதற்கு, தீர்ப்பான் சிக்கலை துணைச் சிக்கல்களாகப் பிரித்து, ஒவ்வொரு துணைச்சிக்கலைத் தீர்ப்பதற்கும், ஒரு துணைத்தீர்ப்பானை அழைக்க வேண்டும். ஒவ்வொரு துணைத் தீர்ப்பானும் தீர்ப்பானுடைய இன்னொரு சான்றுருவேயாகும். துணைச்சிக்கலுக்காக இடப்படும் உள்ளீட்டின் அளவு மூலச் சிக்கலுக்கான உள்ளீட்டின் அளவைவிடச் சிறியதாக இருக்க வேண்டும். ஒரு தீர்ப்பான் இன்னொரு துணைத்தீர்ப்பானை அழைக்கும்போது, அது தற்சுழற்சி அழைப்பு என்று வழங்கப்படுகிறது.
தற்சுழற்சியாக அழைக்கப்படும் துணைத்தீர்ப்பான் தான் பெறும் துணைச்சிக்கலுக்கான தீர்வை வெளியிடுகிறது என்று தீர்ப்பான் அனுமானிப்பதற்கு தற்சுழற்சி அனுமதிக்கிறது. அதன்பின் துணைச்சிக்கலின் தீர்விலிருந்து, கொடுக்கப்பட்ட சிக்கலுக்கான தீர்வை தீர்ப்பான் அமைக்கிறது.
துணைத்தீர்ப்பான்கள் சிக்கல்களை மேலும் சிறிய அளவிலான துணைச்சிக்கல்களாகக் குறைத்துக் கொண்டே போகும்போது, இறுதியாக, தற்சுழற்சியின் தேவையில்லாமல் நேரடியாகவே தீர்த்துக்கொள்ளும் அளவுக்குச் துணைச்சிக்கல்கள் மிகச் சிறியவைகளாகிவிடுகின்றன. ஆகையால், ஒரு தற்சுழற்சித் தீர்ப்பானுக்கு இரண்டு (cases) நிலைகள் உள்ளன:
1. அடிப்படை நிலை (Base Case): நேரடியாகத் தீர்க்கும் அளவுக்குச் சிக்கலின் அளவு சிறியதாக இருக்கிறது. அப்பொழுது தீர்வை உடனடியாக வெளியீடு செய்யலாம். குறைந்தது ஓர் அடிப்படை நிலைமையாவது இருக்க வேண்டும்.
2. தற்சுழற்சிப் படிநிலை (Recursion step) : சிக்கலின் அளவு அந்த அளவுக்குச் சிறியதல்ல என்பது வரை, சிக்கலைத் துணைச் சிக்கல்களாகப் பகுக்க வேண்டும். அந்த துணைச்சிக்கல்கள் கொடுக்கப்பட்ட சிக்கலின் அளவைவிட கண்டிப்பாகச் சிறியதாக இருக்க வேண்டும். பின்பு, துணைச்சிக்கலைத் தீர்க்க ஒரு துணைத்தீர்ப்பானை அழைக்க வேண்டும். அந்த துணைத்தீர்ப்பான் துணைச்சிக்கலுக்கான தீர்வை வெளியிடுவதாகக் கருதி, கொடுக்கப்பட்ட சிக்கலுக்கானத் தீர்வை அமைக்க வேண்டும்.
தற்சுழற்சி முறையைப் பயன்படுத்திச்சிக்கலைத் தீர்க்கும் நுட்பத்தைப் பின்வரும் நெறிமுறை காண்பிக்கிறது.
solver (input)
if உள்ளீடு போதுமான அளவுக்கு சிறியதாக இருக்குமெனில்,
தீர்வை கட்டமைக்கவும்
else
சிறிதாக்கப்பட்ட உள்ளீட்டுக்கான துணைச் சிக்கல்களைக் கண்டுப்பிடிக்கவும்.
துணை சிக்கலின் தீர்வு = ஒவ்வொரு துணை சிக்கலின் தீர்ப்பான்.
துணைச் சிக்கல்களிலிருந்து, மூலச் சிக்கலுக்கான தீர்வைக் கட்டமைத்தல்.
தற்சுழற்சியைப் பயன்படுத்தி ஒரு சிக்கலைத் தீர்க்கும்போதெல்லாம், இந்த இரண்டு நிலைமைகளை நாம் உறுதி செய்ய வேண்டும் :
(1) தற்சுழற்சிப் படியில், தற்சுழற்சி அழைப்புக்கான உள்ளீட்டின் அளவு கொடுக்கப்பட்ட உள்ளீட்டின் அளவைவிட கண்டிப்பாகச் சிறியதாக இருக்க வேண்டும்.
(2) குறைந்தது, ஓர் அடிப்படை நிலைமையாவது இருக்க வேண்டும்.
3. தற்சுழற்சி - எடுத்துக்காட்டுகள்
எடுத்துக்காட்டு 8.11.
ஒரு வரிசைமுறையின் நீளத்தைக் கணக்கிடுவதற்கு, தற்சுழற்சி நெறிமுறையைப் பின்வருமாறு எழுதலாம். நீளம் (s)
length (s)
-- inputs : S
-- outputs : Sன் நீளம்
if sல் ஒரு வாடிக்கையாளர் உள்ளார் எனில் –
- அடிப்படை நிலை
1
else
1 + length (tail (s)) - - தற்சுழற்சி படிநிலை
எடுத்துக்காட்டு 8.12.
an யைக் கணக்கிட ஒரு தற்சுழற்சி நெறிமுறையை வடிவமைக்கவும்.
எடுத்துக்காட்டு 8.5ல், an யைக் கணக்கிட நாம் ஒரு சுழற்சி நெறிமுறையை அமைத்தோம். an ஐ தற்சுழற்சி முறையில் இவ்வாறு வரையறுக்கலாம்.

இந்த தற்சுழற்சி வரையறையை, power (a, n) யைக் கணக்கிடுவதற்கான தற்சுழற்சி தீர்ப்பாகப் பின்வருமாறு எழுதலாம். power (a, n)
power (a, n)
-- inputs : n is an integer, n ≥ 0
-- outputs : an
if n = 0 -- base case
1
else -- recursion step
a x power (a, n-1)
power (a, n) ஐக் கணக்கிடுவதற்கான தற்சுழற்சி முறையும், அதன் தீர்ப்பான்களும் படம் 8.8 இல் காட்டப்பட்டுள்ளன.
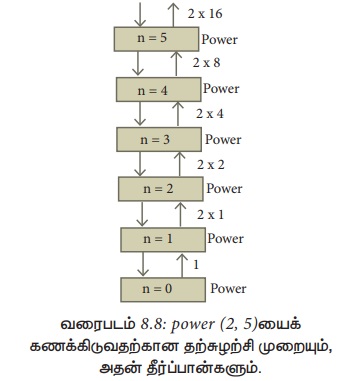
power (2, 5) யிலிருந்து வரக்கூடிய தற்சுழற்சி முறை வரைபடம் 8.9-ல் காட்டப்பட்டுள்ளது.

power (2,5)
= 2 × power (2,4)
= 2 × 2 × power(2,3)
= 2 × 2 × 2 × power(2, 2)
= 2 × 2 × 2 × 2 × power (2,1)
= 2 × 2 × 2 × 2 × 2 × power (2,0)
= 2 × 2 × 2 × 2 × 2 × 1
= 2 × 2 × 2 × 2 × 2
= 2 × 2 × 2 × 4
= 2 × 2 × 8
= 2 × 16
= 32
வரைபடம் 8.9 power (2, 5)க்கான தற்சுழற்சி முறை
எடுத்துக்காட்டு 8.13.
மூலை மூடப்பட்ட பலகை என்பது 2n × 2n சதுரங்களாலானது. அதில் ஒரு மூலைச் சதுரம் ஒரு தனிச் சதுர ஓட்டினால் மூடப்பட்டிருக்கிறது. அடுத்தடுத்த மூன்று சதுரங்களைக் கொண்டு L வடிவத்தில் அமைக்கப்பட்ட ஓட்டுக்கு முக்கோண ஓடு என்று பெயர் (படம் 8.10ஐப் பார்க்கவும்) மூலை மூடப்பட்ட ஒரு பலகையை இந்த L வடிவ ஓடுகளைக்கொண்டு, ஒன்றின் மேல் ஒன்று வராதபடிக்கு, மூடவும். L வடிவ ஓடுகளைத் தேவைக்கேற்றாற்போல் சுழற்றிக்கொள்ளலாம்.
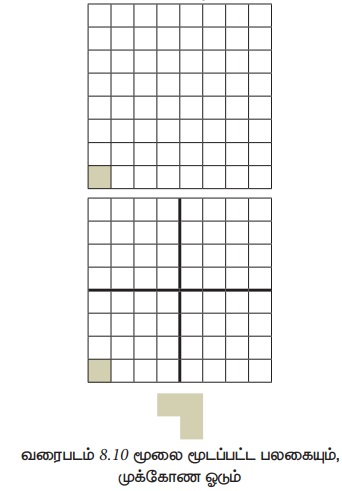
சிக்கலின் அளவு n (2n × 2n) என்ற அளவிலான பலகை. தற்சுழற்சியைப் பயன்படுத்தி நாம் இந்த சிக்கலைத் தீர்க்கலாம். n = 1 என்பது அடிப்படை நிலைமை. இது 2 × 2 அளவிலான மூலை மூடப்பட்ட பலகை. நாம் இதை ஒரு முக்கோண ஓட்டைக் கொண்டு மூடி, சிக்கலைத் தீர்க்கலாம். தற்சுழற்சிப் படியில், 2n × 2n என்ற அளவிலான மூலை மூடப்பட்ட பலகையின் நடுவில் குறுக்காகவும் நெடுக்காகவும் கோடுகளை வரைந்து, அந்தப் பலகையை 4 துணைப்பலகைகளாகப் பிரிக்க வேண்டும். ஒவ்வொரு துணைப்பலகையின் அளவு 2n-1 × 2n-1. வரைபடம் 8.11இல் இடது பக்கப்பலகையில் காட்டப்பட்டுள்ளபடி மூலை மூடப்பட்ட துணைப்பலகையை மூடாதவாறு, ஒரு முக்கோண ஓட்டை முழுப் பலகையின் நடுவில் வைக்கவும். இப்போது ஒவ்வொரு துணைப்பலகையும் 2n-1 × 2n-1 என்ற அளவுகொண்ட மூலை மூடப்பட்ட நான்கு பலகைகளாக உள்ளன.
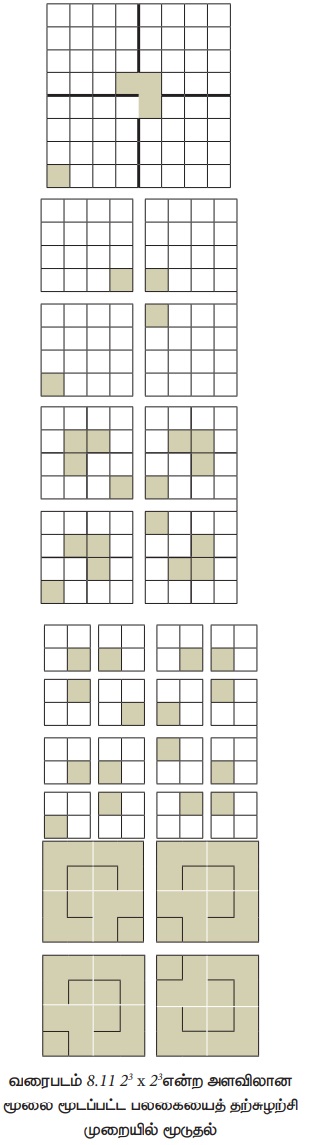
இப்போது கொடுக்கப்பட்ட சிக்கலின் அளவைவிடச் சிறிய அளவிலான 4 துணைச்சிக்கல்களையும் உள்ளன. ஒவ்வொரு துணைச்சிக்கலையும் தற்சுழற்சி முறையில் நாம் தீர்க்கலாம்.
tile corner_covered board of size n
if n = 1 -- base case
cover the 3 squares with one triominoe
else -- recursion step
divide board into 4 sub_boards of size
n - 1
place a triominoe at centre of board,
leaving out the corner_covered sub
-board
tile each sub_board of size n - 1
23 x 23 என்ற அளவிலாலான மூலை மூடப்பட்ட பலகையைத் தற்சுழற்சி முறையில் மூடுவதின் விளைவு படம் -8.11ல் விளக்கப்பட்டுள்ளது.