Я«єЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕ Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї | Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ - Я«єЯ«»Я«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«цЯ«▓Я»Ї (Devising a Coordinate System) | 9th Maths : UNIT 5 : Coordinate Geometry
9 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 5 : Я«єЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕ Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї
Я«єЯ«»Я«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«цЯ«▓Я»Ї (Devising a Coordinate System)
Я«єЯ«»Я«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«цЯ«▓Я»Ї (Devising
a Coordinate System)
Я«еЯ»ђ Я«ЅЯ«ЕЯ»Ї Я«еЯ«БЯ»ЇЯ«фЯ«ЕЯ«┐Я«ЪЯ««Я»Ї 5 Я«џЯ»є.Я««Я»ђ ├Ќ 3 Я«џЯ»є.Я««Я»ђ Я«ЁЯ«│Я«хЯ»ЂЯ«│Я»ЇЯ«│ Я«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ»ѕ Я«хЯ»єЯ«▒Я»ЇЯ«▒Я»ЂЯ«цЯ»Ї Я«цЯ«ЙЯ«│Я«┐Я«▓Я»Ї Я«хЯ«░Я»ѕЯ«»Я«џЯ»Ї Я«џЯ»іЯ«▓Я»ЇЯ«▓Я«хЯ»ЂЯ««Я»Ї. Я«ЁЯ«еЯ»ЇЯ«ц Я«ЁЯ«│Я«хЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«хЯ«ЕЯ«ЙЯ«▓Я»Ї Я«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ««Я»Ї Я«хЯ«░Я»ѕЯ«» Я««Я»ЂЯ«ЪЯ«┐Я«»Я»ЂЯ««Я»Ї, Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Я«јЯ«ЎЯ»ЇЯ«ЋЯ»Є Я«хЯ«░Я»ѕЯ«» Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«јЯ«Е Я«ЁЯ«хЯ«ЕЯ»Ї Я«ЋЯ»ЄЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї, Я«еЯ»ђ Я«јЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐Я«фЯ»Ї Я«фЯ«цЯ«┐Я«▓Я»Ї Я«џЯ»іЯ«▓Я»ЇЯ«хЯ«ЙЯ«»Я»Ї? Я«ЄЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«ЙЯ«░Я»Ї. Я«еЯ»ђ Я«ЄЯ«цЯ»ѕ Я««Я«▒Я»ЇЯ«▒Я»іЯ«░Я»ЂЯ«хЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«јЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐ Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«ЙЯ«»Я»Ї?

Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ»ѓЯ«▒Я«┐Я«» Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ»ѕ (Я«фЯ«ЪЯ««Я»Ї 5.3) Я«єЯ«»Я»ЇЯ«хЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«хЯ»ІЯ««Я»Ї. Я«ЄЯ«цЯ«┐Я«▓Я»Ї Я«џЯ«ЙЯ«цЯ«ЙЯ«░Я«БЯ««Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«хЯ»ђЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«ЁЯ«ЪЯ»ѕЯ«»Я«ЙЯ«│Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ«▓Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я«┐Я«ЋЯ«ЋЯ»Ї Я«ЋЯ«ЪЯ«┐Я«ЕЯ««Я«ЙЯ«Е Я«фЯ«БЯ«┐Я«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«ЊЯ«░Я»Ї Я«ЄЯ«ЪЯ«цЯ»ЇЯ«цЯ»ѕЯ«»Я»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«њЯ«░Я»Ђ Я«фЯ»іЯ«░Я»ЂЯ«│Я»ѕЯ«»Я»І Я«ЁЯ«ЪЯ»ѕЯ«»Я«ЙЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ«ЙЯ«Ћ Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ««Я»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ІЯ«░Я»Ї Я«ЄЯ«ЪЯ«цЯ»ЇЯ«цЯ»ѕЯ«»Я»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«фЯ»іЯ«░Я»ЂЯ«│Я»ѕЯ«»Я»І Я«ЁЯ«ЪЯ»ѕЯ«»Я«ЙЯ«│Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ«▓Я»Ї Я«јЯ«│Я«┐Я«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, Я«њЯ«░Я»Ђ Я«ЋЯ»іЯ«ЪЯ«┐Я«»Я»ѕЯ«фЯ»Ї Я«фЯ»іЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЁЯ«еЯ»ЇЯ«цЯ«ЋЯ»Ї Я«ЋЯ»іЯ«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ«цЯ»Ђ Я«фЯ»ЂЯ«▒Я««Я«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│ Я«хЯ»ђЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«»Я»І, Я«ЁЯ«хЯ»ЇЯ«хЯ»ђЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ђЯ«┤Я»Є Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«ЅЯ«БЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«»Я»І, Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«хЯ«▓Я«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ«▓Я»ѕ Я«ЈЯ«▒Я»ЇЯ«фЯ«┐Я«»Я»ѕЯ«фЯ»Ї (Antenna) Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«»Я»І Я«фЯ»ЄЯ«џЯ«▓Я«ЙЯ««Я»Ї.
Я«фЯ«ЪЯ««Я»Ї 5.4 Я«ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ Я«фЯ»ІЯ«▓Я»Ї, Я«ЄЯ«░Я»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«░Я»ЂЯ«ЋЯ«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«хЯ«░Я»ѕЯ«Ћ. Я«ЄЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«еЯ»ђ Я«ЅЯ«ЕЯ»Ї Я«еЯ«БЯ»ЇЯ«фЯ«ЕЯ«┐Я«ЪЯ««Я»Ї Я«ЋЯ»іЯ«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ««Я»ЇЯ«фЯ«цЯ»ЇЯ«цЯ»ѕ Я«єЯ«░Я««Я»ЇЯ«ф Я«ЄЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»іЯ«цЯ»ЇЯ«ц Я«еЯ»ђЯ«│ Я«ЁЯ«ЋЯ«▓Я«цЯ»ЇЯ«цЯ»ѕ 2 Я«џЯ»є.Я««Я»ђ. Я«хЯ«▓Я«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї, 3 Я«џЯ»є.Я««Я»ђ. Я««Я»ЄЯ«▒Я»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї, Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, Я«ЅЯ«ЕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ«┐Я«џЯ»ѕ Я«цЯ»єЯ«░Я«┐Я«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї 2
Я«џЯ»є.Я««Я»ђ. Я«ЋЯ«┐Я«┤Я«ЋЯ»ЇЯ«ЋЯ»Є , 3 Я«џЯ»є.Я««Я»ђ. Я«хЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ»Є Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ»ѓЯ«▒Я«▓Я«ЙЯ««Я»Ї.
Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Ћ Я«ЄЯ«цЯ»Ђ Я«фЯ»ІЯ«▓Я«хЯ»Є Я«јЯ«БЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«хЯ«▓Я«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я«ЙЯ«Ћ Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї, Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«еЯ«ЙЯ««Я»Ї Я«ЄЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ІЯ«░Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«еЯ«ЋЯ«▓Я»ѕЯ«џЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЂЯ«хЯ»ІЯ««Я»Ї. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▓Я»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»ђЯ«┤Я»ЇЯ«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї Я«ЋЯ»ЂЯ«▒Я»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї. (Я«фЯ«ЪЯ««Я»Ї 5.5).
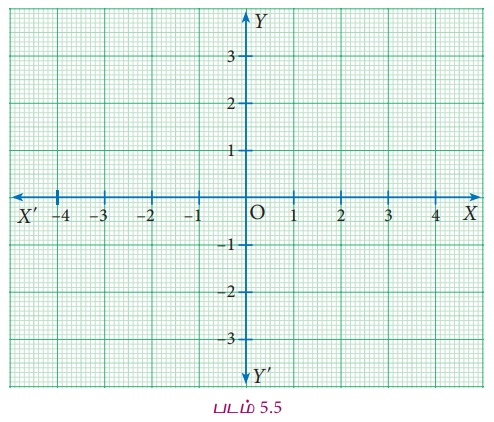
Я«ЄЯ«░Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«јЯ«ЎЯ»ЇЯ«ЋЯ»Є Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е? Я«ЄЯ«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»ЄЯ«»Я»Є Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«ЄЯ«цЯ»ЂЯ«хЯ»Є Я«еЯ««Я»ЇЯ««Я»ЂЯ«ЪЯ»ѕЯ«» Я«ЋЯ»іЯ«ЪЯ«┐ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«ЄЯ«ЪЯ««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»ЂЯ««Я»Ї Я«ЄЯ«цЯ«ЕЯ»ІЯ«ЪЯ»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»ЂЯ«ЪЯ»ѕЯ«» Я««Я«▒Я»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«фЯ»Ї Я«фЯ»ЄЯ«џЯ«▓Я«ЙЯ««Я»Ї. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї, Я«ЄЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«еЯ»ђЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЄЯ«░Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕ Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я«▓Я»ЇЯ«▓Я«ЙЯ««Я«▓Я»Ї Я«ЁЯ«цЯ»ѕЯ«хЯ«┐Я«Ъ Я«ЁЯ«цЯ«┐Я«ЋЯ««Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«еЯ«ЙЯ««Я»Ї Я«хЯ«▓Я«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї 2 Я«ЁЯ«▓Я«ЋЯ»ЂЯ««Я»Ї Я««Я»ЄЯ«▓Я»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї 3 Я«ЁЯ«▓Я«ЋЯ»ЂЯ««Я»Ї Я«џЯ»єЯ«▓Я»ЇЯ«хЯ«цЯ«ЙЯ«Ћ Я«еЯ«┐Я«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї Я«еЯ«ЙЯ««Я»Ї Я«ЄЯ«еЯ»ЇЯ«ц Я«ЄЯ«ЪЯ«цЯ»ЇЯ«цЯ»ѕ (Рєњ 2, РєЉ 3) Я«јЯ«Е
Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ, Я«ЋЯ«┐Я«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕ, Я««Я»ЄЯ«▓Я»Ї, Я«ЋЯ»ђЯ«┤Я»Ї ... Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«хЯ«цЯ»Ђ Я«јЯ«│Я«┐Я«цЯ«▓Я»ЇЯ«▓. Я«јЯ«ЕЯ«хЯ»Є, Я«ЄЯ«цЯ»ѕ Я«еЯ«ЙЯ««Я»Ї Я«џЯ»ЂЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«Ћ (2, 3) Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«▒Я»ЂЯ«хЯ»ІЯ««Я»Ї. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«хЯ«▓Я«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї 2 Я«ЁЯ«▓Я«ЋЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЄЯ«▒Я»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї 3 Я«ЁЯ«▓Я«ЋЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»ЂЯ«░Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я»ІЯ««Я»Ї.
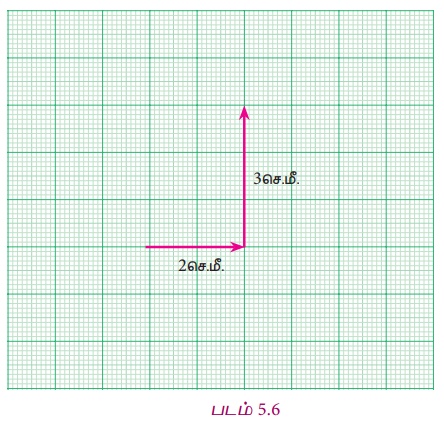
Я«еЯ«ЙЯ««Я»Ї Я««Я»ЂЯ«цЯ«▓Я«┐Я«▓Я»Ї 3 Я«ЁЯ«▓Я«ЋЯ»Ђ Я««Я»ЄЯ«▒Я»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 2 Я«ЁЯ«▓Я«ЋЯ»Ђ Я«хЯ«▓Я«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї Я«џЯ»єЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЁЯ«ЪЯ»ѕЯ«еЯ»ЇЯ«ц Я«ЄЯ«ЪЯ««Я«ЙЯ«Е (2, 3) Я«ЄЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«хЯ«┤Я«┐Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ЂЯ««Я»Ї (3, 2) Я«ЄЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«хЯ«┤Я«┐Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«ЋЯ»ЂЯ««Я«Й? Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«Ћ. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, ( Рѕњ2, 3) Я«јЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї? Я«ЄЯ«цЯ»Ђ Я«јЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»ЂЯ««Я»Ї (0, 0) Я«ЄЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 2 Я«ЁЯ«▓Я«ЋЯ»Ђ Я«ЄЯ«ЪЯ«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 3 Я«ЁЯ«▓Я«ЋЯ»Ђ Я««Я»ЄЯ«▒Я»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї. (2, Рѕњ3) Я«ЄЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«хЯ«┤Я«┐Я««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ»ЇЯ«Е? Я«ЄЯ«цЯ»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЂЯ«хЯ«цЯ»Ђ 2 Я«ЁЯ«▓Я«ЋЯ»Ђ Я«хЯ«▓Я«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї 3 Я«ЁЯ«▓Я«ЋЯ»Ђ Я«ЋЯ»ђЯ«┤Я»ЇЯ«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї. Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«јЯ«БЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ»єЯ«»Я«░Я«┐Я«ЪЯ«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«» Я«цЯ»ЄЯ«хЯ»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«ЋЯ«┐Я«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕ Я«јЯ«БЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕ x
Я«ЁЯ«џЯ»ЇЯ«џЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«јЯ«БЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕ y
Я«ЁЯ«џЯ»ЇЯ«џЯ»Ђ Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЁЯ«┤Я»ѕЯ«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я«хЯ«▓Я«фЯ»ЇЯ«фЯ»ЂЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї X Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ«фЯ»ЇЯ«фЯ»ЂЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї X' Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я««Я»ЄЯ«▓Я»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї Y Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ»ђЯ«┤Я»ЇЯ«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї Y' Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
x РѕњЯ«єЯ«»Я«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕ Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ (abscissa) Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї y
Я«єЯ«»Я«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ (ordinate) Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«єЯ«» Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ«│Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ (0,0) Я«љ Я«єЯ«цЯ«┐ (origin) Я«јЯ«ЕЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
(0,0) Я«љЯ«цЯ»Ї Я«цЯ«ЙЯ«│Я«┐Я«ЕЯ»Ї Я««Я»ѕЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«хЯ»ЄЯ«▒Я»Ђ Я«јЯ«ЎЯ»ЇЯ«ЋЯ»ЄЯ«»Я»І Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«фЯ»іЯ«░Я»ЂЯ«ЪЯ»ЇЯ«ЪЯ«▓Я»ЇЯ«▓. Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«јЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»ЂЯ««Я»Ї (0,0) Я«єЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, Я«ЁЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Є Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«јЯ«▓Я»ЇЯ«▓Я«Й Я«хЯ«┤Я«┐Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЂЯ««Я»Ї Я«єЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕ O Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЂЯ«хЯ»ІЯ««Я»Ї.
Я«еЯ«ЙЯ««Я»Ї Я«ЄЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«цЯ«ЙЯ«│Я«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я«јЯ«еЯ»ЇЯ«цЯ«хЯ»іЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕЯ«»Я»ЂЯ««Я»Ї (x,y)
Я«јЯ«Е Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї. Я«јЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я«ЙЯ«»Я«┐Я«ЕЯ»ЂЯ««Я»Ї Я«еЯ««Я»ЇЯ««Я»ЂЯ«ЪЯ»ѕЯ«» Я«цЯ«ЙЯ«│Я«┐Я«▓Я»Ї 1, 2, .... Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«цЯ»Ђ Я«јЯ«цЯ»ѕ? Я«ЄЯ«еЯ»ЇЯ«ц Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«Ъ Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«┐Я«▓ Я«фЯ»іЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ««Я«ЙЯ«Е Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ»ЄЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»єЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«» Я«цЯ»ЄЯ«хЯ»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, Я«еЯ«ЙЯ««Я»Ї 1 Я«ЁЯ«▓Я«ЋЯ»ѕ 1 Я«џЯ»є.Я««Я»ђ. Я«јЯ«ЕЯ«цЯ»Ї Я«цЯ»ЄЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»єЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я«єЯ«ЋЯ«хЯ»Є, (0,0) РѕњЯ«ЋЯ»ЇЯ«ЋЯ»Ђ
Я«хЯ«▓Я«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я«ЙЯ«Ћ 2 Я«џЯ»є.Я««Я»ђ. Я«еЯ«ЋЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЄЯ«▓Я»ЇЯ«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ 3 Я«џЯ»є.Я««Я»ђ. Я«еЯ«ЋЯ«░Я»ЇЯ«цЯ«▓Я»Є (2,3) Я«ЄЯ«ЕЯ»Ї Я«хЯ«┤Я«┐Я««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ»ЄЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»єЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ«ЕЯ»ЇЯ«ЕЯ«┐Я«џЯ»ЇЯ«џЯ»ѕЯ«»Я«ЙЯ«ЕЯ«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ«┐Я«▓Я»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.
Я«еЯ«ЙЯ««Я»Ї 1 Я«ЁЯ«▓Я«ЋЯ»ѕ 2 Я«џЯ»є.Я««Я»ђ. Я«јЯ«Е Я«јЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ»ІЯ««Я»ЄЯ«»Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«┐Я«ЋЯ«фЯ»Ї Я«фЯ»єЯ«░Я«┐Я«»Я«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│ Я«цЯ»ѓЯ«░Я««Я»Ї Я«јЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»ЂЯ««Я»Ї Я««Я«ЙЯ«▒Я«ЙЯ«цЯ»Ђ. Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«еЯ««Я»ЇЯ««Я«┐Я«ЪЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ Я«хЯ»єЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ«ЙЯ«ЋЯ«┐Я«цЯ««Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓. Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«јЯ«БЯ»ЇЯ«БЯ«▒Я»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕ Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»іЯ«┤Я«┐ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
x Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ««Я»Ї y
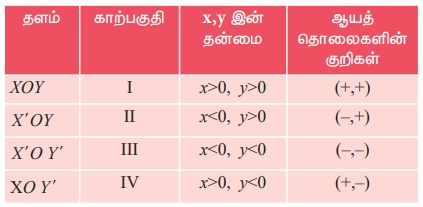
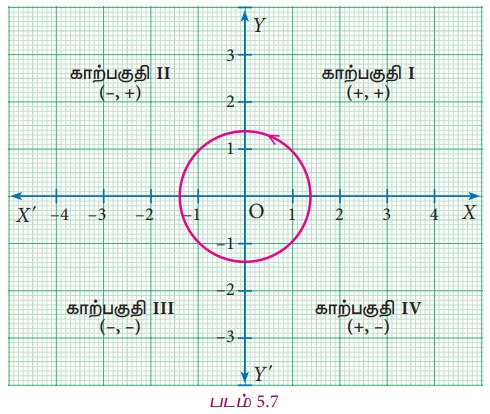
Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ««Я»Ї Я«цЯ«│Я«цЯ»ЇЯ«цЯ»ѕ Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«ЋЯ«│Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«┐Я«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«еЯ«ЙЯ««Я»Ї Я«ЋЯ«ЙЯ«▒Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«ЋЯ«│Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ»ІЯ««Я»Ї. (Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«Ћ: Я«еЯ«ЙЯ«▒Я»ЇЯ«ЋЯ«░Я««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«цЯ»Ђ. Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ«ЙЯ«▒Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«ЋЯ«│Я»Ї) Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Ћ, Я«ЁЯ«хЯ»ѕ I,
II, III Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї
IV Я«јЯ«Е Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЪЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«┐Я«▓Я»Ї I Я«єЯ«ЕЯ«цЯ»Ђ Я«ЋЯ«┐Я«┤Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▒Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я»ѕЯ«»Я»ЂЯ««Я»Ї, II Я«єЯ«ЕЯ«цЯ»Ђ Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▓Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я»ѕЯ«»Я»ЂЯ««Я»Ї, III Я«єЯ«ЕЯ«цЯ»Ђ Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«ЋЯ»ђЯ«┤Я»ЇЯ«фЯ»Ї Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я»ѕЯ«»Я»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї, IV Я«єЯ«ЕЯ«цЯ»Ђ Я«ЋЯ«┐Я«┤Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ђЯ«┤Я»ЇЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ«ЪЯ«┐Я«ЋЯ«ЙЯ«░ Я«јЯ«цЯ«┐Я«░Я»ЇЯ«џЯ»ЇЯ«џЯ»ЂЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я»Ї Я«фЯ«»Я«БЯ«цЯ»ЇЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
Я«ЄЯ«еЯ»ЇЯ«ц Я«хЯ«┤Я«┐Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕ (Я«ЋЯ«ЪЯ«┐Я«ЋЯ«ЙЯ«░ Я«јЯ«цЯ«┐Я«░Я»Ї Я«џЯ»ЂЯ«▒Я»ЇЯ«▒Я»Ђ) Я«ЋЯ«ЪЯ«┐Я«ЋЯ«ЙЯ«░Я«џЯ»Ї Я«џЯ»ЂЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«ЙЯ««Я«▓Я»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«хЯ»ЄЯ«▒Я»Ђ Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«ЋЯ«ЙЯ«▒Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»І Я«цЯ»іЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я«Й? Я«ЄЯ«цЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»іЯ«░Я»ЂЯ«ЪЯ»ЇЯ«ЪЯ«▓Я»ЇЯ«▓, Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї, Я«ЄЯ«цЯ»Ђ Я«џЯ«┐Я«▓ Я«еЯ»ѓЯ«▒Я»ЇЯ«▒Я«ЙЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЕЯ»ЇЯ«фЯ«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Є Я«еЯ««Я»ЇЯ««Я«ЙЯ«▓Я»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«фЯ«▒Я»ЇЯ«▒Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«џЯ«┐Я«▓ Я«џЯ«┐Я«▒Я«еЯ»ЇЯ«ц Я«хЯ«┤Я«┐Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
Рђб x Я«ЁЯ«џЯ»ЇЯ«џЯ«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«јЯ«еЯ»ЇЯ«ц Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ P Я«»Я«┐Я«ЕЯ»Ї y Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, P (x,0).
Рђб y Я«ЁЯ«џЯ»ЇЯ«џЯ«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«јЯ«еЯ»ЇЯ«ц Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Q Я«ЄЯ«ЕЯ»Ї x Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, Q (0, y)
Рђб (x, y) РЅа (y, x) ; x Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y Я«џЯ««Я««Я«▓Я»ЇЯ«▓
Рђб Я«џЯ»єЯ«хЯ»ЇЯ«хЯ«Ћ Я«єЯ«» Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЅЯ«ЪЯ»ѕЯ«» Я«цЯ«│Я««Я»Ї Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«цЯ«│Я««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
1. Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«цЯ»ЇЯ«цЯ«▓Я»Ї (Plotting Points in Cartesian Coordinate Plane)
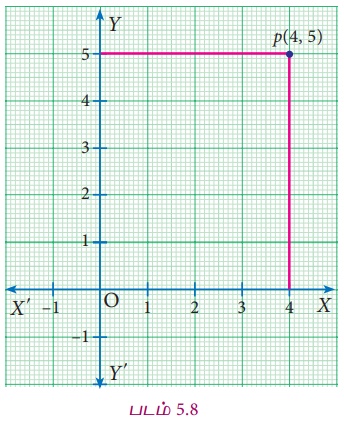
(4,5)
Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«єЯ«» Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«цЯ»Ї Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«Ћ, x Я«ЁЯ«џЯ»ЇЯ«џЯ«┐Я«▓Я»Ї 4 Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«еЯ«ЋЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»Ђ, Я«ЁЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»Ђ x
= 4 Я«хЯ«░Я»ѕЯ«Ћ.
Я«ЄЯ«цЯ»Є Я«фЯ»ІЯ«▓Я»Ї y
Я«ЁЯ«џЯ»ЇЯ«џЯ«┐Я«▓Я»Ї 5 Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«еЯ«ЋЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ««Я«ЪЯ»ЇЯ«ЪЯ««Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»Ђ y
= 5 Я«хЯ«░Я»ѕЯ«Ћ.
Я«ЄЯ«еЯ»ЇЯ«ц Я«ЄЯ«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ««Я»Ї Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ (4,5) Я«ЄЯ«ЕЯ»Ї Я«ЄЯ«ЪЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«ЙЯ«ЕЯ«цЯ»Ђ x
Я«ЁЯ«џЯ»ЇЯ«џЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 5 Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▓Я»ЂЯ««Я»Ї y
Я«ЁЯ«џЯ»ЇЯ«џЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 4 Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▓Я»ЂЯ««Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї. Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї (4,5) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.1
Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»Ї Я«јЯ«еЯ»ЇЯ«цЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«▒Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї?
(Я«Ё)
(3, Рѕњ8)
(Я«є)
( Рѕњ1, Рѕњ3)
(Я«Є)
(2, 5)
(Я«ѕ)
( Рѕњ7, 3)
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
(Я«Ё)
x Рѕњ Я«єЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕ Я««Я«┐Я«ЋЯ»ѕ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y
Рѕњ Я«єЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕ Я«ЋЯ»ЂЯ«▒Я»ѕ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ. Я«јЯ«ЕЯ«хЯ»Є, (3, Рѕњ8) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ IV Я«єЯ«хЯ«цЯ»Ђ Я«ЋЯ«ЙЯ«▒Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї.
(Я«є)
x РѕњЯ«єЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕ Я«ЋЯ»ЂЯ«▒Я»ѕ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y
РѕњЯ«єЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕ Я«ЋЯ»ЂЯ«▒Я»ѕ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ. Я«јЯ«ЕЯ«хЯ»Є, ( Рѕњ1, Рѕњ3) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ III Я«єЯ«хЯ«цЯ»Ђ Я«ЋЯ«ЙЯ«▒Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї.
(Я«Є)
x РѕњЯ«єЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕ Я««Я«┐Я«ЋЯ»ѕ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y
РѕњЯ«єЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕ Я««Я«┐Я«ЋЯ»ѕ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ. Я«јЯ«ЕЯ«хЯ»Є, (2,5) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ I
Я«єЯ«хЯ«цЯ»Ђ Я«ЋЯ«ЙЯ«▒Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї.
(Я«ѕ)
x РѕњЯ«єЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕ Я«ЋЯ»ЂЯ«▒Я»ѕ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y
Рѕњ Я«єЯ«»Я«цЯ»ЇЯ«цЯ»іЯ«▓Я»ѕ Я««Я«┐Я«ЋЯ»ѕ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ. Я«јЯ«ЕЯ«хЯ»Є, ( Рѕњ7 , 3) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ II Я«єЯ«хЯ«цЯ»Ђ Я«ЋЯ«ЙЯ«▒Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.2
A(2, 4) , B( Рѕњ 3, 5), C(Рѕњ 4, Рѕњ 5), Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї D(4, Рѕњ 2) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
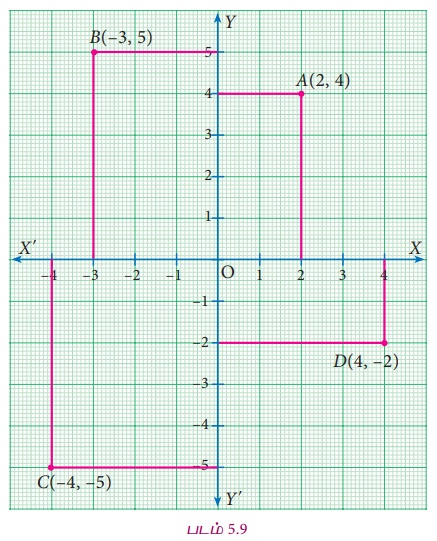
(i) (2,4) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«Ћ, x = 2 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y
= 4 Я«јЯ«ЕЯ»ЇЯ«▒
Я«ЋЯ«┐Я«ЪЯ»ѕЯ««Я«ЪЯ»ЇЯ«ЪЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ«░Я»ѕЯ«Ћ. Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ (2,4) Я«ЄЯ«ЕЯ»Ї Я«ЁЯ««Я»ѕЯ«хЯ«┐Я«ЪЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ««Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї A(2,4) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«▒Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐ I Я«ЄЯ«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
(ii) ( Рѕњ 3, 5) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«Ћ, x = Рѕњ 3 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y
= 5 Я«јЯ«ЕЯ»ЇЯ«▒
Я«ЋЯ«┐Я«ЪЯ»ѕЯ««Я«ЪЯ»ЇЯ«ЪЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ«░Я»ѕЯ«Ћ. Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ ( Рѕњ 3 , 5) Я«ЄЯ«ЕЯ»Ї Я«ЁЯ««Я»ѕЯ«хЯ«┐Я«ЪЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ««Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї B( Рѕњ 3 , 5) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«▒Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐ II Я«ЄЯ«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
(iii) ( Рѕњ 4, Рѕњ 5) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«Ћ, x = Рѕњ 4 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y
= Рѕњ 5 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ«┐Я«ЪЯ»ѕЯ««Я«ЪЯ»ЇЯ«ЪЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ«░Я»ѕЯ«Ћ. Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ ( Рѕњ 4 , Рѕњ 5) Я«ЄЯ«ЕЯ»Ї Я«ЁЯ««Я»ѕЯ«хЯ«┐Я«ЪЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ««Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї C( Рѕњ 4 , Рѕњ 5) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«▒Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐ III Я«ЄЯ«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«ЕЯ»Ї x Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ««Я«ЙЯ«▒Я»ЇЯ«▒Я««Я»Ї Я«џЯ»єЯ«»Я»ЇЯ«цЯ«ЙЯ«▓Я»Ї Я«ЁЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«хЯ»ЄЯ«▒Я»іЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«ЁЯ««Я»ѕЯ«хЯ«┐Я«ЪЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЂЯ««Я»Ї. Я«јЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«ЁЯ«хЯ»ѕ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«јЯ«ЕЯ«џЯ»Ї Я«џЯ«┐Я«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«Ћ!
(iv) (4, Рѕњ2) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«Ћ, x = 4 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y
= Рѕњ2 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ«┐Я«ЪЯ»ѕЯ««Я«ЪЯ»ЇЯ«ЪЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ«░Я»ѕЯ«Ћ. Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ (4 , Рѕњ2) Я«ЄЯ«ЕЯ»Ї Я«ЁЯ««Я»ѕЯ«хЯ«┐Я«ЪЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ««Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї D(4 , Рѕњ2) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«▒Я»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐ IV Я«ЄЯ«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.3
A(2,2), B( Рѕњ2,2), C( Рѕњ2, Рѕњ1), Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї D(2, Рѕњ1) Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«░Я»ЇЯ«ЪЯ»ЇЯ«ЪЯ»ђЯ«џЯ«┐Я«»Я«ЕЯ»Ї Я«цЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї. Я«ЁЯ«еЯ»ЇЯ«цЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐ Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«хЯ«ЪЯ«┐Я«хЯ«цЯ»ЇЯ«цЯ»ѕ Я«хЯ«┐Я«хЯ«ЙЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
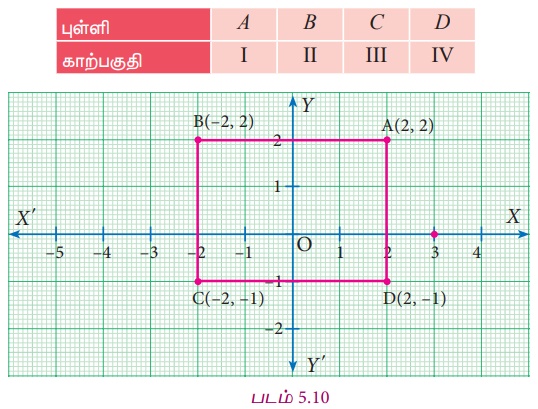
ABCD Я«њЯ«░Я»Ђ
Я«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«џЯ»ЇЯ«џЯ»єЯ«хЯ»ЇЯ«хЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї, Я«ЁЯ«ЋЯ«▓Я««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ«│Я«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«Б Я««Я»ЂЯ«ЪЯ«┐Я«»Я»ЂЯ««Я«Й?
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
x РѕњЯ«ЁЯ«џЯ»ЇЯ«џЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЄЯ«БЯ»ѕЯ«»Я«ЙЯ«Е Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї y Рѕњ Я«ЁЯ«џЯ»ЇЯ«џЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«хЯ»Ђ Я«џЯ««Я««Я«ЙЯ«ЕЯ«цЯ«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї.