வெக்டர்களின் மீதான இயற்கணிதம் (Algebra of Vectors)

வெக்டர்களின் மீதான இயற்கணிதம் (Algebra of Vectors)

மெய்யெண்கள் அல்லது அணிகளின் மீதான செயல் முறைகள் போன்றே நாம் வெக்டர்களின் மீதும் செயல்முறைகளைக் காணலாம். இரண்டு வெக்டர்களின் கூட்டல், ஒரு வெக்டரிலிருந்து மற்றொரு வெக்டரைக் கழித்தல் மற்றும் ஒரு வெக்டரை ஒரு திசையிலி கொண்டு பெருக்குதல் போன்றவற்றைக் காண்போம்.

1. வெக்டர்களின் கூட்டல் (Addition of Vectors)

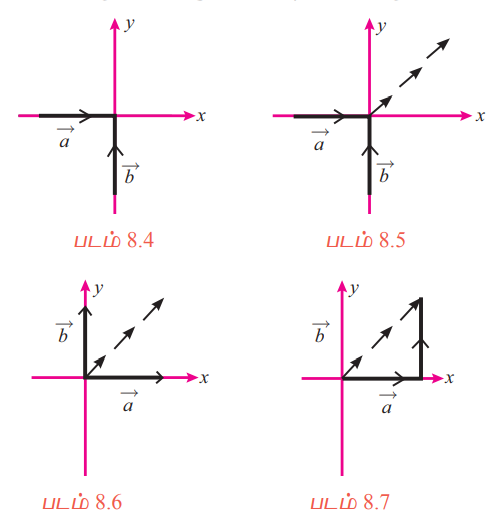
வெக்டர்களின் கூட்டலை இரண்டு வகைகளில் வரையறுத்து அவை ஒன்றே எனக் காண்போம். ஓரலகு நிறை கொண்ட ஒரு பொருள் ℝ2−ல் (0, 0) என்ற இடத்தில் உள்ளது என்க. அதன் அளவை ஒரு புள்ளி என எடுத்துக்கொள்வோம். இரண்டு ஓரலகு விசைகள் 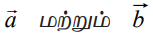 ஆகியவை x−அச்சு மற்றும்  y−அச்சின் மிகைத் திசையில் அப்பொருளின் மீது செயல்படுவதாகக் கொள்க. (படம் 8.4−ஐ பார்க்க). இப்பொழுது அப்பொருளானது x − அச்சுடன் 45° கோணத்தில் படம் 8.5.−ல் உள்ளது போல் நகரும் என எளிதில் கணிக்கலாம். 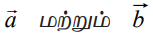என்ற விசைகள் 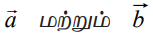என்ற வெக்டர்களால் படம் 8.6−ல் குறிப்பிடப்பட்டுள்ளது. விசைகள் படம் 8.4−ல் அப்பொருளை தள்ளுவதாகவும் படம் 8.6−ல் அப்பொருளை இழுப்பதாகவும் நாம் கருதலாம்.

அடுத்து நமக்குத் தோன்றும் கேள்வி, “அது எவ்வளவு தூரம் நகரும்?” என்பதாகும். விசைகள் ஒன்றன்பின் ஒன்றாகச் செயல்படுவதாகக் கருதுவோம். விசை −ஆனது அப்பொருளை x−அச்சின் திசையில் ஓரலகு தூரம் நகர்த்தும். எனவே அந்தப் பொருள் (0, 0)−ல் இருந்து (1, 0) என்ற புள்ளிக்கு நகர்கின்றது. இப்பொழுது விசை ஆனது அப்பொருளைச் செங்குத்தாக மேல்நோக்கி (1, 0) என்ற புள்ளியில் இருந்து (1, 1) என்ற புள்ளிக்கு நகர்த்துகின்றது. இறுதியாக அப்பொருள் (1, 1)−ல் உள்ளது. (படம் 8.7ஐ பார்க்க). எனவே இரண்டு வெக்டர்களின் கூடுதலானது (0, 0) மற்றும் (1, 1)−ஐ இணைக்கும் கோட்டுத்துண்டாக (0, 0)−லிருந்து (1,1) என்ற திசையில் வரையறுக்கப்படுகிறது.

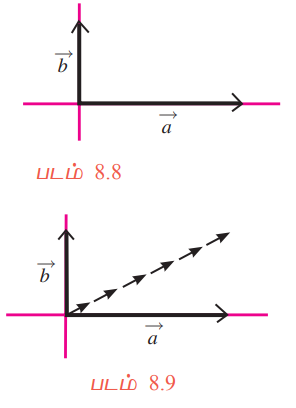
இப்பொழுது மேற்கூறிய சூழ்நிலையில் −ன் எண்ணளவையை 1−க்குப் பதில் 2 எனக் கொள்க. (படம் 8.8−ஐ பார்க்க). படம் 8.9−ல் உள்ளபடி அப்பொருளானது x−அச்சுக்கு அருகில் நகரும் என எளிதில் கணிக்கலாம். மேலும் அப்பொருளானது (2,1) என்ற புள்ளிக்கு நகரும் என்பதையும் கணிக்கலாம். எனவே இந்த இரண்டு வெக்டர்களின் கூடுதலானது (0,0)−வையும் (2,1)−ஐயும் இணைக்கும் கோட்டுத்துண்டினால் “(0,0)−விலிருந்து (2,1) என்ற திசையில் வரையறுக்கப்படுகின்றது”.

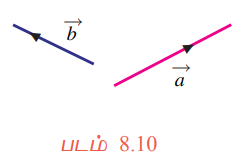
இந்த இரண்டு சூழ்நிலைகளிலும் விசைகள் ஒன்றுக்கொன்று செங்குத்தாக இருந்தன. ஆனால் பொதுவாக விசைகள் செங்குத்தாக இருக்கவேண்டிய அவசியமில்லை. இருந்தபோதிலும் ஒன்றன்பின் ஒன்றாகச் செயல்படும் விசைகளைக் கூட்ட இயலும். உதாரணமாக 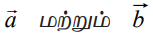என்ற விசைகளை படம் 8.10−ல் உள்ளது போன்று கருதுக.

−ன் இறுதிப்புள்ளியுடன்  −ன் ஆரம்பப்புள்ளி அமையுமாறு (படம் 8.11) அமைக்க.

இவற்றின் கூடுதலானது படம் 8.12−ல் உள்ளது போன்று கிடைக்கிறது. நாம் இப்பொழுது இரண்டு வெக்டர்களுக்கான கூடுதலின் வரையறையைக் காண்போம்.

வெக்டர் கூட்டலின் முக்கோணவிதி (Triangle law of addition)

வரையறை 8.10 (வெக்டர் கூட்டலின் முக்கோண விதி)

இரு வெக்டர்கள் அவற்றின் எண்ணளவாலும் திசையாலும் ஒரு முக்கோணத்தின் வரிசையாக எடுக்கப்பட்ட இரண்டு பக்கங்களின் மூலமாகக் குறிப்பிட்டால், அவற்றின் கூடுதலை அம்முக்கோணத்தின் எதிர் வரிசையில் எடுக்கப்பட்ட மூன்றாவது பக்கத்தினால் குறிக்கலாம்.

முடிவு 8.1

வெக்டர் கூட்டலின் இணைகர விதி (Parallelogram law of vector addition)

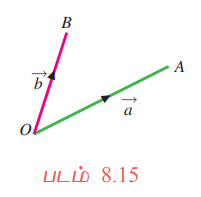
என்பன ஏதேனும் இரு வெக்டர்கள் என்க. இந்த இரு வெக்டர்களின் தொடக்கப் புள்ளிகளை (O) ஒன்றாகக் கொண்டு, வரையறை 8.7−ஐப் பயன்படுத்தி கூடுதலைக் காண்போம். A மற்றும் B ஆகியவை ஆகியவற்றின் முடிவுப்புள்ளிகள் (படம் 8.15) என்க.

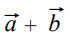  −ஐக் காண, AC−ஐ OB−க்கு இணையாக OB= AC என்றவாறு வரைக. இங்கு என்பது இவற்றின் கூடுதலாகும். (படம் 8.16). 

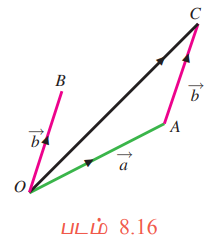
இங்கு OA மற்றும் BC ஆகியவை இணை என்பதைக் கவனிக்க (படம் 8.17).

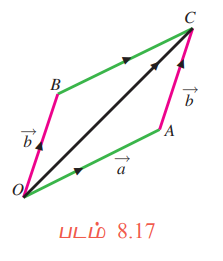
எனவே ஒரே தொடக்கப் புள்ளிகளை உடைய இரு வெக்டர்களின் கூடுதலைக் காண இந்த வெக்டர்களை அடுத்தடுத்த பக்கங்களாகக் கொண்டு ஓர் இணைகரம் வரைந்து அதன் மூலை விட்டத்தை அதன் கூடுதல் என்கிறோம். ஒரே தொடக்கப்புள்ளியைக் கொண்டில்லாத இரு வெக்டர்களை ஏதேனும் ஒரு வெக்டரைத் தகுந்தவாறு நகர்த்தி ஒரே தொடக்கப்புள்ளியினை உடைய வெக்டர்களாக மாற்றலாம். இதிலிருந்து கீழ்க்காணும் வரையறை 8.11−ஐ பெறலாம்.

O என்ற ஒரே தொடக்கப்புள்ளியை உடைய இரு வெக்டர்கள் 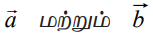என்க. இவற்றின்  இறுதிப்புள்ளிகள் முறையே A மற்றும் Bஎன்க.

OACB என்ற இணைகரத்தை பூர்த்தி செய்க. 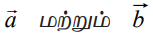−ன் கூடுதலானது என வரையறுக்கப்படுகிறது.

வரையறை 8.11 (கூட்டலின் இணைகர விதி)

OABC என்ற இணைகரத்தில் மற்றும் ஆகியவை அடுத்தடுத்த பக்கங்களைக் குறித்தால், அதன் மூலைவிட்டமான இவற்றின் கூடுதலைக் குறிக்கும் (படம் 8.17−ஐ பார்க்க).

வெக்டர் கூட்டலுக்கு இரண்டு வகையான வரையறைகள் இருந்தபோதிலும் அவை இரண்டும் ஒன்றே ஆகும். வரையறை 8.10 ஆனது வெக்டர் கூட்டலின் முக்கோண விதியையும் வரையறை 8.11 ஆனது வெக்டர் கூட்டலின் இணைகர விதியையும் கூறுகிறது.

முக்கோணம் ABC−ல் 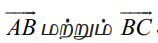ஆகியவை இரண்டு பக்கங்களைக் குறித்தால், மூன்றாவது பக்கம் ஆனது அதன் கூடுதலைக் குறிக்கின்றது.

2. இரண்டு வெக்டர்களுக்கிடையேயான வித்தியாசம் (Difference between two Vectors)

இப்பொழுது ஒரு வெக்டரிலிருந்து மற்றொரு வெக்டரை கழிக்கும் முறையைக் காண்போம்.

வரையறை 8.12

வெக்டர்களின் வித்தியாசத்திற்கான வடிவக் கணித விளக்கம் (Geometrical interpretation of difference between two vectors)

என்ற வெக்டரின் ஆரம்பப் புள்ளி P மற்றும் முடிவுப்புள்ளி Q என்க. என்ற வெக்டரின் ஆரம்பப்புள்ளி Q மற்றும் முடிவுப்புள்ளி P என்க. இந்த இரு வெக்டர்களின் எண்ணளவைகள் P மற்றும் Q என்ற புள்ளிகளை இணைக்கும் கோட்டுத்துண்டின் நீளம் ஆகும். எனவே இவற்றின் எண் அளவைகள் சமம். ஆனால் இவற்றின் திசைகள் நேர் எதிரானவை. எனவே −ஆனது − −க்குச் சமம் ஆகும்.

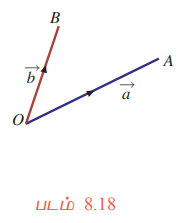
நாம் இதனை வடிவியலின் துணைகொண்டு பார்க்கலாம். 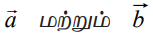ஆகியவை முறையே மற்றும் ஆகியவற்றைக் குறிக்கிறது என்க. (படம் 8.18). 

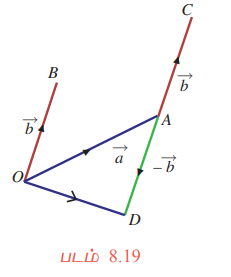
ACயை OBக்கு இணையாக AC = OBஎனுமாறு வரைக. இப்பொழுது  என்பது   −க்குச் சமமாக இருக்கும். CA = AD எனுமாறு CA என்ற கோட்டை D வரை நீட்டுக. இப்பொழுது க்கு சமம் ஆகும்.

3. வெக்டரின் திசையிலிப் பெருக்கல் (Scalar multiplication of a vector)

நாம் இப்பொழுது ஒரு வெக்டரை ஒரு திசையிலியால் எவ்வாறு பெருக்குவது என்பதைக் காண்போம்.

என்பது ஏதேனும் ஒரு வெக்டர், m ஒரு திசையிலி என்க. m என்பது வெக்டர் −யுடன் திசையிலி m−ன் திசையிலிப் பெருக்கம் என்கிறோம்.

m பூஜ்ஜியம் எனில், m −ன் எண்ணளவு 0 ஆகும். எனவே m என்பது பூஜ்ஜிய வெக்டர் ஆகும். m மிகை எண் எனில், மற்றும் m ஆகியவை ஒரே திசையைக் குறிப்பதாகவும் m குறை எண் எனில், மற்றும் m ஆகியவை எதிர் திசையைக் குறிப்பதாகவும் அமையும். ஆகவே m மிகை எண் எனில் மற்றும் m ஆகியவை ஒரே திசை வெக்டர்கள் ஆகவும், m குறை எண் எனில் மற்றும் m ஆகியவை எதிர் திசை வெக்டர்கள் ஆகவும் அமையும். 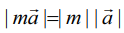ஆகும். 

வரையறை 8.13

மற்றும் என்ற இரு வெக்டர்கள் இணை எனில் ஏதேனும் ஒரு திசையிலி λ −க்கு = λ என அமையும். λ > 0 எனில், அவை ஒரே திசையிலும், λ < 0 எனில், அவை எதிர்த்திசையிலும் அமையும்.

4. சில பண்புகளும் முடிவுகளும் (Some Properties and results) 

ஏதேனும் இரு வெக்டர்கள் மற்றும் திசையிலிகள் m, nக்கு

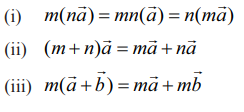
முடிவு 8.2

வெக்டர் கூட்டல் சேர்ப்புப் பண்பு உடையது.

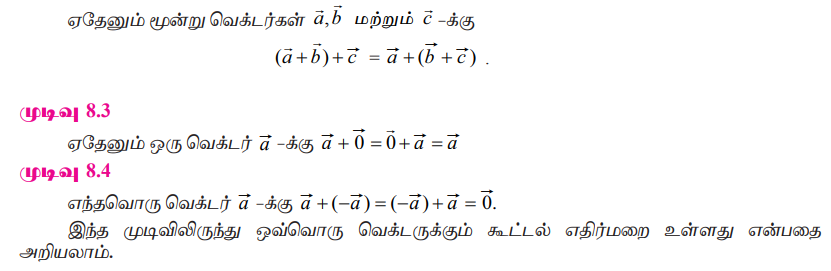
முடிவு 8.5

வெக்டர்களின் கூட்டல் பரிமாற்று விதியை நிறைவு செய்யும்.

நிரூபணம்

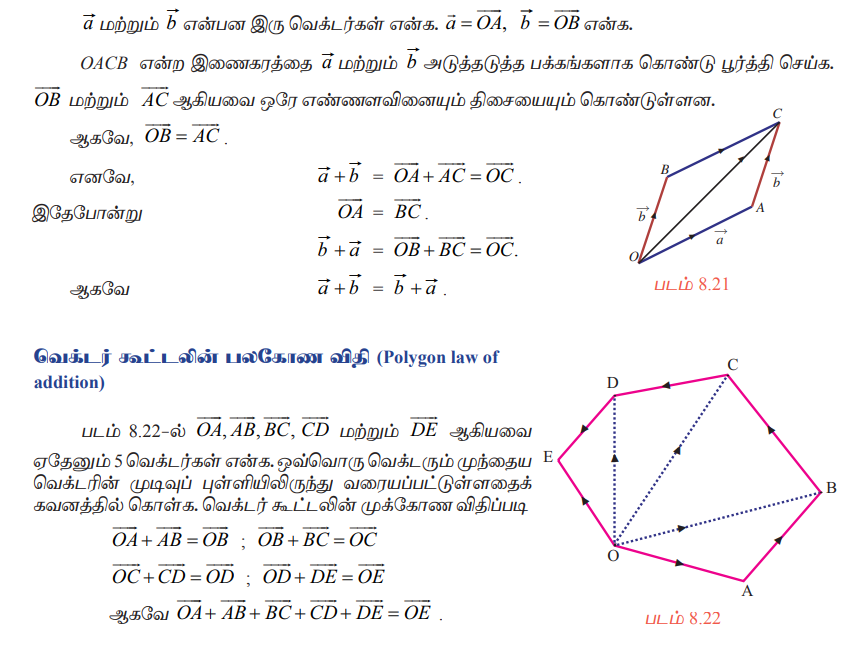
எனவே அனைத்து வெக்டர்களின் கூடுதலானது முதல் வெக்டரின் தொடக்கப்புள்ளியைக் கடைசி வெக்டரின் முடிவுப்புள்ளியுடன் இணைக்கும் வெக்டராகும். இதனை வெக்டர் கூட்டலின் பலகோண விதி என்கிறோம்.

எடுத்துக்காட்டு 8.1

வரைபடத்தின் வாயிலாகக் கீழ்க்காணும் இடப்பெயர்ச்சியைக் குறிக்க. 

(i) 30 கி.மீ., 60° வடக்கிலிருந்து மேற்காக

(ii) 60 கி.மீ., 50° கிழக்கிலிருந்து தெற்காக

தீர்வு

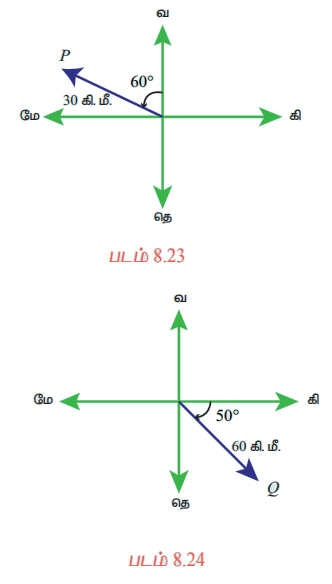
எடுத்துக்காட்டு 8.2

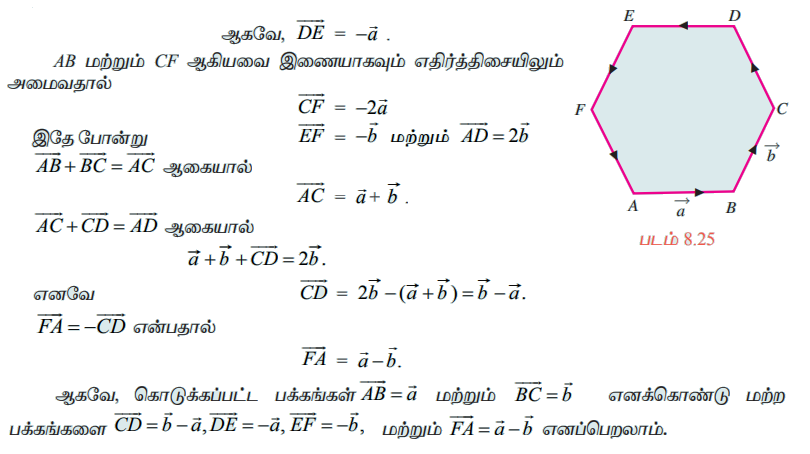
ஓர் ஒழுங்கு அறுகோணத்தின் இரண்டு அடுத்தடுத்த பக்கங்கள் ,  ஆக இருந்தால் பிற பக்கங்களைக் குறிக்கும் வெக்டர்களைக் காண்க.

தீர்வு 

A,B,C,D,E,F ஆகியவை ஒழுங்கு அறுகோணத்தின் முனைப்புள்ளிகள் என்க.

.

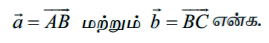ஒழுங்கு அறுகோணத்தின் கீழ்க்காணும் பண்புகளை பயன்படுத்தி பக்கங்களைக் காணலாம்.

(i) AB, CF மற்றும் ED ஆகியவை இணையானவை. மேலும், BC, AD மற்றும் EF ஆகியவையும் இணை ஆகும்.

(ii) CF−ன் நீளம் AB−ன் நீளத்தைப் போல் இரண்டு மடங்கு மற்றும் AD−ன் நீளம் BC−ன் நீளத்தைப் போல் இரண்டு மடங்கு ஆகும்.

ABமற்றும் DE ஆகியவை இணையானவை. நீளங்கள் சமமாகவும் திசை எதிர்த் திசையாகவும் உள்ளன.