வரையறை, தேற்றம், எடுத்துக்காட்டு கணக்குகள் | கணக்கு - நிலை வெக்டர்கள் (Position vectors) | 11th Mathematics : UNIT 8 : Vector Algebra I
11 வது கணக்கு : அலகு 8 : வெக்டர் இயற்கணிதம் (Vector Algebra)
நிலை வெக்டர்கள் (Position vectors)
நிலை வெக்டர்கள் (Position vectors)
வரையறை 8.14
O வை ஆதியாகக் கொள்க. மற்றும் ஏதேனும் ஒரு புள்ளி P−ஐ (தளத்திலோ அல்லது முப்பரிமாண வெளியிலோ) குறிக்கவும். இப்பொழுது ![]() −ஆனது O வைப் பொறுத்து P−ன் நிலைவெக்டர் என்று அழைக்கப்படுகின்றது.
−ஆனது O வைப் பொறுத்து P−ன் நிலைவெக்டர் என்று அழைக்கப்படுகின்றது.
வெக்டருக்கும் நிலை வெக்டர்களுக்கும் இடையேயான தொடர்பைக் கீழ்க்காணுமாறு வரையறுக்கலாம்.
முடிவு 8.6
O−வை ஆதி என்க. மேலும் A மற்றும் B−யை ஏதேனும் இரு புள்ளிகள் என்க. இப்போது 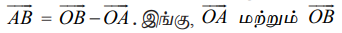 . ஆகியவை A மற்றும் B−ன் நிலை வெக்டர்களாகும்.
. ஆகியவை A மற்றும் B−ன் நிலை வெக்டர்களாகும்.
நிரூபணம்
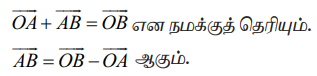
தேற்றம் 8.1 (பிரிவு சூத்திரம்−உட்புறமாகப் பிரித்தல்) (Section Formula − Internal Division)
O−வை ஆதியாகவும். A மற்றும் B−யை ஏதேனும் இரு புள்ளிகளாகவும் கொள்க. மேலும் P என்ற புள்ளியானது ABஎன்ற கோட்டுத்துண்டை m : n என்ற விகிதத்தில் உட்புறமாக பிரிக்கிறது என்க. 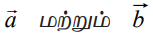 ஆகியவை A மற்றும் B−ன் நிலை வெக்டர்களாயின் P −ன் நிலை வெக்டர்
ஆகியவை A மற்றும் B−ன் நிலை வெக்டர்களாயின் P −ன் நிலை வெக்டர்
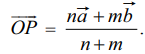
நிரூபணம்
O ஆதிப்புள்ளி மற்றும் A மற்றும் B−ன் நிலை வெக்டர்கள் முறையே 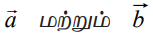 என்பதால்,
என்பதால்,

தேற்றம் 8.2 பிரிவு சூத்திரம்−வெளிப்புறமாகப் பிரித்தல் (நிரூபணமின்றி) (Section Formula − External Division)
O−வை ஆதியாகவும், A மற்றும் B−யை ஏதேனும் இரண்டு புள்ளிகளாகவும் கொள்க. P என்ற புள்ளியானது ABஎன்ற கோட்டுத்துண்டை m : n என்ற விகிதத்தில் வெளிப்புறமாக பிரிக்கிறது என்க. 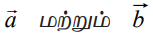 ஆகியவை A மற்றும் B−ன் நிலை வெக்டர்கள் எனில், P−ன் நிலை வெக்டர்
ஆகியவை A மற்றும் B−ன் நிலை வெக்டர்கள் எனில், P−ன் நிலை வெக்டர்
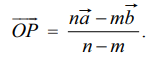
குறிப்பு 8.1
m = n = 1எனத் தேற்றம் 8.1−ல் பிரதியிட A மற்றும் B−யை இணைக்கும் கோட்டின் மையப்புள்ளியின் நிலை வெக்டர் 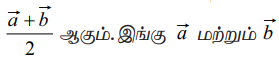 ஆகியவை A மற்றும் B−ன் நிலை வெக்டர்களாகும். மேற்கண்ட தேற்றத்திலிருந்து மூன்று புள்ளிகள் ஒரே நேர்கோட்டில் இருப்பதற்கான கட்டுப்பாட்டைப் பெறலாம்.
ஆகியவை A மற்றும் B−ன் நிலை வெக்டர்களாகும். மேற்கண்ட தேற்றத்திலிருந்து மூன்று புள்ளிகள் ஒரே நேர்கோட்டில் இருப்பதற்கான கட்டுப்பாட்டைப் பெறலாம்.
முடிவு 8.7
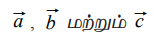 ஆகியவற்றை நிலை வெக்டர்களாக கொண்ட புள்ளிகள் A, Bமற்றும் C ஒரே கோட்டில் அமையத் தேவையான மற்றும் போதுமான நிபந்தனை x, y, z, என்ற மெய்யெண்கள் அனைத்தும் பூஜ்ஜியமில்லாமல் x + y + z = 0 மற்றும்
ஆகியவற்றை நிலை வெக்டர்களாக கொண்ட புள்ளிகள் A, Bமற்றும் C ஒரே கோட்டில் அமையத் தேவையான மற்றும் போதுமான நிபந்தனை x, y, z, என்ற மெய்யெண்கள் அனைத்தும் பூஜ்ஜியமில்லாமல் x + y + z = 0 மற்றும்  என்றவாறு அமைய வேண்டும்.
என்றவாறு அமைய வேண்டும்.
எடுத்துக்காட்டு 8.3
A மற்றும் Bஎன்ற இரு புள்ளிகளின் நிலை வெக்டர்கள் 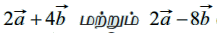 என்க. A மற்றும் B−யை இணைக்கும் கோட்டுத்துண்டினை 1 : 3 என்ற விகிதத்தில் உட்புறமாகவும், வெளிப்புறமாகவும் பிரிக்கும் புள்ளிகளின் நிலை வெக்டர்களைக் காண்க.
என்க. A மற்றும் B−யை இணைக்கும் கோட்டுத்துண்டினை 1 : 3 என்ற விகிதத்தில் உட்புறமாகவும், வெளிப்புறமாகவும் பிரிக்கும் புள்ளிகளின் நிலை வெக்டர்களைக் காண்க.
தீர்வு
O−வை ஆதியாகக் கொள்க.
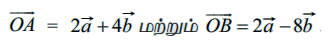 எனக் கொடுக்கப்பட்டுள்ளது.
எனக் கொடுக்கப்பட்டுள்ளது.
C மற்றும் D என்ற புள்ளிகள் ABஎன்ற கோட்டுத்துண்டை 1 : 3 என்ற விகிதத்தில் முறையே உட்புறமாகவும் வெளிப்புறமாகவும் பிரிக்கின்றது என்க.
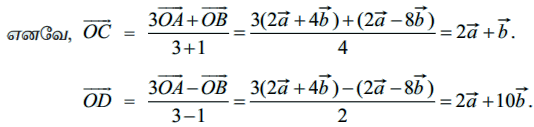
ஒரு முக்கோணத்தின் ஓர் உச்சிப்புள்ளியில் இருந்து அதன் எதிர்ப்பக்கத்தின் மையப்புள்ளியை இணைக்கும் கோடு நடுக்கோடு என்பதை நாம் நினைவு கூர்வோம். மையக்கோட்டுச்சந்தி நடுக்கோட்டினை 2 : 1 என்ற விகிதத்தில் உட்புறமாகப் பிரிக்கும்.
தேற்றம் 8.3
ஒரு முக்கோணத்தின் நடுக்கோடுகள் ஒரு புள்ளியில் சந்திக்கும் என நிறுவுக.
நிரூபணம்
ABC என்ற முக்கோணத்தில் BC, CA மற்றும் ABஆகிய பக்கங்களின் மையப்புள்ளிகள் முறையே D, E, F என்க. நாம் AD, BE, CF ஆகிய நடுக்கோடுகள் ஒரு புள்ளியில் சந்திக்கும் என நிறுவ வேண்டும்.
O−வை ஆதிப்புள்ளியாகக் கொண்டு A, B, C என்ற முனைப்புள்ளிகளின் நிலை வெக்டர்கள் முறையே 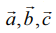 என்க.
என்க.

(1), (2), (3)−லிருந்து G1, G2, G3, ஆகியவற்றின் நிலை வெக்டர்கள் சமம். எனவே அவை வெவ்வேறான புள்ளிகள் இல்லை. அந்த பொதுப்புள்ளியை G என்க.
முக்கோணத்தின் நடுக்கோடுகள் ஒரு புள்ளியின் வழிச் சந்திக்கின்றன.
தேற்றம் 8.4
ஒரு நாற்கரம் இணைகரமாக இருக்கத் தேவையானது மற்றும் போதுமான நிபந்தனை அதன் மூலைவிட்டங்கள் இருசமக் கூறிடும் என்பதாகும்.
நிரூபணம்
AC, BD ஆகியவற்றை மூலைவிட்டங்களாக கொண்ட நாற்கரத்தின் முனைப்புள்ளிகள் A, B, C, D என்க. O−வை ஆதியாகக் கொண்டு A, B, C மற்றும் D−ன் நிலை வெக்டர்கள் 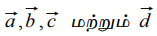 என்க.
என்க.
நாற்கரம் ABCD ஓர் இணைகரம் எனக் கொள்க.
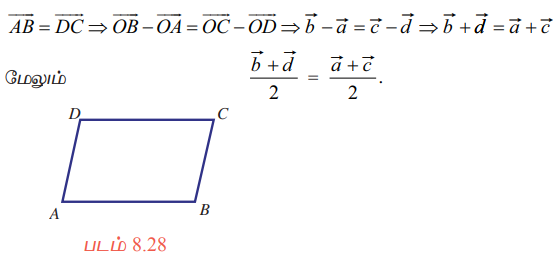
இதிலிருந்து AC மற்றும் BD ஆகியவற்றின் மையப்புள்ளிகளின் நிலை வெக்டர்கள் ஒன்றே ஆகும். அதாவது, மூலைவிட்டங்கள் ஒன்றையொன்று இரு சமக்கூறிடுகின்றன.
மறுதலையாக, நாற்கரத்தின் மூலைவிட்டங்கள் ஒன்றையொன்று இரு சமக்கூறிடுகின்றன எனக் கொண்டால், மூலைவிட்டங்கள் AC மற்றும் BD ஆகியவற்றின் மையப்புள்ளிகளின் நிலை வெக்டர்கள் சமம் ஆகும்.
