11 வது கணக்கு : அலகு 8 : வெக்டர் இயற்கணிதம் (Vector Algebra)
திசையிலிப் பெருக்கம் (Scalar product) திசையிலிப் பெருக்கத்தின் பண்புகள் (Properties of Scalar Product)
திசையிலிப் பெருக்கம் (Scalar product)
வரையறை 8.16
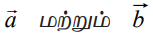 என்ற இரு பூஜ்ஜியமற்ற வெக்டர்களுக்கு இடைப்பட்ட கோணம் θ என்க. (படம் 8.34). இவற்றின் திசையிலிப் பெருக்கம் அல்லது புள்ளிப் பெருக்கம்
என்ற இரு பூஜ்ஜியமற்ற வெக்டர்களுக்கு இடைப்பட்ட கோணம் θ என்க. (படம் 8.34). இவற்றின் திசையிலிப் பெருக்கம் அல்லது புள்ளிப் பெருக்கம் ![]() எனக் குறிக்கப்பட்டு
எனக் குறிக்கப்பட்டு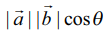 என வரையறுக்கப்படுகிறது.
என வரையறுக்கப்படுகிறது.
அதாவது, ![]() .
.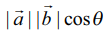
![]() கணக்கிடும்போது கிடைப்பது ஒரு திசையிலி. எனவே இதனைத் திசையிலிப் பெருக்கம் என்கிறோம். மேலும், இவற்றிற்கு இடையே புள்ளி (‘.') என்ற செயலியை பயன்படுத்துவதால் இதனைப் புள்ளிப் பெருக்கம் என்றும் கூறலாம்.
கணக்கிடும்போது கிடைப்பது ஒரு திசையிலி. எனவே இதனைத் திசையிலிப் பெருக்கம் என்கிறோம். மேலும், இவற்றிற்கு இடையே புள்ளி (‘.') என்ற செயலியை பயன்படுத்துவதால் இதனைப் புள்ளிப் பெருக்கம் என்றும் கூறலாம்.
திசையிலிப் பெருக்கத்தின் வடிவக் கணித விளக்கம் (ஒரு வெக்டரின் மீது மற்றொரு வெக்டரின் வீழல்) (Geometrical meaning of scalar product (projection of one vector on another vector))

திசையிலிப் பெருக்கத்தின் பண்புகள் (Properties of Scalar Product)
(i) இரண்டு வெக்டர்களின் திசையிலிப் பெருக்கம் பரிமாற்றுப் பண்புடையது. வழக்கமான வரையறையின்படி 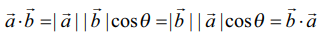 அதாவது, ஏதேனும் இரு வெக்டர்கள்
அதாவது, ஏதேனும் இரு வெக்டர்கள் 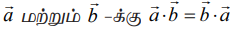
(ii) திசையிலிப் பெருக்கத்தின் தன்மை 0 ≤ θ ≤ π என நமக்குத் தெரியும்.
θ = 0 எனில் ![]() [வெக்டர்கள் இணை மற்றும் ஒரே திசையில் இருக்கும்போது θ = 0].
[வெக்டர்கள் இணை மற்றும் ஒரே திசையில் இருக்கும்போது θ = 0].
θ = π எனில் ![]() [வெக்டர்கள் இணை மற்றும் எதிர்திசையில் இருக்கும்போது θ = π.].
[வெக்டர்கள் இணை மற்றும் எதிர்திசையில் இருக்கும்போது θ = π.].
θ = π/2 எனில் ![]() [இரண்டு வெக்டர்களும் செங்குத்து எனில் θ = π/2].
[இரண்டு வெக்டர்களும் செங்குத்து எனில் θ = π/2].
0 < θ < π/2 எனில், cos θ மிகை. எனவே, ![]() −யும் மிகை.
−யும் மிகை.
π/2 < θ < π எனில் cos θ குறை. எனவே ![]() −யும் குறை.
−யும் குறை.

நிரூபணம்
பண்பு (iii)−ன் படி
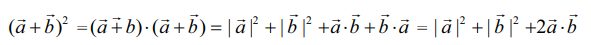
இதே போன்று மற்றவற்றையும் நிறுவலாம்.
(x) திசையிலிப் பெருக்கத்தைக் காணச் செயல் விதி
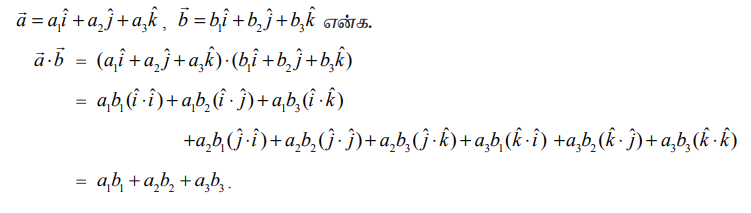
ஆகவே, இரண்டு வெக்டர்களின் திசையிலிப் பெருக்கல் என்பது அவைகளின் ஒத்திசைவான ஆயத்தொலைகளின் குணகங்களைப் பெருக்கிக் கூட்டுவதற்குச் சமம் ஆகும்.

இதில் ஏதேனும் ஒரு வெக்டர் பூஜ்ஜிய வெக்டர் எனில், இவை சமம் ஆகும். எனவே இரண்டு வெக்டர்களும் பூஜ்ஜியமற்ற வெக்டர்கள் என்க.
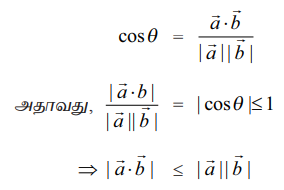
எடுத்துக்காட்டு 8.11

குறிப்பு 8.5
மூன்று பக்கங்கள் வெக்டர் வடிவில் கொடுக்கப்பட்டால், இவை முக்கோணத்தின் பக்கங்களாக இருக்க,
(i) இந்த வெக்டர்களின் கூடுதல் ![]() அல்லது ஏதேனும் இரண்டு வெக்டர்களின் கூடுதல் மூன்றாவது பக்கத்திற்கு சமம் என நிறுவ வேண்டும்.
அல்லது ஏதேனும் இரண்டு வெக்டர்களின் கூடுதல் மூன்றாவது பக்கத்திற்கு சமம் என நிறுவ வேண்டும்.
(ii) செங்கோண முக்கோணத்தில் ஒரு கோணம் π/2 எனக் காட்ட ஏதேனும் இரு வெக்டர்களுக்கு இடைப்பட்ட புள்ளிப் பெருக்கம் 0 என நிரூபிக்க வேண்டும்.