நியூட்டன் விதிகளின் பயன்பாடு : சாய்தளத்தில் இயங்கும் பொருளின் இயக்கம்

சாய்தளத்தில் இயங்கும் பொருளின் இயக்கம் 

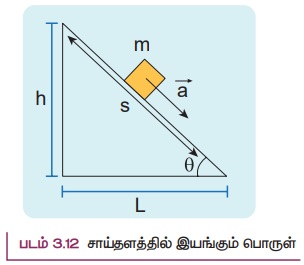
m நிறையுடைய பொருள் ஒன்று, சாய் கோணம் θ கொண்ட உராய்வற்ற சாய்தளம் ஒன்றில் படம் 3.12 இல் காட்டியுள்ளவாறு சறுக்கிச் செல்கிறது என்க. அப்பொருளின் மீது செயல்படும் விசைகள் பின்வருவனவற்றைத் தீர்மானிக்கின்றன. 

(a) பொருளின் முடுக்கம் 

(b) பொருள் தரையை அடையும்போது அதன் வேகம் 

பொருளின் மீது செயல்படும் விசைகள் 

(i) கீழ்நோக்கிச் செயல்படும் புவியீர்ப்பு விசை (mg)

(ii) சாய்தளத்திற்குச் செங்குத்தாகப் பொருளின்மீது செயல்படும் செங்குத்து விசை (N)

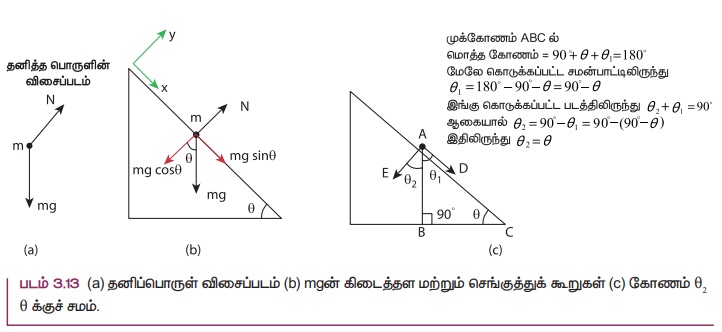
பொருளின் தனிப் பொருள் விசைப்படம் வரைய, அப்பொருளை ஒரு புள்ளிநிறையாகக் கருத வேண்டும். 

(படம் 3.13 (a)) இல் காட்டியுள்ளபடி இயக்கம் சாய்தளத்தில் நடைபெறுவதால் படம் 3.13 (b) இல் காட்டியவாறு சாய்தளத்திற்கு இணையாக உள்ள ஒரு ஆய அச்சு அமைப்பினை தேர்வு செய்ய வேண்டும். 

புவியீர்ப்பு விசை mg ஐ இரண்டு கூறுகளாகப் பிரிக்க வேண்டும் 

mg sinθ கூறு சாய்தளத்திற்கு இணையாகவும், mg cosθ கூறு சாய்தளத்திற்கு செங்குத்தாகவும் உள்நோக்கி செயல்படுகின்றன. (படம் 3.13 (b)). 

புவியீர்ப்பு விசை (mg) சாய்தளத்தின் கீழ்நோக்கிய செங்குத்துடன் ஏற்படுத்தும் கோணம், படம் 3.13 (c)) இல் காட்டப்பட்டுள்ள சாய் கோணம் (θ)விற்குச் சமம். 

y அச்சுத்திசையில் எவ்விதமான இயக்கமும் முடுக்கமும் இல்லை. 

y அச்சுத்திசையில் நியூட்டனின் இரண்டாம் விதியைப் பயன்படுத்தினால்

சமன்பாட்டின் இருபுறமும் உள்ள கூறுகளை ஒப்பிடும் போது N − mg cosθ = 0

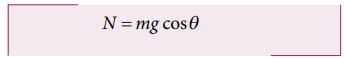
சாய்தளப்பரப்பு ஏற்படுத்தும் செங்குத்து விசையின் (N) எண்மதிப்பு mg cosθ விற்குச் சமம்.

பொருள் x அச்சுத்திசையில் a முடுக்கத்துடன் சறுக்கிச் செல்கிறது. எனவே x அச்சுத்திசையில் நியுட்டன் இரண்டாம் விதியை பயன்படுத்தினால்

இங்கு பொருளின் முடுக்கம், சாய்கோணம் θ வைச் சார்ந்தது என்பதை கவனிக்க வேண்டும். சாய்கோணம் θ = 90° எனில் பொருள் (a = g) என்ற முடுக்கத்துடன் செங்குத்தாக கீழ்நோக்கி வரும். 

பொருள் தரையை அடையும்போது அதன் வேகத்தை நியூட்டனின் இயக்கச் சமன்பாடுகள் கொண்டு அறியலாம். இயக்கம் முழுமைக்கும் முடுக்கம் ஒரு மாறிலி ஆகும்.

முடுக்கம் a = gsin θ க்குச் சமம். பொருள் ஓய்வு நிலையிலிருந்து நகரத்துவங்கும்போது ஆரம்பத் திசைவேகம் u சுழியாகும். மேலும் சாய்தளத்தின் நீளம் இங்கு s ஆகும்.

சமன்பாடு (3.3) லிருந்து தரையை அடையும் போது பொருளின் வேகம் (v)

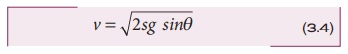
இங்கு நாம் சாய்தளத்திற்கு இணையாக ஆய அச்சுத் தொகுப்பினை தேர்வு செய்தோம். மாறாக சமதளப்பரப்பிற்கு இணையாக ஆயக் கூறுகளை தேர்வு செய்தாலும் இதே முடிவுகள் தான் கிடைக்கும். இருப்பினும் கணிதமுறை சற்றே கடினமாக இருக்கும். எனவே கொடுக்கப்பட்ட வினாவிற்கு ஏற்ப ஆயக்கூறுகளை தேர்வு செய்வது சாலச்சிறந்ததாகும்.