11வது இயற்பியல் : அலகு 3 : இயக்க விதிகள்
மொத்த நேர்க்கோட்டு உந்த மாறா விதி
மொத்த நேர்க்கோட்டு உந்த மாறா விதி
மாறா விதிகள் (conservation laws) இயற்கையில் ஒரு முக்கியமான அங்கத்தை வகிக்கிறது. மாறா விதிகளைப்பயன்படுத்தி இயங்கும் பொருட்களின் இயக்கங்களை சிறப்பாக பகுப்பாய்வு செய்ய இயலும். இயங்கியலில் அல்லது எந்திரவியலில் மூன்று மாறா விதிகள் உள்ளன. அவை பின்வருமாறு
(i) ஆற்றல் மாறா விதி (law of conservation of energy)
(ii) மொத்த நேர்க்கோட்டு உந்த மாறா விதி (law of conservation of total linear momentum.) மற்றும் கோண உந்த மாறா விதி (law of conservation of angular momentum.)
நியூட்டனின் இரண்டாம் விதி மற்றும் மூன்றாம் விதிகளை ஒன்றிணைத்து, மொத்த நேர்க்கோட்டு உந்த மாறா விதியைப் பெறலாம்.
இரண்டு துகள்கள், ஒன்றோடொன்று தொடர்பு கொள்ளும் போது, ஒரு துகள் செயல் எதிர்செயல் புரியும்போது ஒவ்வொரு துகளும் மற்ற துகளின் மீது ![]() என்ற விசையை செலுத்தினால், அதே நேரத்தில் இரண்டாவது துகள், முதல் துகளின்மீது
என்ற விசையை செலுத்தினால், அதே நேரத்தில் இரண்டாவது துகள், முதல் துகளின்மீது ![]() என்ற சமமான எதிர்விசையைச் செலுத்தும். எனவே நியூட்டனின் மூன்றாம் விதிப்படி
என்ற சமமான எதிர்விசையைச் செலுத்தும். எனவே நியூட்டனின் மூன்றாம் விதிப்படி
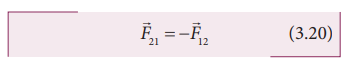
துகள்களின் உந்தங்கள் அடிப்படையில் ஒவ்வொரு
துகள் மீதும் செயல்படும் விசையை நியூட்டன் இரண்டாம் விதியினைக் கொண்டு கணக்கிடலாம்.
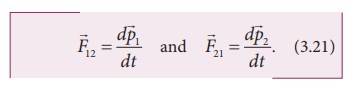
இங்கு ![]() என்பது முதல் துகளின் உந்தம், அது இரண்டாம்
துகள் செலுத்தும்
என்பது முதல் துகளின் உந்தம், அது இரண்டாம்
துகள் செலுத்தும் ![]() என்ற விசையினால் மாற்றமடைகிறது. அதே போல
என்ற விசையினால் மாற்றமடைகிறது. அதே போல ![]() என்பது இரண்டாம் துகளின் உந்தம். இவ்வுந்தமானது முதல் துகள் இரண்டாவது துகளின் மீது செலுத்தும்
என்பது இரண்டாம் துகளின் உந்தம். இவ்வுந்தமானது முதல் துகள் இரண்டாவது துகளின் மீது செலுத்தும் ![]() என்ற விசையினால் மாற்றமடைகிறது.
என்ற விசையினால் மாற்றமடைகிறது.
(சமன்பாடு 3.21) சமன்பாடு (3.20) இல் பிரதியிடுக.
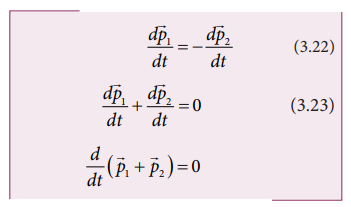
இதிலிருந்து ![]() +
+ ![]() எப்பொழுதும் மாறா வெக்டர் என்பதை அறியலாம்.
எப்பொழுதும் மாறா வெக்டர் என்பதை அறியலாம்.
இங்கு ![]() +
+ ![]() என்பது இரண்டு துகள்களின் மொத்த நேர்க்கோட்டு உந்தமாகும்.
என்பது இரண்டு துகள்களின் மொத்த நேர்க்கோட்டு உந்தமாகும்.
(![]() =
= ![]() +
+ ![]() ) இதை அமைப்பின் மொத்த நேர்க்கோட்டு உந்தம் என்றும் அழைக்கலாம். இம்முடிவிலிருந்து மொத்த நேர்க்கோட்டு உந்த மாறா விதியை பின்வருமாறு வரையறை செய்யலாம்.
) இதை அமைப்பின் மொத்த நேர்க்கோட்டு உந்தம் என்றும் அழைக்கலாம். இம்முடிவிலிருந்து மொத்த நேர்க்கோட்டு உந்த மாறா விதியை பின்வருமாறு வரையறை செய்யலாம்.
அமைப்பின் மீது எவ்வித வெளிப்புற விசையும் செயல்படாத நிலையில், அமைப்பின் மொத்த நேர்க்கோட்டு உந்தம் எப்பொழுதும் ஒரு மாறா வெக்டராகும். வேறு வகையில் கூறுவோமாயின் அமைப்பின் மொத்த நேர்க்கோட்டு உந்தம் நேரத்தைப் பொருத்து மாறாது.
இங்கு ![]() மற்றும்
மற்றும் ![]() வில் ஏதேனும் மாற்றம் ஏற்பட்டாலும் அமைப்பின் மொத்தநேர்க்கோட்டு உந்தம்
வில் ஏதேனும் மாற்றம் ஏற்பட்டாலும் அமைப்பின் மொத்தநேர்க்கோட்டு உந்தம் ![]() +
+ ![]() மாறாது என்பதைப் புரிந்துகொள்ள வேண்டும்.
மாறாது என்பதைப் புரிந்துகொள்ள வேண்டும். ![]() மற்றும்
மற்றும் ![]() விசைகளை அமைப்பின் அகவிசைகள் என்று அழைக்கலாம். ஏனெனில் இவ்விசைகள் துகள்களுக்கிடையே மட்டும் செயல்படுகின்றன. துகளின் மீது எவ்வித வெளிப்புற விசையும் செயல்படாத நிலையில் அமைப்பின் மொத்த நேர்க்கோட்டு உந்தம் ஒரு மாறா வெக்டராகும்.
விசைகளை அமைப்பின் அகவிசைகள் என்று அழைக்கலாம். ஏனெனில் இவ்விசைகள் துகள்களுக்கிடையே மட்டும் செயல்படுகின்றன. துகளின் மீது எவ்வித வெளிப்புற விசையும் செயல்படாத நிலையில் அமைப்பின் மொத்த நேர்க்கோட்டு உந்தம் ஒரு மாறா வெக்டராகும்.
எடுத்துக்காட்டு 3.15
கீழ்க்கண்ட அமைப்புகளில் செயல்படும் அக மற்றும் புற விசைகளை காண்க.
a) புவியை மட்டும் தனியாகக் கொண்ட அமைப்பு
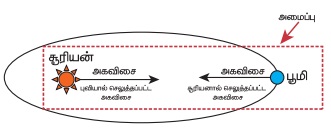
b) புவி மற்றும் சூரியன் இணைந்த அமைப்பு
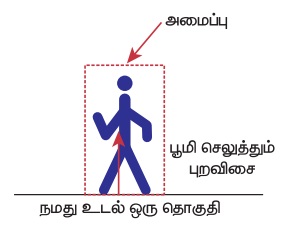
c) நடக்கும் மனிதன் - என்ற அமைப்பு
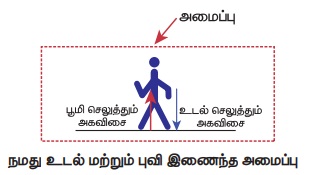
d) நமது உடல் மற்றும் புவி இணைந்த அமைப்பு
தீர்வு
(a) புவி மட்டும் கொண்ட அமைப்பு
சூரியனின் ஈர்ப்பு விசையினால், புவி சூரியனைச் சுற்றிவருகிறது. புவியினைத் தனித்த அமைப்பு எனக்கருதினால், சூரியனின் ஈர்ப்பு விசையை புறவிசையாகக் கருதலாம். நிலவையும் நாம் கணக்கில் எடுத்துக்கொண்டால், நிலவும் புவியின் மீது ஒரு புறவிசையைச் செலுத்தும்.
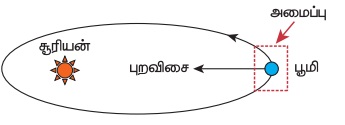
(b) புவி மற்றும் சூரியன் இணைந்த அமைப்பு
இந்நேர்வில், இரண்டு அக விசைகள் செயல் - எதிர்ச்செயல் விசை சோடியாக செயல்படுகின்றன. ஒன்று சூரியன் புவியின் மீது செலுத்தும் ஈர்ப்பு விசை, மற்றொன்று புவி சூரியனின் மீது செலுத்தும் ஈர்ப்புவிசை ஆகும்.
(c) நடக்கும் மனிதன் - என்ற அமைப்பு
நடக்கும் போது, நாம் புவியின் மீது ஒரு விசையை செலுத்தும் அதே நேரத்தில் புவியும் இதற்குச்சமமான எதிர்விசை ஒன்றை நம்மீது செலுத்துகிறது. நமது உடலை மட்டும் ஒரு அமைப்பாகக் கருதினால் புவி நம்மீது செலுத்தும் எதிர்விசையை புறவிசை எனக்கருதலாம்.
(d) நமது உடல் மற்றும் புவி இணைந்த அமைப்பு
இந்நிகழ்வில், இரண்டு அக விசைகள் அமைப்பில் உள்ளன. ஒன்று நாம் புவியின் மீது செலுத்தும் விசை, மற்றொன்று புவி நம்மீது செலுத்தும் சமமான எதிர்விசை.
உந்த மாறா விதியின் பொருள்
1) உந்த மாறா விதி ஒரு வெக்டர் விதியாகும். இவ்விதி மொத்த நேர்க்கோட்டு உந்தத்தின் எண் மதிப்பு மற்றும் திசை மாறாதவை எனக்காட்டுகிறது. சில நேர்வுகளில் மொத்த நேர்க்கோட்டு உந்தம் சுழி மதிப்பையும் பெறலாம்.
2) பொருளொன்றின் இயக்கத்தினைப் பகுப்பாய்வு செய்யும்போது நியூட்டனின் இரண்டாம் விதி அல்லது நேர்க்கோட்டு உந்த மாறா விதியை நாம் பயன்படுத்தலாம். நியூட்டனின் இரண்டாவது விதியைப் பயன்படுத்த வேண்டுமானால் நாம் பொருளின் மீது செயல்படும் விசைகளைக் குறிப்பிட வேண்டும். நடைமுறைச் சூழலில் இது கடினமாகும். ஆனால் உந்த மாறா விதியில், இவ்வாறு விசைகளைச் சுட்டிக்காட்ட வேண்டிய அவசியமில்லை. எனவே உந்த மாறா விதி பயன்படுத்துவதற்கு எளிமையானது மற்றும் முக்கியத்துவம் வாய்ந்ததாகும்.
எடுத்துக்காட்டாக, இரண்டு பொருட்கள் ஒன்றுடன் ஒன்று மோதும் நிகழ்வில் அவ்விரண்டு பொருட்களும் ஒன்றின்மீது மற்றொன்று செலுத்தும் விசையைக் குறிப்பிடுவது சற்றே கடினமாகும். ஆனால் மோதலின்போது உந்த மாறா விதியை பயன்படுத்துவது எளிமையாகும்.
எடுத்துக்காட்டுகள்
(1) துப்பாக்கி சுடும் நிகழ்வு ஒன்றைக் கருதுக. இங்கு துப்பாக்கி மற்றும் குண்டு இரண்டும் சேர்ந்தது ஒரு அமைப்பு ஆகும். தொடக்கத்தில் துப்பாக்கி மற்றும் குண்டு இரண்டும் ஓய்வு நிலையில் உள்ளன எனவே அமைப்பின் மொத்த நேர்க்கோட்டு உந்தம் சுழியாகும். ![]() என்பது குண்டின் உந்தமாகவும்,
என்பது குண்டின் உந்தமாகவும், ![]() என்பது துப்பாக்கியின் உந்தமாகவும் கருதுக. இங்கு இரண்டும் ஓய்வு நிலையில் உள்ளன.
என்பது துப்பாக்கியின் உந்தமாகவும் கருதுக. இங்கு இரண்டும் ஓய்வு நிலையில் உள்ளன.
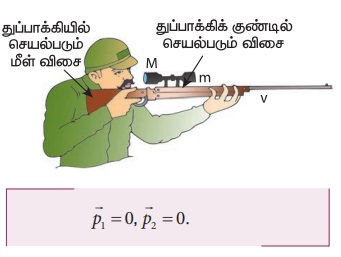
சுடுவதற்கு முன் மொத்த உந்தம் சுழி  நேர்க்கோட்டு உந்த அழிவின்மை விதிப்படி, துப்பாக்கி சுட்ட பின்பும் மொத்த நேர்க்கோட்டு உந்தம் சுழி மதிப்பைப் பெற வேண்டும்.
நேர்க்கோட்டு உந்த அழிவின்மை விதிப்படி, துப்பாக்கி சுட்ட பின்பும் மொத்த நேர்க்கோட்டு உந்தம் சுழி மதிப்பைப் பெற வேண்டும்.
துப்பாக்கி சுடப்படும்போது, துப்பாக்கி முன்னோக்கிய திசையில் ஒரு விசையை குண்டின் மீது செலுத்தும். எனவே குண்டின் உந்தம் 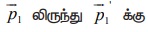 மாற்றமடையும். நேர்க்கோடு உந்த மாறா விதியின் காரணமாக துப்பாக்கியின் உந்தமும்
மாற்றமடையும். நேர்க்கோடு உந்த மாறா விதியின் காரணமாக துப்பாக்கியின் உந்தமும் ![]() விலிருந்து
விலிருந்து ![]() மாற்றமடையும். உந்த மாறா விதிப்படி
மாற்றமடையும். உந்த மாறா விதிப்படி 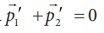 இதிலிருந்து
இதிலிருந்து 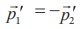 என அறியலாம். எனவே துப்பாக்கியின் உந்தம் துப்பாக்கிக் குண்டின் உந்தத்திற்கு எதிர்திசையில் இருக்கும்.
என அறியலாம். எனவே துப்பாக்கியின் உந்தம் துப்பாக்கிக் குண்டின் உந்தத்திற்கு எதிர்திசையில் இருக்கும்.
இதன் காரணமாகத்தான் துப்பாக்கி சுடப்பட்ட பின்பு, ![]() என்ற ஒரு உந்தத்துடன் பின்னோக்கி இயங்கும். இதற்கு ‘பின்னியக்க உந்தம்’ என்று பெயர். இந்த இயக்கம் உந்த மாறா விதிக்கு ஒரு எடுத்துக் காட்டு ஆகும்.
என்ற ஒரு உந்தத்துடன் பின்னோக்கி இயங்கும். இதற்கு ‘பின்னியக்க உந்தம்’ என்று பெயர். இந்த இயக்கம் உந்த மாறா விதிக்கு ஒரு எடுத்துக் காட்டு ஆகும்.
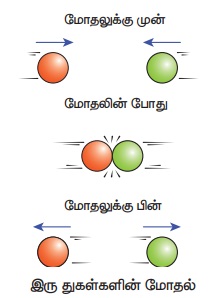
(2) ஓய்வு நிலையிலுள்ள ஒரு பொருள், மற்றும் அதை நோக்கிய திசையில் இயங்கும் பொருள் ஆகிய இரண்டு பொருட்களைக் கருதுக. இவை இரண்டும் ஒன்றுடன் ஒன்று மோதி, மோதலுக்குப்பின் தன்னிச்சையான திசையில் செல்கின்றன.
இந்நிகழ்வில், மோதலுக்கு முன்பு அமைப்பின் மொத்த நேர்க்கோட்டு உந்தம், இயக்கத்திலுள்ள பொருட்களின் தொடக்க நேர்க்கோட்டு உந்தத்திற்குச் சமமாகும். நேர்க்கோட்டு உந்த மாறா விதிப்படி, மோதலுக்கு பின்பும் அமைப்பின் மொத்த நேர்க்கோட்டு உந்தம் முன்னோக்கிய திசையில் செயல்படும். பின்வரும் படம் இதனை விளக்குகிறது.
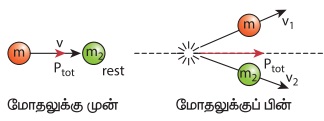
மோதலுக்கு முன்பு
பிரிவு 4.4 இல் இம்மோதல் பற்றிய விரிவான கணக்கீடுகள் வழங்கப்பட்டுள்ளன. இங்கு பின்வரும் கருத்தைப் புரிந்து கொள்வது பயனுள்ளதாக இருக்கும். மோதலுக்கு முன்பும், பின்பும் மொத்த உந்த வெக்டர் ஒரே திசையில் உள்ளது. இது மொத்த நேர்க்கோட்டு உந்தம் மோதலுக்கு முன்பும் பின்பும் ஒரு மாறிலி வெக்டர் என்பதை எளிமையாக விளக்குகின்றது. மோதலின்போது ஒவ்வொரு பொருளும் மற்ற பொருளின் மீது ஒரு விசையைச் செலுத்தும். இவ்விரண்டு பொருட்களையும் ஒரு அமைப்பு எனக் கருதினால், இவ்விரண்டு விசைகளும் அகவிசைகளாகும். எனவே இந்த அகவிசைகள் மொத்த நேர்க்கோட்டு உந்தத்தை மாற்றாது.
கணத்தாக்கு
மிக அதிக விசை, மிகக்குறுகிய நேரத்திற்கு ஒரு பொருளின் மீது செயல்பட்டால் அவ்விசையை கணத்தாக்கு விசை அல்லது கணத்தாக்கு என்று அழைக்கலாம்.
F என்ற விசை, மிகக் குறுகிய நேர இடைவெளியில் (Δt) ஒரு பொருளின் மீது செயல்பட்டால் நியூட்டன் இரண்டாம் விதியின் எண் மதிப்பு வடிவில் இந்நிகழ்வினை பின்வருமாறு குறிப்பிடலாம்.
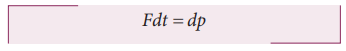
தொடக்க நேரம் t i மற்றும் இறுதி நேரம் tf என்ற கால இடைவெளியில் இச்சமன்பாட்டை தொகையிட

pf - pi = ∆p என்பது tf - ti = ∆t என்ற நேர இடைவெளியில் பொருளில் ஏற்பட்ட உந்த மாற்றமாகும். தொகையீடு 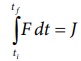 என்பது கணத்தாக்கு எனப்படும். மேலும், இக்கணத்தாக்கு பொருளின் உந்த மாற்றத்திற்கு சமமாகும்.
என்பது கணத்தாக்கு எனப்படும். மேலும், இக்கணத்தாக்கு பொருளின் உந்த மாற்றத்திற்கு சமமாகும்.
கொடுக்கப்பட்ட நேர இடைவெளியில் விசை ஒரு மாறா மதிப்பைப் பெற்றிருப்பின்
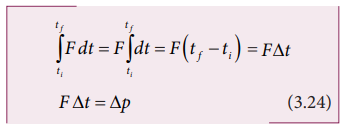
சமன்பாடு (3.24) க்கு “கணத்தாக்கு - உந்தச் சமன்பாடு” என்று பெயர்.
விசை ஒரு மாறா மதிப்பைப் பெற்றுள்ளபோது, கணத்தாக்கு J = F Δt எனக் குறிப்பிடப்படுகிறது. மேலும், இது Δt என்ற நேர இடைவெளியில் பொருளில் ஏற்படும் உந்த மாற்றத்திற்கு ( Δp) சமம் ஆகும்.

ஒரு சிறிய நேர இடைவெளியில் பொருளின் மீது செயல்படும் சராசரி விசையைப் பின்வருமாறு வரையறை செய்யலாம்.
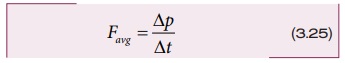
சமன்பாடு (3.25) லிருந்து, நேர இடைவெளி மிகக் குறுகியதாக இருப்பின், பொருளின்மீது செயல்படும் சராசரி விசை மிக அதிகமாக இருக்கும். பொருளின் உந்தம் எப்பொழுதெல்லாம் மிகவேகமாக மாற்றமடைகிறதோ, அப்பொழுதெல்லாம் சராசரி விசை மிக அதிகமாக இருக்கும்.
கணத்தாக்கை, சராசரி விசையின் அடிப்படையிலும் எழுதலாம். ஏனெனில் பொருளின் உந்த மாற்றம் ∆p கணத்தாக்கு (J) க்கு சமமாகும். எனவே
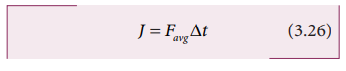
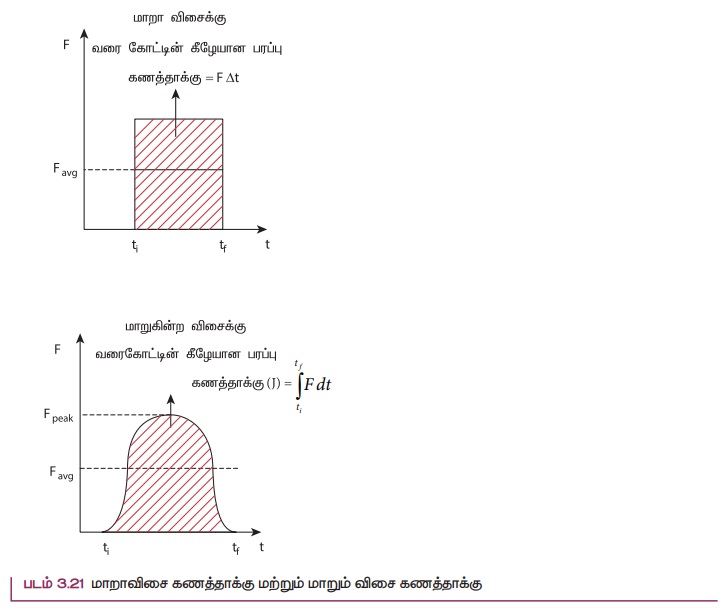
மாறா விசையினால்
ஏற்படும் கணத்தாக்கு மற்றும் மாறும் விசையினால் ஏற்படும் கணத்தாக்கு ஆகியவற்றின் வரைபடம்
படம் 3.21 இல் கொடுக்கப்பட்டுள்ளது.
எடுத்துக்காட்டுகள்
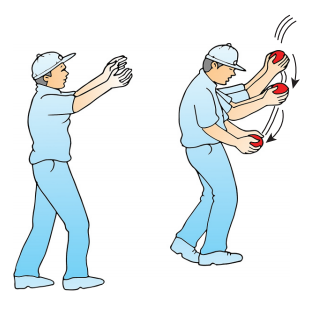
1. கிரிக்கெட் வீரர், வேகமாகவரும் பந்தினை பிடிக்கும்போது அவரின் கரங்களை பந்து வரும் திசையிலேயே படிப்படியாக தாழ்த்துவதன் காரணம் என்ன?
கிரிக்கெட் வீரர் பந்தைப் பிடித்த உடன் தன்னுடைய கரங்களை தாழ்த்தாமல் உடனடியாக நிறுத்தினால் பந்து உடனடியாக ஓய்வுநிலைக்கு வரும். அதாவது பந்தின் உந்தம் உடனடியாக சுழியாகிறது. இதனால் கரங்களின் மீது பந்து செலுத்தும் சராசரி விசை பெரும மதிப்பைப் பெறும். எனவே கிரிக்கெட் வீரரின் கரங்கள் வேகமாக தாக்கப்பட்டு அவர் அதிக வலியினை உணர்வார். இதனைத் தவிர்ப்பதற்காகத்தான் அவர் தன்னுடைய கரங்களை படிப்படியாக தாழ்த்துகிறார்.
2. வேகமாகச் செல்லும் கார் ஒன்று விபத்திற்குள்ளாகும்போது அதன் உந்தம்
மிகக்குறைந்த நேரத்தில் மிக வேகமாகக் குறைகிறது. இது பயணிகளுக்கு பேராபத்தை
விளைவிக்கும். ஏனெனில் பயணிகளின் மீது இவ்வுந்த மாற்றம் பெரும விசையினைச்
செலுத்தும். மரணத்தை ஏற்படுத்தும் இந்த விளைவிலிருந்து பயணிகளைக் காக்க
காற்றுப்பைகளுடன் கார்கள் தற்போது வடிவமைக்கப்படுகின்றன. இந்தக் காற்றுப்பைகள்
பயணிகளின் உந்த மாற்றக் காலத்தை நீட்டித்து அவர்கள் பெரும்
விசையைப்பெறுவதிலிருந்து தடுக்கிறது.

3. இரு சக்கர வாகனங்களில் பொருத்தப்பட்டுள்ள அதிர்வுத்தாங்கிகள் (Shock absorbers):
கார்களில் உள்ள காற்றுப்பைகள் போன்றே இவையும் அதிர்வுதாங்கிகளாக செயலாற்றுகின்றன. மேடுபள்ளங்களில் வாகனம் செல்லும் போது ஒரு திடீர் விசையானது உடனடியாக வாகனத்தின் மீது செலுத்தப்படுகிறது. இவ்விசை பயணிகளை உடனடியாகத் தாக்காமல் அதன் தாக்குதல் நேரத்தை நீட்டிக்க அதிர்வுத்தாங்கிகள் பயன்படுகின்றன. எனவே பயணிகள் பெரும விசையை உணர்வதிலிருந்து தடுக்கப்படுகின்றனர். அதிர்வுத்தாங்கிகள் சரிவர இயங்காத வாகனங்களில் பயணம் செய்வது நமது உடலை பாதிக்கும்.
4. மணல் நிரப்பிய தரையில் குதிப்பதைவிட, கான்கிரீட் தரையில் குதிப்பது பேராபத்தை விளைவிக்கும். ஏனெனில், மணல் நிரப்பப்பட்ட தரை நமது உடல் ஓய்வு நிலையை அடையும் நேரத்தை நீடித்து உடல் பெரும விசையைப் பெறுவதிலிருந்து தடுக்கும். ஆனால் கான்கிரீட் தளத்தில் குதிக்கும் போது உடல் உடனடியாக ஓய்வு நிலைக்கு வந்து ஒரு பெரும விசையை உணரும். இது பேராபத்தை விளைவிக்கும்.

எடுத்துக்காட்டு 3.16
15m s-1 வேகத்தில் இயங்கும் 10 kg நிறையுடைய பொருள் சுவர் மீது மோதி
அ) 0.03 s
ஆ) 10 s ஆகிய நேர இடைவெளிகளில் ஓய்வுநிலையை அடைகிறது. இவ்விரண்டு நேர இடைவெளிகளிலும் பொருளின் கணத்தாக்கு மற்றும் பொருளின் மீது செயல்படும் சராசரி விசை ஆகியவற்றைக் காண்க.
தீர்வு
பொருளின் ஆரம்ப உந்தம்

இரண்டு நேர்வுகளிலும் பொருளின் கணத்தாக்கு சமம். ஆனால் பொருளின் மீது செயல்படும சராசரி விசை வெவ்வேறானவை.