நியூட்டன் விதிகளின் பயன்பாடு : சமதளப்பரப்பில் ஒன்றை ஒன்று தொட்டுக் கொண்டிருக்கும் இரண்டு பொருட்கள்:

சமதளப்பரப்பில் ஒன்றை ஒன்று தொட்டுக் கொண்டிருக்கும் இரண்டு பொருட்கள்: 

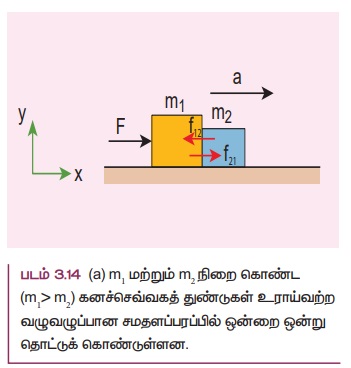
m1 மற்றும் m2 நிறை கொண்ட இரண்டு கனச் செவ்வகத்துண்டுகளைக் கருதுக (m1 > m2) அவை இரண்டும் உராய்வற்ற, வழுவழுப்பான சமதளப்பரப்பில் ஒன்றை ஒன்று தொட்டுக்கொண்டு உள்ளன. (படம் 3.14 (a)) 

F என்ற கிடைத்தள விசையைச் செலுத்தும்போது இவ்விரண்டு துண்டுகளும் a என்ற முடுக்கத்துடன் விசையின் திசையிலேயே இயங்குகின்றன.

முடுக்கம்   ஐ கண்டறிய நியூட்டனின் இரண்டாம் விதியைப் பயன்படுத்த வேண்டும். 

(கூட்டு நிறை m = m1 + m2)

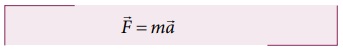
இரு நிறைகள் கொண்ட இவ்வமைப்பு நேர்க்குறி x அச்சு திசையில் இயங்கினால் சமன்பாட்டினை வெக்டர் கூறு வடிவில் எழுதலாம். 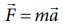என்ற சமன்பாட்டின் இரண்டு பக்கங்களிலும் வெக்டர் கூறுகளை ஒப்பிட F = ma என கிடைக்கும். 

இங்கு m = m1 + m2 ஆகும்.

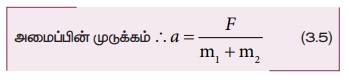
நிறை m1 தனது இயக்கத்தின் காரணமாக, நிறை m2 வின் மீது செலுத்தும் விசை தொடு விசை (contact force) எனப்படும். நியூட்டனின் மூன்றாம் விதிப்படி, நிறை m2 நிறை m1 மீது இதற்குச் சமமான எதிர்திசையில் அமைந்த ஒரு எதிர்விசையை   செலுத்தும். 

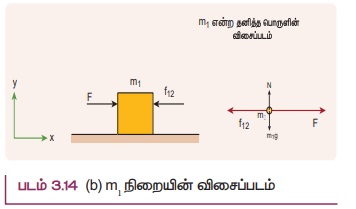
m1 நிறைக்கான விசைப்படம் படம் 3.14 (b) ல் காட்டப்பட்டுள்ளது.

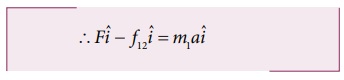
சமன்பாட்டின் இருபுறமும் கூறுகளை ஒப்பிடும்போது

சமன்பாடு (3.7) லிருந்து f12 வின் எண்மதிப்பு எதிர்விசையை ஏற்படுத்தும் நிறை m2 வை சார்ந்திருப்பதை அறியலாம். இங்கு விசை எதிர்குறி x - அச்சுத்திசையில் செயல்ப டுவதை நினைவில் கொள்ளவும். m1 மீது செயல்படும் எதிர்விசை வெக்டர் குறியீட்டின்படி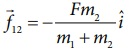

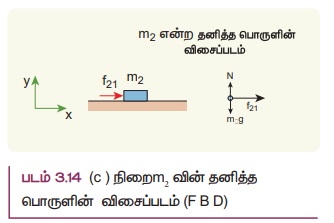
நிறை m2 வைப் பொருத்த வரை x அச்சுத்திசையில் அதன்மீது m1 நிறை ஏற்படுத்தும் ஒரே ஒரு விசை மட்டுமே கிடைத்தளத்திசையில் செயல்படுகிறது. 3.14 (c) ல் நிறை m2 வின் விசைப்படம் காட்டப்பட்டுள்ளது. நிறை m2 விற்கு நியூட்டன் இரண்டாம் விதியைப் பயன்படுத்தினால் f21iˆ = m2aiˆ

சமன்பாட்டின் இருபுறமும் கூறுகளை ஒப்பிடும்போது

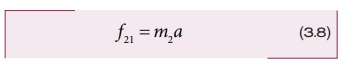
சமன்பாடு (3.5) லிருந்து முடுக்கத்தினை (3.8) ல் பிரதியிடும்போது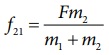

எனவே, தொடுவிசையின் எண் மதிப்பு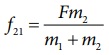 

இது நேர்க்குறி x அச்சுத்திசையில் செயல்படும் 

வெக்டர் குறியீட்டின்படி நிறை m1, நிறை m2 மீது செலுத்தும் விசை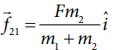

இங்கு 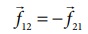என்பதைக் கவனிக்க. இது நியூட்டனின் மூன்றாம் விதியை உறுதிப்படுத்துகிறது.