செவ்வக மற்றும் சதுரத்தின் பரப்பளவு

செவ்வக மற்றும் சதுரத்தின் பரப்பளவு

சூழ்நிலை

கவிதாவின் வீட்டில் அதிகமான கொசுக்கள் உள்ளன. அவை சன்னல் வழியே வீட்டிற்குள் நுழைகின்றன. எனவே, கவிதாவின் அம்மா சன்னல்களுக்குக் கம்பிவலைப் பொருத்த முடிவு செய்தாள். கவிதாவின் அம்மா சன்னலுக்குக் கம்பிவலைப் பொருத்துவதற்கு எவ்வகையான அளவீடு தேவைப்படுகிறது?

சன்னலுக்குக் கம்பிவலை பொருத்துவதற்குத் தேவையான அளவீடு பரப்பளவு ஆகும். 

ஒரு பொருளானது ஒரு சமதளப்பகுதியில் அடைக்கும் இடத்தின் அளவே பரப்பளவு என வரையறை செய்யலாம்.

ஒரு பொருளின் பரப்பளவானது சதுர அலகுகளால் குறிக்கப்படுகிறது. எ.கா 16 சதுர செ.மீ, 24 சதுர செ.மீ.

செவ்வகத்தின் பரப்பளவு காணும் வாய்பாடு

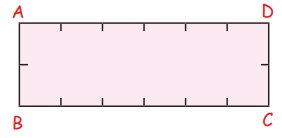
மேலே கொடுக்கப்பட்டுள்ள செவ்வகம் ABCD இல், ஒவ்வொரு பக்கமும் 1 செ.மீ அலகுளகாப் பிரிக்கப்பட்டுள்ளது.

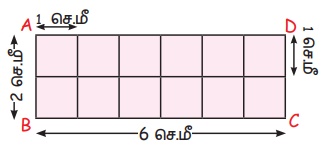
எதிரெதிர் பக்கங்களின் மீதுள்ளப் புள்ளிகள் மேலேயுள்ள படத்தில் காட்டியுள்ளவாறு இணைக்கப்பட்டுள்ளன. இவ்வாறு உருவாக்கப்பட்ட  ஒவ்வொரு சதுரமும் 1 செ.மீ பக்க அளவைக் கொண்டிருக்கும்.

எனவே, ஒவ்வொரு சதுரத்தின் பரப்பளவும் 1 சதுர செ.மீ ஆகும். இது அலகு சதுரம் எனப்படுகிறது.

செவ்வகம் ABCD இல் ஒவ்வொன்றிலும் 6 சதுரங்கள் உள்ளவாறு 2 வரிசைகள் உருவாக்கப்பட்டுள்ளன.

எனவே, செவ்வகம் ABCD இல் உள்ள அலகு சதுரங்களின் எண்ணிக்கை 6 × 2 = 12 ஆகும்.

இங்கு, செவ்வகம் ABCD இன் நீளம் 6 செ.மீ மற்றும் அதன் அகலம் 2 செ.மீ ஆகும்.

உருவாக்கப்பட்ட அலகு சதுரங்களின் எண்ணிக்கை செவ்வகத்தின் நீளம் மற்றும் அகலத்தின் பெருக்கலுக்கு சமம்

எனவே, செவ்வகத்தின் பரப்பளவு ABCD = 6 × 2 = 12 சதுர செ.மீ.

எனவே, செவ்வகத்தின் பரப்பளவு = நீளம் × அகலம்

சதுரத்தின் பரப்பளவு காணும் வாய்பாடு :

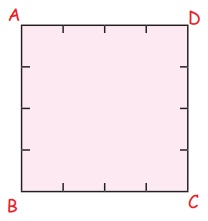
மேலே கொடுக்கப்பட்டுள்ள சதுரம் ABCD இல், ஒவ்வொரு பக்கமும் 1 செ.மீ அலகுகளாகப் பிரிக்கப்பட்டுள்ளது.

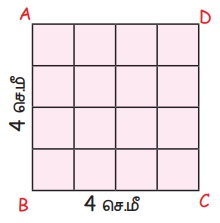
எதிரெதிர்ப் பக்கங்களின் மீதுள்ள புள்ளிகள் மேலேயுள்ள படத்தில் காட்டியுள்ளவாறு இணைக்கப்பட்டுள்ளன. சதுரம் ABCD ஒவ்வொன்றிலும் 4 சதுரங்கள் உள்ளவாறு 4 வரிசைகள் உருவாக்கப்பட்டுள்ளன. அவ்வாறு உருவாக்கப்பட்ட ஒவ்வொரு சதுரமும் 1 செ.மீ பக்க அளவைக் கொண்டிருக்கும். எனவே, ஒவ்வொரு சதுரத்தின் பரப்பளவும் 1 சதுர செ.மீ  ஆகும். இது அலகு சதுரம் எனப்படுகிறது.

மேலே கொடுக்கப்பட்டுள்ள சதுரத்தைக் கவனிக்க .சதுரத்தின் பக்க அளவு 4 செ.மீ ஆகும் மற்றும் அந்த சதுரத்தினுள் 1 செ.மீ பக்க அளவுள்ள 16 சதுரங்களை நாம் பெற்றிருக்கிறோம். மேலும்,

சதுரத்தின் பக்க அளவு 4 செ.மீ எனில், அச்சதுரத்தின் பரப்பளவு = 4 × 4 = 16 சதுர செ.மீ 

அவ்வாறு கிடைக்கப்பெற்ற ஓரலகுச் சதுரங்களின் எண்ணிக்கையானது சதுரத்தின் இரண்டு பக்க அளவுகளின் பெருக்கல்பலனுக்குச் சமமாகும்.

எனவே, சதுரத்தின் பரப்பளவு = பக்கம் × பக்கம்

பரப்பளவு காணும்போது, ஒவ்வொரு முறையும், சதுரம் மற்றும் செவ்வகங்களை ஓரலகு சதுரங்களாகப் பிரிக்க வேண்டிய அவசியமில்லை. சரியான மதிப்புகளைப் பிரதியிட்டு எளிமையான முறையில் பரப்பளவைக் காணச் சூத்திரங்களே பெரிதும் பயன்படுகிறது.

எடுத்துக்காட்டு 1.5

நீளம் 10 செ.மீ மற்றும் அகலம் 8 செ.மீ அளவுள்ள செவ்வகத்தின் பரப்பளவைக் காண்க. 

தீர்வு

செவ்வகத்தின் பரப்பளவு = நீளம் × அகலம்

= 10 × 8

= 80

எனவே, செவ்வகத்தின் பரப்பளவு 80 ச.செ.மீ ஆகும்.

எடுத்துக்காட்டு 1.6

6 மீ நீளமும் 2 மீ அகலமும் கொண்ட ஒரு சுவருக்கு வண்ணம் பூசப்பட வேண்டும். ஒரு சதுர மீட்டருக்கு ரூ 20 உழைப்பூதியம் எனில், சுவருக்கு வண்ணம் பூச ஆகும் உழைப்பூதியத்தைக் காண்க.

தீர்வு

முதலில் வண்ணம் பூசப்பட வேண்டிய சுவரின் பரப்பளவைக் கணக்கிடுவோம்.

சுவரின் பரப்பளவு = சுவரின் நீளம் × சுவரின் அகலம்

= 6 × 2 = 12.

அதாவது, சுவரின் பரப்பளவு 12 ச.மீ ஆகும்.

ஒரு சதுர மீட்டருக்கு வண்ணம் பூச உழைப்பூதியம் ₹ 20 ஆகும்.

எனவே, 12 சதுர மீட்டருக்கான உழைப்பூதியம் = 12 × 20 = ₹ 240.

எனவே, சுவருக்கு வண்ணம் பூச ஆகும் உழைப்பூதியம் ₹ 240 ஆகும்.

எடுத்துக்காட்டு 1.7

12 செ.மீ பக்க அளவுள்ள சதுரத்தின் பரப்பளவு என்ன?

தீர்வு

சதுரத்தின் பரப்பளவு = பக்கம் × பக்கம்

= 12 × 12 = 144.

எனவே, சதுரத்தின் பரப்பளவு 144 ச.செ.மீ ஆகும்.

எடுத்துக்காட்டு 1.8

சதுர வடிவ தரையின் பக்க அளவு 3 மீ ஆகும். 1 ச.மீ.க்கு தரைப்பூச்சு செய்ய உழைப்பூதியம் ₹ 25 எனில் தரை முழுவதும் தரைப்பூச்சு செய்ய ஆகும் மொத்த உழைப்பூதியத்தைக் காண்க.

தீர்வு

முதலில், சதுரவடிவ தரையின் பரப்பளவைக் காண்போம்.

சதுரவடிவ தரையின் பரப்பளவு = பக்கம் × பக்கம்

= 3 × 3 = 9.

எனவே, சதுரவடிவ தரையின் பரப்பளவு 9 ச.மீ ஆகும்.

1 சதுர மீட்டருக்கு தரைப்பூச்சு செய்ய உழைப்பூதியம் ₹ 25 ஆகும்.

எனவே, 9 சதுர மீட்டருக்கு தரைப்பூச்சு செய்வதற்கான மொத்த உழைப்பூதியம் = 25 × 9

= ₹ 225.