நிகழ்தகவின் அடிப்படைக் கொள்கைகள் (Axioms of probability) - நிகழ்தகவு (Probability)

2. நிகழ்தகவின் அடிப்படைக் கொள்கைகள் (Axioms of probability)

S என்பது ஒரு சமவாய்ப்புச் சோதனையின் முடிவுற்ற கூறுவெளி. P(S) என்பது நிகழ்ச்சிகளின் தொகுப்பு எனவும், P என்பது P(S)-ல் வரையறுக்கப்படும் மெய்மதிப்புடைய சார்பு எனவும் கொள்க. P(A) என்பது கீழ்க்காணும் கொள்கைகளை நிறைவு செய்தால், A-வின் நிகழ்தகவு P(A) என அழைக்கப்படுகிறது.

• [P1] ஏதேனும் ஒரு நிகழ்ச்சி A-க்கு P(A) ≥ 0 (குறையற்ற எண் கொள்கை) (Non-negativity axiom)

• [P2] ஒன்றையொன்று விலக்கும் ஏதேனும் இரு நிகழ்ச்சிகள் A மற்றும் B- க்கு 

P(A ∪ B) = P(A) + P(B)       (கூட்டல் கொள்கை) (Additivity axiom)

• [P3] நிச்சய நிகழ்ச்சிக்கு, P(S) = 1 (சமப்படுத்துதல் கொள்கை) (Normalization axiom)

குறிப்பு 12.1

(i) 0 ≤ P(A) ≤ 1

(ii) A1,A2,A3, …., An என்பவை ஒன்றையொன்று விலக்கும் நிகழ்ச்சிகள் எனில்,

P(A1 ∪ A2, ∪ A3, ∪...∪ An) = P(A1) + P(A2) + P(A3) +...+ P(An)

முடிவுறு கூறுவெளிகள் உடைய நிகழ்தகவிற்கான சில தேற்றங்கள்(நிரூபணமின்றி)

கூறு வெளியிலுள்ள நிகழ்ச்சிகள் சமவாய்ப்பு நிகழ்ச்சிகள் எனில், தேற்றம் 12.1-யைப் பயன்படுத்தலாம். அவ்வாறில்லையெனில் தேற்றம் 12.2 -யைப் பயன்படுத்தலாம்.

தேற்றம் 12.1

S என்ற கூறுவெளியின் ஏதேனும் ஒரு உட்கணம் A என்க. எனில் P(A)என்பது [P1], [P2] மற்றும் [P3] என்ற நிகழ்தகவுக் கொள்கைகளை நிறைவு செய்யும்.

தேற்றம் 12.2

S = {a1, a2, a3, …, an} என்பது ஒரு முடிவுறு கூறுவெளி என்க. கூறுவெளி S -ல் உள்ள ஒவ்வொரு கூறுப்புள்ளி ai-க்கும் pi என்ற மெய் எண்ணுடன் தொடர்புபடுத்தி,

பின்வரும் பண்புகளை

(i) ஒவ்வொரு pi  ≥ 0. (ii) ∑ pi = p1 + p2 + p3 + … + pn = 1, நிறைவு செய்தால்

pi என்பது ai -ன் நிகழ்தகவு என அழைக்கப்படும்.

A என்ற நிகழ்ச்சியின் நிகழ்தகவு P(A) ஆனது A-ன் கூறுபுள்ளிகளின் நிகழ்தகவு கூடுதல் என வரையறுக்கப்பட்டால், P(A) என்ற சார்பானது [P1], [P2], மற்றும் [P3] என்ற நிகழ்தகவு கொள்கைகளை நிறைவு செய்யும்.

குறிப்பு: சில சமயங்களில் முடிவுறு கூறுவெளியிலுள்ள கூறுபுள்ளிகளையும் அதற்குரிய நிகழ்தகவுகளையும் பின்வருமாறு அட்டவணைப்படுத்தலாம்.

விளக்க எடுத்துக்காட்டு 12.6

(1) S = {1,2,3} என்க. என்பது S-ன் அடுக்குக்கணம் மற்றும் P(A) = n(A) / n(S) எனில் P({1}) = 1/3, P({2}) = 1/3 மற்றும் P({3}) = 1/3, ஆகியவை நிகழ்தகவின் அடிப்படை கொள்கைகள் [P1], [P2] மற்றும் [P3]-ஐ நிறைவு செய்யும். இங்குச் சோதனையின் எல்லா முடிவுகளும் சமவாய்ப்பு நிகழ்ச்சிகள் ஆகும்.

(2) S = {1,2,3}என்க. P(S)என்பது S-ன் அடுக்குக்கணம் ஆகும். A எனும் நிகழ்ச்சியில் உள்ள உறுப்புகளின் நிகழ்தகவின் கூடுதல், நிகழ்தகவு P(A) என வரையறுக்கப்பட்டால்

P({1}) = ½, P({2}) = ¼ மற்றும் P({3}) = ¼ , ஆகியவை நிகழ்தகவின் அடிப்படை கொள்கைகள் [P1], [P2] மற்றும் [P3] -ஐ நிறைவு செய்யும்.

(3) S = {1,2,3} மற்றும் P(S) என்பது S-ன் அடுக்குக்கணம் ஆகும். A எனும் நிகழ்ச்சியில் உள்ள உறுப்புகளின் நிகழ்தகவின் கூடுதல், நிகழ்தகவு P(A) என வரையறுக்கப்பட்டால்

P({1}) = 0, P({2}) = 1⁄√2 எனில் P({3}) =1- 1/√2, ஆகியவை நிகழ்தகவின் அடிப்படை கொள்கைகள் [P1], [P2] மற்றும் [P3] -ஐ நிறைவு செய்யும்.

(2) மற்றும் (3)-ல் சோதனையின் முடிவுகள் சமவாய்ப்பு நிகழ்ச்சிகள் அல்ல.

குறிப்பு 12.2

நிகழ்தகவின் மதிப்புகள் விகிதமுறா எண்களாகவும் இருக்கலாம்.

வகுப்பறைச் செயல்பாடு

ஒவ்வொரு மாணவரும் ஒரு நாணயத்தை 10 முறை சுண்டவேண்டும்.

p = (கிடைக்கும் தலைகளின் எண்ணிக்கை / 10 ) எனக் கணக்கிடுக.

அனைத்து மாணவர்களும் நாணயத்தை சுண்டும்போது கிடைக்கக்கூடிய தலைகளின் மொத்த எண்ணிக்கையின் விகிதம் காண்க. நாணயத்தைச் சுண்டும் எண்ணிக்கை அதிகரிக்கும் போது p → ½ என அறியலாம்.

எடுத்துக்காட்டு 12.1

A, B மற்றும் C என்ற ஒன்றையொன்று விலக்கிய மூன்று நிகழ்ச்சிகளை மட்டும் கொண்ட ஒரு சோதனையின் நிகழ்ச்சிகளின் நிகழ்தகவுகள் பின்வருமாறு கொடுக்கப்பட்டுள்ளன. இவை நிகழ்தகவிற்கான சாத்தியமானைவயா என ஆராய்க.

(i) P(A) = 4/7, P(B) = 1/7, P(C) = 2/7.

(ii) P(A) = 2/5, P(B) = 1/5, P(C) = 3/5.

(iii) P(A) = 0.3, P(B) = 0.9, P(C) = -0.2.

(iv) P(A) = 1/√3, P(B) = 1- 1/√3, P(C) = 0.

(v) P(A) = 0.421, P(B) = 0.527 P(C) = 0.042.

தீர்வு

ஒவ்வொரு சோதனையிலும் சரியான மூன்று ஒன்றையொன்று விலக்கிய நிகழ்ச்சிகள் மட்டுமே உள்ளன. எனவே அவை யாவுமளாவிய நிகழ்ச்சிகளாகும்.

⇒ S = A ∪ B ∪ C

எனவே நிகழ்தகவின் அடிப்படைக் கொள்கையின்படி

P(A) ≥ 0, P(B) ≥ 0, P(C) ≥ 0 மற்றும்

P(A∪B∪C) = P(A) + P(B) + P(C) = P(S) =1 ஆகும்

(i) P(A)= 4/7 ≥ 0, P(B) = 1/7 ≥  0 மற்றும் P(C) = 2/7 ≥ 0

P(S) = P(A) + P(B) + P(C) = 4/7 + 1/7 + 2/7 = 1

எனவே கொடுக்கப்பட்டுள்ள நிகழ்தகவுகள் சாத்தியமானவையே.

(ii) P(A) = 2/5 ≥ 0, P(B) = 1/5 ≥ 0 மற்றும் P(C) = 3/5 ≥ 0

ஆனால் P(S) =P(A) + P(B) + P(C) = 2/5 + 1/5 + 3/5 = 6/5 > 1

எனவே கொடுக்கப்பட்டுள்ள நிகழ்தகவுகள் சாத்தியமானதல்ல.

(iii) P(C) = - 0.2 ஒரு குறை எண்ணாயிருப்பதால் கொடுக்கப்பட்டுள்ள நிகழ்தகவுகள் சாத்தியமானதல்ல

(iv) சாத்தியமானது. ஏனெனில்

P(A) = 1/ √3 ≥ 0, P(B) = 1 – 1/ √3 ≥ 0 மற்றும் P(C) = 0 ≥ 0

மேலும் P(S) = P(A) + P(B) + P(C) = 1 / √3 + 1 – 1 / √3 + 0 = 1.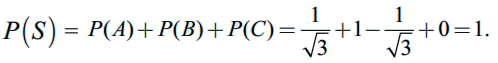

(v) P(A) = 0.421 ≥ 0, P(B) = 0.527 ≥ 0 மற்றும் P(C) = 0.042 ≥ 0

என இருந்தாலும்,

P(S) = P(A) + P(B) + P(C) = 0.421 + 0.527 + 0.042 = 0.990 < 1 என்பதால் கொடுக்கப்பட்ட நிகழ்தகவுகள் சாத்தியமற்றவை.

எடுத்துக்காட்டு 12.2

முதல் 10 மிகை முழு எண்களில் இருந்து ஒரு எண் தேர்ந்தெடுக்கப்படுகிறது. அந்த எண் (i) இரட்டைப் படை (ii) மூன்றின் மடங்காக இருப்பதற்கான நிகழ்தகவைக் காண்க.

தீர்வு

கூறுவெளி S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, n(S) = 10

A என்பது இரட்டைப்படை எண் கிடைக்கும் நிகழ்ச்சி என்க.

B என்பது மூன்றின் மடங்கு கிடைக்கும் நிகழ்ச்சி என்க.

A = {2, 4, 6, 8,10}, n(A) = 5,

B = {3, 6, 9}, n(B) = 3

P (இரட்டைப்படை எண் கிடைக்க ) = P(A) = n(A) / n(S) = 5/10 = 1/2.

P (மூன்றின் மடங்கு கிடைக்க) = P(B) = n(B) / n(S) =3/10.

எடுத்துக்காட்டு 12.3

மூன்று நாணயங்கள் ஒரே சமயத்தில் சுண்டப்படுகின்றன. (i) சரியாக ஒரு தலை (ii) குறைந்தது ஒரு தலை (ii) அதிகபட்சமாக ஒரு தலை கிடைப்பதற்கான நிகழ்தகவுகளைக் காண்க. 

தீர்வு

மூன்று நாணயங்களைச் ஒரு முறை சுண்டுவதும் ஒரே நாணயத்தை மூன்று முறைச்சுண்டுவதும் ஒன்றே என்பதைக் கவனிக்கவும். 

கூறுவெளி S = {H,T}×{H,T}×{H,T} 

S = {HHH,HHT, HTH,THH, HTT,THT,TTH,TTT}, n(S) = 8

A என்பது ஒரு தலை விழும் நிகழ்ச்சி, B என்பது குறைந்தபட்சம் ஒரு தலை விழும் நிகழ்ச்சி மற்றும் C என்பது அதிகபட்சமாக ஒரு தலை விழும் நிகழ்ச்சி என்க.

A = {HTT,THT,TTH}; n(A) = 3

B = {HTT,THT, TTH, HHT, HTH,THH, HHH}; n(B) =7

C = {TTT, HTT, THT,TTH}; n(C) = 4.

எனவே தேவைப்படும் நிகழ்தகவுகள்

(i) P(A) = n(A) / n(S) = 3/8

(ii) P(B) = n(B) / n(S) = 7/8

(iii) P(C) = n(C) / n(S) = 4/8 = 1/2 

குறிப்பு 12.3

கூறுவெளியில் உள்ள உறுப்புகளின் உறுப்புகளின் எண்ணிக்கை மிகவும் சிறிய அளவில் இருந்தால் கூறுவெளியின் உறுப்புகளை விரல் விட்டு எண்ணிவிடலாம். ஆனால் உறுப்புகளின் எண்ணிக்கை மிக அதிக அளவில் இருந்தால் சேர்ப்பியல் (Combinatorices) முறையைப் பயன்படுத்திக் கூறுவெளியில் உள்ள உறுப்புகளின் எண்ணிக்கையைக் கணக்கிடலாம்.

பின்வரும் கணக்கில் உள்ள உறுப்புகளின் எண்ணிக்கையைச் சேர்ப்பியலைப் பயன்படுத்திக் கணக்கிடலாம்.

எடுத்துக்காட்டு 12.4

பத்து நாணயங்கள் சுண்டப்படுகின்றன (i) சரியாக இரு தலைகள் (ii) அதிகபட்சமாக இரண்டு தலைகள் (iii) குறைந்தது இரண்டு தலைகள் கிடைப்பதற்கான நிகழ்தகவினைக் காண்க.

தீர்வு

ஒரே நேரத்தில் பத்து நாணயங்களைச் சுண்டுவதும், ஒரே நாணயத்தைப் பத்துமுறை சுண்டுவதும் ஒரே கூறுவெளியைக் கொடுக்கும்.

A என்பது சரியாக இரு தலைகள் கிடைப்பதற்கான நிகழ்ச்சி

B என்பது அதிகபட்சமாக இரு தலைகள் கிடைப்பதற்கான நிகழ்ச்சி மற்றும்

C என்பது குறைந்தபட்சம் இரு தலைகள் கிடைப்பதற்கான நிகழ்ச்சி என்க. 

பத்து நாணயங்கள் சுண்டப்படும்போது கூறுவெளியின் உள்ள

உறுப்புகளின் எண்ணிக்கை 2n = 210 =1024

n(S) = 1024

n(A) = 10C2  = 45

n(B) = 10C0 + 10C1 + 10C2 = 1 + 10 + 45 = 56

n(C) = 10C2 + 10C3 + 10C4 + … + 10C10

= n(S) - (10C0 + 10C1) = 1024 – 11 = 1013

தேவையான நிகழ்தகவுகள்

(i) P(A) = n(A) / n(S) = 45/1024

(ii) P(B) = n(B) / n(S) = 56/1024 = 7/128

(iii) P(C) = n(C) / n(S) = 1013/1024

எடுத்துக்காட்டு 12.5

ஒரு சீரான பகடையை ஒரு முறை உருட்டி விடும்போது

(i) இரட்டைப்படை எண் (ii) மூன்றின் மடங்காக கிடைப்பதற்கான நிகழ்தகவைக் காண்க.

தீர்வு

S என்பது கூறுவெளி, A என்பது இரட்டைப்படை எண் மற்றும்

B என்பது மூன்றின் மடங்காகக் கிடைப்பதற்கான நிகழ்ச்சி என்க.

எனவே

S = {1,2,3,4,5,6}  ⇒ n(S) = 6

A ={2,4,6}           ⇒ n(A) = 3

B = {3,6}             ⇒ n(B) = 2

தேவையான நிகழ்தகவுகள்.

(i) P (இரட்டைப்படை எண் கிடைக்க) = P(A) = n(A)/n(S) = 3/6 = 1/2

(ii) P (மூன்றின் மடங்கு கிடைக்க) = P(B) = n(B) / n(S) = 2/6 = 1/3.

எடுத்துக்காட்டு 12.6

ஒரு சோடிப் பகடைகளை உருட்டி விடும்போது அவற்றின் கூட்டுத் தொகை

(i) 7 (ii) 7 அல்லது 9 (iii) 7 அல்லது 12 கிடைப்பதற்கான நிகழ்தகவைக் காண்க? 

தீர்வு

கூறுவெளி S = {1, 2, 3, 4, 5, 6} × {1, 2, 3, 4, 5, 6}

S = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6),

(2,1), (2,2), (2,3), (2,4), (2,5), (2,6), 

(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),

(4,1), (4,2), (4,3), (4,4), (4,5), (4,6),

(5,1), (5,2), (5,3), (5,4), (5,5), (5,6),

(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}

நிகழக்கூடிய மொத்த நிகழ்ச்சிகள் = 62 = 36 = n(S)

A என்பது கூடுதல் 7 கிடைக்கும் நிகழ்ச்சி, B என்பது கூடுதல் 9 கிடைக்கும் நிகழ்ச்சி மற்றும்

C என்பது கூடுதல் 12 கிடைக்கும் நிகழ்ச்சி என்க.

A = {(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)}   ⇒ n(A) = 6

B = {(3,6),(4,5), (5,4), (6,3)}                       ⇒ n(B) = 4

C = {(6,6)}                                                   ⇒ n(C) = 1

 (i) P (கூடுதல் 7 கிடைக்க ) = P(A)

= n(A) / n(S) = 6/36 = 1/6

(ii) P (7 அல்லது 9 கிடைக்க) = P(A அல்லது B) = P (A ∪ B)

= P(A) + P(B)

(A மற்றும் B ஒன்றையொன்று விலக்கிய நிகழ்ச்சிகள், A ∩ B = Ø)

= n(A) / n(S) + n(B)/n(S) = 6/36 + 4/36 = 5/18

(iii) P (7 அல்லது 12 கிடைக்க ) = P(A அல்லது C) = P(A ∪ C)

= P(A) + P(C)

( A மற்றும் C ஒன்றையொன்று விலக்கிய நிகழ்ச்சிகள்)

= n(A) / n(S) + n(C)/n(S) = 6/36 + 1/36 = 7/36

எடுத்துக்காட்டு 12.7

நடப்பு ஆண்டுக்கான FIDE சதுரங்கப் போட்டியில் (World Chess Federa- tion) கோப்பையை வென்றிட X, Y மற்றும் Z என்ற மூன்று நபர்கள் போட்டியிடுகின்றனர். X-ன் வெற்றி வாய்ப்பு Y -ன் வெற்றி வாய்ப்பைப் போல 3 மடங்காக இருக்கும். Y-ன் வெற்றி வாய்ப்பு Z-ன் வெற்றி வாய்ப்பைப் போல 2 மடங்காக இருக்கும் எனில் ஒவ்வொருவரும் கோப்பையை வெல்லுவதற்கான நிகழ்தகவைக் காண்க.

தீர்வு

நடப்பு ஆண்டுக்கான FIDE கோப்பையை X, Y மற்றும் Z வெற்றிபெறும் நிகழ்ச்சிகளை A, B மற்றும் C என்க. X-ன் வெற்றி வாய்ப்பு Y -ன் வெற்றி வாய்ப்பைப் போல 3 மடங்காக இருக்கும். எனக் கொடுக்கப்பட்டுள்ளது. எனவே

A : B : : 3 : 1.               (1)

Y-ன் வெற்றி வாய்ப்பு Z-ன் வெற்றி வாய்ப்பைப் போல 2 மடங்காக இருக்கும். எனவே

B : C : : 2 : 1               (2)

(1) மற்றும் (2)-லிருந்து

A: B : C: : 6 : 2 : 1

A = 6k, B = 2k, C = k, இங்கு k என்பது ஒரு விகித மாறிலி ஆகும்.

கோப்பையை X வெல்வதற்கான நிகழ்தகவு P(A) = 6k/9k = 2/3

கோப்பையை Y வெல்வதற்கான நிகழ்தகவு P(B) = 2k / 9k = 2/9 மற்றும்

கோப்பையை Z வெல்வதற்கான நிகழ்தகவு P(C) = k/9k = 1/9

எடுத்துக்காட்டு 12.8

மூன்று வெவ்வேறு நபர்களுக்கு மூன்று கடிதங்கள் எழுதப்பட்டு மூன்று உறைகளில் வைக்கப்பட்டு அவர்களுக்கான விலாசமும் எழுதப்பட்டுள்ளன. முகவரியைப் பார்க்காமலே கடிதங்களை உறையிலிடும்போது (i) ஒரு கடிதம் சரியான உறையிலிட (ii) எல்லாக் கடிதங்களுமே தவறாக உறையிலிட நிகழ்தகவுகளைக் காண்க. 

தீர்வு

A, B மற்றும் C என்பவை உறைகளைக் குறிக்கும் என்க. 1, 2 மற்றும் 3 ஆனது முறையே A, B மற்றும் C-க்கான கடிதங்களைக் குறிக்கும் என்க.

கடிதங்களை உறைகளில் இடுவதற்கான எல்லா சாத்தியக் கூறுகளும் அட்டவணையில் கொடுக்கப்பட்டுள்ளன.

ci என்பது கிடைக்க கூடிய நிகழ்ச்சி என்க. 

X என்பது ஒரு கடிதம் மட்டும் சரியான உறையிலிடும் நிகழ்ச்சி என்க.

Y என்பது மூன்று கடிதங்களுமே தவறாக உறையிலிடுவதற்கான நிகழ்ச்சி என்க.

S = {C1, C2, C3, C4, C5, C6}, n(S) = 6

X = {C2,C3,C6},   n(X) = 3

Y = { C4, C5}       n(Y) = 2

(i) P(X) = 3/6 = 1/2 

(ii) P(Y) = 2/6 = 1/3

எடுத்துக்காட்டு 12.9

என்பது M என்ற அணி என்க. சமவாய்ப்பு முறையில் x, y மற்றும் z ன் மதிப்புகள், {1, 2,3} என்ற கணத்திலிருந்து மதிப்புக்களைப் பெறலாம். மேலும் மதிப்புகள் திரும்பத் திரும்பப் பயன்படுத்தலாம் (அதாவது, x = y = z) எனில், அணி M ஆனது பூச்சிய கோவை அணியாக இருப்பதற்கான நிகழ்தகவு என்ன?

தீர்வு

M என்பது பூச்சிய கோவை அணி எனில் . அதாவது, x − yz = 0. (x,y,z) -களை தேர்வு செய்யவேண்டிய வாய்ப்புகளுக்கான கணம், {(1,1,1),(2,1,2),(2,2,1),(3,1,3),(3,3,1)} = A என்க.

சாதகமான நிகழ்ச்சிகளின் எண்ணிக்கை n(A) = 5

மொத்த நிகழ்ச்சிகளின் எண்ணிக்கை n(S) = 33 = 27

கொடுத்துள்ள அணி பூஜ்ஜியக் கோவை அணியாக இருப்பதற்கான நிகழ்தகவு P(A) = n(A) / n(S) = 5/27

எடுத்துக்காட்டு 12.10

ஒரு விளையாட்டுப் போட்டியில் வெற்றி பெறுபவர் ஏறும் வெற்றி மேடையானது படத்தில் உள்ளவாறு மூன்று நிலைகளாக அமைக்கப்பட்டுள்ளன. சிவப்பு வர்ணம் உட்பட ஆறு வர்ணங்களைக் கொண்டு மூன்று நிலைகளுக்கும் வெவ்வேறான வர்ணங்கள் பூச வேண்டும். சிறிய நிலை மேடைக்கு (3வது நிலை) சிவப்பு வர்ணம் பூசப்படுவதற்கான நிகழ்தகவு என்ன?

தீர்வு

S என்பது கூறுவெளி என்க.

A என்பது சிறிய நிலை (3 வது நிலை) சிவப்பு வர்ணம் பூசும் நிகழ்ச்சி என்க.

n(S) = 6P3 = 6 × 5 × 4 = 120 

n(A) = 5 × 4 = 20

P(A) = n(A) / n(S) =20/120 = 1/6