வேற்றினப் பின்னங்களை ஒப்பிடுதல்

வேற்றினப் பின்னங்களை ஒப்பிடுதல்

கீழ்க்கண்ட சூழல்கள் குறித்துச் சிந்திக்க

சூழல் 1

முருகன் கணிதத் தேர்வில் 10 இக்கு 9 மதிப்பெண்ணும் மற்றும் அறிவியல் தேர்வில் 10 இக்கு 7 மதிப்பெண்ணும் பெற்றுள்ளார் எனில், எந்தப் பாடத்தில் அவர் சிறந்த மதிப்பெண்ணைப் பெற்றுள்ளார்? கணிதப் பாடத்தில் தான் சிறந்த மதிப்பெண்ணைப் பெற்றுள்ளார் என்று எளிதில் கூறலாம். ஏனெனில் இரு தேர்வுகளும் 10 மதிப்பெண்களுக்கு நடத்தப்பட்டுள்ளது. ஆனால் இரண்டு கணிதத் தேர்வுகளில் முருகன் பெற்றுள்ள மதிப்பெண்களான மற்றும் ஐ வைத்து, எத்தேர்வில் அவர் சிறப்பாக எழுதியுள்ளார் என்று கண்டறிய முடியுமா? அவ்வாறு கண்டறிய வேற்றினப் பின்னத்தில் உள்ள மதிப்பெண்களை ஓரினப் பின்னங்களாக மாற்ற வேண்டும்.

இன் சமானப் பின்னம் ஆகும். இந்த மதிப்பெண்ணை, இரண்டாவது தேர்வின் மதிப்பெண்ணோடு ஒப்பிட்டுப் பார்க்க முடியும். ஏனெனில் இரண்டு தேர்வின் மதிப்பெண்களும் 20 இக்கு எவ்வளவு பெற்றுள்ளார் என்று இருக்கிறது. இங்கு தொகுதியை ஒப்பிட்டால் 18 > 13, எனவே . ஆகவே முருகன் முதல் தேர்வைச் சிறப்பாகச் செய்துள்ளார்.

சூழல் 2

ஒரு வளைகோல் பந்துத் தொடர் போட்டியில் A என்ற அணி 6 போட்டிகளில் விளையாடி, 5 போட்டிகளில் வெற்றி பெற்றது. B என்ற அணி 5 போட்டிகளில் விளையாடி, 4 போட்டிகளில் வெற்றி பெற்றது. இவ்விரு அணிகளும் இவ்விதமாகவே தொடர்ந்து விளையாடினால், எந்த அணி தொடர் போட்டியில் வெற்றி பெறும் ?

இதற்கு நாம் மற்றும் இல் எது பெரியது எனக் காண வேண்டும். இதை எப்படிக் கண்டறிவது? ஒவ்வொரு அணியும் விளையாடிய மொத்தப் போட்டிகளின் எண்ணிக்கை வேறுபடுகிறது. மற்றும் இக்குச் சமான பின்னங்களைக் கண்டறிந்து அணி A மற்றும் அணி B ஆல் விளையாடப்பட்ட போட்டிகளின் எண்ணிக்கையைச் சமமாக்கலாம்.

மற்றும்

இவற்றின் சமானப் பின்னங்களின் பொதுவான பகுதி 30 ஆக அமைகிறது. அதாவது 5 × 6 அல்லது 6 × 5. இது 5 மற்றும் 6 இன் பொது மடங்கு ஆகும். 

இங்கு, . ஆகவே அணி A வெற்றி பெறும்.

குறிப்பு

இரண்டு அல்லது அதற்கு மேற்பட்ட வேற்றினப் பின்னங்களை ஒப்பிட, நாம் முதலில் அவற்றை ஓரினப்பின்னங்களாக மாற்ற வேண்டும். இந்த ஓரினப்பின்னங்கள் கொடுக்கப்பட்ட பின்னங்களின் சமானப் பின்னங்களாகும். ஓரினப் பின்னங்களின் பகுதிகளானது கொடுக்கப்பட்ட வேற்றினப் பின்னப் பகுதிகளின் மீச்சிறு பொது மடங்கு ஆகும்.

எடுத்துக்காட்டு 2

மதி ஒரு சாக்லெட் கட்டியில் பகுதியைச் சாப்பிட்டார். நந்தினி அதேபோன்ற மற்றொரு சாக்லெட் கட்டியில் பகுதியைச் சாப்பிட்டார் எனில், அதிகமான சாக்லெட் பகுதியைச் சாப்பிட்டவர் யார்?

தீர்வு

மதியால் சாப்பிடப்பட்ட சாக்லெட்டின் அளவு =

நந்தினியால் சாப்பிடப்பட்ட சாக்லெட்டின் அளவு =

இங்கு, அவர்களால் சாப்பிடப்பட்ட சாக்லெட்டுகளின் அளவு வேறுபடுகின்றன. அந்த அளவினைச் சமமாக்க, அவற்றின் சமானப் பின்னங்களைக் கண்டறிய வேண்டும்.

மற்றும் ஆகியவற்றின் சமானப் பின்னங்களின் பொதுப் பகுதியானது அவ்விரு பின்னப் பகுதிகளுக்குக் கண்டறியப்படும் மீச்சிறு பொது மடங்கிற்குச் சமம்.

எனவே,  மற்றும் ஆகவே,

ஆகையால், மதி அதிகமான சாக்லெட் பகுதிகளைச் சாப்பிட்டுள்ளார் என முடிவு செய்யலாம்.

குறிப்பு: கொடுக்கப்பட்ட வேற்றினப் பின்னங்களை ஓரினப் பின்னங்களாக மாற்றும் முறையை எளிமையாக்க அவ்வேற்றினப் பின்னங்களின் பகுதிகளுக்கு மீச்சிறு பொது மடங்கினைக் கண்டுபிடித்தலே போதுமானதாக இருக்கும்.

எடுத்துக்காட்டு 3

வினோதா, செந்தமிழ் மற்றும் முகிலரசி ஆகியோர் நீர் நிரப்பும் போட்டியில் பங்கேற்கிறார்கள். அவர்கள் ஒவ்வொருவருக்கும் 30 வினாடிக்குள் நீர் நிரப்ப வேண்டி சமக் கொள்ளளவைக் கொண்ட புட்டிகள் வழங்கப்பட்டன. வினோதா தன் புட்டியில் பகுதியும், செந்தமிழ் தன் புட்டியில் பகுதியும், முகிலரசி தன் புட்டியில் பகுதியும் நிரப்பினார்கள் எனில், முதலாவது, இரண்டாவது மற்றும் மூன்றாவது பரிசு யாருக்குக் கிடைக்கும்?

தீர்வு

கொடுக்கப்பட்ட பின்னங்களின் பகுதியானது, 4ஆக அமையும் வரை சமானப் பின்னங்களை எழுதவும். இது 2 மற்றும் 4 இன் மீச்சிறு பொது மடங்கு ஆகும்.

இன் சமானப் பின்னம் ஆகும்.

இங்கு, < < எனவே, செந்தமிழ் முதல் பரிசையும், வினோதா இரண்டாவது பரிசையும், முகிலரசி மூன்றாவது பரிசையும் பெறுவார்கள்.

எடுத்துக்காட்டு 4

உங்களுக்குத் தெரியுமா?

ஓரலகு பின்னங்களை ஒப்பிடுதல்: ஒரு பின்னத்தின் தொகுதி 1 ஆக இருப்பின், அப்பின்னம் ஓரலகு பின்னம் எனப்படும். எடுத்துக்காட்டாக 1/7 மற்றும் 1/5 ஐ ஒப்பிடுக.

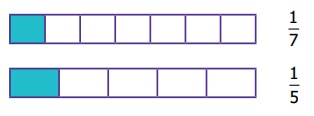
படத்திலிருந்து 1/5 > 1/7 எனக் கண்டறியலாம். ஆகவே, ஓரலகு பின்னங்களில் பெரிய பகுதியைப் பெற்றுள்ள பின்னமே சிறிய பின்னமாக அமையும். எனவே, ஒரே தொகுதியை உடைய இரண்டு பின்னங்களில் சிறிய பகுதியைக் கொண்டுள்ள பின்னமே அவற்றுள் பெரிய பின்னமாக அமையும் என்ற முடிவுக்கு வரலாம்.

இவற்றை முயல்க

1. கொடுக்கப்பட்ட சோடி பின்னத்தைக் குறிக்கும் செவ்வகங்களை நிழலிட்டு, அவற்றுள் எது பெரியது எனக் கூறுக.

தீர்வு : 

விடை: 3/5

2. அல்லது இல் எது பெரியது?

தீர்வு : 

3. 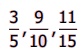ஆகிய பின்னங்களை ஏறுவரிசையில் அமைக்க.

தீர்வு : 

ஏறுவரிசை: 3/5 , 11/15, 9/10 

4. ஆகிய பின்னங்களை இறங்கு வரிசையில் அமைக்க.

தீர்வு :