வட்ட இயக்கத்தின் இயக்க விசையியல்

வட்ட இயக்கத்தின் இயக்க விசையியல் 

முற்பகுதியில் நியூட்டனின் விதிகளைப் பயன்படுத்தி பொருட்களின் நேர்க்கோட்டு இயக்கத்தை எவ்வாறு பகுப்பாய்வு செய்வது என்று அறிந்து கொண்டோம். இதே போன்று நியூட்டனின் விதிகளை வட்டஇயக்கத்திற்கு எவ்வாறு பயன்படுத்துவது என்று அறிந்து கொள்வதும் அவசியமாகும். 

ஏனெனில் வட்ட இயக்கம் நம் வாழ்க்கையில் தவிர்க்க முடியாத ஒன்றாகும். புறவிசை செயல்பட்டாலும் அல்லது செயல்ப டாவிட்டாலும் ஒரு பொருளானது நேர்க்கோட்டு இயக்கத்தை மேற்கொள்ளலாம். ஆனால் பொருளின்மீது விசை செயல்பட்டால் மட்டுமே வட்ட இயக்கம் சாத்தியமாகும். வட்ட இயக்கத்திற்கு நியூட்டனின் முதல் விதி என்ற ஒன்று இல்லை. அதாவது பொருளின்மீது விசை செயல்படாமல் அப்பொருளினால் வட்ட இயக்கத்தை மேற்கொள்ள இயலாது. பொருளின்மீது செயல்படும் விசை அப்பொருளின் திசைவேகத்தை மூன்று வழிகளில் மாற்றியமைக்கும். 

1) திசைவேகத்தின் திசையை மாற்றாமலேயே அதன் எண்மதிப்பை மட்டும் மாற்றுவது. இந்நிகழ்வில் துகள் ஒரே திசையில் முடுக்கத்துடன் இயங்கும்.

எடுத்துக் காட்டுகள் 

செங்குத்தாகக் கீழே விழும் பொருள், முடுக்கத்துடன் நேரான சாலையில் செல்லும் வாகனம் 

2) திசைவேகத்தின் எண்மதிப்பை (வேகம்) மாற்றாமல் அதன் திசையை மட்டும் மாற்றுவது. இவ்வாறு இயங்கும் இயக்கதை நாம் சீரான வட்ட இயக்கம் என்று அழைக்கிறோம். 

3) திசைவேகத்தின் எண்மதிப்பு (வேகம்) மற்றும் திசை இவ்விரண்டிலும் மாற்றம் ஏற்பட்டால் வட்டமற்ற இயக்கம் ஏற்படும் (Non circular motion) எடுத்துக்காட்டுகள் 

ஊஞ்சல், தனி ஊசல், நீள் வட்டப்பாதையில் சூரியனைச் சுற்றி வரும் கோள்களின் இயக்கம் போன்றவை. 

இப்பிரிவில் சீரான வட்ட இயக்கம் மற்றும் சீரற்ற வட்ட இயக்கங்களைப் பற்றி அறியலாம்.

மையநோக்கு விசை 

துகளொன்று சீரான வட்டப்பாதையில் சுற்றி வரும்போது வட்டமையத்தை நோக்கி வட்டப்பாதையின் ஆரம் வழியாக மையநோக்கு முடுக்கம் ஏற்படும். நியூட்டனின் இரண்டாம் விதிப்படி முடுக்கம் ஏற்பட்டால் நிலைமக் குறிப்பாயத்தைப் பொருத்து துகளின்மீது ஒரு விசை செயல்பட வேண்டும். அவ்வாறு துகளின் மீது செயல்படும் விசையே மையநோக்கு விசை எனப்படும். 

அலகு 2 இல் நாம்கற்றபடி, வட்டப்பாதையில் இயங்கும் துகளின் மீது செயல்படும் மையநோக்கு முடுக்கம் a = v2/r ஆகும். இம்முடுக்கம் வட்டமையத்தை நோக்கிச் செயல்படுகிறது. நியூட்டனின் இரண்டாம் விதிப்படி, மையநோக்கு விசை

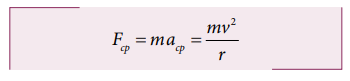
இங்கு மையநோக்கு விசை என்பதன் பொருள், துகள் வட்டப்பாதையில் எங்கு இருப்பினும் அதன் முடுக்கம் எப்போதும் மையத்தை நோக்கியே இருக்கும் என்பதைக் குறிக்கிறது.

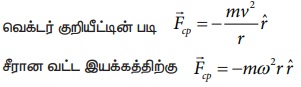
இங்கு -rˆ இன் திசை வட்ட மையத்தை நோக்கிக் குறிக்கிறது. மேலும் இதுவே மையநோக்கு விசையின் திசையைக் குறிக்கிறது. இதுபடம் 3.38 இல் தெளிவாக குறிப்பிட்டுக் காட்டப்பட்டுள்ளது.

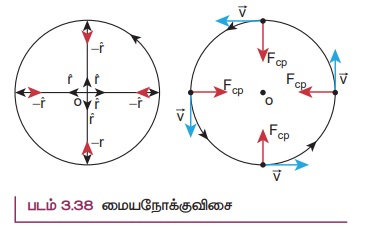
மையநோக்குவிசை, புவியீர்ப்பு விசை அல்லது சுருள்வில் விசை போன்ற ஒரு இயற்கை விசையல்ல என்பதை இங்கு கவனிக்க வேண்டும். மையத்தை நோக்கிச் செயல்படும் ஒரு விசை என்றே அழைக்கப்படுகிறது. புவியீர்ப்பு விசை, கயிற்றின் இழுவிசை, உராய்வு விசை, கூலும் விசை போன்ற ஏதேனும் ஒரு விசையே மையநோக்கு விசையாகச் செயல்படுகிறது. 

1) மெல்லிய கயிற்றின் ஒரு முனையில் கட்டி சுழற்றப்படும் கல்லின் இயக்கத்தில், கயிற்றின் இழுவிசையே மையநோக்கு விசையாகச் செயல்படுகிறது. பொழுதுபோக்குப் பூங்காக்களில் இயக்கப்படும் இராட்டினம் போன்ற சுழற்சி இயக்கத்தில், இராட்டினத்தைத் தாங்கும் இரும்புக் கம்பிகளின் இழுவிசை மையநோக்கு விசையை அளிக்கிறது. 

2) புவியினைச் சுற்றி வரும் செயற்கைக் கோளின் இயக்கத்தில், புவி, செயற்கைக் கோளின் மீது செலுத்தும் புவியீர்ப்பு விசையே மையநோக்கு விசையாகச் செயல்படுகிறது. செயற்கைக்கோள் இயக்கத்திற்கு நியூட்டனின் இரண்டாம் விதியை கீழ்காணுமாறு எழுதலாம்.

இங்கு r என்பது புவியின் மையத்திலிருந்து செயற்கைக்கோள் உள்ள தொலைவு

3) கார் ஒன்று வட்டவடிவப்பாதையில் செல்லும்போது, மையநோக்கு விசையானது காரின் டயருக்கும், சாலைக்கும் இடையே ஏற்படும் உராய்வு விசையினால் ஏற்படுகிறது.

இந்நிகழ்விற்கான நியூட்டன் இரண்டாம் விதியை கீழ்க்காணுமாறு எழுதலாம்.

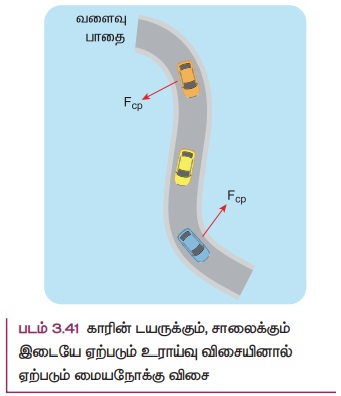
கார் வளைவுப் பாதையில் செல்லும் போதும், மையநோக்கு விசையைப் பெறுகிறது. காரின் டயருக்கும், சாலைக்கும் இடையே ஏற்படும் உராய்வு விசையினால் இம்மையநோக்கு விசை ஏற்படுகிறது. இது படம் 3.41 இல் காட்டப்பட்டுள்ளது.

4) கோள்கள் சூரியனைச் சுற்றி வரும்போது, அவை சூரியனின் மையத்தை நோக்கிய, ஒரு மையநோக்கு விசையைப் பெறுகின்றன. இங்கு கோள்களின் மீதான சூரியனின் ஈர்ப்பு விசை, மையநோக்கு விசையாகச் செயல்படுகிறது. இது படம் 3.42 இல் காட்டப்பட்டுள்ளது.

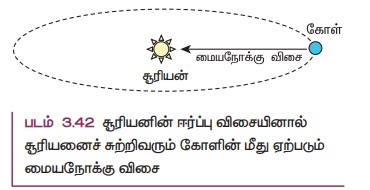
இந்நிகழ்விற்கான நியூட்டனின் இரண்டாம் விதியை பின்வருமாறு எழுதலாம். 

கோள்களின் மீது சூரியனின் ஈர்ப்புவிசை = mv2/r

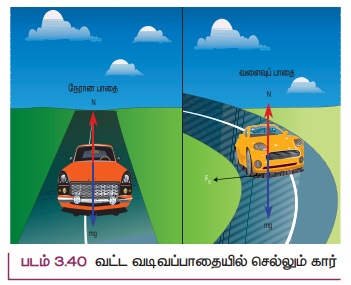
சரி சமமான வட்டச் சாலையில் செல்லும் வாகனம் 

வாகனமொன்று வளைவுப்பாதையில் செல்லும் போது, அவ்வாகனத்தின் மீது மையநோக்கு விசை செயல்படுகிறது. வாகனத்தின் டயர் மற்றும் சாலையின் மேற்பரப்பு இவற்றிற்கிடையேயான உராய்வு விசையின் காரணமாக இம்மையநோக்குவிசை ஏற்படுகிறது. m நிறையுடைய வாகனமொன்று r ஆரமுடைய வட்டவடிவப் பாதையில் v வேகத்தில் இயங்குகிறது எனில், அவ்வாகனத்தின் மீது மூன்று விசைகள் செயல்படுகின்றன. அவை படம் 3.43 இல் காட்டப்பட்டுள்ளன. 

1) கீழ்நோக்கிச் செயல்படும் புவிஈர்ப்புவிசை (mg) 

2) மேல்நோக்கிச் செயல்படும் செங்குத்துவிசை N 

3) சாலையின் கிடைத்தளப் பரப்பின் வழியே உள்நோக்கிச் செயல்படும் உராய்வு விசை (Fs) 

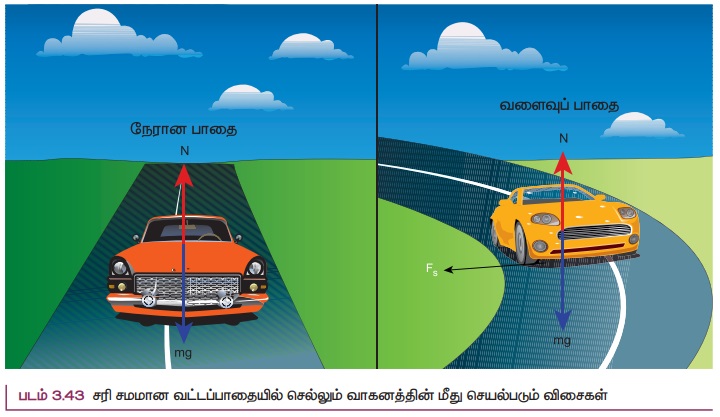
சாலை கிடைத்தளமாக இருப்பின், செங்குத்து விசையும், புவியீர்ப்பு விசையும் ஒன்றுக்கொன்று சமம் மற்றும் எதிரெதிராக இருக்கும். வாகனத்தின் டயருக்கும், சாலையின் பரப்பிற்கும் இடையே ஏற்படும் உராய்வு விசைதேவையான மையநோக்கு விசையை அளிக்கிறது. இம்மையநோக்கு விசை வட்டச்சாலையின் மையத்தை நோக்கிச் செயல்படுகிறது.

நாம் முற்பகுதியில் கற்றபடி, நிலை உராய்வு விசை சுழி முதல் பெரும மதிப்பு விசை வரை எந்த மதிப்பையும் பெறலாம். எனவே இங்கு இரண்டு நிபந்தனைகள் சாத்தியமாகிறது:

வளைவுச்சாலையில், வாகனம் வளைவதற்குத் தேவையான மையநோக்கு விசையை நிலை உராய்வு கொடுக்கிறது. எனவே வாகனத்தின் டயர் மற்றும் சாலையின் பரப்பு இவற்றிற்கிடையேயான நிலை உராய்வுக் குணகம் வாகனம் சறுக்காமல் வளைவுப்பாதையில் வளைவதற்கான பெருமவேகத்தை நிர்ணயிக்கிறது.

வாகனம் வளைவதற்குத் தேவையான மையநோக்கு விசையை நிலை உராய்வு விசையினால் கொடுக்க இயலவில்லை எனில், வாகனம் சறுக்கத் தொடங்கும்.

வெளிவிளிம்பு உயர்த்தப்பட்ட சாலை 

சரிசமமான வட்டச் சாலையில், வாகனங்கள் சறுக்கி விபத்துக்குள்ளாவது, சாலைப் பரப்பின் நிலை உராய்வு குணகத்தை சார்ந்திருக்கிறது. இந்த நிலை உராய்வுக் குணகத்தின் பெரும மதிப்பு பரப்பின் தன்மையைச் சார்ந்ததாகும். இதன் காரணமாக வாகனங்களுக்கு ஏற்படும் விபத்தினைத் தடுப்பதற்காகச் சாலையின் வெளிவிளிம்பு உட்புற விளிம்பை விட சற்றே உயர்த்தி அமைக்கப்பட்டிருக்கும். இதற்கு வெளிவிளிம்பு உயர்த்தப்பட்ட சாலை (banking of tracks) என்று பெயர். வெளிவிளிம்பு உயர்த்த ப்பட்டிருப்பதால் இது ஒரு சாய்தளம் போன்று அமையும். கிடைத்தளப் பரப்புடன் இந்தச் சாய்தளம் ஏற்படுத்தும் கோணம் வெளி விளிம்புக்கோணம் (banking angle) எனப்படும்.

கிடைத்தளத்துடன் θ கோணத்தில் உள்ள சாலையின் பரப்பைக் கருதுக. செங்குத்துவிசை, செங்குத்து அச்சுடன் இதே θ கோணத்தை ஏற்படுத்தும். இச்சாலையில் செல்லும் கார் ஒன்று வளையும்போது அதன் மீது இரண்டு விசைகள் செயல்படும். 

அ) கீழ்நோக்கிச் செயல்படும் புவியீர்ப்பு விசை (mg) 

ஆ) சாலையின் பரப்பிற்குச் செங்குத்தாகச் செயல்படும் செங்குத்து விசை (N) 

செங்குத்து விசை N ஐ இரண்டு கூறுகளாகப் பிரிக்கலாம். இவை N cosθ மற்றும் N sinθ ஆகும். இவை படம் 3.44 இல் காட்டப்பட்டுள்ளன. N cosθ கூறு, கீழ்நோக்கிச் செயல்படும் புவியிர்ப்பு விசையை (mg) சமன் செய்கிறது. N sinθ கூறு தேவையான மையநோக்கு விசையைக் கொடுக்கிறது. 

நியூட்டனின் இரண்டாம் விதியைப் பயன்படுத்தி பின்வரும் சமன்பாடுகளை அமைக்கலாம்.

வெளி விளிம்புக் கோணம் மற்றும் சாலையின் வளைவு ஆரம் (r) இவ்விரண்டும் வளைவுச் சாலையில் பாதுகாப்பாக வாகனங்களை இயக்க வேண்டிய வேகத்தைத் (v) தீர்மானிக்கின்றன. வாகனம் ஒன்றின் வேகம் நிர்ணயிக்கப்பட்ட வேகத்தைவிட அதிக வேகத்தில் செல்லும் போது சாலையின் வெளிப்புறத்தை நோக்கி சறுக்கத் தொடங்கும். ஆனால் உராய்வு விசை செயல்பட்டு கூடுதல் மையநோக்கு விசையினைக் கொடுத்து வெளிப்புறச் சறுக்குதலைத் தடுக்கும். அதேநேரத்தில் காரின் வேகம் நிர்ணயிக்கப்பட்ட வேகத்தை விட குறைவாக இருப்பின் கார் உட்புறத்தை நோக்கி நகரத் தொடங்கும். உராய்வு விசை செயல்பட்டு மையநோக்கு விசையைக் குறைத்து உட்புறத்தை நோக்கி சறுக்குவதைத் தடுக்கும். இருப்பினும் காரின் வேகம் மிக அதிகம் எனில் உராய்வு விசையினால் கார் சறுக்குவதைத் தடுக்க முடியாது.

மையவிலக்கு விசை 

வட்ட இயக்கத்தை இருவேறு குறிப்பாயங்களைப் பொருத்து ஆய்வு செய்யலாம். அவற்றுள் ஒன்று நிலைமக் குறிப்பாயமாகும். இக்குறிப்பாயம் ஓய்வுநிலை அல்லது சீரான இயக்கநிலை இவற்றுள் ஏதேனும் ஒரு நிலையில் இருக்கும். இங்கு இயக்கத்தில் உள்ள பொருட்கள் நியூட்டனின் இயக்க விதிகளுக்குக் கட்டுப்பட்டு இயங்கும். மற்றொரு குறிப்பாயம் முடுக்கமடைகின்ற, நிலைமமற்ற குறிப்பாயமான சுழற்சிக் குறிப்பாயமாகும் (rotational frames). வட்ட இயக்கத்தினை இவ்விரு குறிப்பாயங்களைப் பொருத்து வெவ்வேறு கண்ணோட்டத்தில் ஆய்வு செய்யலாம். சுழற்சிக் குறிப்பாயத்தில் நியூட்டனின் முதல் விதி மற்றும் இரண்டாம் விதியைப் பயன்படுத்தும் போது ஒரு போலியான விசையை (Pseudo force) சேர்த்துக் கருத வேண்டும். இந்தப் போலியான விசையே மையவிலக்கு விசையாகும். இத்தகைய மையவிலக்கு விசை சுழற்சிக் குறிப்பாயத்தைப் பொருத்து பொருளின் மீது செயல்படும். மையவிலக்கு விசையினைப் புரிந்து கொள்ள கீழ்க்கண்ட விளக்கம் பெரிதும் துணை புரியும். 

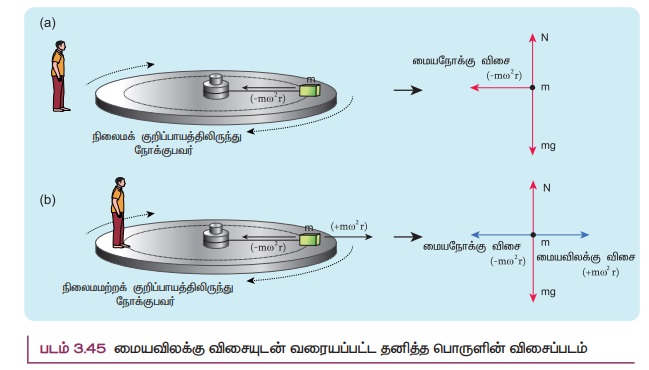
மெல்லிய கயிற்றின் ஒரு முனையில் கட்டப்பட்டு சுழற்சி இயக்கத்தை மேற்கொள்ளும் கல் ஒன்றைக் கருதுவோம். ஓய்வுநிலையிலுள்ள நிலைமக் குறிப்பாயத்தைப் பொருத்து கல்லின் கோணத் திசைவேகம் ω என்க. ω கோணத் திசைவேகத்தில் கல்லுடன் சேர்ந்து சுழற்சி இயக்கத்திலுள்ள மற்றொரு குறிப்பாயத்திலிருந்து கல்லினைப் பார்க்கும்போது அக்கல் ஓய்வுநிலையில் இருப்பது போன்று தோன்றும். 

சுழற்சிக் குறிப்பாயத்தைப் பொருத்து, வட்டமையத்தை நோக்கிச் செயல்படும் மையநோக்கு விசையான - mω2r உடன், அதற்குச் சமமான எதிர்திசையில் வெளிநோக்கிச் செயல்படும் + mω2r என்ற விசை கல்லின் மீது செயல்படுகிறது. எனவே சுழற்சி இயக்கத்திலுள்ள குறிப்பாயத்தைப் பொருத்து கல்லின் மீது செயல்படும் தொகுபயன் விசை சுழியாகும் என்பதை இது காட்டுகிறது. ( - mω2r + mω2r = 0) இங்கு வெளிநோக்கிச் செயல்படும் + mω2r விசைக்கு மையவிலக்கு விசை என்று பெயர். 

மையவிலக்கு என்பதன் பொருள் மையத்தை விட்டு வெளிநோக்கிச் செயல்ப டுவது என்பதாகும். சுழற்சிக் குறிப்பாயத்தைப் பொருத்து கல்லின் சுழற்சி இயக்கத்தை ஆய்வு செய்யும்போது மட்டும் மையவிலக்கு விசைகல்லின் மீது செயல்படுவதாகத் தோன்றும். இக்காரணத்தினால் தான் மையவிலக்கு விசையை ஒரு போலியான விசை என்று அழைக்கிறோம். இப்போலியான விசை எந்த மூலத்திலிருந்தும் தோன்றுவதில்லை (It has no origin). இங்கு போலி விசை தோன்றுவதற்கான காரணம், நாம் கருதும் சுழற்சி குறிப்பாயம் ஒரு நிலைமமற்ற குறிப்பாயம் என்பதாலே ஆகும். 

நிலைமக் குறிப்பாயத்தைப் பொருத்து கல்லின் சுழற்சி இயக்கத்தை ஆய்வு செய்யும்போது மையநோக்கு விசை மட்டுமே செயல்படும். இம்மையநோக்கு விசை கல் கட்டப்பட்டிருக்கும் மெல்லிய கயிற்றின் இழுவிசையால் பெறப்படுகிறது. சுழற்சி குறிப்பாயத்தை பொருத்து சுழற்சி இயக்கக் கணக்குகளைத் தீர்வு செய்ய வரையப்படும் தனித்த பொருளின் விசைப்படங்களில் படம் 3.45 இல் உள்ளவாறு மையவிலக்கு விசை கண்டிப்பாகக் காட்டப்பட வேண்டும்.

மைய விலக்கு விசையின் விளைவுகள் 

மையவிலக்கு விசை ஒரு போலியான விசையாக இருப்பினும் அதன் விளைவுகள் உண்மையாகும். கார் ஒன்று வளைவுப் பாதையில் திரும்பும்போது, காரின் உள்ளே அமர்ந்திருப்பவர் ஒரு வெளிப்புறவிசையை உணர்வார். அவ்விசை அவரை வெளிநோக்கித் தள்ளும். இவ்வெளிநோக்கிய விசையையும் மையவிலக்கு விசை என்றே அழைக்கலாம். காரின் இருக்கைக்கும், அமர்ந்திருக்கும் நபருக்கும் இடையே உள்ள போதுமான உராய்வு விசை இருந்தால் அவர் வெளியே தள்ளப்படுவது தவிர்க்கப்படுகிறது. 

நேர்க்கோட்டுப் பாதையில் சென்று கொண்டிருக்கும் கார் ஒன்று திடீரென்று தன்பாதையிலிருந்து வளையும்போது, காரின் உள்ளே நிலையாகப் பொருத்தப்படாத பொருள், திசையில் நிலைமப் பண்பின் (Inertia of direction) காரணமாக நேர்க்கோட்டுப் பாதையிலேயே தொடர்ந்து இயங்க முயற்சிக்கும்.

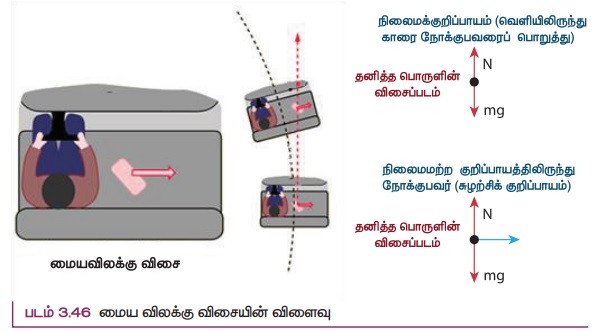
இவ்வியக்கத்தை நிலைமக் குறிப்பாயத்திலிருந்து பார்க்கும் போது படம் 3.46 இல் காட்டியுள்ளவாறு நேர்கோட்டு இயக்கமாகத் தெரியும். ஆனால் சுழற்சிக் குறிப்பாயத்திலிருந்து பார்க்கும்போது இயக்கம் வெளிநோக்கிச் செல்வது போன்று தோன்றும். சுழலும் மேடையில் நின்று கொண்டிருக்கும் நபர் வெளிப்புற மையவிலக்கு விசையை உணர்வார். இதன் காரணமாக மேடையிலிருந்து அவர் வெளியே தள்ளப்பட வாய்ப்பு அதிகம். நின்று கொண்டிருக்கும் நபருக்கும், மேடைக்குமான உராய்வுவிசை வெளிநோக்கித் தள்ளப்படும் விசையினைச் சமன் செய்யப் போதுமானதல்ல. இதனைத் தவிர்ப்பதற்காக மேடையின் வெளிப்புற விளிம்பு சற்றே மேல்நோக்கி உயர்த்தப்பட்டிருக்கும். இவ் உயர்வு நின்று கொண்டிருக்கும் நபரின் மீது ஒரு செங்குத்து விசையைச் செலுத்தி அவர் வெளியே விழுவதைத் தடுக்கும். இது படம் 3.47 இல் காட்டப்பட்டுள்ளது.

எச்சரிக்கை 

பேருந்தில் பயணம் செய்யும்போது திறந்திருக்கும் கதவு அல்லது படிக்கட்டில் நின்று கொண்டு பயணம் செய்வது மிகவும் ஆபத்தானது. பேருந்து வளைவுப்பாதையில் திடீரென்று வளையும் போது மையவிலக்கு விசையின் காரணமாக நின்று கொண்டிருக்கும் நபர் வெளிநோக்கித் தள்ளப்படலாம். மையவிலக்கு விசை ஒரு போலியான விசையாக இருப்பினும் அதன் விளைவுகள் உண்மையாகும்.

புவியின் சுழற்சியால் ஏற்படும் மையவிலக்கு விசை 

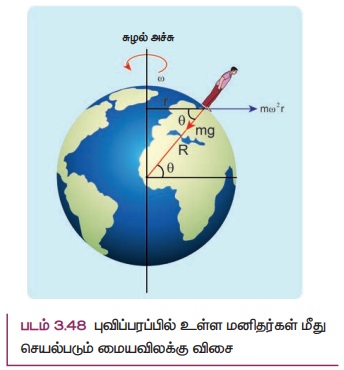
புவியினை ஒரு நிலைமக் குறிப்பாயமாகக் கருதினாலும் உண்மையில் அவ்வாறு இல்லை. புவி ω என்ற கோணத் திசைவேகத்தில் தன் அச்சினைப் பொருத்து தன்னைத்தானே சுற்றி வருகிறது. புவிப்பரப்பிலுள்ள எந்த ஒரு பொருளும் (சுழற்சிக் குறிப்பாயத்தில் உள்ள பொருள்) மைய விலக்கு விசையை உணரும். இம்மையவிலக்கு விசை சுழல் அச்சிலிருந்து மிகச் சரியாக எதிர் திசையில் செயல்படுவதாகத் தோன்றும். இது படம் 3.48 இல் காட்டப்பட்டுள்ளது 

புவிப்பரப்பில் நின்று கொண்டிருக்கும் மனிதரின் மையவிலக்கு விசை Fcf = mω2r 

இங்கு r என்பது சுழல் அச்சிற்கும் மனிதனுக்கும் இடையே உள்ள செங்குத்துத் தொலைவு. படம் 3.48 இல் காட்டப்பட்டுள்ளது. செங்கோண முக்கோணத்திலிருந்து தொலைவு r = R cosθ. இங்கு R என்பது புவியின் ஆரம். 

மேலும் θ என்பது மனிதன் நின்று கொண்டிருக்கும் புள்ளியில் புவியின் குறுக்குக் கோடு (latitude) ஆகும்.

மையநோக்கு விசை மற்றும் மையவிலக்கு விசை – ஓர் ஒப்பீடு: 

மையநோக்கு விசை மற்றும் மையவிலக்கு விசை ஆகியவற்றின் சிறப்புக் கூறுகள் அட்டவணை 3.4 இல் ஒப்பிட்டுக் காட்டப்பட்டுள்ளன.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் மையநோக்கு விசை

எடுத்துக்காட்டு 3.22 

0.25 kg நிறையுடைய கல் ஒன்று கயிற்றின் முனையில் கட்டப்பட்டு 2 m s-1 வேகத்தில் 3 m ஆரமுடைய சீரானவட்ட இயக்கத்தை மேற்கொள்கிறது. கல்லின் மீது செயல்படும் இழுவிசையினைக் கண்டுபிடி 

தீர்வு:

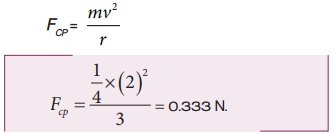
எடுத்துக்காட்டு 3.23 

நிலா, புவியினை வட்டப்பாதைக்கு ஒத்த ஒரு பாதையில் 27.3 நாட்களில் முழுமையாகச் சுற்றி வருகிறது. புவியின் ஆரம் 6.4 × 106 m எனில் நிலாவின் மீது செயல்படும் மையநோக்கு முடுக்கத்தைக் காண்க. 

தீர்வு 

மையநோக்கு முடுக்கம் a = v2/r. இச் சமன்பாடு வெளிப்படையாகவே நிலவின் வேகத்தைச் சார்ந்தது. இந்த வேகத்தை கணக்கிடுவது சற்றுக் கடினமாகும். எனவே நாம் பின்வரும் சமன்பாட்டினைப் பயன்படுத்தலாம்.

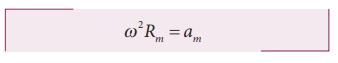
இங்கு am என்பது புவியின் ஈர்ப்பு விசையினால், நிலா பெறும் மைய நோக்கு முடுக்கமாகும். 

ω என்பது கோணத் திசைவேகம் 

Rm என்பது புவியிலிருந்து நிலா வரை உள்ள தொலைவு. இது புவியின் ஆரத்தைப் போன்று 60 மடங்காகும்.

புவியை நோக்கி நிலாவின் மையநோக்கு முடுக்கம் 0.00272 m s-2

இந்தக் கணக்கீடு நியூட்டனாலேயே செய்யப்பட்டதாகும். இம்முடிவினை நாம் பிற்பகுதியில் கற்கவுள்ள அலகு 6 இல் பயன்படுத்துவோம்.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் சரி சமமான வட்டச் சாலையில் செல்லும் வாகனம்

எடுத்துக்காட்டு 3.24 

ஆரம் 10 m மற்றும் நிலை உராய்வுக் குணகம் 0.81 கொண்ட சரிசமமான வட்டவடிவச் சாலை ஒன்றைக் கருதுக. அச்சாலையில் மூன்று கார்கள் (A,B மற்றும் C) முறையே 7 m s-1, 8 m s-1 , 10 m s-1 வேகத்தில் செல்கின்றன. இவற்றுள் எந்த கார் வட்ட வடிவச்சாலையில் செல்லும் போது சறுக்கி விழும்? (g = 10 m s-2) 

தீர்வு 

சரி சமமான வட்டச்சாலையில் செல்லும் வாகனம் சறுக்காமல் இருக்கத் தேவையான நிபந்தனை, வாகனத்தின் வேகம் (v) இன் மதிப்பு 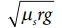ஐ விடக் குறைவாகவோ அல்லது சமமாகவோ இருக்க வேண்டும்.

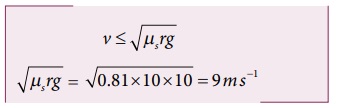
C காரினைப் பொருத்தவரை 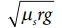இன் மதிப்பு காரின் வேகம் v ஐ விடக் குறைவு. கார் A மற்றும் B இரண்டும் பாதுகாப்பாக வளையும், ஆனால் கார் C இன் வேகம், நிர்ணயிக்கப்பட்ட வேகத்தை விட (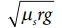) அதிகமாக உள்ளதால் அது சறுக்கி விடும்.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் வெளிவிளிம்பு உயர்த்தப்பட்ட சாலை

எடுத்துக்காட்டு 3.25 

20 m ஆரமுடைய வட்டச்சாலையைக் கருதுக. அதன் வெளிவிளிம்புக் கோணம் 15°என்க. அச்சாலையில் செல்லும் வாகனம் நழுவி விழாமல் பாதுகாப்பாக வளைவதற்குத் தேவையான வேகத்தைக் காண்க. 

தீர்வு

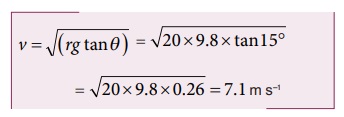
சறுக்கி விழாமல் பாதுகாப்பாக வளைவதற்குத் தேவையான வேகம் = 7.1 m s-1

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் புவியின் சுழற்சியால் ஏற்படும் மையவிலக்கு விசை

எடுத்துக்காட்டு 3.26 

சென்னையிலுள்ள 60 kg நிறையுடைய மனிதரின் மீது செயல்படும் மையவிலக்கு விசையைக் காண்க. 

(கொடுக்கப்பட்டவை: சென்னையில் குறுக்குக் கோடு θ = 13°) 

தீர்வு 

மையவிலக்கு விசை Fcf = mω2 R cosθ 

புவியின் கோணத் திசைவேகம்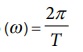

இங்கு T என்பது புவியின் அலைவு நேரம் (24 மணிநேரம்)

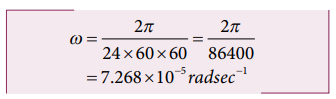
புவியின் ஆரம் R = 6400 km = 6400×103 m

சென்னையின் குறுக்கு கோடு (Latitude) = 13°

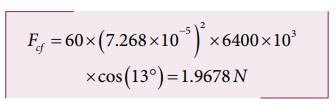
60 kg நிறையுடைய மனிதரொருவர் உணரும் மைய விலக்கு விசை தோராயமாக 2 நியூட்டனாகும். ஆனால் புவியின் ஈர்ப்பு விசையின் காரணமாக 60 kg நிறையுடைய அம்மனிதர் உணரும் விசை = mg = 60 × 9.8 = 588 N. இந்த விசைமையவிலக்கு விசையை விட மிக அதிகம்.