11 Я«хЯ«цЯ»Ђ Я«хЯ»ЄЯ«цЯ«┐Я«»Я«┐Я«»Я«▓Я»Ї : Я«ЁЯ«▓Я«ЋЯ»Ђ 1 : Я«хЯ»ЄЯ«цЯ«┐Я«»Я«┐Я«»Я«▓Я«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ»ЄЯ«цЯ«┐Я«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї
Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї
1. Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї
Я«њЯ«░Я»Ђ Я«џЯ»ЄЯ«░Я»ЇЯ««Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«ЁЯ«БЯ»ЂЯ«хЯ«┐Я«ЕЯ»Ї Я«єЯ«ЋЯ»ЇЯ«ИЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ, Я«ЁЯ«хЯ»ЇЯ«хЯ«БЯ»ЂЯ«хЯ«┐Я«ЕЯ»ѕЯ«цЯ»Ї Я«цЯ«хЯ«┐Я«░Я»ЇЯ«цЯ»ЇЯ«цЯ»Ђ, Я«фЯ«┐Я«▒ Я«ЁЯ«БЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ѕ, Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«БЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«хЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«хЯ«┐Я«цЯ«┐Я«ЋЯ«│Я«┐Я«ЕЯ»ЇЯ«фЯ«ЪЯ«┐ Я«еЯ«┐Я«░Я»ЇЯ«БЯ«»Я««Я»Ї Я«џЯ»єЯ«»Я»ЇЯ«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ, Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«хЯ«┤Я«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«Е Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«▓Я»Ї, Я«ЁЯ«»Я«ЕЯ«┐Я«ЋЯ«│Я«ЙЯ«Ћ Я«еЯ»ђЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«» Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«░Я»Ї, Я«ЁЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«ЁЯ«БЯ»ЂЯ«хЯ«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ Я«јЯ«ъЯ»ЇЯ«џЯ«┐Я«»Я«┐Я«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЋЯ«▒Я»ЇЯ«фЯ«ЕЯ»ѕЯ«»Я«ЙЯ«Е Я««Я«┐Я«ЕЯ»ЇЯ«џЯ»ЂЯ««Я»ѕ Я«јЯ«Е Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я««Я«ЙЯ«▒Я»ЇЯ«▒Я«ЙЯ«Ћ Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«еЯ«┐Я«▓Я»ѕ Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«ЙЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«БЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«хЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«хЯ«┐Я«цЯ«┐Я«ЋЯ«│Я»Ї
1) Я«њЯ«░Я»Ђ Я«цЯ«ЕЯ«┐Я«цЯ»ЇЯ«ц Я«цЯ«ЕЯ«┐Я««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї (Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«хЯ»ЄЯ«▒Я»єЯ«еЯ»ЇЯ«ц Я«цЯ«ЕЯ«┐Я««Я«цЯ»ЇЯ«цЯ»ЂЯ«ЪЯ«ЕЯ»ЂЯ««Я»Ї Я«фЯ«┐Я«БЯ»ѕЯ«еЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ц Я«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«▓Я»Ї) Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї Я«фЯ»ѓЯ«юЯ»ЇЯ«»Я««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ :
H2, Cl2, Na, S8 Я«єЯ«ЋЯ«┐Я«»Я«ЕЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЁЯ«БЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї Я«фЯ»ѓЯ«юЯ»ЇЯ«»Я««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
2) Я«ЊЯ«░Я«БЯ»Ђ Я«ЁЯ«»Я«ЕЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«еЯ«┐Я«▓Я»ѕ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЁЯ«еЯ»ЇЯ«ц Я«ЁЯ«»Я«ЕЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«еЯ«┐Я«ЋЯ«░ Я««Я«┐Я«ЕЯ»ЇЯ«џЯ»ЂЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ««Я««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ :
Na+ Я«ЁЯ«»Я«ЕЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«џЯ»ІЯ«ЪЯ«┐Я«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї +1 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Cl- Я«ЁЯ«»Я«ЕЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»ЂЯ«│Я»ІЯ«░Я«┐Я«ЕЯ«┐Я«ЕЯ»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї -1
3) Я«њЯ«░Я»Ђ Я««Я»ѓЯ«▓Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«▒Я«┐Я«▓Я»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«БЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«фЯ»ѓЯ«юЯ»ЇЯ«»Я««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї, Я«ЁЯ«»Я«ЕЯ«┐Я«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ»іЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ«хЯ«░Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЄЯ«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я«ЙЯ«ЕЯ«цЯ»Ђ Я«ЁЯ«»Я«ЕЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«еЯ«┐Я«ЋЯ«░ Я««Я«┐Я«ЕЯ»ЇЯ«џЯ»ЂЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ««Я««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ :
H2SO4 Я«▓Я»Ї, (2 ├Ќ H - Я«ЕЯ»Ї Я«єЯ«џЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї) + (S - Я«ЕЯ»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї) + (4 ├Ќ Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ«┐Я«ЕЯ»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї) = 0
SO42- Я«▓Я»Ї (1 ├Ќ S-Я«ЕЯ»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї) + (4 ├Ќ O-Я«ЕЯ»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї) = -2
4) Я«ЅЯ«▓Я»ІЯ«Ћ Я«╣Я»ѕЯ«ЪЯ»ЇЯ«░Я»ѕЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ«хЯ«┐Я«░ Я«фЯ«┐Я«▒ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ«џЯ»Ї Я«џЯ»ЄЯ«░Я»ЇЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»ЂЯ««Я»Ї Я«╣Я»ѕЯ«ЪЯ»ЇЯ«░Я«юЯ«ЕЯ«┐Я«ЕЯ»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї +1, Я«ЅЯ«▓Я»ІЯ«Ћ Я«╣Я»ѕЯ«ЪЯ»ЇЯ«░Я»ѕЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«╣Я»ѕЯ«ЪЯ»ЇЯ«░Я«юЯ«ЕЯ»Ї -1 Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«еЯ«┐Я«▓Я»ѕЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ :
Я«╣Я»ѕЯ«ЪЯ»ЇЯ«░Я«юЯ«ЕЯ»Ї Я«ЋЯ»ЂЯ«│Я»ІЯ«░Я»ѕЯ«ЪЯ«┐Я«▓Я»Ї (HCl), Я«╣Я»ѕЯ«ЪЯ»ЇЯ«░Я«юЯ«ЕЯ«┐Я«ЕЯ»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї +1
Я«џЯ»ІЯ«ЪЯ«┐Я«»Я««Я»Ї Я«╣Я»ѕЯ«ЪЯ»ЇЯ«░Я»ѕЯ«ЪЯ«┐Я«▓Я»Ї (NaH), Я«╣Я»ѕЯ«ЪЯ»ЇЯ«░Я«юЯ«ЕЯ«┐Я«ЕЯ»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї -1
5) Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ«џЯ»Ї Я«џЯ»ЄЯ«░Я»ЇЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ѓЯ«░Я«┐Я«ЕЯ«ЙЯ«ЕЯ«цЯ»Ђ -1 Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
6) Я«фЯ»єЯ«░Я»ЂЯ««Я»ЇЯ«фЯ«ЙЯ«▓Я«ЙЯ«Е Я«џЯ»ЄЯ«░Я»ЇЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»Ї-2 Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«фЯ»єЯ«░Я«ЙЯ«ЋЯ»ЇЯ«ИЯ»ѕЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї, Я«џЯ»ѓЯ«фЯ»ЇЯ«фЯ«░Я»Ї Я«єЯ«ЋЯ»ЇЯ«ИЯ»ѕЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї, Я«фЯ»ЂЯ«│Я»ѓЯ«░Я«┐Я«ЕЯ«┐Я«ЕЯ»Ї Я«џЯ»ЄЯ«░Я»ЇЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ«┐Я«»Я«Е Я«ЄЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«хЯ«┐Я«цЯ«┐Я«хЯ«┐Я«▓Я«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї :
Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ«┐Я«ЕЯ»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї
i) Я«еЯ»ђЯ«░Я«┐Я«▓Я»Ї (H2O) - 2 [ 2 (+1) + x = 0; x = -2 ]
ii) Я«╣Я»ѕЯ«ЪЯ»ЇЯ«░Я«юЯ«ЕЯ»Ї Я«фЯ»єЯ«░Я«ЙЯ«ЋЯ»ЇЯ«ИЯ»ѕЯ«ЪЯ«┐Я«▓Я»Ї (H2O2)
H2O2
2 (+1) + 2x = 0;
РЄњ 2x = Рѕњ2 ;
РЄњ x = -1
iii) KO2 Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒ Я«џЯ»ѓЯ«фЯ»ЇЯ«фЯ«░Я»Ї Я«єЯ«ЋЯ»ЇЯ«ИЯ»ѕЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї
- (1/2)
+1 + 2x = 0;
2x = Рѕњ 1 ; x = - (1/2)
iv) Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»Ї Я«ЪЯ»ѕЯ«фЯ»ЂЯ«│Я»ѓЯ«░Я»ѕЯ«ЪЯ«┐Я«▓Я»Ї (OF2) + 2.
x + 2 (-1) = 0; x = + 2
7) Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ«џЯ»Ї Я«џЯ»ЄЯ«░Я»ЇЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»ЂЯ««Я»Ї, Я«ЋЯ«ЙЯ«░ Я«ЅЯ«▓Я»ІЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї +1 Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«ЕЯ»ѕЯ«»Я»ЂЯ««Я»Ї, Я«ЋЯ«ЙЯ«░Я««Я«БЯ»Ї Я«ЅЯ«▓Я»ІЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї +2 Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«ЕЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я»ЂЯ«│Я»ЇЯ«│Я«Е.
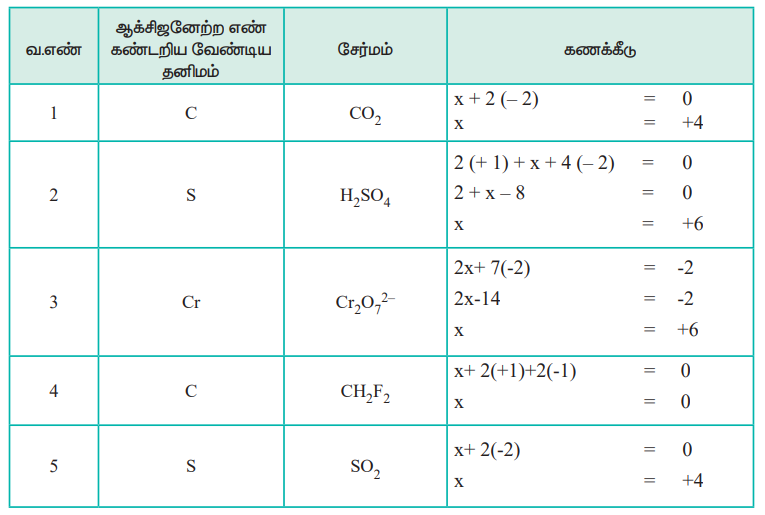
Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│ Я«хЯ«┐Я«цЯ«┐Я«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«БЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ЂЯ«цЯ«▓Я»Ї
Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ - Я«њЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ«┐Я«ЕЯ»ѕЯ«ЋЯ«│Я»Ї.
Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ - Я«њЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ«┐Я«ЕЯ»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»ІЯ«цЯ»Ђ, Я«цЯ«ЕЯ«┐Я««Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї Я««Я«ЙЯ«▒Я»ЇЯ«▒Я««Я«ЪЯ»ѕЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«њЯ«░Я»ЂЯ«хЯ«┐Я«ЕЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«цЯ«ЕЯ«┐Я««Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї Я«ЁЯ«цЯ«┐Я«ЋЯ«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«»Я«┐Я«ЕЯ»Ї Я«ЁЯ«хЯ»ЇЯ«хЯ«┐Я«ЕЯ»ѕ Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«хЯ«┐Я«ЕЯ»ѕ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї Я«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я»ЂЯ««Я«ЙЯ«»Я«┐Я«ЕЯ»Ї Я«ЁЯ«хЯ»ЇЯ«хЯ«┐Я«ЕЯ»ѕ Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»Ї Я«њЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ«┐Я«ЕЯ»ѕ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«хЯ«┐Я«ЕЯ»ѕЯ«»Я«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЂЯ«Ћ.
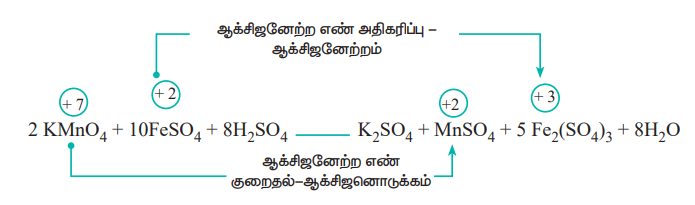
Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«ЕЯ»ѕЯ«»Я«┐Я«▓Я»Ї, Я«фЯ»іЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«џЯ«┐Я«»Я««Я»Ї Я«фЯ»єЯ«░Я»ЇЯ««Я«ЙЯ«ЎЯ»ЇЯ«ЋЯ«ЕЯ»ЄЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї (KMnO4) Я«ЅЯ«│Я»ЇЯ«│ Я««Я«ЙЯ«ЎЯ»ЇЯ«ЋЯ«ЕЯ»ђЯ«ИЯ»Ї (Mn), Я«фЯ»єЯ«░Я»ЇЯ«░Я«ИЯ»Ї Я«џЯ«▓Я»ЇЯ«фЯ»ЄЯ«ЪЯ»ЇЯ«ЪЯ»ѕ, (FeSO4) Я«фЯ»єЯ«░Я»ЇЯ«░Я«┐Я«ЋЯ»Ї Я«џЯ«▓Я»ЇЯ«фЯ»ЄЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ (Fe2(SO4)3) Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї Я«ЁЯ«ЪЯ»ѕЯ«»Я«џЯ»Ї Я«џЯ»єЯ«»Я»ЇЯ«хЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«ЋЯ«ЙЯ«░Я«БЯ««Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«хЯ»ЇЯ«хЯ«┐Я«ЕЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я««Я«ЙЯ«ЎЯ»ЇЯ«ЋЯ«ЕЯ»ђЯ«ИЯ»Ї Я«љЯ«еЯ»ЇЯ«цЯ»Ђ Я«јЯ«▓Я«ЋЯ»ЇЯ«ЪЯ»ЇЯ«░Я«ЙЯ«ЕЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЈЯ«▒Я»ЇЯ«▒Я»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«њЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ««Я«ЪЯ»ѕЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«цЯ»ЇЯ«цЯ«ЋЯ»ѕЯ«» Я«хЯ«┐Я«ЕЯ»ѕЯ«фЯ»ЇЯ«фЯ»іЯ«░Я»ЂЯ«ЪЯ»ЇЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒Я«┐Я«ЋЯ«│Я»Ї Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«ЄЯ«цЯ»ѕЯ«фЯ»ЇЯ«фЯ»ІЯ«▓Я«хЯ»Є, Я«јЯ«▓Я«ЋЯ»ЇЯ«ЪЯ»ЇЯ«░Я«ЙЯ«ЕЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЄЯ«┤Я«еЯ»ЇЯ«цЯ»Ђ Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»Ї Я«њЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«цЯ»ЂЯ«БЯ»ѕ Я«фЯ»ЂЯ«░Я«┐Я«»Я»ЂЯ««Я»Ї Я«хЯ«┐Я«ЕЯ»ѕЯ«фЯ»ЇЯ«фЯ»іЯ«░Я»ЂЯ«ЪЯ»ЇЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЇЯ«џЯ«┐Я«юЯ«ЕЯ»Ї Я«ЊЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЋЯ«│Я»Ї Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е.