வரையறை, தேற்றம், எடுத்துக்காட்டு கணக்குகள் - வெக்டரைக் கூறுகளாகப் பிரித்தல் (Resolution of Vectors) | 11th Mathematics : UNIT 8 : Vector Algebra I
11 வது கணக்கு : அலகு 8 : வெக்டர் இயற்கணிதம் (Vector Algebra)
வெக்டரைக் கூறுகளாகப் பிரித்தல் (Resolution of Vectors)
வெக்டரைக் கூறுகளாகப் பிரித்தல் (Resolution of Vectors)
ஒரு வெக்டரைக் கூறுகளாக எந்தவொரு முடிவுள்ள பரிமாணத்திலும் பிரிக்கலாம். ஆனால் நாம் இரண்டு மற்றும் மூன்று பரிமாணங்களில் கூறுகளாக பிரிப்பதைக் காணலாம்.
நாம் இப்பொழுது இரு பரிமாணத்தில் இருந்து தொடங்குவோம்.
1. இரு பரிமாணத்தில் ஒரு வெக்டரின் கூறுகள் (Resolution of a vector in two dimension)
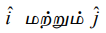 என்பவை முறையே x, y அச்சுகளின் மிகைத் திசையில் O−வை ஆரம்பப்புள்ளியாகக் கொண்ட ஓரலகு வெக்டர்கள் என்க. தளத்தில் P என்ற புள்ளியின் நிலை வெக்டர்
என்பவை முறையே x, y அச்சுகளின் மிகைத் திசையில் O−வை ஆரம்பப்புள்ளியாகக் கொண்ட ஓரலகு வெக்டர்கள் என்க. தளத்தில் P என்ற புள்ளியின் நிலை வெக்டர் ![]() எனில் அதனை x, y என்கிற ஒருமைத்தன்மை வாய்ந்த மெய்யெண்களுக்கு
எனில் அதனை x, y என்கிற ஒருமைத்தன்மை வாய்ந்த மெய்யெண்களுக்கு 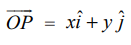 என எழுதலாம். மேலும்
என எழுதலாம். மேலும் 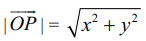
நிரூபணம்

முடிவு 8.8
ஒரு தளத்தில் ![]() ஆகியவை ஒரே கோட்டில் அமையாத இரு வெக்டர்கள் எனில், அந்தத் தளத்தில் உள்ள எந்தவொரு வெக்டரையும்
ஆகியவை ஒரே கோட்டில் அமையாத இரு வெக்டர்கள் எனில், அந்தத் தளத்தில் உள்ள எந்தவொரு வெக்டரையும் 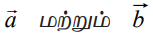 −ன் ஒருபடிச் சேர்க்கையாக ஒரே ஒரு வழியில் எழுத முடியும். அதாவது அத்தளத்தில் உள்ள எந்த ஒரு வெக்டரையும்
−ன் ஒருபடிச் சேர்க்கையாக ஒரே ஒரு வழியில் எழுத முடியும். அதாவது அத்தளத்தில் உள்ள எந்த ஒரு வெக்டரையும் 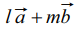 என எழுதலாம். இங்கு l மற்றும் m திசையிலிகள் ஆகும்.
என எழுதலாம். இங்கு l மற்றும் m திசையிலிகள் ஆகும்.
நிரூபணம்

குறிப்பு 8.2
ஏதேனும் மூன்று ஒரே நேர்க்கோட்டில் அமையாத வெக்டர்கள் ஒரு தள அமை வெக்டர்கள் எனில் இதில் எந்த ஒரு வெக்டரையும் மற்ற இரு வெக்டர்களின் ஒருபடிச் சேர்க்கையாக ஒரே வழியில் எழுதலாம். மேலும் இதன் மறுதலையும் உண்மையாகும்.
முடிவு 8.9
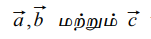 ஆகியவை ஒரே தளத்தில் அமையாத வெளியில் அமைந்த ஏதேனும் மூன்று வெக்டர்கள் எனில், வெளியில் அமைந்த எந்த ஒரு வெக்டரையும்
ஆகியவை ஒரே தளத்தில் அமையாத வெளியில் அமைந்த ஏதேனும் மூன்று வெக்டர்கள் எனில், வெளியில் அமைந்த எந்த ஒரு வெக்டரையும் 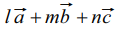 என எழுதலாம். இங்கு l, m மற்றும் n ஆகியவை திசையிலிகளாகும்.
என எழுதலாம். இங்கு l, m மற்றும் n ஆகியவை திசையிலிகளாகும்.
வரையறை 8.15
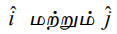 முறையே x மற்றும் y அச்சின் மிகைத் திசையில் அமைந்த அலகு வெக்டர்கள் என்க.
முறையே x மற்றும் y அச்சின் மிகைத் திசையில் அமைந்த அலகு வெக்டர்கள் என்க. ![]() என்பது இத்தளத்தில் உள்ள ஏதேனும் ஒரு வெக்டர் எனில்,
என்பது இத்தளத்தில் உள்ள ஏதேனும் ஒரு வெக்டர் எனில், 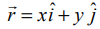 ஆகும். இங்கு x மற்றும் y மெய்யெண்கள். இங்கு
ஆகும். இங்கு x மற்றும் y மெய்யெண்கள். இங்கு 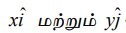 ஆகியவை முறையே x மற்றும் y அச்சின் திசையில்
ஆகியவை முறையே x மற்றும் y அச்சின் திசையில் ![]() −ன் இருபரிமாணக் கூறுகள் ஆகும்.
−ன் இருபரிமாணக் கூறுகள் ஆகும்.
நாம் இதுவரை இரு பரிமாணத்தில் விவாதித்த கூறுகளை முப்பரிமாண வெளிக்கும் விரிவுபடுத்தலாம்.
2. முப்பரிமாண வெளியில் ஒரு வெக்டரின் கூறுகள் (Resolution of a vector in three dimension)
தேற்றம் 8.6
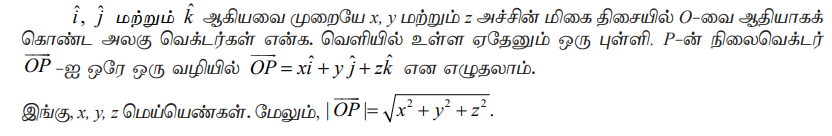
நிரூபணம்
P−ன் ஆயத்தொலைகள் (x, y, z) என்க. P−லிருந்து xy−தளத்திற்கு வரையப்பட்ட செங்குத்தின் அடிப்புள்ளி Q என்க. R மற்றும் S ஆகியவை Qவிலிருந்து முறையே x மற்றும் y−அச்சுகளுக்கு வரையப்பட்ட செங்குத்தின் அடிப்புள்ளிகள். 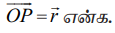
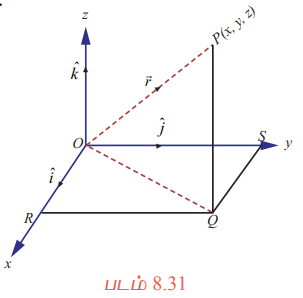
அப்பொழுது OR = x, OS = y, QP = z.
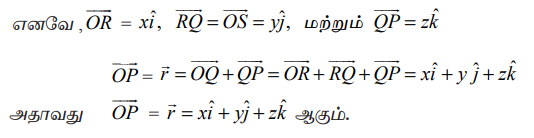
இதுவே O−வைப் பொறுத்த முப்பரிமாண வெளியில் P−ன் நிலை வெக்டர் ஆகும். முக்கோணம் ORQ−ல்
OQ2 = OR2 + RQ2 (எவ்வாறு?)
மற்றும் முக்கோணம் OQP−ல்
OP2 = OQ2 +QP2.
OP2 = OQ2 + QP2 = OR2 + RQ2 + QP2 = x2 + y2 + z2

இரண்டு புள்ளிகளை இணைக்கும் வெக்டரின் கூறுகள் (Components of vector joining two points)

3. ஒரு வெக்டரின் அணி வடிவம் (Matrix representation of a vector)
மூன்று கூறுகளைக் கொண்ட வெக்டரை ஒரு நிரை அணியாகவோ அல்லது நிரல் அணியாகவோ முறையே [x, y, z] அல்லது ![]() என எழுதலாம்.
என எழுதலாம்.
ஆகவே எந்தவொரு வெக்டர் 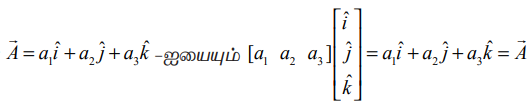 எனப் பெறலாம்.
எனப் பெறலாம்.
எனவே வெக்டர்களின் கூட்டல் மற்றும் திசையிலிப் பெருக்கல் ஆகியவை கீழ்க்காணுமாறு வரையறுக்கப்படுகிறது.
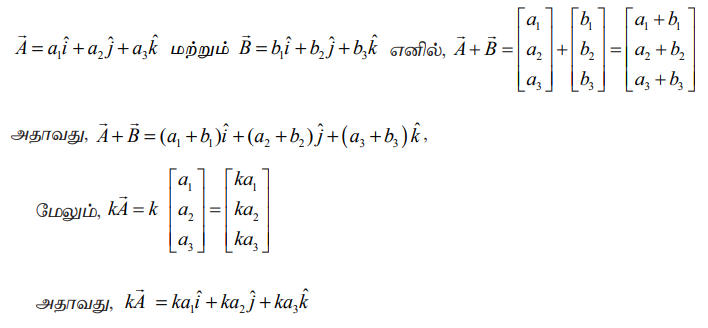
k ∈ ℝ க்கு k > 1 எனில், நீட்சியும், 0 < k < 1 எனில், குறுக்கமும், மேலும் k = 0 எனில், 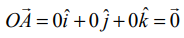 என பூஜ்ஜிய வெக்டரும் கிடைக்கும்.
என பூஜ்ஜிய வெக்டரும் கிடைக்கும்.
முடிவு 8.10
வெக்டர் கூட்டலின் பரிமாற்று மற்றும் சேர்ப்புப் பண்புகள், மற்றும் திசையிலி பெருக்கத்தின் பங்கீட்டு விதி ஆகியவற்றைப் பயன்படுத்தி கீழ்க்காண்பவைகளை நிறுவலாம்.
