Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї, Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ РђЊ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ, Я«ЄЯ«џЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ, Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ, Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЄЯ«џЯ»ѕЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«ЋЯ«│Я»Ї | Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ, Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я««Я»Ї, Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ«БЯ«Ћ№┐ - Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї | 11th Mathematics : UNIT 5 : Binomial Theorem, Sequences and Series
11Я«хЯ«цЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 5 : Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї, Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї
Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї
Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї (Finite Sequences)
Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я«▓Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«хЯ«░Я«┐Я«џЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ«хЯ«цЯ»Ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«џЯ»Ї Я«џЯ«┐Я«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ, a1, a2,Рђд Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«еЯ»ЄЯ«░Я«┐Я«ЪЯ»ѕЯ«»Я«ЙЯ«ЕЯ«цЯ»Ђ. Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕ Я«њЯ«░Я»Ђ Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«ЙЯ«Ћ Я«ЋЯ«░Я»ЂЯ«ц, Я«ЁЯ«цЯ«ЕЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«ЋЯ««Я»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЄЯ«»Я«▓Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«БЯ««Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ РёЋ Я«єЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«цЯ«фЯ»Ї Я«фЯ«ЙЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐ Я««Я»ЂЯ«┤Я»ЂЯ«хЯ«цЯ»ЂЯ««Я»Ї Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»ѕ Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Є Я«ЋЯ«ЙЯ«БЯ»ЇЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї. Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ«▓Я«ЙЯ««Я»Ї. Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«┐Я«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐ (AP) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«┐Я«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐ (GP) Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«цЯ«фЯ»Ї Я«фЯ«┐Я«░Я«┐Я«хЯ«┐Я«▓Я»Ї Я««Я»ЂЯ«ЕЯ»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«фЯ«ЪЯ«┐Я«цЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕЯ«ЋЯ«│Я»Ї, Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї.
┬и X Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«ЋЯ«БЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї n Рѕѕ РёЋ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, f : {1, 2, 3, . . . , n} Рєњ X Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»Ђ, X-Я«ЕЯ»Ї Я««Я»ђЯ«цЯ«ЙЯ«Е Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. g : РёЋРєњ X Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»Ђ, X-Я«ЕЯ»Ї Я««Я»ђЯ«цЯ«ЙЯ«Е Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. n Я«ЄЯ«▓Я»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»Ђ f -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ f(n) Я«љ an Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї. Я«ЁЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ (an) Я«јЯ«Е Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
┬и X Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ«БЯ««Я»Ї Я««Я»єЯ«»Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«БЯ««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЁЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«њЯ«░Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
┬и Я«јЯ«▓Я»ЇЯ«▓Я«Й Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»ЂЯ««Я»Ї, Я«јЯ«▓Я»ЇЯ«▓Я«ЙЯ«џЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«» Я«ЁЯ«хЯ«џЯ«┐Я«»Я««Я«┐Я«▓Я»ЇЯ«▓Я»ѕ.
┬и Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ђЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ«░Я«ЙЯ««Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ»ѕ Я«ЁЯ«▒Я«┐Я«хЯ»ІЯ««Я»Ї. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Я«њЯ«░Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ђЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я««Я»ђЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ«░Я«▓Я«ЙЯ««Я»Ї. Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«Ћ,
Я«њЯ«░Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я«џЯ««Я««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЁЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
┬и Я«њЯ«░Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ (an) -Я«љ Я«фЯ«ЪЯ««Я«ЙЯ«ЋЯ«цЯ»Ї Я«цЯ»єЯ«░Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»іЯ«│Я»ЇЯ«│ {(n, an) : n Рѕѕ РёЋ} Я«ЄЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«хЯ«░Я»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕ Я«хЯ«░Я»ѕЯ«цЯ«▓Я»Ї Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«» Я«џЯ«┐Я«▓ Я«хЯ«┐Я«хЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
1. Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї (Arithmetic and Geometric Progressions)
Я«џЯ«┐Я«▓ Я«џЯ«┐Я«▒Я«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї, Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«хЯ«┐Я«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ, Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЈЯ«▒Я»ЂЯ««Я»ЂЯ«ЋЯ««Я«ЙЯ«ЋЯ«хЯ»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«ЄЯ«▒Я«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЂЯ«ЋЯ««Я«ЙЯ«ЋЯ«хЯ»І Я«ЁЯ««Я»ѕЯ«»Я«▓Я«ЙЯ««Я»Ї.
Я«еЯ«ЙЯ««Я»Ї Я««Я»ЂЯ«ЕЯ»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«фЯ«ЪЯ«┐Я«цЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї, Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ»Ђ Я«ЋЯ»ѓЯ«░Я»ЇЯ«хЯ»ІЯ««Я»Ї.
Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ (Arithmetic Progression)(AP)
┬и a, a + d, a + 2d, a + 3d,..., a + (n - 1)d, a + nd,.... Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ, Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«хЯ«┐Я«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ (Arithmetic Progression) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ, Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ a Я«цЯ«хЯ«┐Я«░, Я««Я«▒Я»ЇЯ«▒ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я»ЂЯ«еЯ»ЇЯ«цЯ»ѕЯ«» Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЪЯ«ЕЯ»Ї Я«њЯ«░Я»Ђ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«»Я»ѕ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ, Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ d Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ««Я»Ї Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї a Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
┬и Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї n Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Tn = a + (n - 1)d.
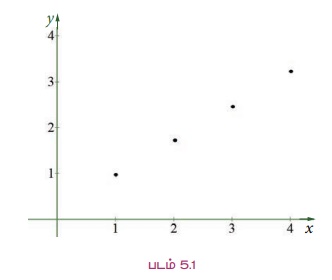
┬и 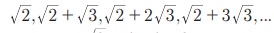 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 12, 9, 6, 3, Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї, Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є Рѕџ3 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї -3 Я«љ Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я«ЅЯ«ЪЯ»ѕЯ«» Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 12, 9, 6, 3, Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї, Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є Рѕџ3 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї -3 Я«љ Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я«ЅЯ«ЪЯ»ѕЯ«» Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
┬и 3, 7, 11 Я«єЯ«ЋЯ«┐Я«» Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«фЯ«ЋЯ«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ѕ Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е.
┬и a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«ЋЯ«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Tn = an + b,n Рѕѕ РёЋ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«▒Я»ЇЯ«▒ Я«фЯ«ЋЯ«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ«ЋЯ»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї.
Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ (Geometric Progression) (GP)
┬и a, ar, ar2, ar3,..., arn-1, arn,... a РЅа 0, r РЅа 0, Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ, Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«┐Я«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ (Geometric Progression) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ a Я«цЯ«хЯ«┐Я«░, Я««Я«▒Я»ЇЯ«▒ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«еЯ»ЇЯ«цЯ»ѕЯ«» Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕ Я«њЯ«░Я»Ђ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«»Я«ЙЯ«▓Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ r Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ, Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї a Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
┬и Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї n Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Tn = arn -1
┬и 1, 2, 4, 8, 16 .... Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 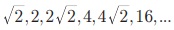 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї, Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є 2 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Рѕџ2 Я«љ Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я«ЅЯ«ЪЯ»ѕЯ«» Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї, Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є 2 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Рѕџ2 Я«љ Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я«ЅЯ«ЪЯ»ѕЯ«» Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
┬и Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї Я««Я«┐Я«ЋЯ»ѕ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї, Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ»ѕ Я«ЋЯ«ЙЯ«Б Я«ЁЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«Ћ Я««Я«ЙЯ«▒Я»ЂЯ««Я»Ї. a, ar, ar2,.... r > 0 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, log a, log(ar), log(ar2), ... Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ logr Я«љ Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ««Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
c РЅа 0 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, c, c, c,.... Я«јЯ«ЕЯ»ЇЯ«▒ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»ѕ Я«ЁЯ«▒Я«┐Я«»Я«▓Я«ЙЯ««Я»Ї.
0, 0, 0, Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ«┐Я«▒Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї. Я«ЄЯ«цЯ»ѕ Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«Ћ Я«ЁЯ«▒Я«┐Я«»Я«▓Я«ЙЯ««Я»Ї. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«цЯ»ѕ Я«њЯ«░Я»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«Ћ Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ a Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ 0 Я«єЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«ЁЯ«цЯ«ЕЯ»Ї Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«ЕЯ«хЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї? 1, 2 Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«хЯ»ЄЯ«▒Я»Ђ Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«јЯ«БЯ»Ї Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї, Я«еЯ«ЙЯ««Я»Ї Я«ЁЯ«цЯ»Є Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕ 0, 0, 0, Я«фЯ»єЯ«▒ Я««Я»ЂЯ«ЪЯ«┐Я«»Я»ЂЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ, Я«ЄЯ«еЯ»ЇЯ«ц Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї Я«јЯ«БЯ»ЇЯ«БЯ«▒Я»ЇЯ«▒Я«цЯ«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«ЄЯ«еЯ»ЇЯ«цЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«┤Я«фЯ»ЇЯ«фЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«цЯ»Ї Я«цЯ«хЯ«┐Я«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»Є Я«ЋЯ«БЯ«┐Я«цЯ«хЯ«┐Я«»Я«▓Я«ЙЯ«│Я«░Я»ЇЯ«ЋЯ«│Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї a РЅа 0 Я«јЯ«Е Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«ЋЯ«┐Я«▒Я«ЙЯ«░Я»ЇЯ«ЋЯ«│Я»Ї.
2 Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ РђЊ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ (Arithmetico- Geometric Progression) (AGP)
Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ»ЄЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ»Ђ Я«њЯ«░Я»Ђ Я«фЯ»ЂЯ«цЯ«┐Я«» Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЁЯ«цЯ»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ-Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«хЯ«┐Я«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ-Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕ AP Я«јЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕ GP Я«јЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ»ІЯ«▓Я»Ї Я«ЄЯ«еЯ»ЇЯ«ц Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕ AGP Я«јЯ«Е Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ«▓Я«ЙЯ««Я»Ї. Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«цЯ«ЋЯ«хЯ«┐Я«»Я«▓Я«┐Я«▓Я»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ«фЯ«ЙЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ«хЯ»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ«▓Я»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»ЂЯ««Я»Ї AGP-Я«ЕЯ»Ї Я«цЯ»ЄЯ«хЯ»ѕ Я«ЅЯ«БЯ«░Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ 5.1:
a,(a+d)r,(a + 2d)r2,(a + 3d)r3....(a +(n-1)d)rn-1,(a + nd)rn,.... Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ-Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«хЯ«┐Я«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ-Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ (Arithmetico-Geometric Progression) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
AP:a,a + d, a + 2d, ... Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї GP:1,r,r2,.... Я«јЯ«ЕЯ«┐Я«▓Я»Ї, a,(a+d)r,(a + 2d)r2, ... Я«јЯ«ЕЯ»ЇЯ«ф Я«цЯ»Ђ AGP Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц AGP-Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ a, Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ««Я»Ї d Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї r. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ, r = 1 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, AGP, AP Я«єЯ«ЋЯ«хЯ»ЂЯ««Я»Ї d = 0 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, AGP, GP Я«єЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я««Я«ЙЯ«▒Я»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я«џЯ«┐Я«▓ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«еЯ«┐Я«▓Я»ѕЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ Я«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«фЯ»іЯ«цЯ»ЂЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я«еЯ«┐Я«▓Я»ѕ Я«јЯ«ЕЯ«▓Я«ЙЯ««Я»Ї. AGP-Я«ЕЯ»Ї n Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Tn = (a +(n - 1)d)rn-1. Я«јЯ«▓Я»ЇЯ«▓Я«Й Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»ѕ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ»ѓЯ«▒Я«▓Я«ЙЯ««Я»Ї. Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, AP Я«љ 0, 1, 2, 3, 4, Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї, GP Я«љ 1, 1/2, 1/4, 1/8,.... Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї, AGP Я«љ 0/1, 1/2, 2/4, 3/8,... Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
4, 14, 40, 104, 256, 608 Рђд Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї a=4, d=3 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї r=2.
3. Я«ЄЯ«џЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ (Harmonic progression)
Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я««Я«ЙЯ«Е Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЄЯ«џЯ»ѕЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я«хЯ«┐Я«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«ЄЯ«џЯ»ѕЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ІЯ«ЪЯ»Ђ Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«» Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ»Ђ. Я«ЄЯ«џЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ Я«фЯ«▓ Я«ЄЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ 5.2:
h1, h2, h3, ... Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«њЯ«░Я»Ђ Я«ЄЯ«џЯ»ѕЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«Ћ (Harmonic Progression) 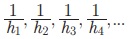 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.
Я«њЯ«░Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«ЄЯ«џЯ»ѕЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ«▓Я»ѕЯ«ЋЯ»ђЯ«┤Я«┐Я«ЋЯ«│Я»Ї Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«јЯ«Е Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«│Я«▓Я«ЙЯ««Я»Ї. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї, Я«ЄЯ«џЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»ѕ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«цЯ«▓Я»ѕЯ«ЋЯ»ђЯ«┤Я«┐Я«ЋЯ«│Я»Ї Я«јЯ«Е Я«ЋЯ»ѓЯ«▒ Я««Я»ЂЯ«ЪЯ«┐Я«»Я«ЙЯ«цЯ»Ђ. Я«ЈЯ«ЕЯ»єЯ«ЕЯ«┐Я«▓Я»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я««Я»Ї Я«њЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«цЯ«ЕЯ»Ї Я«цЯ«▓Я»ѕЯ«ЋЯ»ђЯ«┤Я«┐ Я«ЁЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ««Я»ЂЯ«│Я»ЇЯ«│Я«цЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«цЯ»Ђ. Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я««Я»Ї Я«њЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«ЙЯ«Ћ Я«ЄЯ«▓Я»ЇЯ«▓Я»ѕЯ«»Я»єЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«цЯ«ЕЯ»Ї Я«цЯ«▓Я»ѕЯ«ЋЯ»ђЯ«┤Я«┐Я«ЋЯ«│Я»Ї Я«њЯ«░Я»Ђ Я«ЄЯ«џЯ»ѕЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є, 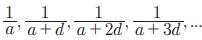 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЄЯ«џЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЪЯ«┐Я«хЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«њЯ«░Я»Ђ Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЂЯ«цЯ«┐ Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я««Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я««Я»ЂЯ«ЪЯ«┐Я«»Я«ЙЯ«цЯ»Ђ. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, a + kd РЅа 0; k Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я«▒Я»ЇЯ«▒ Я««Я»ЂЯ«┤Я»ЂЯ«јЯ«БЯ»Ї Я«јЯ«ЕЯ«хЯ»Є, -a/d Я«њЯ«░Я»Ђ Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»Ї Я«ЄЯ«▓Я»ЇЯ«▓Я»ѕ Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«┐Я«цЯ«┐ Я«ЁЯ«хЯ«џЯ«┐Я«»Я««Я»Ї. Я«ЄЯ«џЯ»ѕЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я«ЙЯ«Ћ Я««Я«ЙЯ«▒Я»ЇЯ«▒Я«┐ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я««Я»ѓЯ«▓Я««Я»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЄЯ«џЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЪЯ«┐Я«хЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«њЯ«░Я»Ђ Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЂЯ«цЯ«┐ Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я««Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я««Я»ЂЯ«ЪЯ«┐Я«»Я«ЙЯ«цЯ»Ђ. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, a + kd РЅа 0; k Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я«▒Я»ЇЯ«▒ Я««Я»ЂЯ«┤Я»ЂЯ«јЯ«БЯ»Ї Я«јЯ«ЕЯ«хЯ»Є, -a/d Я«њЯ«░Я»Ђ Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»Ї Я«ЄЯ«▓Я»ЇЯ«▓Я»ѕ Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«┐Я«цЯ«┐ Я«ЁЯ«хЯ«џЯ«┐Я«»Я««Я»Ї. Я«ЄЯ«џЯ»ѕЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я«ЙЯ«Ћ Я««Я«ЙЯ«▒Я»ЇЯ«▒Я«┐ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я««Я»ѓЯ«▓Я««Я»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ:
(i) Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ 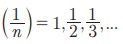 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЄЯ«џЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ. Я«еЯ«ЙЯ««Я»Ї,
Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЄЯ«џЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ. Я«еЯ«ЙЯ««Я»Ї, 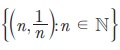 Я«хЯ«░Я»ѕЯ«фЯ«ЪЯ««Я»Ї Я«хЯ«░Я»ѕЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЄЯ«џЯ»ѕЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ (1/n) Я«љ Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«џЯ«┐Я«»Я«ЙЯ«Ћ Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
Я«хЯ«░Я»ѕЯ«фЯ«ЪЯ««Я»Ї Я«хЯ«░Я»ѕЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЄЯ«џЯ»ѕЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ (1/n) Я«љ Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«џЯ«┐Я«»Я«ЙЯ«Ћ Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
(ii) a, b, c Я«јЯ«ЕЯ»ЇЯ«фЯ«Е HP Я«јЯ«ЕЯ«┐Я«▓Я»Ї, 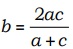 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(iii) Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї AP Я«ЄЯ«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї HP Я«ЄЯ«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.12 a, b, c Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ Я«ЄЯ«џЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, a/c = a-b/b-c Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї, Я«ЄЯ«цЯ«ЕЯ»Ї Я««Я«▒Я»ЂЯ«цЯ«▓Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЅЯ«БЯ»ЇЯ««Я»ѕ Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
a, b, c Я«јЯ«ЕЯ»ЇЯ«фЯ«Е HP Я«ЄЯ«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї 1/a, 1/b, 1/c Я«јЯ«ЕЯ»ЇЯ«фЯ«Е AP Я«ЄЯ«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є, 2/b = 1/a + 1/c. Я«ЄЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«цЯ»Ђ, ab - ac = ac - bc.
Я«јЯ«ЕЯ«хЯ»Є, a(b-c) = c(a - b). Я«ЄЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«цЯ»Ђ a/c = a-b/b-c
Я««Я«▒Я»ЂЯ«цЯ«▓Я»ѕЯ«»Я«ЙЯ«Ћ, a/c = a-b/b-c Я«јЯ«ЕЯ«┐Я«▓Я»Ї, a(b-c) = c(a - b)
Я«ЄЯ«░Я»ЂЯ«фЯ»ЂЯ«▒Я««Я»ЂЯ««Я»Ї abc Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«Ћ 1/c РђЊ 1/b = 1/b РђЊ 1/a.
Я«јЯ«ЕЯ«хЯ»Є, 1/a, 1/b, 1/c Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї a, b, c Я«њЯ«░Я»Ђ Я«ЄЯ«џЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.13 Я«њЯ«░Я»Ђ Я«ЄЯ«џЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«љЯ«еЯ»ЇЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«њЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є 1/19 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 1/35 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«фЯ«ЕЯ»ЇЯ«ЕЯ«┐Я«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
(hn) Я«њЯ«░Я»Ђ Я«ЄЯ«џЯ»ѕЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ»ЇЯ«Ћ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї an = 1/hn Я«јЯ«ЕЯ»ЇЯ«Ћ.
(an) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї a5 = 19 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї a9 = 35
a + 4d =19, a + 8d = 35 Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ, a = 3 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї d = 4 Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї 12 Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ a12 = a + 11d = 47. Я«ЄЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЄЯ«џЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї 12 Я«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ 1/47 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«еЯ«ЙЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«Е Я«ЋЯ»ѓЯ«▒Я«▓Я«ЙЯ««Я»Ї?
Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«цЯ«хЯ«┐Я«░ Я««Я«▒Я»ЇЯ«▒ Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЄЯ«џЯ»ѕЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
4. Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ, Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЄЯ«џЯ»ѕЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«ЋЯ«│Я»Ї (Arithmetic, Geometric and Harmonic Means)
Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«еЯ«ЙЯ««Я»Ї Я«ЁЯ«▒Я«┐Я«хЯ»ІЯ««Я»Ї. Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я«┐Я«▓Я»Ї Я«фЯ«▓Я«хЯ«ЋЯ»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐, Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЄЯ«џЯ»ѕЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«џЯ«┐Я«▓ Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЄЯ«▓Я»ЇЯ«▓Я«ЙЯ««Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»ЂЯ««Я»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕЯ«ЋЯ«│Я»ѕ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐
Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ 5.3:
n Я«њЯ«░Я»Ђ Я««Я«┐Я«ЋЯ»ѕ Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ»ЇЯ«Ћ. a1, a2, a3,.... an Я«јЯ«ЕЯ»ЇЯ«фЯ«Е n Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ, a1, a2, a3,.... an Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ (Arithmetic Mean) 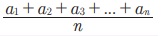 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
a1, a2, a3,.... an Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я«ЙЯ«ЋЯ«хЯ»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ«хЯ»І Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«» Я«ЁЯ«хЯ«џЯ«┐Я«»Я««Я«┐Я«▓Я»ЇЯ«▓Я»ѕ. 14, 14, 17, 20, 15 Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ 16 Я«јЯ«Е Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕЯ«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«јЯ«│Я«┐Я«цЯ«┐Я«▓Я»Ї Я«ЁЯ«▒Я«┐Я«»Я«▓Я«ЙЯ««Я»Ї. Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я«┐Я«▓Я»Ї, Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«▓Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї n Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«▓Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ«цЯ«┐Я«▓Я«ЙЯ«Ћ, Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї n Я«єЯ««Я»Ї Я«фЯ«ЪЯ«┐ Я««Я»ѓЯ«▓Я««Я»Ї Я«јЯ«Е Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ 5.4:
n Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я«▒Я»ЇЯ«▒ Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ»ЇЯ«Ћ. a1, a2, a3,.... an Я«јЯ«ЕЯ»ЇЯ«фЯ«Е n Я«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я«▒Я»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, 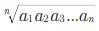 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ a1, a2, a3,.... an Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ (Geometric Mean) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ a1, a2, a3,.... an Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ (Geometric Mean) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ, a1, a2, a3,.... an Я«єЯ«ЋЯ«┐Я«» Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«хЯ»ЄЯ«▒Я»ЂЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«хЯ»ѕЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«» Я«ЁЯ«хЯ«џЯ«┐Я«»Я««Я«┐Я«▓Я»ЇЯ«▓Я»ѕ. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«хЯ»ѕ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я«▒Я»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«»Я«цЯ»Ђ Я«ЁЯ«хЯ«џЯ«┐Я«»Я««Я»Ї. 4, 6, 9 Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ 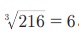 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. 4, 6, 9 Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐
Я«єЯ«ЋЯ»ЂЯ««Я»Ї. 4, 6, 9 Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ 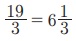 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕЯ«хЯ«┐Я«Ъ Я«ЁЯ«цЯ«┐Я«ЋЯ««Я«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ Я«јЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»ЂЯ««Я»Ї Я««Я»єЯ«»Я»ЇЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«Й?
Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕЯ«хЯ«┐Я«Ъ Я«ЁЯ«цЯ«┐Я«ЋЯ««Я«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ Я«јЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»ЂЯ««Я»Ї Я««Я»єЯ«»Я»ЇЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«Й?
Я«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я«▒Я»ЇЯ«▒ n Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐, Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕЯ«хЯ«┐Я«Ъ Я«ЁЯ«цЯ«┐Я«ЋЯ««Я«ЙЯ«Ћ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«џЯ««Я««Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«Е Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, AM Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕЯ«»Я»ЂЯ««Я»Ї, GM Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«цЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, AM РЅЦ GM Я«јЯ«ЕЯ«▓Я«ЙЯ««Я»Ї.
Я«еЯ«ЙЯ««Я»Ї Я«ЄЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ, AM РЅЦ GM Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ««Я«ЕЯ«┐Я«▓Я«┐Я«»Я»ѕ Я«ЄЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я«▒Я»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«еЯ«┐Я«▒Я»ЂЯ«хЯ«▓Я«ЙЯ««Я»Ї.
Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї 5.2
Я«ЄЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я«▒Я»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є AM Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї GM Я«јЯ«Е Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї, AM РЅЦ GM. Я«ЁЯ«еЯ»ЇЯ«ц Я«ЄЯ«░Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«џЯ««Я««Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ AM = GM Я«єЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я«▒Я»ЂЯ«цЯ«▓Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЅЯ«БЯ»ЇЯ««Я»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я«▒Я»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ 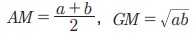 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(a + b)2 - 4ab = (a РђЊ b)2 РЅЦ 0. Я«ЁЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї, (a + b)2 - 4ab РЅЦ 0.
Я«ЄЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ, 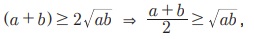
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ AM РЅЦ GM. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї,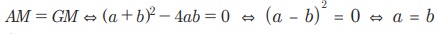 Я«јЯ«ЕЯ«хЯ»Є AM = GM Я«єЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є AM = GM Я«єЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
AM РЅЦ GM -Я«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«хЯ«ЪЯ«┐Я«х Я«ЋЯ«БЯ«┐Я«ц Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ««Я»Ї
a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я«▒Я»ЇЯ«▒ Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я»Ї Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я««Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї GM Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«Ћ Я«ЈЯ«цЯ»ЂЯ««Я«┐Я«▓Я»ЇЯ«▓Я»ѕ. Я«еЯ«ЙЯ««Я»Ї a > 0 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b > 0 Я«јЯ«Е Я«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї. a + b Я«еЯ»ђЯ«│Я««Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ AB Я«јЯ«ЕЯ»ЇЯ«▒ Я«њЯ«░Я»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«еЯ»ЇЯ«цЯ»Ђ, AB Я«љ Я«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ««Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«њЯ«░Я»Ђ Я«ЁЯ«░Я»ѕЯ«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«хЯ«░Я»ѕЯ«Ћ. M Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ AB -Я«ЕЯ»Ї Я«еЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«јЯ«ЕЯ«хЯ»Є, Я«ЁЯ«░Я»ѕЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ѕЯ«»Я««Я»Ї M Я«єЯ«ЋЯ»ЂЯ««Я»Ї. M Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ AB -Я«ЕЯ»Ї Я«еЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї,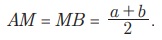
Я«јЯ«ЕЯ«хЯ»Є, Я«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«єЯ«░Я««Я»Ї ![]() Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
AD = a, DB = b Я«јЯ«ЕЯ»ЂЯ««Я«ЙЯ«▒Я»Ђ D Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕ AB-Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«Ћ.
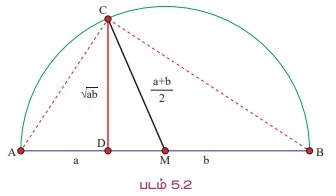
D Я«хЯ«┤Я«┐Я«»Я«ЙЯ«Ћ AB -Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»ІЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«Ћ. Я«ЁЯ«цЯ»Ђ Я«ЁЯ«░Я»ѕ Я«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ»ѕ C Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«Ћ. CA, CB Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї CM Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕ Я«хЯ«░Я»ѕЯ«Ћ. M Я«єЯ«ЕЯ«цЯ»Ђ Я«ЁЯ«░Я»ѕЯ«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ѕЯ«»Я««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї  Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ»єЯ«│Я«┐Я«хЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. ╬ћACD Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ╬ћCBD Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«њЯ«цЯ»ЇЯ«ц Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї,
Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ»єЯ«│Я«┐Я«хЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. ╬ћACD Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ╬ћCBD Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«њЯ«цЯ»ЇЯ«ц Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї,  Я«јЯ«ЕЯ«хЯ»Є, CD2 = AD ├Ќ BD = ab
Я«јЯ«ЕЯ«хЯ»Є, CD2 = AD ├Ќ BD = ab
Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, CD = Рѕџab (Я«фЯ«┐Я«цЯ«ЙЯ«ЋЯ«░Я«ИЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«»Я»ЂЯ««Я»Ї CD = Рѕџab Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ«▓Я«ЙЯ««Я»Ї.) Я«њЯ«░Я»Ђ Я«ЁЯ«░Я»ѕ Я«еЯ«ЙЯ«БЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї Я«јЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»ЂЯ««Я»Ї Я«єЯ«░Я«цЯ»ЇЯ«цЯ»ѕЯ«хЯ«┐Я«Ъ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«хЯ«ЙЯ«Ћ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«џЯ««Я««Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї, CD РЅц CM Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ 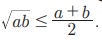 Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, AM РЅЦ GM.
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, AM РЅЦ GM.
D Я«єЯ«ЕЯ«цЯ»Ђ M-Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ Я«ЁЯ«░Я»ѕЯ«еЯ«ЙЯ«БЯ»Ї DC Я«єЯ«ЕЯ«цЯ»Ђ Я«єЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«џЯ««Я««Я«ЙЯ«Ћ Я««Я«ЙЯ«▒Я»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я«▒Я»ЂЯ«цЯ«▓Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЅЯ«БЯ»ЇЯ««Я»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, AM=GM Я«јЯ«ЕЯ«┐Я«▓Я»Ї, a = b Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї a = b Я«јЯ«ЕЯ«┐Я«▓Я»Ї AM =GM Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»Ђ 5.1 : a1, a2, a3, ..., an Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї, ak (k > 1) Я«јЯ«ЕЯ»ЇЯ«▒ Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я»ЂЯ«ЕЯ»ЇЯ«ЕЯ«┐Я«»Я«ЙЯ«Е ak-1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«┐Я«»Я«ЙЯ«Е ak+1 Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї a1, a2, a3, ..., an Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ««Я»Ї d Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ»ЇЯ«Ћ.
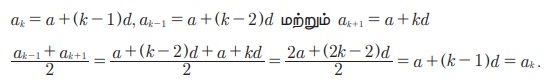
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, ak-1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ak+1 Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ ak Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»Ђ 5.2 : a1, a2, a3, ..., an Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«цЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ ak (k > 1), Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЕЯ»ЇЯ«ЕЯ«░Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я««Я»ЂЯ«ЕЯ»ЇЯ«ЕЯ«┐Я«»Я«ЙЯ«Е ak-1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«░Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«»Я«ЙЯ«Е ak+1 Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї a1, a2, a3, ..., an Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї r Я«ЅЯ«│Я»ЇЯ«│ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ»ЇЯ«Ћ.
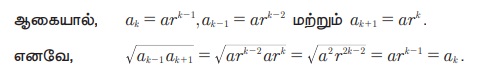
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, ak-1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ak+1 Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ ak Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.14 4, A1, A2, ..., A7, 7 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«▒Я»Ђ, A1, A2, ..., A7 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЈЯ«┤Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, 12, G1, G2, G3, G4, 3/8 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«▒Я»Ђ, G1, G2, G3, G4 Я«јЯ«ЕЯ»ЇЯ«▒ Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
a = 4 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 4 + 8d = 7. Я«ЄЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ, d = 3/8 Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е 7 Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї 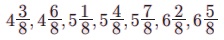 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, a = 12 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ar5 = 3/8 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї 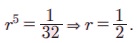 Я«јЯ«ЕЯ«хЯ»Є, Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е 4 Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї
Я«јЯ«ЕЯ«хЯ»Є, Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е 4 Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї 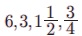 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.15 Я«њЯ«░Я»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї 4 Я«єЯ«хЯ«цЯ»Ђ, 5 Я«єЯ«хЯ«цЯ»Ђ, 6 Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї 4096 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 5 Я«єЯ«хЯ«цЯ»Ђ, 6 Я«єЯ«хЯ«цЯ»Ђ, 7 Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї 32768 Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЁЯ«еЯ»ЇЯ«ц Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї 8 Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЅЯ«ЪЯ»ѕЯ«» Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ a, ar, ar2,... Я«јЯ«ЕЯ»ЇЯ«Ћ.
4 Я«єЯ«хЯ«цЯ»Ђ, 5 Я«єЯ«хЯ«цЯ»Ђ, 6 Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є, ar3, ar4 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ar5 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▒Я»ЇЯ«фЯ«▓Я«ЕЯ»Ї, a3r12 = 4096. Я«ЄЯ«цЯ»Ђ Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ, a3r15 = 32768. Я«јЯ«ЕЯ«хЯ»Є, 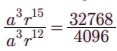
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, r3 = 8 РЄњ r = 2,
a3r12 = 4096, Я«ЄЯ«цЯ«┐Я«▓Я»Ї r = 2 Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ«┐Я«░Я«цЯ«┐Я«»Я«┐Я«Ъ, a3 = 1 РЄњ a = 1.
Я««Я»ЂЯ«цЯ«▓Я»Ї 8 Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 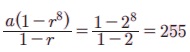 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«џЯ»ѕЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ (Harmonic Mean)
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЄЯ«џЯ»ѕЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЁЯ«еЯ»ЇЯ«ц Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ«▓Я»ѕЯ«ЋЯ»ђЯ«┤Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«цЯ«▓Я»ѕЯ«ЋЯ»ђЯ«┤Я«┐Я«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, h1, h2, ..., hn Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«цЯ«▓Я»ѕЯ«ЋЯ»ђЯ«┤Я«┐Я«ЋЯ«│Я»Ї 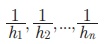 Я«јЯ«ЕЯ«хЯ»Є, Я«ЄЯ«цЯ»ЇЯ«цЯ«▓Я»ѕЯ«ЋЯ»ђЯ«┤Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐
Я«јЯ«ЕЯ«хЯ»Є, Я«ЄЯ«цЯ»ЇЯ«цЯ«▓Я»ѕЯ«ЋЯ»ђЯ«┤Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ 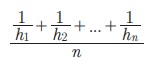 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«цЯ«▓Я»ѕЯ«ЋЯ»ђЯ«┤Я«┐
Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«цЯ«▓Я»ѕЯ«ЋЯ»ђЯ«┤Я«┐ 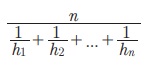 h1, h2, ..., hn Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЄЯ«џЯ»ѕЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
h1, h2, ..., hn Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЄЯ«џЯ»ѕЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ 5.5
{h1, h2, ..., hn} Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЄЯ«џЯ»ѕЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ 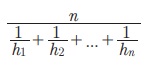 Я«јЯ«Е Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«јЯ«Е Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«Ћ, a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЄЯ«░Я»Ђ Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЄЯ«џЯ»ѕЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ 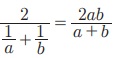
"n Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«јЯ«еЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЋЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї, Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«ЄЯ«џЯ»ѕЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕЯ«хЯ«┐Я«Ъ Я«ЁЯ«цЯ«┐Я«ЋЯ««Я«ЙЯ«ЋЯ«хЯ»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«џЯ««Я««Я«ЙЯ«ЋЯ«хЯ»І Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї" Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я«еЯ«┐Я«▒Я»ЂЯ«хЯ«▓Я«ЙЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, GM РЅЦ HM Я«ЄЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я«▒Я»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ, GM РЅЦ HM Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ««Я«ЕЯ«┐Я«▓Я«┐Я«»Я»ѕ Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї 5.3
Я«ЄЯ«░Я»Ђ Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЄЯ«џЯ»ѕЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є GM Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї HM Я«јЯ«Е Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я«ЙЯ«»Я«┐Я«ЕЯ»Ї, GM РЅЦ HM Я«јЯ«Е Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«еЯ»ЇЯ«ц Я«ЄЯ«░Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«џЯ««Я««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї GM = HM Я«єЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«цЯ«ЕЯ»Ї Я««Я«▒Я»ЂЯ«цЯ«▓Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЅЯ«БЯ»ЇЯ««Я»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«ЄЯ«░Я»Ђ Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ»ЇЯ«Ћ.

Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї 5.2 Я«ЄЯ«▓Я»Ї AM РЅЦ GM Я«јЯ«Е Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«цЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│Я»ІЯ««Я»Ї. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, Я«цЯ«▒Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ GM РЅЦ HM Я«јЯ«Е Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«цЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│Я»ІЯ««Я»Ї. Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЄЯ«БЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ AM РЅЦ GM РЅЦ HM Я«јЯ«Е Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»Ђ 5.3 : Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я»Ђ Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«ЋЯ«│Я»Ї AM, GM Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї HM Я«єЯ«ЋЯ«┐Я«» Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«ЄЯ«░Я»Ђ Я««Я«┐Я«ЋЯ»ѕ Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ»ЇЯ«Ћ.
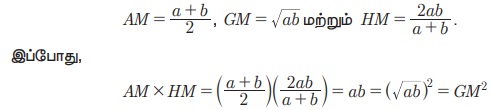
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, AM ├Ќ HM = GM2. Я«јЯ«ЕЯ«хЯ»Є, AM, GM Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї HM Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«њЯ«░Я»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«» Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
Рђб b Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї c-Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, a,b,c Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї
Рђб b Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї c-Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, a,b,c Я«њЯ«░Я»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Рђб b Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї c-Я«ЕЯ»Ї Я«ЄЯ«џЯ»ѕЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, a,b,c Я«њЯ«░Я»Ђ Я«ЄЯ«џЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«њЯ«░Я»Ђ Я«хЯ«ЙЯ«ЋЯ«ЕЯ««Я»Ї Я««Я«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ x Я«ЋЯ«┐Я««Я»ђ Я«хЯ»ЄЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«цЯ»ѓЯ«░Я««Я»Ї Я«фЯ«»Я«БЯ««Я»Ї Я«џЯ»єЯ«»Я»ЇЯ«цЯ»Ђ Я«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ»Ђ Я«цЯ«┐Я«░Я»ЂЯ««Я»ЇЯ«фЯ«┐ Я««Я«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ y Я«ЋЯ«┐Я««Я»ђ Я«хЯ»ЄЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«фЯ»ЂЯ«▒Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЄЯ«ЪЯ«цЯ»ЇЯ«цЯ»ѕ Я«хЯ«еЯ»ЇЯ«цЯ«ЪЯ»ѕЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«еЯ»ЇЯ«ц Я«хЯ«ЙЯ«ЋЯ«ЕЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ЂЯ«┤Я»Ђ Я«фЯ«»Я«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«хЯ»ЄЯ«ЋЯ««Я»Ї Я«ЄЯ«░Я»Ђ Я«хЯ»ЄЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЄЯ«џЯ»ѕЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЅЯ«БЯ»ЇЯ««Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«цЯ»ѓЯ«░Я««Я»Ї d Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«њЯ«░Я»ЂЯ«фЯ»ЂЯ«▒Я««Я»Ї Я«џЯ»єЯ«▓Я»ЇЯ«хЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«еЯ»ЄЯ«░Я««Я»Ї d/x Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я«▒Я»ЂЯ«фЯ»ЂЯ«▒Я««Я»Ї Я«хЯ«░Я»ЂЯ«хЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«еЯ»ЄЯ«░Я««Я»Ї d/y Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є, Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«хЯ»ЄЯ«ЋЯ««Я»Ї, 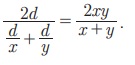
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, Я««Я«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ 60 Я«ЋЯ«┐Я««Я»ђ Я«хЯ»ЄЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«ЄЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕ Я«ЁЯ«ЪЯ»ѕЯ«еЯ»ЇЯ«цЯ»Ђ Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«░Я»Ї Я««Я«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ 40 Я«ЋЯ«┐Я««Я»ђ Я«хЯ»ЄЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«цЯ«┐Я«░Я»ЂЯ««Я»ЇЯ«ф Я«хЯ«еЯ»ЇЯ«цЯ«ЪЯ»ѕЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«еЯ»ЇЯ«ц Я«хЯ«ЙЯ«ЋЯ«ЕЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»іЯ«цЯ»ЇЯ«ц Я«фЯ«»Я«БЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«хЯ»ЄЯ«ЋЯ««Я»Ї 60 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 40-Я«ЕЯ»Ї Я«ЄЯ«џЯ»ѕЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, 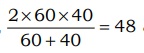 Я«ЋЯ«┐Я««Я»ђ/Я««Я«БЯ«┐ Я«хЯ»ЄЯ«ЋЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЋЯ«┐Я««Я»ђ/Я««Я«БЯ«┐ Я«хЯ»ЄЯ«ЋЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«фЯ«»Я«┐Я«▒Я»ЇЯ«џЯ«┐ 5.2
Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї n Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї 6 Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, Я«ЁЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї, Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ, Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ, Я«ЄЯ«џЯ»ѕЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ, Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ - Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я»Ї Я«јЯ«цЯ»ЂЯ«хЯ»ЂЯ««Я«┐Я«▓Я»ЇЯ«▓Я»ѕ Я«јЯ«Е Я«хЯ«ЋЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«Ћ.
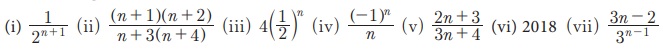
2. n - Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ an Я«љЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї 6 Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.

3. Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї n -Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.

4. Я«ЈЯ«▒Я»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї 5832. Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«јЯ«БЯ»ЇЯ«БЯ»ЂЯ«ЪЯ«ЕЯ»Ї 6 Я«љЯ«»Я»ЂЯ««Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«хЯ«цЯ»Ђ Я«јЯ«БЯ»ЇЯ«БЯ»ЂЯ«ЪЯ«ЕЯ»Ї 9 Я«љЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«ЁЯ«еЯ»ЇЯ«ц Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
5. 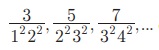 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї n Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕ Я«ЄЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ««Я«ЙЯ«Ћ Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ«Ћ.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї n Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕ Я«ЄЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ««Я«ЙЯ«Ћ Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ«Ћ.
6. Я«њЯ«░Я»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї k Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ tk Я«јЯ«ЕЯ«┐Я«▓Я»Ї, k -Я«ЕЯ»Ї Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я«┐Я«ЋЯ»ѕ Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї tn-k, tn, tn+k Я«јЯ«ЕЯ»ЇЯ«фЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
7. a,b,c Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«њЯ«░Я»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 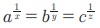 Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї, x, y, z Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї, x, y, z Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
8. Я«ЄЯ«░Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я«ЙЯ«ЕЯ«цЯ»Ђ, Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕ Я«хЯ«┐Я«Ъ 10 Я«ЁЯ«цЯ«┐Я«ЋЯ««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, Я«ЄЯ«џЯ»ѕЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕ Я«хЯ«┐Я«Ъ 16 Я«ЁЯ«цЯ«┐Я«ЋЯ««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЁЯ«еЯ»ЇЯ«ц Я«ЄЯ«░Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
9. (q-r)x2 + (r-p)x + p - q = 0 Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ««Я««Я«ЙЯ«ЕЯ«хЯ»ѕ Я«јЯ«ЕЯ«┐Я«▓Я»Ї p, q, r Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
10. Я«њЯ«░Я»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї p, q Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї r Я«єЯ«хЯ«цЯ»Ђ, Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є a, b Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї c Я«јЯ«ЕЯ«┐Я«▓Я»Ї, (q-r)loga + (r-p) log b + (p-q) log c = 0 Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.