Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»Ї | Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ, Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я««Я»Ї, Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»Ї, Я«фЯ«»Я«┐Я«▒Я»ЇЯ«џЯ«┐ | Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї - Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї | 11th Mathematics : UNIT 5 : Binomial Theorem, Sequences and Series
11Я«хЯ«цЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 5 : Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї, Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї
Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї
Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї (Binomial Theorem)
Я«ЄЯ«░Я»Ђ Я«џЯ«ЋЯ»ЇЯ«ЋЯ«░ Я«хЯ«ЙЯ«ЋЯ«ЕЯ««Я»Ї, Я«ЄЯ«░Я»Ђ Я«ЋЯ«БЯ»Ї Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐, Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЪЯ«┐Я««Я«ЙЯ«ЕЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»Ї Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»Ї Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, (1 + x), (x + y), (x2 + xy) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (2a + 3b) Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ«┐Я«▓ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
1. Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»Ї (Binomial Coefficients)
Я«фЯ«ЙЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐ 4-Я«ЄЯ«▓Я»Ї, nCr Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ««Я»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«ЋЯ«▒Я»ЇЯ«▒Я»ЂЯ«│Я»ЇЯ«│Я»ІЯ««Я»Ї Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ 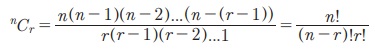 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«»Я»ЂЯ««Я»Ї Я«еЯ«ЙЯ««Я»Ї Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│Я»ІЯ««Я»Ї. nCr Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ, (1 + x)n Я«ЄЯ«▓Я»Ї xr -Я«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«хЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (a + b)n Я«ЄЯ«▓Я»Ї arbn-r -Я«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«хЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї, Я«ЄЯ«хЯ»ѕ Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»Ї (Binomial Coefficients) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. nCr -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я«ЋЯ«ЙЯ«Б Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«▓Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ»ѕЯ«хЯ«┐Я«Ъ Я«јЯ«│Я«┐Я««Я»ѕЯ«»Я«ЙЯ«Е Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»ЂЯ««Я»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«»Я»ЂЯ««Я»Ї Я«еЯ«ЙЯ««Я»Ї Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│Я»ІЯ««Я»Ї. nCr Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ, (1 + x)n Я«ЄЯ«▓Я»Ї xr -Я«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«хЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (a + b)n Я«ЄЯ«▓Я»Ї arbn-r -Я«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«хЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї, Я«ЄЯ«хЯ»ѕ Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»Ї (Binomial Coefficients) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. nCr -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я«ЋЯ«ЙЯ«Б Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«▓Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ»ѕЯ«хЯ«┐Я«Ъ Я«јЯ«│Я«┐Я««Я»ѕЯ«»Я«ЙЯ«Е Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»ЂЯ««Я»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
Я«фЯ«ЙЯ«ИЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї
Я«фЯ«ЙЯ«ИЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ nCr -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«Б Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ«цЯ«▓Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ (k + 1) Я«єЯ«хЯ«цЯ»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«ЙЯ«ЕЯ«цЯ»Ђ kC0, kC1, kC2, kC3,....,kCk Я«єЯ«ЋЯ«┐Я«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
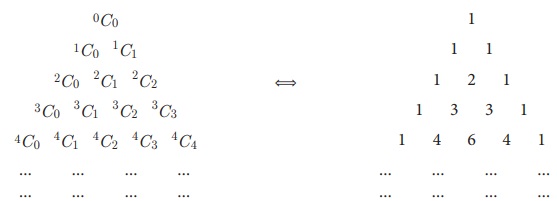
(a + b)0, (a + b)1, (a + b)2, (a + b)3 Я«јЯ«ЕЯ»ЇЯ«▒ Я««Я»ЂЯ«▒Я»ЇЯ«▒Я»іЯ«░Я»ЂЯ««Я»ѕЯ«ЋЯ«│Я»ѕ Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ»ЂЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЋЯ«хЯ«ЕЯ«┐Я«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я«ЁЯ«еЯ»ЇЯ«цЯ«ЋЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я»ЂЯ«▒Я»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
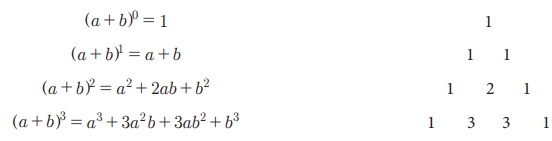
Я«фЯ«ЙЯ«ИЯ»ЇЯ«ЋЯ«▓Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ»ѕ Я«ЅЯ«▒Я»ЇЯ«▒Я»Ђ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ, Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«єЯ«░Я««Я»ЇЯ«фЯ««Я»ЂЯ««Я»Ї, Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ««Я»Ї 1 Я«єЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я«хЯ»ѕ Я««Я»ЂЯ«ЕЯ»Ї Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЄЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«Ъ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, '3' Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЕЯ»Ї Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ 1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 2-Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. 10 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»ЂЯ«ЕЯ»Ї Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї 10-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ««Я»ЄЯ«▓Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«ЄЯ«░Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї 4 Я««Я«▒Я»ЇЯ«▒Я««Я»Ї 6-Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
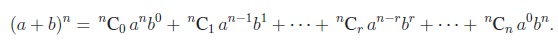 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ (a + b)n - Я«ЕЯ»Ї Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»ѕ Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«░Я»Ї Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї n-Я«ЕЯ»Ї Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї, (a + b)n -Я«ЕЯ»Ї Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕ Я«фЯ«ЙЯ«ИЯ»ЇЯ«ЋЯ«▓Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї. Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, Я«фЯ«ЙЯ«ИЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«љЯ«еЯ»ЇЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я»ѕ Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ (a + b)4 -Я«ЕЯ»Ї Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«»Я»ЂЯ««Я»Ї, Я«єЯ«▒Я«ЙЯ«хЯ«цЯ»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ (a + b)5 -Я«ЕЯ»Ї Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ (a + b)n - Я«ЕЯ»Ї Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»ѕ Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«░Я»Ї Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї n-Я«ЕЯ»Ї Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї, (a + b)n -Я«ЕЯ»Ї Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕ Я«фЯ«ЙЯ«ИЯ»ЇЯ«ЋЯ«▓Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї. Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, Я«фЯ«ЙЯ«ИЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«љЯ«еЯ»ЇЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я»ѕ Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ (a + b)4 -Я«ЕЯ»Ї Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«»Я»ЂЯ««Я»Ї, Я«єЯ«▒Я«ЙЯ«хЯ«цЯ»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ (a + b)5 -Я«ЕЯ»Ї Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
(a + b)5 -Я«ЕЯ»Ї Я«хЯ«┐Я«░Я«┐Я«хЯ«┐Я«▓Я»Ї, Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЄЯ«▓Я»ЇЯ«▓Я«ЙЯ««Я«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї
a5, a4b, a3b2, a2b3, ab4, b5
Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«фЯ«ЙЯ«ИЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї 6 Я«єЯ«хЯ«цЯ»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕ,
1 5 10 10 5 1 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«хЯ»ѕ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐,
(a + b)5 = a5, 5a4b, 10a3b2, 10a2b3 + 5ab4 + b5 Я«јЯ«Е Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї, Я«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я«ЄЯ«▓Я»ЇЯ«▓Я«ЙЯ««Я«▓Я»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«▓Я»ѕ Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Є Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«фЯ«ЙЯ«ИЯ»ЇЯ«ЋЯ«▓Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«јЯ«ЕЯ«хЯ»Є, (a + b)n, n Рѕѕ РёЋ Я«јЯ«ЕЯ»ЇЯ«▒ Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«хЯ«┐Я«░Я«┐Я«хЯ«┐Я«ЕЯ»ѕ Я«јЯ«еЯ»ЇЯ«ц Я«хЯ«┐Я«ц Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»ЂЯ««Я»Ї Я«ЄЯ«▓Я»ЇЯ«▓Я«ЙЯ««Я«▓Я»Ї Я«јЯ«┤Я»ЂЯ«ц Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї.
Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ«БЯ»ЇЯ«Ъ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«Б Я«хЯ«ЪЯ«┐Я«хЯ««Я»Ї, 17Я«єЯ««Я»Ї Я«еЯ»ѓЯ«▒Я»ЇЯ«▒Я«ЙЯ«БЯ»ЇЯ«ЪЯ»ѕЯ«џЯ»Ї Я«џЯ»ЄЯ«░Я»ЇЯ«еЯ»ЇЯ«ц Я«фЯ«┐Я«░Я«ъЯ»ЇЯ«џЯ»Ї Я«ЋЯ«БЯ«┐Я«ц Я««Я»ЄЯ«цЯ»ѕ Я«фЯ«┐Я«│Я«»Я»ЇЯ«џЯ»Ђ Я«фЯ«ЙЯ«ИЯ»ЇЯ«ЋЯ«▓Я«┐Я«ЕЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«фЯ«┐Я«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«хЯ«░Я»Ї, Я«ЄЯ«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«ЋЯ«БЯ«┐Я«ц Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ»Ђ Я«џЯ«░Я«┐Я«»Я«ЙЯ«Е Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«цЯ«ЋЯ«хЯ«┐Я«»Я«▓Я«┐Я«▓Я»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«»Я«хЯ«░Я»Ї.
2. Я««Я«┐Я«ЋЯ»ѕ Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї
(Binomial Theorem for Positive Integral Index)
Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ, Я««Я«┐Я«ЋЯ«хЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«ЋЯ«┤Я»Ї Я«хЯ«ЙЯ«»Я»ЇЯ«еЯ»ЇЯ«ц Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«Е Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї 5.1 Я««Я«┐Я«ЋЯ»ѕ Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї
(Binomial Theorem for Positive Integral Index)
Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«ЄЯ«»Я«▓Я»Ї Я«јЯ«БЯ»Ї n-Я«ЋЯ»ЇЯ«ЋЯ»Ђ,
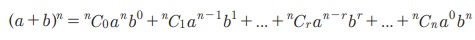 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї Я«ЋЯ«БЯ«┐Я«цЯ«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«▒Я«┐Я«цЯ«▓Я»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«ЄЯ«еЯ»ЇЯ«цЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ»ѕ Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї. Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я««Я«┐Я«ЋЯ»ѕ Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»Ї n-Я«ЋЯ»ЇЯ«ЋЯ»Ђ, P(n) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ 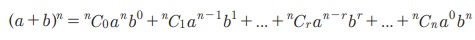
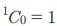 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 1C1 = 1, Я«јЯ«ЕЯ«хЯ»Є, P(1)-Я«ЕЯ»Ї Я«хЯ«▓Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї a1 b0 + a0 b1 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ Я«ЄЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│ (a + b)1 -Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ««Я««Я»Ї. Я«ЄЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї P(1) Я««Я»єЯ«»Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я««Я«┐Я«ЋЯ»ѕ Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»Ї k-Я«ЋЯ»ЇЯ«ЋЯ»Ђ P(k) Я««Я»єЯ«»Я»Ї Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ,
Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 1C1 = 1, Я«јЯ«ЕЯ«хЯ»Є, P(1)-Я«ЕЯ»Ї Я«хЯ«▓Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї a1 b0 + a0 b1 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ Я«ЄЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│ (a + b)1 -Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ««Я««Я»Ї. Я«ЄЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї P(1) Я««Я»єЯ«»Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я««Я«┐Я«ЋЯ»ѕ Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»Ї k-Я«ЋЯ»ЇЯ«ЋЯ»Ђ P(k) Я««Я»єЯ«»Я»Ї Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ,
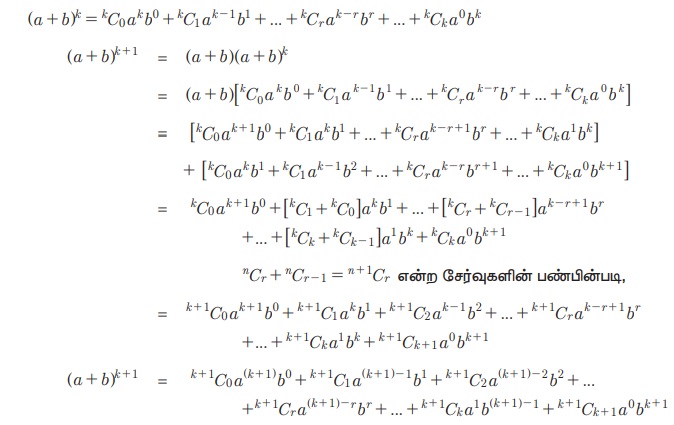
Я«јЯ«ЕЯ«хЯ»Є, P(k) Я««Я»єЯ«»Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї P(k+1) Я««Я»єЯ«»Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЋЯ«БЯ«┐Я«ц Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«▒Я«┐Я«цЯ«▓Я»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«јЯ«▓Я»ЇЯ«▓Я«Й Я«ЄЯ«»Я«▓Я»Ї Я«јЯ«БЯ»Ї n-Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї P(n) Я««Я»єЯ«»Я»Ї Я«јЯ«Е Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я«ЙЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«јЯ«ЕЯ«хЯ»Є, 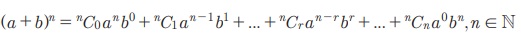
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ:
(i) (a + b)n, n Рѕѕ РёЋ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЕЯ»Ї Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕ,
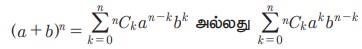 Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
(ii) n Я«ЊЯ«░Я»Ї Я«ЄЯ«»Я«▓Я»Ї Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, (a + b)n Я«јЯ«ЕЯ»ЇЯ«▒ Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«хЯ«┐Я«░Я«┐Я«хЯ«┐Я«▓Я»Ї (n + 1) Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
(iii) 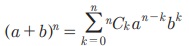 Я«ЄЯ«▓Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»ЂЯ««Я»Ї a-Я«ЕЯ»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»ЂЯ««Я»Ї b-Я«ЕЯ»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЁЯ«цЯ«┐Я«ЋЯ«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«фЯ»ІЯ«цЯ«┐Я«▓Я»ЂЯ««Я»Ї, Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»ЂЯ««Я»Ї, a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b -Я«ЕЯ»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«јЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»ЂЯ««Я»Ї n Я«єЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«ЄЯ«▓Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»ЂЯ««Я»Ї a-Я«ЕЯ»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»ЂЯ««Я»Ї b-Я«ЕЯ»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЁЯ«цЯ«┐Я«ЋЯ«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«фЯ»ІЯ«цЯ«┐Я«▓Я»ЂЯ««Я»Ї, Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»ЂЯ««Я»Ї, a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b -Я«ЕЯ»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«јЯ«фЯ»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»ЂЯ««Я»Ї n Я«єЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
(iv) n Я«њЯ«░Я»Ђ Я«ЄЯ«»Я«▓Я»Ї Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, (a + b)n Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЕЯ»Ї Я«хЯ«┐Я«░Я«┐Я«хЯ«┐Я«▓Я»Ї (r +1) Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ 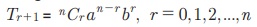 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
(v) (a + b)(a + b)...(a + b), Я«јЯ«ЕЯ»ЇЯ«▒ n Я«ЋЯ«ЙЯ«░Я«БЯ«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»Ї br Я«љЯ«фЯ»Ї Я«фЯ»єЯ«▒, Я«ЄЯ«еЯ»ЇЯ«ц n Я«ЋЯ«ЙЯ«░Я«БЯ«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї r Я«ЋЯ«ЙЯ«░Я«БЯ«┐Я«ЋЯ«│Я»Ї Я«цЯ»ЄЯ«хЯ»ѕ. Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ nCr Я«хЯ«┤Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«еЯ«ЙЯ««Я»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї. Я«ЁЯ«цЯ«ЕЯ«ЙЯ«▓Я»ЇЯ«цЯ«ЙЯ«ЕЯ»Ї, nCr Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ an-rbr -Я«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«хЯ«ЙЯ«Ћ Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
(vi) (a + b)n, n Рѕѕ РёЋ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЕЯ»Ї Я«хЯ«┐Я«░Я«┐Я«хЯ«┐Я«▓Я»Ї Я«цЯ»іЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЂЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«џЯ««Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»Ї Я«џЯ««Я««Я»Ї. Я«ЈЯ«ЕЯ»єЯ«ЕЯ«┐Я«▓Я»Ї, nCr = nCn-r
(vii) (a + b)n, n Рѕѕ РёЋ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЕЯ»Ї Я«хЯ«┐Я«░Я«┐Я«хЯ«┐Я«▓Я»Ї n Я«њЯ«░Я»Ђ Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЋЯ»єЯ«┤Я»ЂЯ«хЯ«┐Я«ЕЯ»Ї Я«ЁЯ«цЯ«┐Я«ЋЯ«фЯ«ЪЯ»ЇЯ«џ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ, ![]() Я«єЯ«ЋЯ»ЂЯ««Я»Ї. n Я«њЯ«░Я»Ђ Я«њЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЋЯ»єЯ«┤Я»ЂЯ«хЯ«┐Я«ЕЯ»Ї Я«ЁЯ«цЯ«┐Я«ЋЯ«фЯ«ЪЯ»ЇЯ«џ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
Я«єЯ«ЋЯ»ЂЯ««Я»Ї. n Я«њЯ«░Я»Ђ Я«њЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЋЯ»єЯ«┤Я»ЂЯ«хЯ«┐Я«ЕЯ»Ї Я«ЁЯ«цЯ«┐Я«ЋЯ«фЯ«ЪЯ»ЇЯ«џ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ  Я«єЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
(viii) (a + b)n, n Рѕѕ РёЋ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЕЯ»Ї Я«хЯ«┐Я«░Я«┐Я«хЯ«┐Я«▓Я»Ї n Я«њЯ«░Я»Ђ Я«ЄЯ«░Я«ЪЯ»ЇЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я««Я»ѕЯ«» Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ 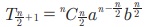 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. n Я«њЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї,
Я«єЯ«ЋЯ»ЂЯ««Я»Ї. n Я«њЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ѕ Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, 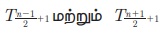 Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«ЄЯ«░Я»Ђ Я««Я»ѕЯ«» Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«ЄЯ«░Я»Ђ Я««Я»ѕЯ«» Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.