Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ, Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я««Я»Ї, Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»Ї, Я«фЯ«»Я«┐Я«▒Я»ЇЯ«џЯ«┐ | Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї - Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї | 11th Mathematics : UNIT 5 : Binomial Theorem, Sequences and Series
11Я«хЯ«цЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 5 : Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї, Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї
Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї
Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї (Finite Series)
Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Ћ, Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«ЙЯ«▓Я«ЙЯ«Е Я«њЯ«░Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї, Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЁЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»Ї (Finite Series) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. (an) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, a1 + a2 +... + an Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. a1 + a2 +... + an Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ ![]() Я«јЯ«Е Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«џЯ«┐Я«▓ Я«еЯ»ЄЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«хЯ«┐Я«ЕЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«цЯ»ЇЯ«цЯ»ЂЯ«хЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«јЯ«│Я«┐Я««Я»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ»іЯ«▒Я»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»Ї a0 + a1 + a2 +... Я«јЯ«Е Я«хЯ«┤Я«ЎЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ a0 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«Е Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«џЯ«┐Я«▓ Я«еЯ»ЄЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«хЯ«┐Я«ЕЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«цЯ»ЇЯ«цЯ»ЂЯ«хЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«јЯ«│Я«┐Я««Я»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ»іЯ«▒Я»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»Ї a0 + a1 + a2 +... Я«јЯ«Е Я«хЯ«┤Я«ЎЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ a0 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
1. Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ, Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«фЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї (Sum of Arithmetic, Geometric and Arithmetico-Geometric Progressions)
Я««Я»ЂЯ«еЯ»ЇЯ«цЯ»ѕЯ«» Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«еЯ«ЙЯ««Я»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї, Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«џЯ«┐Я«▓ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«хЯ«░Я»ѕЯ«»Я«┐Я«▓Я«ЙЯ«Е Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│Я»ІЯ««Я»Ї. Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ»Ђ Я«ЋЯ»ѓЯ«░Я»ЇЯ«хЯ»ІЯ««Я»Ї.
Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї (Sum of Arithmetic and Geometric Progressions)
РЌЈ Я«њЯ«░Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЁЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї (Arithmetic Series) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»ЂЯ«фЯ»ІЯ«▓Я»Ї Я«њЯ«░Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЁЯ«цЯ»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї (Geometric Series) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
РЌЈ Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ (a + (n РђЊ 1)d) -Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї
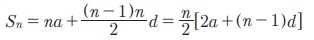
РЌЈ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ (arn-1)-Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї. 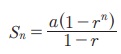
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ, r РЅа 1, Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«еЯ»ЇЯ«ц Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ Я«њЯ«░Я»Ђ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї a,a,a.... Я«єЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї na Я«јЯ«Е Я«јЯ«│Я«┐Я«цЯ«┐Я«▓Я»Ї Я«ЁЯ«▒Я«┐Я«»Я«▓Я«ЙЯ««Я»Ї. Я«ЁЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї, r РЅа 1 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, 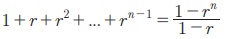
Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ РђЊ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї (Sum of Arithmetico-Geometric Progressions)
РЌЈ Я«њЯ«░Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ - Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЁЯ«цЯ»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ - Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї (Arithmetico-Geometric Series) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
РЌЈ ((a + (n - 1)d)rn-1) Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 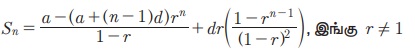
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.16 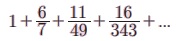 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ - Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ - Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
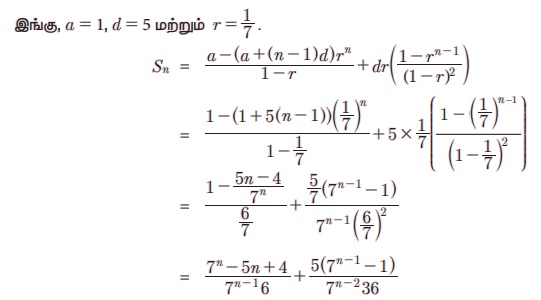
2. Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«▓Я»ѕЯ«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї (Telescopic Summation for Finite Series)
Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«Б Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Ћ Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«▒Я»ѕ Я«цЯ»іЯ«▓Я»ѕ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»ѕ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї. Я«хЯ«┤Я«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«Ћ Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ«ЪЯ»ѕЯ«џЯ«┐ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«цЯ«хЯ«┐Я«░ Я««Я«▒Я»ЇЯ«▒ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»ѕЯ«»Я»іЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«еЯ»ђЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ««Я»Ї. Я«ЄЯ«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«еЯ»ђЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«» Я«фЯ«┐Я«ЕЯ»ЇЯ«фЯ»Ђ, Я«цЯ»іЯ«▓Я»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«ц Я«ЋЯ«ЪЯ»ѕЯ«џЯ«┐ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«хЯ»єЯ«ЋЯ»Ђ Я«ЁЯ«░Я»ЂЯ«ЋЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є Я«ЄЯ«еЯ»ЇЯ«ц Я««Я»ЂЯ«▒Я»ѕ Я«цЯ»іЯ«▓Я»ѕЯ«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї (Telescopic Summation) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«џЯ«┐Я«▓ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»ѕЯ«џЯ»Ї Я«џЯ»єЯ«»Я»ЇЯ«»Я«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.17 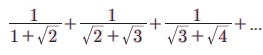 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї k Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ tk Я«јЯ«ЕЯ»ЇЯ«Ћ. 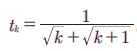 Я«ЄЯ«цЯ»ѕ Я«ЄЯ«░Я»Ђ Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ««Я«ЙЯ«Ћ Я«јЯ«┤Я»ЂЯ«цЯ«┐Я«ЕЯ«ЙЯ«▓Я»Ї Я«цЯ»іЯ«▓Я»ѕЯ«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕ Я««Я»ѓЯ«▓Я««Я»Ї Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«ЄЯ«цЯ»ѕ Я«ЄЯ«░Я»Ђ Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ««Я«ЙЯ«Ћ Я«јЯ«┤Я»ЂЯ«цЯ«┐Я«ЕЯ«ЙЯ«▓Я»Ї Я«цЯ»іЯ«▓Я»ѕЯ«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕ Я««Я»ѓЯ«▓Я««Я»Ї Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЕЯ«хЯ»Є,
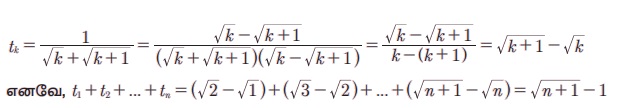
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.18 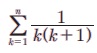 -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
-Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ :
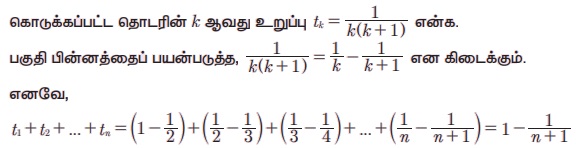
Я«фЯ«»Я«┐Я«▒Я»ЇЯ«џЯ«┐ 5.3
1. Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї 10 Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 52 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї 15 Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 77 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я««Я»ЂЯ«цЯ«▓Я»Ї 20 Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
2. 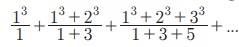 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї 17 Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї 17 Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
3. Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
(i) 8+88+888+8888+...
(ii) 6 + 66 + 666 + 6666 +....
4. 1 + (1 + 4) + (1 + 4 + 42) + (1 + 4 + 42 + 43) +... Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
5. 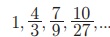 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї n Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї n Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
6. 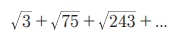 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 435Рѕџ3 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, n -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 435Рѕџ3 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, n -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
7. Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї (m+n) Я«єЯ«хЯ«цЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (m-n) Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї m Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ѕЯ«фЯ»ЇЯ«фЯ»ІЯ«▓Я»Ї Я«ЄЯ«░Я»ЂЯ««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
8. Я«њЯ«░Я»ЂЯ«хЯ«░Я»Ї Рѓ╣3250 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЋЯ»ѕЯ«»Я»ѕ Я««Я»ЂЯ«цЯ«▓Я»Ї Я««Я«ЙЯ«цЯ««Я»Ї Рѓ╣20-Я««Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я««Я«ЙЯ«цЯ««Я»ЂЯ««Я»Ї Рѓ╣15 Я«ЁЯ«цЯ«┐Я«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«»Я»ЂЯ««Я»Ї Я«џЯ»єЯ«▓Я»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«хЯ«░Я»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«ЙЯ«░Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«хЯ«░Я»Ї Я«ЁЯ«еЯ»ЇЯ«цЯ«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ѕЯ«»Я»ѕ Я««Я»ЂЯ«┤Я»ЂЯ««Я»ѕЯ«»Я«ЙЯ«Ћ Я«цЯ«┐Я«░Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«џЯ»Ї Я«џЯ»єЯ«▓Я»ЂЯ«цЯ»ЇЯ«ц Я«јЯ«цЯ»ЇЯ«цЯ«ЕЯ»ѕ Я««Я«ЙЯ«цЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї?
9. Я«њЯ«░Я»Ђ Я«фЯ«еЯ»ЇЯ«цЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї 20 Я«фЯ«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«│Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї 4Я««Я»ђ Я«ЄЯ«ЪЯ»ѕЯ«хЯ»єЯ«│Я«┐Я«»Я«┐Я«▓Я»Ї Я«њЯ«░Я»Є Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я««Я»ЂЯ«цЯ«▓Я»Ї Я«фЯ«еЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЄЯ«ЪЯ»ѕЯ«хЯ»єЯ«│Я«┐ 24Я««Я»ђ. Я«њЯ«░Я»Ђ Я«фЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я«ЙЯ«│Я«░Я»Ї Я«њЯ«░Я»Ђ Я«еЯ»ЄЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«фЯ«еЯ»ЇЯ«цЯ»Ђ Я«хЯ»ђЯ«цЯ««Я»Ї Я«јЯ«▓Я»ЇЯ«▓Я«Й Я«фЯ«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«хЯ«еЯ»ЇЯ«цЯ»Ђ Я«џЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ Я«јЯ«хЯ»ЇЯ«хЯ«│Я«хЯ»Ђ Я«цЯ»ѓЯ«░Я««Я»Ї Я«ЊЯ«Ъ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.
10. Я«еЯ»ЂЯ«БЯ»ЇЯ«БЯ»ЂЯ«»Я«┐Я«░Я»Ї Я«хЯ«│Я«░Я»ЇЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«┐Я«▓Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я««Я«БЯ«┐ Я«еЯ»ЄЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«еЯ»ЂЯ«БЯ»ЇЯ«БЯ»ЂЯ«»Я«┐Я«░Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я«ЙЯ«ЕЯ«цЯ»Ђ Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я»ЂЯ«еЯ»ЇЯ«цЯ»ѕЯ«» Я««Я«БЯ«┐ Я«еЯ»ЄЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ Я«фЯ»ІЯ«▓Я»Ї Я«ЄЯ«░Я»Ђ Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«ЙЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«єЯ«░Я««Я»ЇЯ«фЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї 30 Я«еЯ»ЂЯ«БЯ»ЇЯ«БЯ»ЂЯ«»Я«┐Я«░Я»ЇЯ«ЋЯ«│Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї 2 Я«єЯ«хЯ«цЯ»Ђ, 4 Я«єЯ«хЯ«цЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї n Я«єЯ«хЯ«цЯ»Ђ Я««Я«БЯ«┐Я«еЯ»ЄЯ«░ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я«јЯ«цЯ»ЇЯ«цЯ«ЕЯ»ѕ Я«еЯ»ЂЯ«БЯ»ЇЯ«БЯ»ЂЯ«»Я«┐Я«░Я»ЇЯ«ЋЯ«│Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
11. Я«њЯ«░Я»Ђ Я«хЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«»Я«┐Я«▓Я»Ї Я«џЯ»єЯ«▓Я»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Рѓ╣500 Я«єЯ«ЕЯ«цЯ»Ђ, 10% Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«хЯ«ЪЯ»ЇЯ«ЪЯ«┐ Я«хЯ»ђЯ«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї, 10 Я«єЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«јЯ«хЯ»ЇЯ«хЯ«│Я«хЯ«ЙЯ«Ћ Я««Я«ЙЯ«▒Я»ЂЯ««Я»Ї.
12. Я«њЯ«░Я»Ђ Я«еЯ«ЋЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї, Я«хЯ»ѕЯ«░Я«ИЯ»Ї Я«еЯ»ІЯ«»Я«┐Я«ЕЯ«ЙЯ«▓Я»Ї Я«ЈЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«џЯ»ЂЯ«ЋЯ«ЙЯ«цЯ«ЙЯ«░ Я«ЋЯ»ЄЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ«ЙЯ«▓Я»Ї Я««Я«ЋЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЄЯ«»Я«▓Я»ЇЯ«фЯ»Ђ Я«хЯ«ЙЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ѕ Я«фЯ«ЙЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ«цЯ»Ђ. Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«еЯ«ЙЯ«│Я»ЂЯ««Я»Ї Я«ЁЯ«еЯ»ЇЯ«ц Я«еЯ»ІЯ«»Я»Ї Я«цЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«хЯ»ѕЯ«░Я«ИЯ»Ї Я«ЋЯ«┐Я«░Я»ЂЯ««Я«┐Я«ЋЯ«│Я»Ї Я«њЯ«░Я»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«фЯ«░Я«хЯ«┐ Я«хЯ«░Я»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«▒Я»ЇЯ«▒Я»Ђ Я«ЋЯ«┐Я«░Я»ЂЯ««Я«┐Я«ЋЯ«│Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«еЯ«ЙЯ«│Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я»ЂЯ«еЯ»ЇЯ«цЯ»ѕЯ«» Я«еЯ«ЙЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ»ІЯ«▓Я»Ї Я«ЄЯ«░Я»ЂЯ««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«ЙЯ«Ћ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я««Я»ЂЯ«цЯ«▓Я»Ї Я«еЯ«ЙЯ«│Я«┐Я«▓Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ 5 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«еЯ»ЇЯ«ц Я«ЋЯ«┐Я«░Я»ЂЯ««Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ Я«јЯ«еЯ»ЇЯ«ц Я«еЯ«ЙЯ«│Я«┐Я«▓Я»Ї 1,50,000-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«цЯ«┐Я«ЋЯ««Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
3. Я«џЯ«┐Я«▓ Я«џЯ«┐Я«▒Я«фЯ»ЇЯ«фЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї (Some Special Finite Series)
Я«ЄЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«еЯ«ЙЯ««Я»Ї AP, GP Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«Б Я«џЯ«┐Я«▓ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«» Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
1. Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЄЯ«»Я«▓Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї
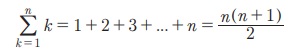
(Я«ЄЯ«цЯ»ѕ AP Я«ЄЯ«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.)
2. Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЄЯ«»Я«▓Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї
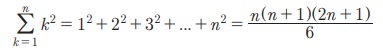
[a3 - b3 = (a - b)(a2 + ab + b2) Я«јЯ«ЕЯ»ЇЯ«▒ Я««Я»ЂЯ«▒Я»ЇЯ«▒Я»іЯ«░Я»ЂЯ««Я»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.]
3. Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЄЯ«»Я«▓Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї
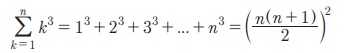
[k4-(k-1)4 = (4k3 РђЊ 6k2 + 4k - 1) Я«јЯ«ЕЯ»ЇЯ«▒ Я««Я»ЂЯ«▒Я»ЇЯ«▒Я»іЯ«░Я»ЂЯ««Я»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐, Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ«БЯ»ЇЯ«Ъ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ѕ Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«Ћ.]
Я«ЄЯ«еЯ»ЇЯ«ц Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«еЯ»ЇЯ«цЯ»ѕЯ«» Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«Е Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«Ћ.