Я«хЯ«░Я»ѕЯ«»Я«▒Я»ѕ, Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я««Я»Ї, Я«цЯ»ђЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»Ї, Я«фЯ«»Я«┐Я«▒Я»ЇЯ«џЯ«┐ | Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї - Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї | 11th Mathematics : UNIT 5 : Binomial Theorem, Sequences and Series
11Я«хЯ«цЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 5 : Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї, Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї
Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї
Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї (Infinite Sequences and Series)
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я«ЙЯ«ЕЯ«цЯ»Ђ Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«еЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«ЁЯ«▒Я«┐Я«» Я«еЯ«ЙЯ««Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«» Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«│ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ. ┬й + ┬╝ + 1/8 +... Я«јЯ«ЕЯ»ЇЯ«▒ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я«ЙЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї. Я«ЄЯ«цЯ«┐Я«▓Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ««Я»Ї Я««Я«┐Я«ЋЯ»ѕ, Я«ЄЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«јЯ«БЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЁЯ«│Я«┐Я«ЋЯ»ЇЯ«Ћ Я«ЄЯ«»Я«▓Я»ЂЯ««Я«Й? Я««Я»ЂЯ«цЯ«▓Я»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«хЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ«цЯ»Ђ Я«ЋЯ«ЪЯ«┐Я«ЕЯ««Я«ЙЯ«Ћ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«»Я«ЙЯ«цЯ«цЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«цЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«џЯ«┐Я«▒Я«┐Я«цЯ»Ђ Я«џЯ«┐Я«▒Я«┐Я«цЯ«ЙЯ«Ћ Я«еЯ«ЋЯ«░Я»ЂЯ«хЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
Я«ЄЯ«цЯ»Ї Я«цЯ«▓Я»ѕЯ«фЯ»ЇЯ«фЯ»ѕ Я«єЯ«░Я»ЇЯ«хЯ««Я»ЂЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЪЯ«ЕЯ»Ї Я«цЯ»іЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«хЯ»ІЯ««Я»Ї. A, B Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЄЯ«░Я»Ђ Я«цЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї. A Я«цЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я««Я»ЂЯ«┤Я»Ђ Я«ЁЯ«фЯ»ЇЯ«фЯ«цЯ»ЇЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї B Я«цЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»ѕ Я«ЋЯ«ЙЯ«▓Я«┐Я«»Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї. A Я«цЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ«фЯ»ЇЯ«фЯ«цЯ»ЇЯ«цЯ»ѕ Я«ЄЯ«░Я»ЂЯ«џЯ««Я«фЯ«ЙЯ«ЋЯ««Я«ЙЯ«Ћ Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐ Я«њЯ«░Я»Ђ Я«фЯ«ЙЯ«ЋЯ«цЯ»ЇЯ«цЯ»ѕ B Я«цЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї. Я««Я«▒Я»ЂЯ«фЯ«ЪЯ«┐Я«»Я»ЂЯ««Я»Ї A Я«ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«фЯ«ЙЯ«цЯ«┐ Я«ЁЯ«фЯ»ЇЯ«фЯ«цЯ»ЇЯ«цЯ»ѕ Я«фЯ«ЙЯ«цЯ«┐Я«»Я«ЙЯ«Ћ Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ«┐ Я«њЯ«░Я»Ђ Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я»ѕ B Я«ЄЯ«▓Я»Ї Я«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«цЯ»Ђ Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї Я«ЄЯ«▒Я»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї A Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї B Я«цЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«јЯ«хЯ»ЇЯ«хЯ«│Я«хЯ»Ђ Я«ЁЯ«фЯ»ЇЯ«фЯ««Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»ѕ Я«еЯ«ЙЯ««Я»Ї Я«ЋЯ»ђЯ«┤Я»Є Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«Ћ Я«цЯ«░Я»ЂЯ«хЯ»ІЯ««Я»Ї.
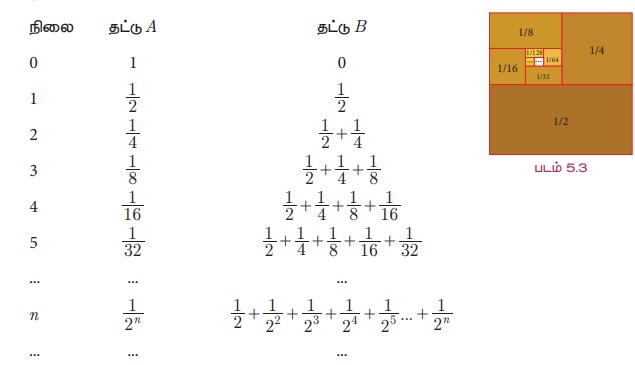
Я«ЄЯ«цЯ«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ "Я««Я»ЂЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї" (finally) Я«цЯ«ЪЯ»ЇЯ«ЪЯ»Ђ A Я«ЄЯ«▓Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«цЯ»Ђ, B Я«ЄЯ«▓Я»Ї Я«њЯ«░Я»Ђ Я««Я»ЂЯ«┤Я»Ђ Я«ЁЯ«фЯ»ЇЯ«фЯ««Я»ЂЯ««Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ«цЯ»Ї Я«цЯ»ІЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ A Я«цЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ»Ђ 0, B Я«цЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ»Ђ 1 Я«јЯ«ЕЯ«цЯ»Ї Я«цЯ»ІЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї.
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ  Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я«цЯ»ЇЯ«цЯ»ѕ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ "Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ" (goes) Я«јЯ«Е Я«ЅЯ«БЯ«░Я«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я«цЯ»ЇЯ«цЯ»ѕ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ "Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ" (goes) Я«јЯ«Е Я«ЅЯ«БЯ«░Я«▓Я«ЙЯ««Я»Ї.
Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї  Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ 1 Я«љ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ "Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ" Я«јЯ«Е Я«ЅЯ«БЯ«░Я«▓Я«ЙЯ««Я»Ї
Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ 1 Я«љ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ "Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ" Я«јЯ«Е Я«ЅЯ«БЯ«░Я«▓Я«ЙЯ««Я»Ї
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, 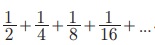 -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ 1.
-Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ 1.
Я«ЄЯ«фЯ»ЇЯ«фЯ«┐Я«░Я«┐Я«хЯ«┐Я«▓Я»Ї РђўЯ««Я»ЂЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»ЇРђЎ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 'Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ' Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ»іЯ«▒Я»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«еЯ»ЇЯ«ц Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«Е Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї, Я«ЄЯ«цЯ»ЂЯ«фЯ»ІЯ«▓Я»Ї Я««Я»ЂЯ«ЪЯ«┐Я«хЯ«▒Я»ЇЯ«▒ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ«цЯ»Ђ Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«»Я»ЂЯ««Я»Ї Я«ЁЯ«▒Я«┐Я«хЯ»ІЯ««Я»Ї.
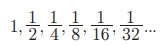 Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я«цЯ»ЇЯ«цЯ»ѕ РђюЯ«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ" Я«јЯ«Е Я«ЅЯ«БЯ«░Я«▓Я«ЙЯ««Я»Ї.
Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я«цЯ»ЇЯ«цЯ»ѕ РђюЯ«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ" Я«јЯ«Е Я«ЅЯ«БЯ«░Я«▓Я«ЙЯ««Я»Ї.
Я«ЄЯ«цЯ»Є Я«фЯ»ІЯ«▓Я»Ї 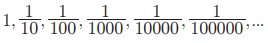 Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я«цЯ»ЇЯ«цЯ»ѕ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«јЯ«Е Я«ЅЯ«БЯ«░Я«▓Я«ЙЯ««Я»Ї.
Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я«цЯ»ЇЯ«цЯ»ѕ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«јЯ«Е Я«ЅЯ«БЯ«░Я«▓Я«ЙЯ««Я»Ї.
(an) Я«њЯ«░Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї a Я«њЯ«░Я»Ђ Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ»ЇЯ«Ћ.
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«јЯ«еЯ»ЇЯ«ц Я«њЯ«░Я»Ђ Я««Я«┐Я«ЋЯ«џЯ»Ї Я«џЯ«┐Я«▒Я«┐Я«» Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«БЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї, Я«ЈЯ«цЯ»І Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«▓Я»Ї an - Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї a-Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»ѓЯ«░Я««Я»Ї Я«ЁЯ«еЯ»ЇЯ«ц Я«јЯ«БЯ»ЇЯ«БЯ»ѕЯ«хЯ«┐Я«Ъ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«хЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї, n Я«єЯ«ЕЯ«цЯ»Ђ Рѕъ-Я«љ Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ, an Я«єЯ«ЕЯ«цЯ»Ђ a-Я«љ Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«јЯ«ЕЯ«▓Я«ЙЯ««Я»Ї. Я«еЯ»ЂЯ«ЪЯ»ЇЯ«фЯ««Я«ЙЯ«Ћ Я«ЋЯ»ѓЯ«▒ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я«ЙЯ«»Я«┐Я«ЕЯ»Ї nРєњРѕъ Я«јЯ«ЕЯ«┐Я«▓Я»Ї an Рєњ a Я«јЯ«ЕЯ«▓Я«ЙЯ««Я»Ї.
Я«хЯ»ЄЯ«▒Я»ЂЯ«хЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЋЯ»ѓЯ«▒Я»ЂЯ«хЯ«цЯ«ЙЯ«»Я«┐Я«ЕЯ»Ї an - Я«єЯ«ЕЯ«цЯ»Ђ Я«јЯ«▓Я»ЇЯ«▓Я»ѕ Я«хЯ«┤Я«┐Я«»Я«ЙЯ«Ћ a-Я«љ Я«ЁЯ«ЪЯ»ѕЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«јЯ«ЕЯ«▓Я«ЙЯ««Я»Ї. Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ nРєњРѕъ Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ an -Я«ЕЯ»Ї Я«јЯ«▓Я»ЇЯ«▓Я»ѕ a Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»ѕ, Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ (an) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ a Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ»ѓЯ«▒Я«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»ѕЯ«»Я»Є Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї 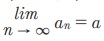 Я«јЯ«Е Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї,
Я«јЯ«Е Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї,
Я«ЁЯ«цЯ»Є Я«џЯ««Я«»Я««Я»Ї 1, 0, 1, 0, 1, 0, 1 ... Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«ЈЯ«цЯ»І Я«њЯ«░Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«▒ Я«ЄЯ«»Я«▓Я«ЙЯ«цЯ»Ђ. Я«ЄЯ«цЯ»Ђ Я«јЯ«еЯ»ЇЯ«ц Я«њЯ«░Я»Ђ Я«јЯ«▓Я»ЇЯ«▓Я»ѕ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«ЙЯ«Ћ Я«џЯ»єЯ«▓Я»ЇЯ«▓Я«хЯ«┐Я«▓Я»ЇЯ«▓Я»ѕ. Я«јЯ«ЕЯ«хЯ»Є, Я«ЄЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«јЯ«▓Я»ЇЯ«▓Я»ѕ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ««Я»Ї Я«ЄЯ«▓Я»ЇЯ«▓Я»ѕ. Я«ЁЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐ Я«њЯ«░Я»Ђ Я«јЯ«▓Я»ЇЯ«▓Я»ѕЯ«»Я»ѕ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«еЯ«ЋЯ«░Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«њЯ«░Я»ЂЯ««Я»ѕЯ«цЯ»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕ Я«ЅЯ«ЪЯ»ѕЯ«»Я«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
1. Я«фЯ«┐Я«фЯ»ЂЯ«ЕЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ (Fibonacci Sequence)
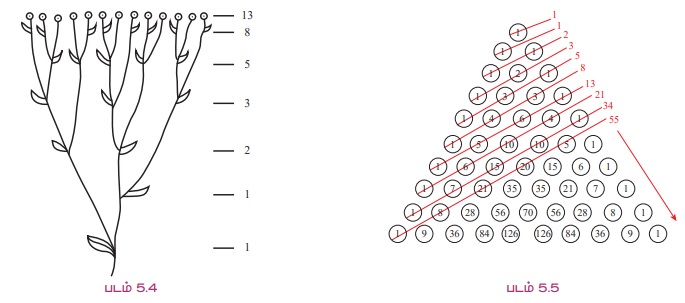
Я«фЯ«┐Я«фЯ»ЂЯ«ЕЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї 1, 1 Я«єЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЕЯ»ЇЯ«ЕЯ«░Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЄЯ«░Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«┐ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒ Я«њЯ«░Я»Ђ Я«јЯ«БЯ»ЇЯ«Ћ Я«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ, 1, 1, 2, 3, 5, 8, 13, 21, 34,.... Я«јЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«ЄЯ«цЯ«ЕЯ»Ї Я«хЯ«┐Я«цЯ«┐ xn = xnРѕњ1 + xnРѕњ2, n РЅЦ 3 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї x1 = 1, x2 = 1 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«фЯ«┐Я«фЯ»ЂЯ«ЕЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ«БЯ«┐Я«цЯ««Я»ЄЯ«цЯ»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«фЯ»єЯ«»Я«░Я«ЙЯ«▓Я»Ї Я«ЄЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї Я«фЯ«┐Я«фЯ»ЂЯ«ЕЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ (Fibonacci. Sequence) Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«цЯ»Ђ Я«▓Я«┐Я«»Я«ЕЯ«░Я»ЇЯ«ЪЯ»І Я«фЯ«┐Я«џЯ«Й Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«▓Я«┐Я«»Я«ЕЯ«░Я»ЇЯ«ЪЯ»І Я«фЯ«┐Я«џЯ«ЙЯ«ЕЯ»І Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«фЯ«┐Я«фЯ»ЂЯ«ЕЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«цЯ»іЯ«ЪЯ«░Я»Ї 1202 Я«ЄЯ«▓Я»Ї Я««Я»ЂЯ«цЯ«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я«┐Я«▓Я»Ї Я«▓Я«┐Я«фЯ«░Я»Ї Я«ЁЯ«фЯ«ЙЯ«џЯ«┐ Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЁЯ«▒Я«┐Я««Я»ЂЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ. Я«фЯ«┐Я«џЯ«ЕЯ»Ї Я«еЯ«ЋЯ«░ Я«хЯ«БЯ«┐Я«ЋЯ«░Я«┐Я«ЕЯ»Ї Я««Я«ЋЯ«ЕЯ«ЙЯ«Е Я«фЯ«┐Я«фЯ»ЂЯ«ЕЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐, Я«фЯ«▓ Я«ЄЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«фЯ«»Я«БЯ««Я»Ї Я«џЯ»єЯ«»Я»ЇЯ«цЯ»Ђ Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«Ћ Я«хЯ«БЯ«┐Я«ЋЯ««Я»Ї Я«џЯ»єЯ«»Я»ЇЯ«цЯ«хЯ«░Я»Ї. Я«хЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«Ћ Я«цЯ»іЯ«┤Я«┐Я«▓Я«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ«БЯ«┐Я«цЯ««Я»Ї Я««Я«┐Я«Ћ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я««Я«ЙЯ«ЕЯ«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї Я«фЯ«┐Я«фЯ»ЂЯ«ЕЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«цЯ«ЕЯ«цЯ»Ђ Я«џЯ«┐Я«▒Я»Ђ Я«хЯ«»Я«цЯ»Ђ Я««Я»ЂЯ«цЯ«▒Я»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Є Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ«ЙЯ«Е Я«фЯ»ЄЯ«░Я«ЙЯ«░Я»ЇЯ«хЯ«цЯ»ЇЯ«цЯ»ѕ Я«хЯ«│Я«░Я»ЇЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«ЙЯ«░Я»Ї.
Я«ЄЯ«еЯ»ЇЯ«цЯ»Ђ РђЊ Я«ЁЯ«░Я«ЙЯ«фЯ«┐Я«ЋЯ»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«БЯ«┐Я«ц Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«цЯ«ЙЯ«ЕЯ»Ї Я««Я»ЂЯ«цЯ«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я«┐Я«▓Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«» Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«░Я»Ї. Я«фЯ«┐Я«фЯ»ЂЯ«ЕЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«хЯ«Ъ Я«єЯ«фЯ»ЇЯ«фЯ«┐Я«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ«ЙЯ«хЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«ц Я«фЯ»ІЯ«цЯ»Ђ Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«ЋЯ«▒Я»ЇЯ«▒Я«▒Я«┐Я«еЯ»ЇЯ«цЯ«ЙЯ«░Я»Ї. Я«▓Я«┐Я«фЯ«░Я»Ї Я«ЁЯ«фЯ«ЙЯ«џЯ«┐ Я«фЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЋЯ««Я»Ї Я«хЯ»єЯ«│Я«┐Я«хЯ«░Я»ЂЯ«хЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЕЯ»ЇЯ«фЯ»Ђ Я«▓Я«цЯ»ЇЯ«цЯ»ђЯ«ЕЯ»Ї Я«фЯ»ЄЯ«џЯ»ЂЯ««Я»Ї Я«ЅЯ«▓Я«ЋЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«цЯ«џЯ«« Я«јЯ«БЯ»Ї Я««Я»ЂЯ«▒Я»ѕ Я«ЁЯ«▒Я«┐Я««Я»ЂЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ«ЙЯ««Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«цЯ»Ђ. Я«ЄЯ«хЯ«░Я»Ї Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї, Я«хЯ«БЯ«┐Я«Ћ Я«јЯ«БЯ»ЇЯ«ЋЯ«БЯ«┐Я«цЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«фЯ«▓ Я«фЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│Я«ЙЯ«░Я»Ї. Я«ЄЯ«хЯ«░Я»Ї Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я««Я»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«» Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«хЯ«цЯ«┐Я«▓Я»ЂЯ««Я»Ї Я«фЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«цЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│Я«ЙЯ«░Я»Ї.

Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, 6 Я«єЯ«хЯ«цЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 7 Я«єЯ«хЯ«цЯ»Ђ Я«ЄЯ«ЪЯ«цЯ»ЇЯ«цЯ»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«Ъ 8 Я«єЯ«хЯ«цЯ»Ђ Я«ЄЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ x8 = 8 + 13 = 21
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ: Я«фЯ«┐Я«фЯ»ЂЯ«ЕЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«єЯ«░Я»ЇЯ«хЯ««Я»ЂЯ«│Я»ЇЯ«│ Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ«хЯ«ЕЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«ЋЯ«хЯ«ЕЯ«┐Я«»Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї
(i) Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«хЯ«цЯ»Ђ Я«јЯ«БЯ»ЇЯ«БЯ»ЂЯ««Я»Ї 3 Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. (t3 = 2)
(ii) Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ«ЙЯ«хЯ«цЯ»Ђ Я«јЯ«БЯ»ЇЯ«БЯ»ЂЯ««Я»Ї 4 Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. (t4 = 3)
(iii) Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«љЯ«еЯ»ЇЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«јЯ«БЯ»ЇЯ«БЯ»ЂЯ««Я»Ї 5 Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. (t5 = 5)
(iv) Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ n Я«єЯ«хЯ«цЯ»Ђ Я«јЯ«БЯ»ЇЯ«БЯ»ЂЯ««Я»Ї n Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я««Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«цЯ»іЯ«ЪЯ«░Я»Ї (Infinite Series)
(an) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ«▒Я»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, a1 + a2 +.... Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ«▒Я»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»ѕ, ![]() Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«ЄЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї 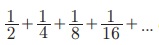 Я«јЯ«ЕЯ»ЇЯ«▒ Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«цЯ»іЯ«ЪЯ«░Я»ѕЯ«фЯ»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ»ІЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 1 Я«јЯ«Е Я«ЅЯ«БЯ«░Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ Я«ЁЯ«фЯ»ЇЯ«фЯ««Я»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї B Я«цЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ«фЯ»ЇЯ«фЯ««Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«▓Я»ЂЯ««Я»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«цЯ»Ђ.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«цЯ»іЯ«ЪЯ«░Я»ѕЯ«фЯ»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ»ІЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 1 Я«јЯ«Е Я«ЅЯ«БЯ«░Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ Я«ЁЯ«фЯ»ЇЯ«фЯ««Я»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї B Я«цЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ«фЯ»ЇЯ«фЯ««Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«▓Я»ЂЯ««Я»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«цЯ»Ђ.
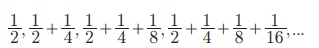
Я«ЄЯ«цЯ«ЕЯ»Ї n Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ, 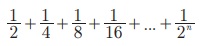 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ 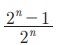 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«еЯ»ЇЯ«ц Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Sn Я«јЯ«ЕЯ«┐Я«▓Я»Ї,  Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«цЯ«▓Я«ЙЯ«▓Я»Ї, 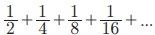 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ 1 Я«јЯ«Е Я«ЅЯ«БЯ«░Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ.
Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ 1 Я«јЯ«Е Я«ЅЯ«БЯ«░Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ.
Я«ЄЯ«цЯ»ЂЯ«фЯ»ІЯ«▓Я»Ї (an) Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»єЯ«»Я»Ї Я«јЯ«БЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї, Sn = a1 + a2 + a3 +....+ an Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«јЯ«▓Я»ЇЯ«▓Я»ѕ S-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ (an) Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї S Я«јЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«│Я«▓Я«ЙЯ««Я»Ї.
Я«ЄЯ«цЯ»ѕ, a1 + a2 + a3 +... = s Я«јЯ«Е Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, Я«ЄЯ«еЯ»ЇЯ«еЯ«┐Я«▓Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЄЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»Ї s -Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ Я«јЯ«Е Я«ЋЯ»ѓЯ«▒Я»ЂЯ«хЯ«цЯ»Ђ Я«хЯ«┤Я«ЋЯ»ЇЯ«ЋЯ««Я»Ї.

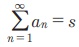 Я«јЯ«Е Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї. Я«џЯ«┐Я«▓ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
Я«јЯ«Е Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї. Я«џЯ«┐Я«▓ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї. 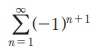 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«цЯ»іЯ«ЪЯ«░Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«цЯ»Ђ. Я«ЈЯ«ЕЯ»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї 1, 0, 1, 0, 1,. Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЕЯ»Ї Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«ЋЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«▓Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я«▒Я»ЇЯ«▒Я«цЯ»Ђ.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«цЯ»іЯ«ЪЯ«░Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«цЯ»Ђ. Я«ЈЯ«ЕЯ»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї 1, 0, 1, 0, 1,. Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЕЯ»Ї Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«ЋЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«▓Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я«▒Я»ЇЯ«▒Я«цЯ»Ђ.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ:
Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«ц Я«хЯ«┐Я«цЯ«┐Я«ЋЯ«│Я»ѕ Я«еЯ«ЙЯ««Я»Ї Я«ЁЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐Я«»Я»Є Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я««Я»ЂЯ«ЪЯ«┐Я«»Я«ЙЯ«цЯ»Ђ.
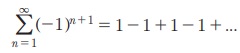 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї.
S = 1 - 1 + 1 = 1 + ..... Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«њЯ«░Я»ЂЯ«хЯ«░Я»Ї S-Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є 0 Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ 1 Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ 1/2 Я«јЯ«Е Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«цЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«џЯ»єЯ«»Я»ЇЯ«»Я«▓Я«ЙЯ««Я»Ї.
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, S = (1 - 1) + (1 - 1) + ...., S = 1 + (-1+1) + (-1 + 1) + .... Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ
1 РђЊ S = 1 - (+ 1 РђЊ 1 + 1 РђЊ 1 + ... = S)
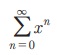 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї x = 1/2 -Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї, x = 2 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЄЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«хЯ«┐Я«▓Я»ЇЯ«▓Я»ѕ. Я«ЄЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ,
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї x = 1/2 -Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї, x = 2 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЄЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«хЯ«┐Я«▓Я»ЇЯ«▓Я»ѕ. Я«ЄЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ, 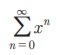 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї x -Я«ЕЯ»Ї Я«џЯ«┐Я«▓ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї x -Я«ЕЯ»Ї Я«џЯ«┐Я«▓ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«хЯ«┐Я«▓Я»ЇЯ«▓Я»ѕ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ЂЯ««Я»Ї Я«цЯ»єЯ«░Я«┐Я«ЋЯ«┐Я«▒Я«цЯ»Ђ. x -Я«ЕЯ»Ї Я«јЯ«еЯ»ЇЯ«ц Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«цЯ»Ђ Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЄЯ«еЯ»ЇЯ«цЯ«фЯ»Ї Я«фЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЁЯ«фЯ»ЇЯ«фЯ«ЙЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ. Я«јЯ«ЕЯ«┐Я«ЕЯ»ЂЯ««Я»Ї, Я«ЄЯ«еЯ»ЇЯ«ц Я«ЁЯ«▓Я«ЋЯ«┐Я«ЕЯ»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«џЯ«┐Я«▓ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї x -Я«ЕЯ»Ї Я«јЯ«еЯ»ЇЯ«ц Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЁЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐ Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ««Я»Ї Я«цЯ«░Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«Е.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї x -Я«ЕЯ»Ї Я«џЯ«┐Я«▓ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї x -Я«ЕЯ»Ї Я«џЯ«┐Я«▓ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«хЯ«┐Я«▓Я»ЇЯ«▓Я»ѕ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ЂЯ««Я»Ї Я«цЯ»єЯ«░Я«┐Я«ЋЯ«┐Я«▒Я«цЯ»Ђ. x -Я«ЕЯ»Ї Я«јЯ«еЯ»ЇЯ«ц Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«цЯ»Ђ Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЄЯ«еЯ»ЇЯ«цЯ«фЯ»Ї Я«фЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЁЯ«фЯ»ЇЯ«фЯ«ЙЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ. Я«јЯ«ЕЯ«┐Я«ЕЯ»ЂЯ««Я»Ї, Я«ЄЯ«еЯ»ЇЯ«ц Я«ЁЯ«▓Я«ЋЯ«┐Я«ЕЯ»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«џЯ«┐Я«▓ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї x -Я«ЕЯ»Ї Я«јЯ«еЯ»ЇЯ«ц Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЁЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐ Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«ЕЯ«ЙЯ«▓Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ««Я»Ї Я«цЯ«░Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«Е.
2. Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї (Infinite Geometric Series)
![]() Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. 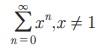 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї. Sn = x0 + x1 + ... + xn Я«јЯ«ЕЯ«┐Я«▓Я»Ї,
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї. Sn = x0 + x1 + ... + xn Я«јЯ«ЕЯ«┐Я«▓Я»Ї, 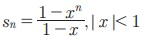
Я«јЯ«Е Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ, xn Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я«цЯ»ЇЯ«цЯ»ѕ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«хЯ«цЯ«ЙЯ«▓Я»Ї Sn Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ 1/1- x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«јЯ«ЕЯ«▓Я«ЙЯ««Я»Ї.
Рђб | x | < 1 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я«еЯ«┐Я«▒Я»ѕЯ«хЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«»Я»ЂЯ««Я»Ї Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї x-Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї 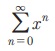 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»ѕ 1/1- x Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, | x | < 1 Я«јЯ«ЕЯ«хЯ»ЂЯ«│Я»ЇЯ«│ Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї x -Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї 1/1- x = 1 + x + x2 + x3 +... Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»ѕ 1/1- x Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, | x | < 1 Я«јЯ«ЕЯ«хЯ»ЂЯ«│Я»ЇЯ«│ Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї x -Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї 1/1- x = 1 + x + x2 + x3 +... Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Рђб | x | < 1 Я«јЯ«ЕЯ«хЯ»ЂЯ«│Я»ЇЯ«│ Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї x -Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї 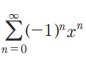 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«цЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»ѕ 1/1- x Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«цЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»ѕ 1/1- x Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, | x | < 1 Я«јЯ«ЕЯ«хЯ»ЂЯ«│Я»ЇЯ«│ Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї x-Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї 1/1- x = 1 + x + x2 + x3 +... Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Рђб | x | < 1/2 Я«јЯ«ЕЯ«хЯ»ЂЯ«│Я»ЇЯ«│ Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї x -Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї 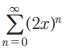 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»ѕ 1 / 1 - 2 x Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ | x | < 1/2 Я«јЯ«ЕЯ«хЯ»ЂЯ«│Я»ЇЯ«│ Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї x РђЊЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»ѕ 1 / 1 - 2 x Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ | x | < 1/2 Я«јЯ«ЕЯ«хЯ»ЂЯ«│Я»ЇЯ«│ Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї x РђЊЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї 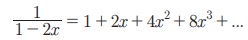 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Рђб Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї x -Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї 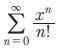 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»ѕ ex Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»ѕ ex Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї x-Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї 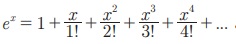 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Рђб x = 0-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї 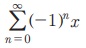 Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ»Ђ.
Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ»Ђ.
Я«џЯ«┐Я«▓ Я«џЯ«┐Я«▒Я«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я«ЁЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«џЯ«┐Я«▓ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
3. Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ РђЊ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї. (Infinite Arithmetico- Geometric Series)
Рђб 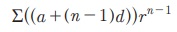 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ - Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї
Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ - Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї
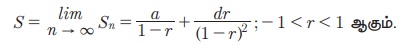
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.19 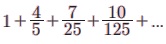 -Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
-Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ, a = 1, d = 3 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї r = 1/5.
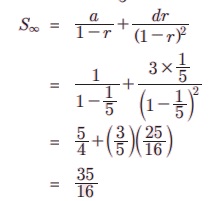
4. Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«цЯ»іЯ«ЪЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«цЯ»іЯ«▓Я»ѕЯ«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї
(Telescopic Summation for Infinite Series)
Я«ЄЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«ЕЯ»ЇЯ«ЕЯ«░Я»Ї 5.5.2 Я«ЄЯ«▓Я»Ї, Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»ѕ Я«цЯ»іЯ«▓Я»ѕЯ«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│Я»ІЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, Я«ЄЯ«цЯ»Є Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»ЂЯ««Я»Ї Я«ЋЯ«ЙЯ«Б Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.20 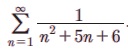 -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
-Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї n Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ an Я«јЯ«ЕЯ»ЇЯ«Ћ. Я«ЁЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї, 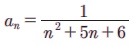 Я«фЯ«ЋЯ»ЂЯ«цЯ«┐ Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«цЯ»ЇЯ«цЯ»ѕ Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐
Я«фЯ«ЋЯ»ЂЯ«цЯ«┐ Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«цЯ»ЇЯ«цЯ»ѕ Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ 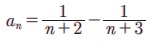 Я«јЯ«Е Я«ЁЯ«▒Я«┐Я«»Я«▓Я«ЙЯ««Я»Ї.
Я«јЯ«Е Я«ЁЯ«▒Я«┐Я«»Я«▓Я«ЙЯ««Я»Ї.
Я«ЄЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Sn Я«јЯ«ЕЯ»ЇЯ«Ћ.
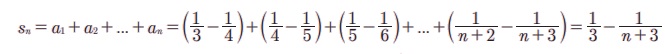
n Я«єЯ«ЕЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я«┐Я«»Я»ѕ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ 1 / n + 3 Я«єЯ«ЕЯ«цЯ»Ђ Я«фЯ»ѓЯ«юЯ»ЇЯ«юЯ«┐Я«»Я«цЯ»ЇЯ«цЯ»ѕ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«▓Я»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, 
5. Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї (Binomial Series)
Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«┐Я«▓Я»Ї Я«еЯ«ЙЯ««Я»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«цЯ»ЇЯ«ц Я«џЯ«┐Я«▓ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї x-Я«ЕЯ»Ї Я«фЯ»іЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ««Я«ЙЯ«Е Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ
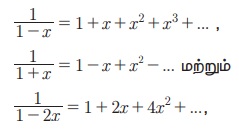
Я«ЁЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї 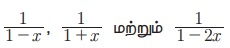 Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я«хЯ»ѕЯ«ЋЯ«│Я»ѕ (1 РђЊ x)-1 (1 + x)-1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (1 РђЊ 2x)-1 Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»Ї (1 + x), (1 РђЊ x)... Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я«хЯ«▒Я»ЇЯ«▒Я«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЋЯ»ЂЯ«▒Я»ѕ Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«Ћ Я«хЯ«ЙЯ«»Я»ЇЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ Я«јЯ«ЕЯ«цЯ»Ї Я«цЯ»єЯ«░Я«┐Я«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕ, Я««Я«┐Я«ЋЯ»ѕ Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ«хЯ»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«ЋЯ«хЯ»І Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї, Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї (1 + x) -Я«ЕЯ»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«Ћ Я«ЋЯ»ѓЯ«Ъ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї, Я«ЈЯ«▒Я»ЇЯ«ЋЯ«ЕЯ«хЯ»Є Я«еЯ«ЙЯ««Я»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї 5.1 Я««Я»ѓЯ«▓Я««Я»Ї, Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ, Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕ Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«цЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│Я»ІЯ««Я»Ї. Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ»ѕ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я«хЯ»ѕЯ«ЋЯ«│Я»ѕ (1 РђЊ x)-1 (1 + x)-1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (1 РђЊ 2x)-1 Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»Ї (1 + x), (1 РђЊ x)... Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я«хЯ«▒Я»ЇЯ«▒Я«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЋЯ»ЂЯ«▒Я»ѕ Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«Ћ Я«хЯ«ЙЯ«»Я»ЇЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ Я«јЯ«ЕЯ«цЯ»Ї Я«цЯ»єЯ«░Я«┐Я«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕ, Я««Я«┐Я«ЋЯ»ѕ Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ«хЯ»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«ЋЯ«хЯ»І Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї, Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї (1 + x) -Я«ЕЯ»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«Ћ Я«ЋЯ»ѓЯ«Ъ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї, Я«ЈЯ«▒Я»ЇЯ«ЋЯ«ЕЯ«хЯ»Є Я«еЯ«ЙЯ««Я»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї 5.1 Я««Я»ѓЯ«▓Я««Я»Ї, Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ, Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕ Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«цЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│Я»ІЯ««Я»Ї. Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ»ѕ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї (Binomial Theorem for Rational Exponent)
Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї 5.4
Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї n-Я«ЋЯ»ЇЯ«ЋЯ»Ђ, | x | < 1 Я«љ Я«еЯ«┐Я«▒Я»ѕЯ«хЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«»Я»ЂЯ««Я»Ї Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї x-Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї 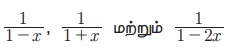 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я«ЙЯ«ЕЯ«цЯ»Ђ Я«ЅЯ«»Я«░Я»Ї Я«ЋЯ«БЯ«┐Я«ц Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ»ѕ Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї Я«ЄЯ«▓Я»ЇЯ«▓Я«ЙЯ««Я«▓Я»Ї Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«џЯ«┐Я«▓ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«еЯ«┐Я«▓Я»ѕЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«џЯ«┐Я«▓ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї
Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я«ЙЯ«ЕЯ«цЯ»Ђ Я«ЅЯ«»Я«░Я»Ї Я«ЋЯ«БЯ«┐Я«ц Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ»ѕ Я«еЯ«┐Я«░Я»ѓЯ«фЯ«БЯ««Я»Ї Я«ЄЯ«▓Я»ЇЯ«▓Я«ЙЯ««Я«▓Я»Ї Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«џЯ«┐Я«▓ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«еЯ«┐Я«▓Я»ѕЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«џЯ«┐Я«▓ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї
1. x Я«љ - x Я«єЯ«Ћ Я«фЯ«┐Я«░Я«цЯ«┐Я«»Я«┐Я«Ъ,
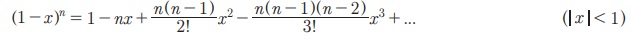
2. n-Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ«цЯ«┐Я«▓Я«ЙЯ«Ћ - n Я«љЯ«фЯ»Ї Я«фЯ«┐Я«░Я«цЯ«┐Я«»Я«┐Я«Ъ,
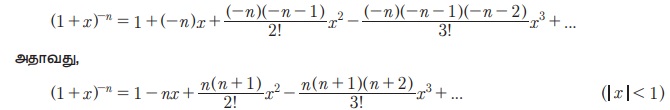
3. x -Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї n -Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ«цЯ«┐Я«▓Я«ЙЯ«Ћ Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є - x Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї - n Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ«┐Я«░Я«цЯ«┐Я«»Я«┐Я«Ъ,
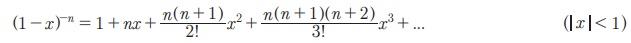
Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї, n Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї Я«јЯ«Е Я«хЯ»єЯ«│Я«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«»Я«ЙЯ«Ћ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»ЂЯ««Я»Ї, Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Е Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«хЯ«ЪЯ«┐Я«хЯ««Я»Ї p/q (qРЅа0) Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, n = p/q Я«јЯ«Е Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕ Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї.
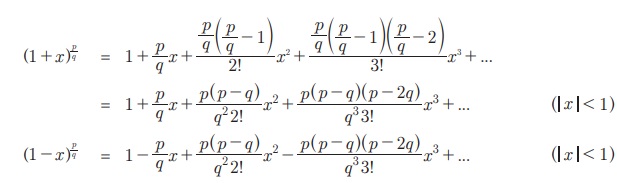
(1+x)n Я«љ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«Ъ Я«ЈЯ«цЯ»ЂЯ«хЯ«ЙЯ«Е Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я»ЄЯ«▓Я»Є Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»ЂЯ««Я»Ї, Я«џЯ«┐Я«▓ Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«»Я«▓Я»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«јЯ«│Я«┐Я««Я»ѕЯ«»Я«ЙЯ«Ћ Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«ЋЯ«ЙЯ«Б Я«еЯ»ЄЯ«░Я«ЪЯ«┐Я«»Я«ЙЯ«Е Я«џЯ«┐Я«▓ Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«цЯ»ЄЯ«хЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я«ЙЯ«Е Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«хЯ«┐Я«░Я«┐Я«хЯ«┐Я«▓Я»ЂЯ««Я»Ї Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЅЯ«▒Я»ЇЯ«▒Я»Ђ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ«▓Я»Ї, Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я««Я«┐Я«ЋЯ«хЯ»ЂЯ««Я»Ї Я«јЯ«│Я«┐Я«цЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«џЯ«┐Я«▓Я«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«еЯ«ЙЯ««Я»Ї Я«фЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я«▓Я«┐Я«ЪЯ»ЂЯ«хЯ»ІЯ««Я»Ї.
1. (1+x)-1 = 1 РђЊ x + x2 = x3 +....
2. (1-x)-1 = 1 + x + x2 + x3 +...
3. (1-x)-2 = 1 + 2x + 3x2 + 4x3 + 5x4+ + 6x5 +...
4. (1 + x)-2 = 1- 2x + 3x2 - 4x3 + 5x4 РђЊ 6x5 + ...
Я«ЄЯ«хЯ»ѕ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї | x | < 1 Я«јЯ«ЕЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Є Я«фЯ»іЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.21 | x | < 1 Я«јЯ«ЕЯ»ЇЯ«▒ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ, (1 + x)2/3 Я«љ Я««Я»ЂЯ«цЯ«▓Я»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«хЯ«░Я»ѕ Я«хЯ«┐Я«░Я«┐Я«хЯ»ЂЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
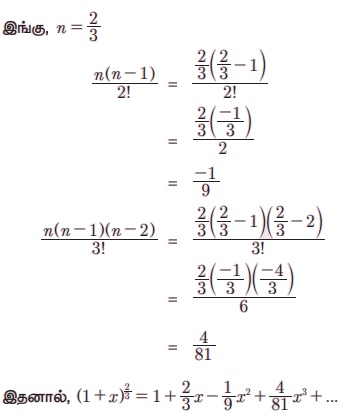
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.22 1/(1+3x)2 Я«љ x-Я«ЕЯ»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я«ЙЯ«Ћ Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«џЯ»єЯ«»Я»ЇЯ«Ћ. Я«ЁЯ«еЯ»ЇЯ«ц Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«џЯ«░Я«┐Я«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«Е x -Я«ЕЯ»Ї Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
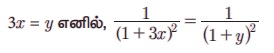
Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ, 1/(1+y)2 Я«љ Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»Ї y-Я«ЕЯ»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я«ЙЯ«Ћ Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї | y | < 1 Я«јЯ«ЕЯ«хЯ»ЂЯ«│Я»ЇЯ«│ Я«јЯ«▓Я»ЇЯ«▓Я«Й y Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«цЯ»Ђ Я«фЯ»іЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»ЂЯ««Я»Ї. Я«фЯ«┐Я«ЕЯ»ЇЯ«фЯ»Ђ y -Я«ЋЯ»ЇЯ«ЋЯ»Ђ 3x Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ«┐Я«░Я«цЯ«┐Я«»Я«┐Я«Ъ, | 3 x | < 1 Я«јЯ«ЕЯ«хЯ»ЂЯ«│Я»ЇЯ«│ Я«јЯ«▓Я»ЇЯ«▓Я«Й x Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї 1/(1+3x)2 -Я«ЕЯ»Ї Я«хЯ«┐Я«░Я«┐Я«хЯ»Ђ Я«ЈЯ«▒Я»ЇЯ«фЯ»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. | x | < 1/3 Я«љ Я«еЯ«┐Я«▒Я»ѕЯ«хЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«»Я»ЂЯ««Я»Ї x -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Є Я«ЄЯ«еЯ»ЇЯ«ц Я«хЯ«┐Я«░Я«┐Я«хЯ»Ђ Я«фЯ»іЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»ЂЯ««Я»Ї.
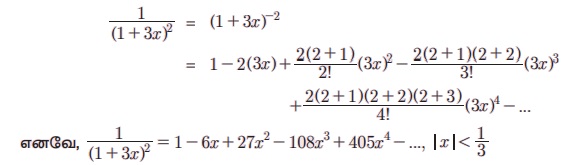
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.23 1/(3+2x)2 Я«љ x-Я«ЕЯ»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я«ЙЯ«Ћ Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«џЯ»єЯ«»Я»ЇЯ«Ћ. Я«ЁЯ«еЯ»ЇЯ«ц Я«хЯ«┐Я«░Я«┐Я«хЯ»Ђ Я«ЈЯ«▒Я»ЇЯ«фЯ»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«Е x -Я«ЕЯ»Ї Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ :
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«еЯ«ЙЯ««Я»Ї (1 + x)2-Я«ЕЯ»Ї Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«хЯ»ІЯ««Я»Ї.
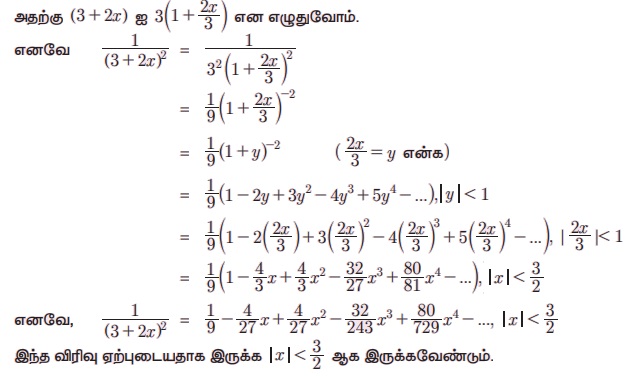
Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ Я««Я»ѓЯ«▓Я««Я»Ї, Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ««Я»ЇЯ«фЯ«ЪЯ«┐ Я««Я»ѓЯ«▓Я««Я»Ї Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я«хЯ»ѕЯ«ЋЯ«│Я»ѕ Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї. Я«ЁЯ«цЯ»Ђ Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ђЯ«┤Я»Є Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.24 ![]() -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
-Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ:
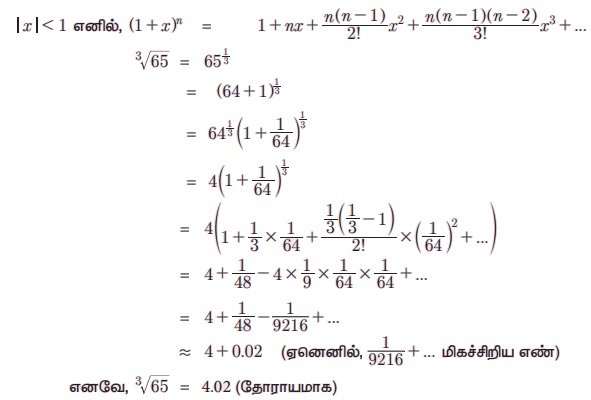
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 5.25 x Я«њЯ«░Я»Ђ Я«фЯ»єЯ«░Я«┐Я«» Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, 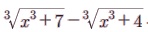 -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«цЯ»ІЯ«░Я«ЙЯ«»Я««Я«ЙЯ«Ћ 1/x2 Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
-Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«цЯ»ІЯ«░Я«ЙЯ«»Я««Я«ЙЯ«Ћ 1/x2 Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ :
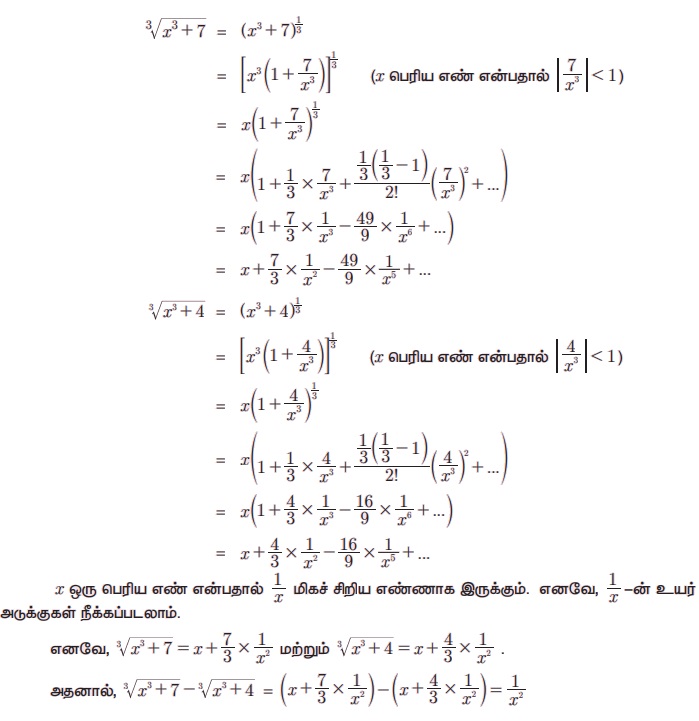
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ: Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»Ї n Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ѕЯ«░Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї Я«ЅЯ«БЯ»ЇЯ««Я»ѕ . Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, n = Рѕџ2
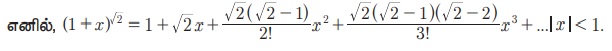
6. Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«▒Я«┐Я«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї (Exponential Series)
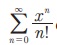 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«▒Я«┐Я«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї (Exponential Series) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»Ї x-Я«ЕЯ»Ї Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«▒Я«┐Я«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї (Exponential Series) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»Ї x-Я«ЕЯ»Ї Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ«▓Я«ЙЯ««Я»Ї.
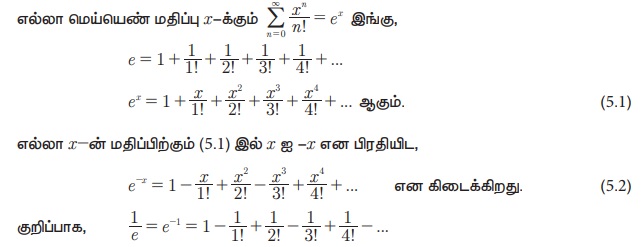
5.1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 5.2 Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕЯ«ЋЯ«│Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ
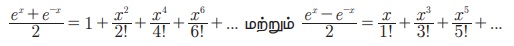
Я«јЯ«Е Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«Ћ,
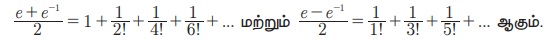
(5.1) Я«ЄЯ«▓Я»Ї x-Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«фЯ«цЯ«┐Я«▓Я«ЙЯ«Ћ 2 x Я«љ Я«фЯ«┐Я«░Я«цЯ«┐Я«»Я«┐Я«Ъ,
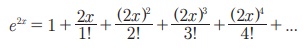
Я«џЯ»ЂЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»іЯ«┤Я»ЂЯ«цЯ»Ђ Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«цЯ»Ђ,
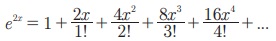
7. Я««Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї (Logarithmic Series)
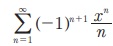 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї (Logarithmic Series) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»Ї | x | < 1 Я«јЯ«ЕЯ«хЯ»ЂЯ«│Я»ЇЯ«│ x -Я«ЕЯ»Ї Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ. x = 1-Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї (Logarithmic Series) Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»Ї | x | < 1 Я«јЯ«ЕЯ«хЯ»ЂЯ«│Я»ЇЯ«│ x -Я«ЕЯ»Ї Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ. x = 1-Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ.
| x | < 1 Я«јЯ«ЕЯ«хЯ»ЂЯ«│Я»ЇЯ«│ Я«јЯ«▓Я»ЇЯ«▓Я«Й x Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«еЯ»ЇЯ«ц Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї log(1+ x) Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї 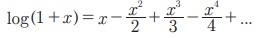
| x | < 1 Я«јЯ«ЕЯ«хЯ»ЂЯ«│Я»ЇЯ«│ Я«јЯ«▓Я»ЇЯ«▓Я«Й x Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї x -Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«фЯ«цЯ«┐Я«▓Я«ЙЯ«Ћ - x Я«јЯ«Е Я«фЯ«┐Я«░Я«цЯ«┐Я«»Я«┐Я«Ъ,
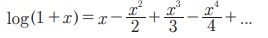 Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ.
Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ.
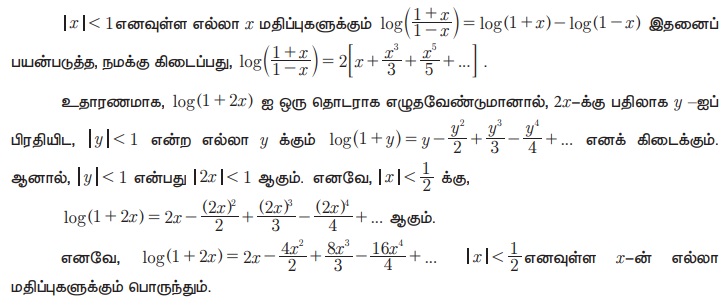
Я«фЯ«»Я«┐Я«▒Я»ЇЯ«џЯ«┐ 5.4
1. Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ«хЯ«ЕЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ x -Я«ЕЯ»Ї Я«ЈЯ«▒Я»ЂЯ«хЯ«░Я«┐Я«џЯ»ѕ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я«ЙЯ«Ћ Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«џЯ»єЯ«»Я»ЇЯ«Ћ. Я«ЁЯ«еЯ»ЇЯ«ц Я«хЯ«┐Я«░Я«┐Я«хЯ»Ђ Я«ЈЯ«▒Я»ЇЯ«фЯ»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«Е x - Я«ЕЯ»Ї Я«еЯ«┐Я«фЯ«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.

2. 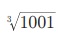 -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«цЯ»Ї Я«цЯ»ІЯ«░Я«ЙЯ«»Я««Я«ЙЯ«Ћ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. (Я«ЄЯ«░Я»Ђ Я«цЯ«џЯ««Я«цЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«цЯ»ЇЯ«цЯ««Я«ЙЯ«Ћ)
-Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«цЯ»Ї Я«цЯ»ІЯ«░Я«ЙЯ«»Я««Я«ЙЯ«Ћ Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. (Я«ЄЯ«░Я»Ђ Я«цЯ«џЯ««Я«цЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«цЯ»ЇЯ«цЯ««Я«ЙЯ«Ћ)
3. x Я«њЯ«░Я»Ђ Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я«ЁЯ«│Я«хЯ«┐Я«▓Я«ЙЯ«Е Я«фЯ»єЯ«░Я«┐Я«» Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, 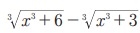 -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«цЯ»Ї Я«цЯ»ІЯ«░Я«ЙЯ«»Я««Я«ЙЯ«Ћ 1/ x2 Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
-Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«цЯ»Ї Я«цЯ»ІЯ«░Я«ЙЯ«»Я««Я«ЙЯ«Ћ 1/ x2 Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
4. x Я««Я«┐Я«ЋЯ«џЯ»Ї Я«џЯ«┐Я«▒Я«┐Я«»Я«цЯ»Ђ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, 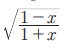 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ»ІЯ«░Я«ЙЯ«»Я««Я«ЙЯ«Ћ
Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ»ІЯ«░Я«ЙЯ«»Я««Я«ЙЯ«Ћ 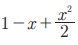 Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
5. Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«▒Я«┐Я«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«┐Я«▓Я»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї 6 Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. 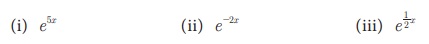
6. Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я««Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї 4 Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.

Я«ЄЯ«еЯ»ЇЯ«ц Я«хЯ«┐Я«░Я«┐Я«хЯ»ЂЯ«ЋЯ«│Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я«јЯ«еЯ»ЇЯ«ц Я«ЄЯ«ЪЯ»ѕЯ«хЯ»єЯ«│Я«┐Я«»Я«┐Я«▓Я»Ї Я«ЈЯ«▒Я»ЇЯ«фЯ»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ»Ђ Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ
7.  Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.
Я«јЯ«Е Я«еЯ«┐Я«▒Я»ЂЯ«хЯ»ЂЯ«Ћ.

Я«фЯ«»Я«┐Я«▒Я»ЇЯ«џЯ«┐ 5.5
Я«џЯ«░Я«┐Я«»Я«ЙЯ«Е Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я««Я«┐Я«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЈЯ«▒Я»ЇЯ«фЯ»ЂЯ«ЪЯ»ѕЯ«» Я«хЯ«┐Я«ЪЯ»ѕЯ«»Я»ѕЯ«цЯ»Ї Я«цЯ»ЄЯ«░Я»ЇЯ«цЯ»єЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
1. 2 + 4 + 6 +... + 2n -Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ

2. 
3. (2 x + 3y)20 Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«┐Я«░Я«┐Я«хЯ«┐Я«▓Я»Ї x8y12 -Я«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»Ђ

4. r-Я«ЕЯ»Ї Я«јЯ«▓Я»ЇЯ«▓Я«Й Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї nC10 > nCr Я«јЯ«ЕЯ«┐Я«▓Я»Ї, n-Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
(1) 10
(2) 21
(3) 19
(4) 20
5. Я«ЄЯ«░Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐ a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ g Я«јЯ«ЕЯ«┐Я«▓Я»Ї,
(1) a РЅц g
(2) a РЅЦ g
(3) a = g
(4) a > g
6. (1 +x2)2 (1 +x)n = a0 + a1x + a2x2 + ... + xn+4 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї a0, a1 , a2 Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, n-Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
(1) 1
(2) 5
(3) 2
(4) 4
7. a, 8, b Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ, a, 4, b Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї a, x, b Я«јЯ«ЕЯ»ЇЯ«фЯ«Е Я«ЄЯ«џЯ»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ Я«јЯ«ЕЯ«┐Я«▓Я»Ї, x-Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
(1) 2
(2) 1
(3) 4
(4) 16
8. 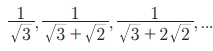 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ««Я»ЂЯ«▒Я»ѕ
(1) Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ
(2) Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ
(3) Я«ЄЯ«џЯ»ѕЯ«џЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ
(4) Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕ
9. Я«ЄЯ«░Я»Ђ Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є 16 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 8 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«ЄЯ«џЯ»ѕЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐
(1) 10
(2) 6
(3) 5
(4) 4
10. Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ««Я»Ї d Я«єЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Sn Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Sn - 2 Sn-1 + Sn-2 - Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
(1) d
(2) 2d
(3) 4d
(4) d2
11. 3815 Я«љ 13 Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»ђЯ«цЯ«┐
(1) 12
(2) 1
(3) 11
(4) 5
12. 1, 2, 4, 7, 11, Рђд Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї n Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ

13. 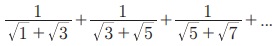 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї
14. 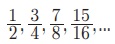 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї n Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«ЕЯ»Ї n Я«єЯ«хЯ«цЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ
(1) 2n РђЊ n - 1
(2) 1 РђЊ 2- n
(3) 2- n + n - 1
(4) 2 n-1
15. 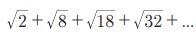 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї n Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї.
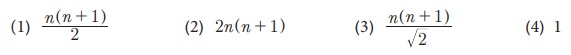
16. 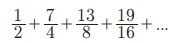 Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ
(1) 14
(2) 7
(3) 4
(4) 6
17. Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«┐Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ 18 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»Ђ 6 Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї

18. e-2x Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я«┐Я«▓Я»Ї x5 -Я«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»Ђ