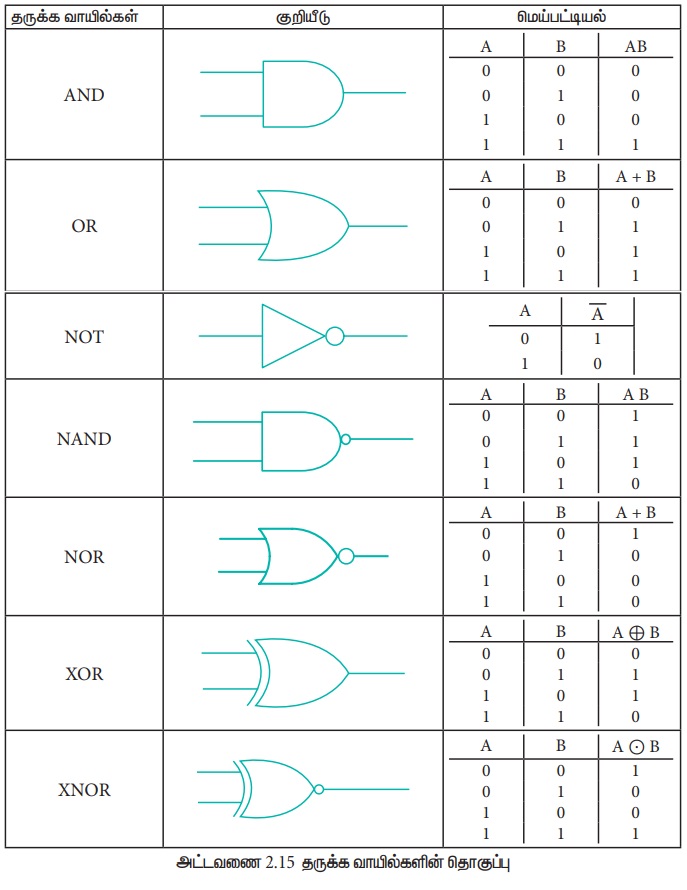
அடிப்படை தருக்க வாயில்கள்

அடிப்படை தருக்க வாயில்கள்:

தருக்க வாயில் என்பது அடிப்படை மின்னணு சுற்றாகும். இது ஒன்று அல்லது அதற்கு மேற்பட்ட சமிஞ்சைகளில் செயற்பட்டு ஒரு வெளியீட்டு சமிஞ்சைகள் தரும். மூன்று அடிப்படை வாயிலாக AND, OR மற்றும் NOT வாயில்கள் உள்ளன. NAND, NOR, XOR மற்றும் XNOR போன்ற வாயில்கள் அடிப்படை வாயில்களிலிருந்து தருவிக்கப்பட்டவை. NAND மற்றும் NOR வாயில்கள் பொதுமை வாயில்கள் (Universal gates) என்றழைக்கப்படும். அடிப்படை தருக்க வாயில்களை இவற்றின் மூலம் உருவாக்கலாம். 

1. AND வாயில்:

இரண்டு அல்லது அதற்கு மேலான உள்ளீட்டு சமிஞ்சைகளைக் கொண்டு செயற்பட்டு ஒரு வெளியீட்டு சமிஞ்சைகளை தரும்.

இரண்டு உள்ளீடுகளும் 'மெய்' எனில் மட்டுமே இதன் வெளியீடு ‘True' இருக்கும் அல்லது 'False’. அதாவது உள்ளீடுகள் அனைத்தும் 1 என்ற மதிப்பிலிருந்தால் இதன் வெளியீடு 1

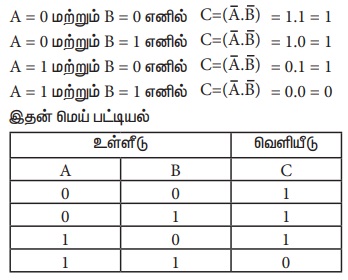
இரண்டு உள்ளீடுகளும் மெய்யெனில் மட்டுமே இதன் வெளியீடு மெய்யாக இருக்கும் அல்லது பொய்யாகிவிடும். அதாவது உள்ளீடுகள் அனைத்தும் 1 என்ற மதிப்பிலிருந்தால் இதன் வெளியீடு 1-ஆக இருக்கும் அல்லது 0 - ஆகிவிடும். A மற்றும் B என்ற மாறிகளில் உள்ளீட்டையும், C என்ற மாறியில் வெளியீட்டையும் அறிவித்தால், A மற்றும் B மாறிகள் 0 அல்லது 1 என்ற மதிப்பை ஏற்கும். AND வாயிலின் தருக்க குறி.

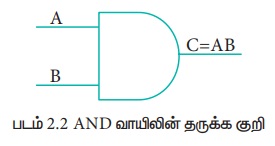
AND வாயிலின் செயற்பாட்டை C = A AND B என்ற பூலியன் செயற்பாட்டில் குறிப்பிடலாம்.

பூலியன் இயற்கணிதத்தில், பெருகல் குறி AND செயற்பாட்டை குறிக்கும். இதனால் AND வாயிலின் வெளியீடு

C = A.B   C = AB குறிக்கலாம். 

“C என்பது A AND B” என்று இதை படிக்கலாம். இரண்டு உள்ளீட்டு மாறிகளை கொண்டிருப்பதால் மொத்தம் நான்கு விதங்களில் உள்ளிடலாம். அவை 00,01,10 மற்றும் 11.

எடுத்துக்காட்டாக இரண்டு உள்ளீடுகளும் 0 எனில்,

C = A . B

= 0.0 

= 0

AND வாயிலின் மெய்பட்டியல் கீழே கொடுக்கப்பட்டுள்ளது.

2. OR வாயில்

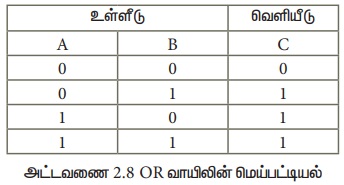
தருக்க OR செயற்குறியினைப் போன்று செயல்படுவதால் இந்தவாயில் OR வாயில் என்ற பெயர் பெற்றது. கொடுக்கப்பட்ட இரண்டு உள்ளீடுகளில் ஏதேனும் ஒன்று அல்லது இரண்டு உள்ளீடுகளுமே ‘மெய்’ என இருந்தால் மட்டுமே இவ்வாயில் ‘மெய்’ என வெளியீட்டை தரும். இரு உள்ளீடுகளும் ‘பொய்’ எனில், ‘பொய்’ என்றே வெளியீடு தரும். விதமாக சொல்வதனால், கொடுக்கப்பட்ட உள்ளீடுகளில் ஒன்று அல்லது இரண்டு உள்ளீடுகளும் 1 எனில் வெளியீடு 1 இல்லாவிடில் வெளியீடு 0 OR வாயிலின் தருக்க குறியீடு.

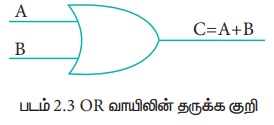
OR வாயிலின் வெளியீடு 

C = A OR B 

OR செயல்பாட்டை கூட்டல் குறி (+) பயன்படுத்தி குறிப்பிடலாம். எனவே,

C = A + B 

மேலே உள்ள சமன்பாட்டை C என்பது A அல்லது B என வாசிக்கலாம். 

எடுத்துக்காட்டாக, இரு உள்ளீடுகளும் 1 எனில்,

C = A + B = 1 + 1 = 1 

OR வாயில் மெய் பட்டியல் 

3. NOT வாயில்: 

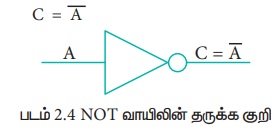
NOT வாயில் தருக்க தலைகீழி என அழைக்கப்படுகிறது. இது ஒரு உள்ளீட்டை மட்டுமே ஏற்கும். இது தருக்க நிலையை மாற்றும். வேறு வார்த்தைகளில் கூறவேண்டுமெனில், வெளியீடு C எப்பொழுதும் உள்ளீட்டின் தலைகீழாகவே இருக்கும். 

NOT வாயில் தருக்க குறியீடு வருமாறு

NOT வாயிலின் பூலியன் செயல்பாடு

C = NOT A 

பூலியன் இயற்கணிதத்தில், மேல்கோடு NOT செயல்பாட்டின் நிலையை குறிக்கும். எனவே

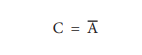
இதனை “C என்பது NOT A” அல்லது “C என்பது Aன் தலைகீழி” என வாசிக்கலாம்.

A ன் மதிப்பு 0 எனில்,  

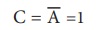
அல்லது A ன் மதிப்பு 1 எனில்,

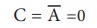
NOT வாயிலின் மெய் பட்டியல் வருமாறு

4. NOR வாயில்:

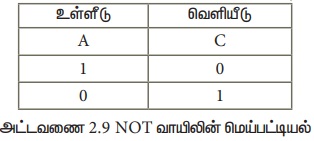
NOR வாயில் மின்னணு சுற்று, ஒரு OR வாயிலை தொடர்ந்து ஒரு தலைகீழி வாயிலை (NOT வாயில்) பொருத்தி உருவாக்கப்படும். கொடுக்கப்படும் இரண்டு உள்ளீடுகளும் பொய் எனில் மட்டுமே இவ்வாயில் மெய் என்ற வெளியீட்டை தரும். இல்லாவில் பொய் என்ற வெளியீட்டை தரும். வேறுவகையில் கூறுவதெனில், 1 என்பதை வெளியீடாக பெற, இரண்டு உள்ளீடுகளின் மதிப்பும் ) என்று இருக்க வேண்டும். இல்லாவில் அதன் வெளியீடு 0 ஆகும். 

NOR வாயிலின் தருக்க சுற்று

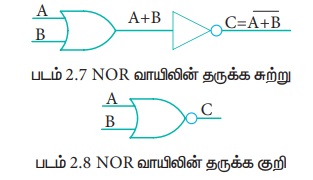
NOR வாயிலின் வெளியீடு

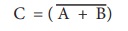
இதனை C என்பது A அல்லது மயின் இல்லை அல்லது C என்பது A அல்லது B யின் தலைகீழி என வாசிக்கலாம். 

எடுத்துக்காட்டாக,

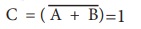
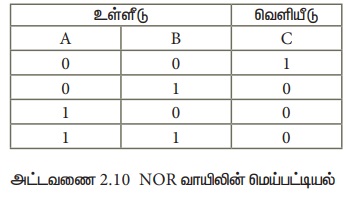
NOR வாயிலின் மெய் பட்டியல் 

5. வட்டமிட்ட AND வாயில் (Bubbled AND gate):

வட்டமிட்ட AND வாயிலின் தருக்க சுற்று கீழே கொடுக்கப்பட்டுள்ளது.

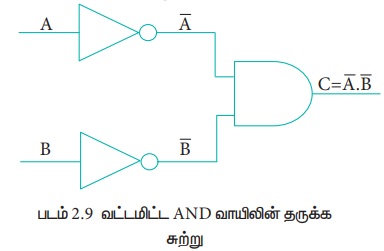
மேலே கொடுக்கப்பட்ட சுற்றில் உள்ளீட்டுக்களின் மதிப்பை தலைகீழாக மாற்றி AND வாயில் எடுத்துக் கொண்டு வெளியீட்டை

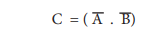என்று தரும்.

உள்ளீட்டுகளுக்கு வட்டமிடுவதன் மூலம். இந்த சுற்றை கீழே கொடுக்கப்பட்டுள்ளது போல மாற்றி வரையலாம், இதில் வட்டங்கள் தலைகீழ் என்று குறிக்கும்.

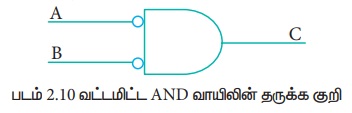
இந்த தருக்க சுற்றின் வெளியீட்டை எல்லா உள்ளீட்டின் மதிப்புகளைக் கொண்டு ஆராய்ந்தால்,

வட்டமிட்ட AND வாயிலின் வெளியீடும் NOR வாயிலின் வெளியீடும் ஒன்றாகயிருக்கும். NOR வாயிலை வட்டமிட்ட AND வாயிலின் மூலம் குறிப்பிடலாம். மாறாக இவ்விரண்டு வாயிலில்களும் ஒன்றோடு ஒன்று மாற்றியமைக்கலாம். 

எனவே,

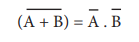
இந்த சமன்பாடு டீமார்கன் தேற்றத்தின் முதலாம் விதியை நிறுவும்

6. NAND வாயில்:

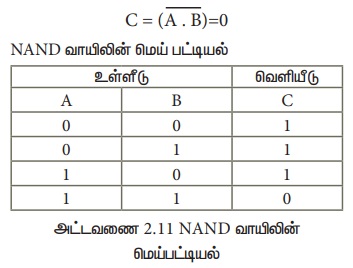
AND வாயிலின் வெளியீட்டை NOT வாயிலுக்கு அனுப்பி பெறும் வெளியீட்டை கொண்டு NAND வாயில் செயற்படும். இதன் தருக்க செயற்பாடு AND வாயிலின் வெளியீட்டை தலைகீழாக பெறும், உள்ளீடுகள் அனைத்தும் "மெய்" எனில், இதன் வெளியீடு "பொய்" ஆகயிருக்கும், இல்லையேல் இதன் வெளியீடு "மெய்” ஆகயிருக்கும். மாறாக உள்ளீட்டுக் அனைத்தும் 1 எனில் NAND வாயிலின் வெளியீடு 0- ஆகயிருக்கும், இல்லையேல் இதன் வெளியீடு 1-ஆகயிருக்கும். NAND வாயிலின் தருக்க சுற்று.

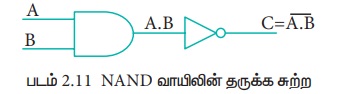
NAND வாயிலின் தருக்க குறி கீழே கொடுக்கப்பட்டுள்ளது.

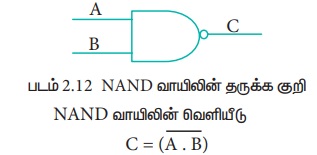
இதனை இதனை C என்பது A மற்றும் B யின் இல்லை அல்லது C என்பது A மற்றும் B யின் தலைகீழி என வாசிக்கலாம்.

எடுத்துக்காட்டாக, இரண்டு உள்ளீடுகளும் 1 எனில்.

7. வட்டமிட்ட OR வாயில்:

வட்டமிட்ட OR வாயில் தருக்க சுற்று கீழே கொடுக்கப்பட்டுள்ளது.

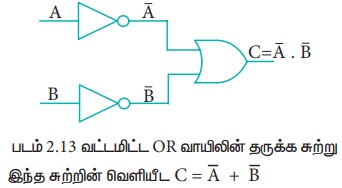
என்று எழுதலாம். உள்ளீட்டுகளுக்கு வட்டமிட்ட, மேலே உள்ள சுற்றை இவ்வாறு வேறு விதமாக வரையலாம், இதில் வட்டங்கள் தலைகீழ் என்பதை குறிக்கும்.

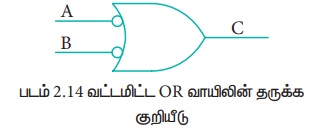
வட்டமிட்ட OR வாயிலின் மெய்பட்டியல் கீழே கொடுக்கப்பட்டுள்ளது. 

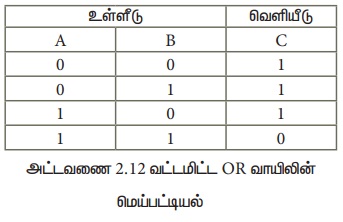
வட்டமிட்ட OR வாயில் மற்றும் NAND வாயிலின் மெய்பட்டியல்களை ஒப்பீடு செய்தால் இரண்டும் ஒன்றாகவே இருக்கும். ஆகவே இவ்விரண்டு சுற்றுகளும் ஒன்றிலிருந்து இன்னொன்றாக மாற்றியமைக்கலாம்.

அதாவது,

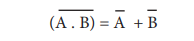
இது டிமார்கனின் (De-Morgan) இரண்டாவது தேற்றத்தை நிரூபிக்கிறது. 

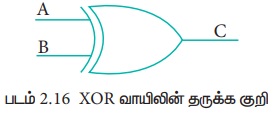
8. XOR வாயில்:

என்பது (Exclusive OR) வாயில், இது தருக்க "either/OR" என்பது போலவே செயல்படும்.

ஏதேனும் ஒன்று அல்லது அனைத்து உள்ளீடுகளும் "மெய்" எனில், இதன் வெளியீடு "மெய்" ஆகும். உள்ளீடுகள் "மெய்" அல்லது "பொய்" என்றிருந்தால், இதன் வெளியீடு "மெய்" ஆகும். அதாவது, உள்ளீடுகளின் மதிப்பு வேவ்வேறாக இருந்தால், வெளியீடு 1-ஆகயிருக்கும் அல்லது உள்ளீடுகள் ஒரே மதிப்பிலிருந்தால் வெளியீடு 0- ஆகும். XOR வாயிலின்தருக்க சுற்று கீழே கொடுக்கப்பட்டுள்ளது.

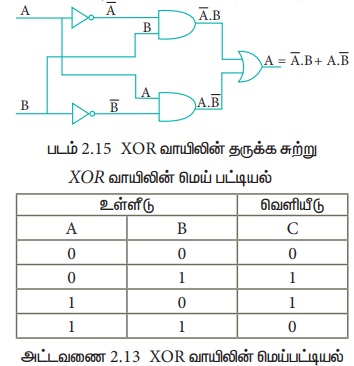
Exclusive OR செயற்பாட்டை, பூலியன் கணிதத்தில் சுழிக்குள் உள்ள கூட்டல் குறி மூலம் அல்லது இதை "Encircled Plus” என்று குறிப்பிடலாம்.

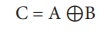
XOR வாயிலின் தருக்க குறி கீழே கொடுக்கப்பட்டுள்ளது.

9. XNOR வாயில்:

XNOR (Exclusive --NOR) வாயில் என்பது XOR வாயில் இருந்து வந்த வெளியீட்டினை, தலைகீழாக மாற்றி தரும். இரு உள்ளீடுகளும் சமமாக இருக்கும் போது இதன் வெளியீடு "மெய்" ஆகயிருக்கும், அல்லது உள்ளீடுகள் வேவ்வேறாக இருப்பின் வெளியீடு "பொய்" ஆகயிருக்கும். மாறாக உள்ளீடுகள் சமம். எனில் வெளியீடு 1-ஆகயிருக்கும், இல்லையேல் வெளியீடு 0 -ஆகும்.

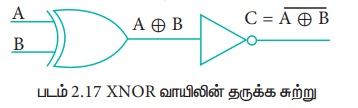
XNOR வாயிலின் வெளியீடு, XOR வாயிலின் வெளியீட்டை NOT வாயிலுக்கு செலுத்தி பெறப்படும்.

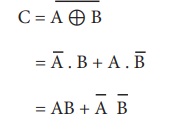
பூலியன் கணிதத்தில், சுழிக்குள் புள்ளி அல்லது "included dot” என்பதை குறிக்கும்.

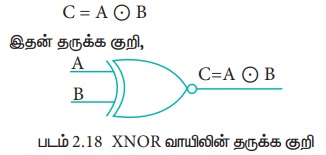
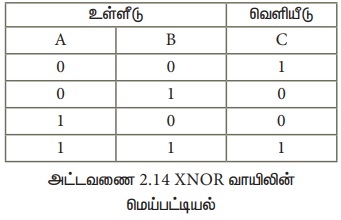
XNOR வாயிலின் மெய்பட்டியல் கீழே கொடுக்கப்பட்டுள்ளது. 

இந்த ஏரண வாயில்களைப் பயன்படுத்தி, சிக்கலான பல சுற்றுகளை உருவாக்கலாம். ஒரு சில்லில் எத்தனை வாயில்களை வைக்கலாம் என்பதற்கு மேல் வரம்பு குறிக்கும் கருத்தியல் ஏதுமில்லை. ஆனால் நடைமுறையில், கொடுக்கப்பட்ட சில்லுவின் அமைப்பிடத்தில், எத்தனை வாயில்கள் அமைக்க முடியும் என்பதன் எண்ணிக்கைக்கு வரம்புள்ளது. தருக்க வாயில்களின் அணியை எண்ணளவு ஒருங்கிணைந்த சுற்றுகளில் (Digital Integrated Circuits) காணப்படும்.