பூலியன் இயற்கணிதம்

பூலியன் இயற்கணிதம்

அறிமுகம்:

பூலியன் இயற்கணிதம் ஒரு இலக்க வகை கணினியில், இலக்க சுற்றுகளை வடிவமைக்கப் பயன்படுத்தப்படும் ஒரு கணித ஒழுக்கமாகும். இது இலக்க சுற்றுகளில் உள்ள உள்ளீடுகள் மற்றும் வெளியீடுகளுக்கு இடையே உள்ள உறவை விவரிக்கிறது. பூலன் இயற்கணிதத்தின் அடிப்படைக் கொள்கைகளை ஆங்கிலேய கணிதவியலாளரான ஜார்ஜ் பூல் (George Boole) என்பவரால் முன்மொழியப்பட்டது, அவரை கௌரவிக்கும் வகையில் இதற்கு பூலியன் இயற்கணிதம் என்று பெயர் சூட்டப்பட்டது.

உங்களுக்கு தெரியுமா?

ஜார்ஜ் பூல் (1815 - 1864) குறைந்த வருமானம் உள்ள குடும்பத்தில் பிறந்த இவர் ஆரம்ப பள்ளி கல்வி மட்டுமே முடித்திருந்தாலும், யாருடைய உதவியின்றி தானாகவே உயர் கணித கோட்பாடுகளை கற்று அறிந்தார். மேலும் பல மொழிகளிலும் இளமையிலோயே தேர்ச்சிப் பெற்றிருந்தார். பதினாறு வயதிலேயே கல்வி பணியை துடக்கி, பத்தொன்பது வயதில் தனது சொந்த பள்ளியை தொடங்கினார். அவருடைய இருபது வயது காலகட்டத்தில் உள்ள முக்கிய கணிதக் கோட்பாடுகளில் தேர்ச்சி பெற்றவராய் திகழ்ந்தவர் இவர்.

1. இரும மதிப்பு அளவுகள்:

ஒவ்வொரு நாளும் நாம் தருக்கரீதியான முடிவுகளை எடுக்க வேண்டியுள்ளது:

1. கணிப்பொறியில் பாடபுத்தகத்தை அன்றாடம் பள்ளிக்கு கொண்டு செல்ல வேண்டுமா? ஆம் / இல்லை

2. 8-10=10 இந்த பதில் சரியா? - ஆம் / இல்லை 

3. சென்னை, இந்தியாவின் தலைநகரம்? ஆம் / இல்லை

4. நேற்று நான் என்ன சொன்னேன்?

மேற்கண்ட கேள்விகளில் முதல் மூன்றுக்கு பதில் மெய் (ஆம்) அல்லது பொய் (தவறு) என்றிருக்கும். ஆனால் நான்காவது கேள்வியின் பதில் சரி அல்லது தவறு என்று கூறமுடியாது. ஆதலால், மெய் அல்லது பொய் என்று தீர்மானிக்கப்படக்கூடிய வாக்கிங்களை “தருக்கரீதியான அறிக்கைகள்" (Logical Statement) அல்லது “உண்மை செயல்பாடுகள்” (Truth functions) என்று அழைக்கப்படுகின்றன. மெய் அல்லது பொய் என்ற முடிவுகளை “உண்மை மதிப்புகள்” (Truth values) எனப்படும். தருக்கரீதியான மாறிலி 1 மற்றும் 0 மூலம் வரையறுக்கப்பட்ட உண்மை மதிப்புகளாகும்; இதில் 1 என்பது மெய், 0 என்பது பொய்யைக் குறிக்கும். உண்மை மதிப்புகளை சேமிக்க உதவும் மாறியை “இரும மதிப்பு மாறிகள்” (Binary valued variables) அல்லது “பூலியன் மாறிகள்” (Boolean Variables) என்றழைக்கப்படுகின்றன. ஏன் என்றால் இவ்வகை மாறியில் மெய் அல்லது பொய் என்ற இரண்டில் ஏதேனும் ஒரு மதிப்பை தான் சேமிக்க முடியும்.

2. தருக்க செயற்பாடுகள்:

பூலியன் இயற்கணிதம் மாறிகள் மற்றும் பல்வேறு செயற்பாடுகள் (சார்புகள்) கொண்டது. AND, OR மற்றும் NOT போன்ற அடிப்படை தருக்க செயற்பாடுகள் முறையே புள்ளி (.), கூட்டல் குறி (+) மற்றும் மேல்கோடு அல்லது அபாஸ்ட்ரஃபி குறி என்பவற்றால் குறிப்பிடலாம். இந்த குறிகளை "தருக்க செயற்குறிகள்” என்றழைக்கப்படும்.

3. மெய் பட்டியல்:

தருக்க மாறி அல்லது தருக்க அறிக்கையில் உள்ள எல்லா மெய் மதிப்புகளின் முடிவுகள் மெய் பட்டியலில் அமைக்கப்படும். AND செயற்குறியின் மெய்பட்டியல் கீழே கொடுக்கப்பட்டுள்ளது.

4. AND செயற்குறி:

பூலியன் இயற்கணிதத்தில் புள்ளி (.) குறியுடன் AND செயற்குறியை குறிப்பிடலாம். சாதாரண இயற்கணித பெருக்களுக்கு இணையானது இரண்டு அல்லது அதற்கு மேற்பட்ட உள்ளீட்டு மாறிகளை இணைத்து AND செயற்குறி வெளியீட்டை தரும், அனைத்து உள்ளீடுகளும் மெய்' ஆகயிருந்தால் மட்டுமே வெளியீடு மெய்யாக இருக்கும். 2- உள்ளீட்டு AND செயற்குறியின் மெய்பட்டியல் கீழே கொடுக்கப்பட்டுள்ளது.

இந்த 2-உள்ளீடுகளை கொண்ட AND இயக்கத்தின் தொடரை Y = A . B என எழுதலாம். 

5. OR செயற்குறி:

OR செயற்குறி கூட்டல் குறியுடன் (+) குறிப்பிடலாம். இரண்டு அல்லது இரண்டிற்கு மேற்பட்ட உள்ளீடுட்டு மாறிகளின் மதிப்பை இணைத்து OR செயற்குறி வெளியீட்டை தரும். ஏதேனும் ஒரு உள்ளீடு மெய் (1) என்று கொடுக்கும். 2 - உள்ளீட்டிற்கான OR செயற்குறியின் மெய்ப் பட்டியல் கீழே கொடுக்கப்பட்டுள்ளது.

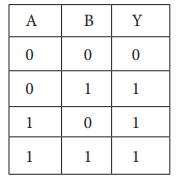
இரு மாறிகளைக் கொண்ட இந்த பூலியன் தொடரை Y = A + B என எழுதலாம். 

6. NOT செயற்குறி:

NOT செயற்குறி ஒரு உள்ளீடை மற்றும் ஏற்று அதற்கான வெளியீட்டை தரும். மெய் அல்லது பொய்யாக இருக்கும் உள்ளீட்டிற்கு அதன் நேர்மறையான வெளியீட்டை NOT செயற்குறி கொடுக்கும். அதாவது NOT செயற்குறி உள்ளீட்டின் மதிப்பை தலைகீழாக கொடுக்கும்.

A என்ற உள்ளீட்டு மாறி மற்றும் Y என்ற வெளியீட்டுடன் கூடிய NOT செயற்குறியின் மெய் பட்டியல் கீழே கொடுக்கப்பட்டுள்ளது.

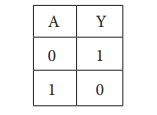
Y = என்ற பூலியன் வெளிப்பாடு மூலம் NOT செயற்குறியை இயற்கணிதத்தில் குறிப்பிடலாம். 

எடுத்துக்காட்டு:

கீழே கொடுக்கப்பட்டுள்ள பூலியன் சமன்பாட்டை கருத்தில் கொண்டால்: 

A = 1 என்ற மதிப்பு கொண்டிருக்கும்போதோ அல்லது (B = 0, C = 1) என்ற மதிப்புகளை கொண்டிருக்கும் போது) என்ற மதிப்பு கொண்டால், D-யில் உள்ள மதிப்பு 1 (மெய்) ஆக இருக்கும். இல்லையேல் D-ல் 0 (பொய்) என்ற மதிப்பு கொண்டிருக்கும்.

AND, OR மற்றும் NOT போன்ற அடிப்படை தருக்க செயற்பாடுகளை இணைத்து NAND மற்றும் NOR போன்ற தருக்க செயற்குறிகளை உருவாக்கலாம்.

7. NAND செயற்குறி:

NAND என்பது AND மற்றும் NOT என்பதன் தொகுப்பாகும். AND செயற்குறியின் வெளியீட்டை தலைகீழாக அமைத்தால் NAND செயற்குறியின் வெளியீட்டை பெறலாம். NAND செயற்பாட்டை, இயற்கணித கூற்றாக

Y = A . B எனக் குறிப்பிடலாம் 

NAND B = NOT (A AND B) 

8. NOR செயற்குறி:

Y = A + B எனக் குறிப்பிடலாம் NOR செயற்பாட்டின் மெய்பட்டியல் கீழே கொடுக்கப்பட்டுள்ளது.

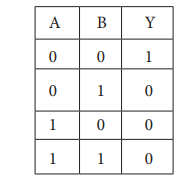
A NOR B = NOT (A OR B)