பருவம் 1 அலகு 3 | 6 ஆம் வகுப்பு கணக்கு - சமான விகிதங்கள் மற்றும் விகிதங்களை ஒப்பிடுதல் | 6th Maths : Term 1 Unit 3 : Ratio and Proportion
6 ஆம் வகுப்பு கணக்கு : பருவம் 1 அலகு 3 : விகிதம் மற்றும் விகித சமம்
சமான விகிதங்கள் மற்றும் விகிதங்களை ஒப்பிடுதல்
5. சமான விகிதங்கள்
தொகுதி மற்றும் பகுதியை ஒரே எண்ணால் பெருக்கவோ அல்லது வகுக்கவோ செய்தால் சமான விகிதங்களைப் பெறலாம். கீழ்க்கண்ட எடுத்துக்காட்டின் மூலம் இதனைப் புரிந்துகொள்ளலாம், கீழே கொடுக்கப்பட்ட செவ்வகங்களின் அகலம் மற்றும் நீளத்திற்கு இடையேயுள்ள விகிதங்களைக் காண்க.
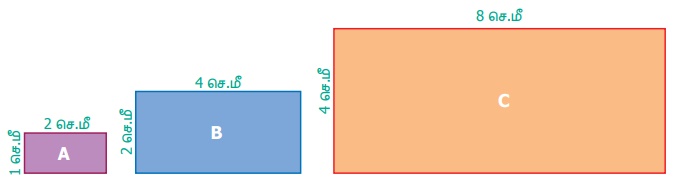
● செவ்வகம் (A) இன் அகலம் மற்றும் நீளங்களின் விகிதம் 1 : 2
● செவ்வகம் (B) இன் அகலம் மற்றும் நீளங்களின் விகிதம் 2 : 4 (எளிய வடிவம் 1 : 2)
● செவ்வகம் (C) இன் அகலம் மற்றும் நீளங்களின் விகிதம் 4 : 8 (எளிய வடிவம் 1 : 2)
● இங்கு, A, B மற்றும் C ஆகிய செவ்வகங்களின் அகலம் மற்றும் நீளங்களின் விகிதங்கள் சமான விகிதங்களாகும்.
● அதாவது, 1 : 2, 2 : 4 மற்றும் 4 : 8 ஆகியவை சமான விகிதங்களாகும்.
இவற்றை முயல்க
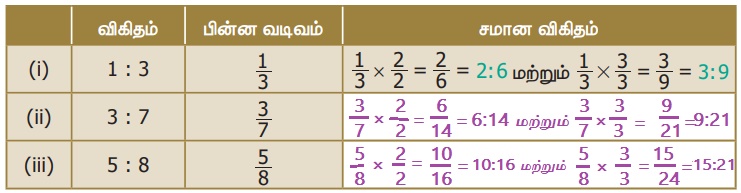
1. கீழேக் கொடுக்கப்பட்ட விகிதங்களுக்கு இரண்டு சமான விகிதங்கள் காண்க மற்றும் அட்டவணையை நிரப்புக.
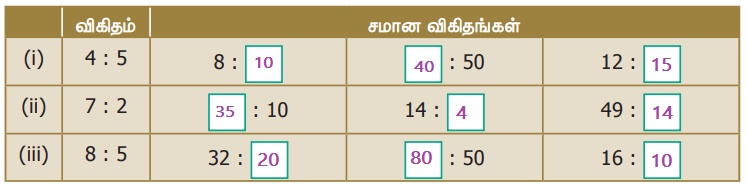
2. கொடுக்கப்பட்ட விகிதங்களுக்கு மூன்று சமான விகிதங்களைக் கண்டறிந்து பெட்டிகளில் நிரப்புக.
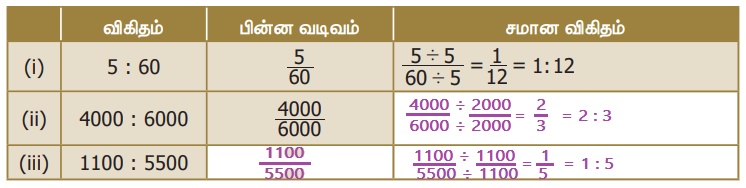
3. கீழேக் கொடுக்கப்பட்ட விகிதங்களுக்கு எளிய வடிவத்தைக் கண்டு அட்டவணையை நிரப்புக.
6. விகிதங்களை ஒப்பிடுதல்
கீழ்க்கண்ட சூழ்நிலைகளை எடுத்துக்கொள்வோம்.
சூழ்நிலை 1

(அ) இட்லி மாவில், உளுந்தம் பருப்பு மற்றும் அரிசிக்கு இடையேயுள்ள விகிதம் 1 : 4

(ஆ) இட்லி மாவில், உளுந்தம் பருப்பு மற்றும் அரிசிக்கு இடையேயுள்ள விகிதம் 1 : 3
இவற்றில் (படம் 3.2) எது பெரிய விகிதம் எனக் காண முடியுமா?
கொடுக்கப்பட்ட விகிதங்களைப் பின்ன வடிவில் எழுதி, ஒரே பகுதியுடைய சமானப் பின்னங்களாக மாற்றிய பிறகு தொகுதியை ஒப்பிட்டு எது பெரியது எனக் கூற இயலும்.
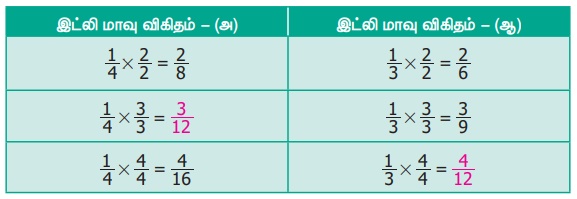
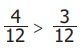 என்ற சமானப் பின்னத்திலிருந்து 1: 4 ஐ விட 1: 3 பெரியது என அறிய முடியும்.
என்ற சமானப் பின்னத்திலிருந்து 1: 4 ஐ விட 1: 3 பெரியது என அறிய முடியும்.
சூழ்நிலை 2
வேறு ஒரு சூழ்நிலையை எடுத்துக்கொள்வோம். எடுத்துக்காட்டாக, 5 மீ நீளமுள்ள நூலை 3 மீ மற்றும் 2 மீ நீளம் கொண்டதாக வெட்டினால், அத்துண்டுகளின் நீளங்களுக்கு இடையே உள்ள விகிதம் 3 : 2. இதிலிருந்து விகிதம் 'a : b' இல் 'a + b' பங்குகள் உள்ளன எனக் கூற முடியும்.
எடுத்துக்காட்டு 3.5
குமரனிடம் ₹600 உள்ளது. அதனை விமலாவிற்கும் யாழினிக்கும் 2 : 3 என்ற விகிதத்தில் பகிர்ந்தளிக்கிறார். இருவரில் யாருக்கு அதிகத் தொகை கிடைக்கும்? எவ்வளவு?
தீர்வு
மொத்தத் தொகையை 2 + 3 = 5 எனச் சமப் பாகங்களாகப் பிரிக்க வேண்டும். விமலாவிற்கு 5 இல் 2 பங்கும் யாழினிக்கு 5 இல் 3 பங்கும் உள்ளதாகப் பகிர்ந்தளிக்க வேண்டும்.
விமலாவிற்குக் கிடைக்கும் தொகை = ₹600 × ![]() = ₹240
= ₹240
யாழினிக்குக் கிடைக்கும் தொகை = ₹600 × ![]() = ₹360
= ₹360
விமலாவிற்கு ₹240 உம் யாழினிக்கும் ₹360 உம் கிடைக்கும். எனவே, விமலாவை விட யாழினிக்கு ₹120 அதிகமாகக் கிடைக்கும்.