நிகழ்வெண் பரவல் அட்டவணை

நிகழ்வெண் பரவல் அட்டவணை

நிகழ்வெண் பரவல்:

நிகழ்வெண் பரவல் என்பது கொடுக்கப்பட்டத் தரவுகளை அட்டவணை வடிவில் ஒவ்வொரு மாறிக்கும் நிகழ்வெண்ணை வரிசைப்படுத்துதலே ஆகும்.

இரண்டு வகையான நிகழ்வெண் பரவல் அட்டவணை முறைகள் உள்ளது. அவை

(i) தொகுக்கப்படாதத் தரவுகளுக்கு நிகழ்வெண் பரவல் அட்டவணை.

(ii) தொகுக்கப்பட்டத் தரவுகளுக்கு நிகழ்வெண் பரவல் அட்டவணை.

குறிப்பு

வீச்சு:

கொடுக்கப்பட்ட தரவுகளில் மிகப்பெரிய மதிப்புக்கும், மிகச்சிறிய மதிப்புக்கும் இடைப்பட்ட வித்தியாசம் வீச்சு ஆகும். தரவுகள் 5, 15, 10, 20 மற்றும் 18 எனில், வீச்சு = 20 − 5 = 15 ஆகும்.

இவற்றை முயல்க

1. கொடுக்கப்பட்டத் தரவுகளை ஏறு வரிசை மற்றும் இறங்கு வரிசையில் அமைக்க:  9,34,4,13,42,10,25,7,31,4,40 

2. கொடுக்கப்பட்டத் தரவுகளுக்கு வீச்சைக் காண்க 53, 42, 61, 9, 39, 63, 14, 20, 06, 26, 31, 4, 57

1. தொகுக்கப்படாத தரவுகளுக்கு நிகழ்வெண் பரவல் அட்டவணைத் தயாரித்தல் 

தொகுக்கப்படாதத் தரவுகள் அல்லது தனித்தத் தரவுகள்:

ஒரு தொகுக்கப்படாதத் தரவுகள் என்பது முழு எண்ணும் அறுதியிட்ட அளவும் ஆகும். இவ்வகையான தரவுகளுக்கு வீச்சு மதிப்புகள் இருக்காது. செவ்வகப்பட்டை விளக்கப்படம் மூலம் இதனை வழக்கமான வழியில் குறிக்கலாம். 

எடுத்துக்காட்டு: 1. ஒரு பள்ளியிலுள்ள ஆசிரியர்களின் எண்ணிக்கை

2. ஒரு விளையாட்டில் பங்கேற்கும் விளையாட்டு வீரர்களின் எண்ணிக்கை

எடுத்துக்காட்டு 6.1 

நான்காம் வகுப்பு படிக்கும் 25 மாணவர்களின் எடைகள் கீழேக் கொடுக்கப்பட்டுள்ளது. தொகுக்கப்படாத நிகழ்வெண் பரவல் அட்டவணையைத் தயாரித்து கீழ்க்காணும் வினாக்களுக்கு விடையளிக்க.

25, 24, 20, 25, 16, 15, 18, 20, 25, 16, 20, 16, 15, 18, 25, 16, 24, 18, 25, 15, 27, 20, 20, 27, 25.

 (i) மாணவர்களுடைய எடையின் வீச்சு காண்க.

 (ii) அதிகபட்ச எடை அளவு உள்ள மாணவர்களின் எண்ணிக்கை எத்தனை? 

(iii) அதிகபட்சமான மாணவர்கள் எந்த எடைப் பிரிவின் கீழ் வருகிறார்கள்?

(iv) குறைந்த எடையளவுள்ள மாணவர்களின் எண்ணிக்கை யாது? 

தீர்வு :

நிகழ்வுப் பரவல் அட்டவணையைத் தயாரிக்கவும். கொடுக்கப்பட்டத் தரவுகளை எடைக் கலத்திற்குக் கீழ் ஏறுவரிசையில் வரிசைப்படுத்த வேண்டும். பிறகு ஒவ்வொரு தரவுக்கும் நேரெதிரே நேர்க்கோட்டுக் குறிகள் கலத்திற்குக் கீழ் ஒரு நேர்க்கோடு இடுக. மேலும் ஒவ்வொரு மாறிகளுக்கான நேர்க்கோட்டுக் குறிகளின் எண்ணிக்கையை நிகழ்வெண் கலத்தில், கீழே கொடுக்கப்பட்டது போல் குறிக்கவேண்டும்.

எனவே, நிகழ்வெண் பரவல் அட்டவணை

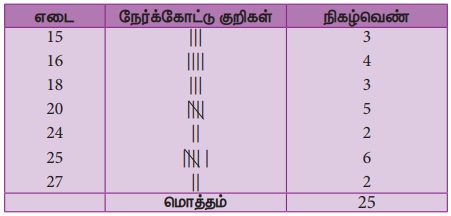
(i) கொடுக்கப்பட்டத் தரவுகளின் வீச்சு என்பது மிகப் பெரிய மற்றும் மிகச் சிறிய மதிப்புகளின் வித்தியாசம் ஆகும். இங்கு வீச்சு = 27−15 =12 ஆகும். 

(ii) இந்த அட்டவணையிலிருந்து, அதிகபட்ச எடை 27கி.கி உள்ள மாணவர்கள் 2 பேர். 

(iii) அதிகபட்சமாக 25 கி.கி எடையில் 6 மாணவர்கள் உள்ளனர். 

(iv) மிகக் குறைந்த எடை அளவான 15 கி.கி உள்ள மாணவர்கள் 3 பேர்.

எனவே, கொடுக்கப்பட்டத் தரவுகளை அட்டவணைப்படுத்த. ஒரே பார்வையில் விவரங்களை நாம் எளிதாகப் பெறமுடியும். இல்லையா?

செயல்பாடு 

1. உன் வகுப்புத் தோழர்களின் இரத்த வகைகளைச் சேகரிக்க. அட்டவணையை நிறைவு செய்து விவாதிக்க. 

2. உன் வகுப்புத் தோழர்களின் பெயர்களிலுள்ள கடைசி எழுத்தை உற்றுநோக்கி, அட்டவணைப்படுத்திப் பிறகு கீழ்க்காணும் வினாக்களுக்கு விடையளிக்க. 

1. பெயர்களில் எந்த எழுத்து அதிகமுறை கடைசி எழுத்தாக வந்துள்ளது? 

2. பெயர்களில் எந்த எழுத்து குறைந்தமுறை கடைசி எழுத்தாக வந்துள்ளது?

3. எந்தெந்த எழுத்துகள் பெயர்களின் கடைசி எழுத்தாக வரவில்லை ? 

4. சிறுமிகளின் பெயர்கள் அதிகமாக …………. என்ற எழுத்தில் முடிந்துள்ளது. 

5.  சிறுவர்களின் பெயர்கள் அதிகமாக …………….  என்ற எழுத்தில் முடிந்துள்ளது.

2. தொகுக்கப்பட்டத் தரவுகளுக்கு நிகழ்வெண் பரவல் அட்டவணையைத் தயாரித்தல் 

தொகுக்கப்பட்டத் தரவுகள் அல்லது தொடர்ச்சியானத் தரவுகள்:

தொகுக்கப்பட்டத் தரவுகள் என்பது குறிப்பிட்ட இடைவெளியில் அமைந்த மதிப்புகள் ஆகும். இந்தத் தரவுகள் மிகப் பெரிய மற்றும் மிகச் சிறிய மதிப்புடன் ஒரு குறிப்பிட்ட வீச்சில் அமையும். தொடர்ச்சியானத் தரவுகளை அட்டவணைப்படுத்துவதை நிகழ்வெண் பரவல் என அழைக்கின்றோம். நிகழ்வுச் செவ்வகத்தைப் பயன்படுத்தி இவற்றை வரைபடத்தின் மூலம் குறிக்கலாம்.

 எடுத்துக்காட்டு: 1. ஒரு கிராமத்தில் வசிப்பவர்களின் வயது.

2. உன் வகுப்பறையில் உள்ள மாணவர்களின் உயரம் மற்றும் எடை 

இப்பொழுது நாம் ஒரு சூழ்நிலையைக் கருதுவோம். 50 மாணவர்களின் மதிப்பெண்களைச் சேகரித்துள்ளதாகக் கொள்வோம். இந்த 50 மாணவர்களின் ஒவ்வொரு மதிப்பெண்ணுக்கும் நேராக நேர்க்கோட்டுக்குறிகள் இடுவது மிகக் கடினம். ஏனெனில், இந்த மதிப்பெண்களை அட்டவணைப்படுத்தினால் மிக நீளமாக இருக்கும் என்பதோடு விரைவாகப் புரிந்துகொள்ளவும் முடியாது. இதனால் நாம் பிரிவு இடைவெளியைப் பயன்படுத்துகிறோம். இந்த அட்டவணையில் கொடுக்கப்பட்டத் தரவுகளின் தொகுப்பைப் பிரிவு இடைவெளி முறையில் எழுதி நிகழ்வெண்ணைக் குறிக்க வேண்டும்.

பிரிவு இடைவெளி:

மாறிகளின் தொகுப்பு பிரிவுகளாகத் தொகுக்கப்பட வேண்டும். மேலும், ஒவ்வொரு தொகுப்பும் பிரிவு இடைவெளி (C.I) எனப்படும். ஒவ்வொரு பிரிவின் மேல் எல்லை மற்றும் கீழ் எல்லையின் வித்தியாசம் பிரிவு அளவு ஆகும். 

பிரிவு இடைவெளி (C.I) = மேல் எல்லை − கீழ் எல்லை

எடுத்துக்காட்டாக,

மதிப்பெண்களின் பிரிவு இடைவெளி 10 லிருந்து 20 என்பதை 10−20 என எழுதலாம். இதன் பிரிவு அளவு 20−10 =10.

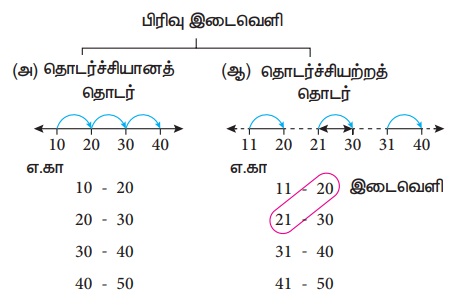
(அ) நிகழ்வெண் பரவலின்போது, கீழ்க்காணுமாறு எண்ணுதலைப் பின்பற்ற வேண்டும் 10−20, 20−30, 30−40..... ஆகியவற்றை பிரிவுகளாகக் கொண்டால், இவை ஒரு தொடர்ச்சியானத் தொடர் ஆகும். இங்கு 20 என்பது 20−30க்குள்ளும் 30 என்பது 30−40 க்குள்ளும் சேர்க்கப்பட வேண்டும். அதேபோல் மற்ற பிரிவுகளுக்கும் எண்ண வேண்டும்.

 (ஆ) கொடுக்கப்பட்டத் தொடரில் இரண்டு அடுத்தடுத்த பிரிவு எல்லைகளுக்கு இடையில் இடைவெளி இருப்பின் அந்த இடைவெளி அளவின் பாதியை இரண்டு எல்லைகளுக்கு இடையில் நிரப்பவேண்டும். இடைவெளி அளவின் பாதியை ஈடுசெய் காரணி என அழைக்கிறோம். 

தொடர்ச்சியற்றத் தொடரை, தொடர்ச்சியானத் தொடராக மாற்றுதல்:

கொடுக்கப்பட்டவை ஒரு தொடர்ச்சியற்ற தொடர் எனில், அதனை நாம் தொடர்ச்சியானதாகக் கீழ்க்கண்டவாறு மாற்றலாம். 

விளக்கம்: 1

மேல் வரம்பு = மேல் எல்லை + இடைவெளியின் பாதி

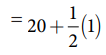= 20 + 0.5 

= 20.5

மேலும், இதேபோல் மற்ற பிரிவுகளுக்கும் செய்ய வேண்டும். 

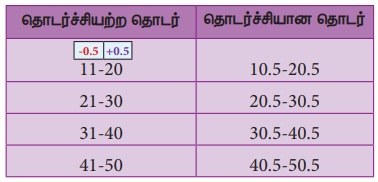
எனவே, பிரிவு இடைவெளித் தொடர்ச்சியானதாகக் கீழே அட்டவணையில் உள்ளது போல் மாற்ற முடியும்.

குறிப்பு

உள்ளடக்கியத் தொடர்:

பிரிவு இடைவெளிகளில், மேல் எல்லையும், கீழ் எல்லையும் அந்தப் பிரிவு இடைவெளியில் உள்ளடங்கி இருந்தால் அது உள்ளடக்கியத் தொடர் எனப்படும். 

எடுத்துக்காட்டாக: 11−20, 21−30, 31−40, 41−50 என்பது ஓர் உள்ளடக்கிய தொடர் ஆகும். இங்கு 11 மற்றும் 20 ஆகிய தரவுகள் (11−20) பிரிவு இடைவெளியினுள் அமையும். தெளிவாக இது ஒரு தொடர்ச்சியற்றத் தொடர் ஆகும். 

விலக்கியத் தொடர்: 

பிரிவு இடைவெளிகளில், ஒரு பிரிவு இடைவெளியின் மேல் எல்லையானது அடுத்த பிரிவு இடைவெளியின் கீழ் எல்லையாக இருந்தால் அது விலக்கியத் தொடர் ஆகும். 

எடுத்துக்காட்டாக: 10−15, 15−20, 20−25, 25−30, என்பன ஒரு விலக்கியத் தொடர் ஆகும். இங்கு 15 என்ற மதிப்பு 15−20 என்ற பிரிவு இடைவெளியிலும், 20 என்ற மதிப்பு அடுத்த 20−30 என்ற பிரிவு இடைவெளியிலும் இருக்கும். தெளிவாக இது ஒரு தொடர்ச்சியானத் தொடர் ஆகும். 

2. (i) தொகுக்கப்பட்ட நிகழ்வெண் பரவல் அட்டவணையை அமைத்தல்−தொடர்ச்சியானத் தொடர்

எடுத்துக்காட்டு 6.2

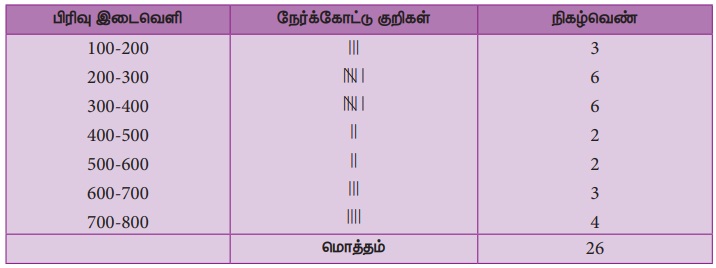
ஒரு கிராமத்திலுள்ள 26 வீடுகளின் மின்சாரக் கட்டணம் (₹ இல்) கீழேக் கொடுக்கப்பட்டுள்ளது. நிகழ்வெண் பரவல் அட்டவணையைத் தயார் செய்க.

தீர்வு :

அதிகபட்சக் கட்டணம் = ₹ 800 

குறைபட்சக் கட்டணம் = ₹ 120 

வீச்சு = அதிகபட்ச மதிப்பு – குறைந்தபட்ச மதிப்பு 

வீச்சு = 800 − 120 = ₹ 680

பிரிவின் அளவினை 100 என எடுக்க நினைத்தால்,

சாத்தியமான பிரிவு இடைவெளியின் எண்ணிக்கை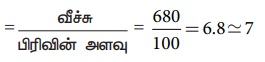

2. (ii) தொகுக்கப்பட்ட நிகழ்வெண் பரவல் அட்டவணையை அமைத்தல் – தொடர்ச்சியற்றத் தொடர்

எடுத்துக்காட்டு 6.3

கொடுக்கப்பட்ட தொடர்ச்சியற்ற தொடரை தொடர்ச்சியானத் தொடராக மாற்றுக. 

தீர்வு:

மேலே கூறியவாறு முதலில் நாம் இடைவெளியை நிரப்பவேண்டும். இடைவெளி அளவின் பாதியைக் கொண்டு இரண்டு அடுத்தடுத்த எல்லைகளுக்கு இடையிலுள்ள இடைவெளியை நிரப்பவேண்டும். இங்கு இடைவெளி அளவு 1 ஆகும். எனவே, இடைவெளி அளவின் பாதியை நீக்கவும், சேர்க்கவும் வேண்டும். அதாவது 0.5 ஐக் கீழ் எல்லையிலிருந்து கழித்தும், மேல் எல்லையுடன் கூட்டியும் ஒவ்வொரு பிரிவினையும் தொடர்ச்சியானதாக மாற்ற வேண்டும். 

இவற்றை முயல்க

கொடுக்கப்பட்ட விவரங்களுக்கு நிகழ்வெண் பரவல் அட்டவணையைத் தயார் செய்க. 

3, 4, 2, 4, 5, 6, 1, 3, 2, 1, 5, 3, 6, 2, 1, 3, 2, 4 

2. தொகுக்கப்பட்ட நிகழ்வெண் பட்டியலைத் தயார் செய்க. 

10, 9, 3, 29, 17, 34, 23, 20, 39, 42, 5, 12, 19, 47, 18, 19, 27, 7, 13, 40, 38, 24, 34, 15, 40