சார்புகள்

சார்புகள் (Functions)

ஆகாய வெளியில் ஒரு பொருள் நகர்கிறது எனவும், மேலும் அந்த பொருளை ஒரு புள்ளியாகவும் எடுத்துக்கொள்வோம். கால நேரத்தினைப் பொறுத்து பொருளின் நிலையும் மாறும். கணித முறையில், எந்த நேரத்திலும் ℝ3 என்ற முப்பரிமாண வெளியில் அப்புள்ளி ஒரு இடத்தினைப் பெறுகிறது. கால நேரத்தினை 0- லிருந்து 1 வரையிலான இடைவெளியாகக் கொள்வோம். இந்த இடைவெளியில் பொருளின் இடப்பெயர்வு அல்லது செயல்பாடானது பொருளின் நிலையினை முடிவு செய்கிறது. மாற்று மொழியில் கூறுவதாயின் ஒவ்வொரு t ∈ [0, 1] -க்கும் பொருளின் செயல்பாடானது ℝ3 -ல் ஒரு புள்ளியை தருகிறது. t எனும் எந்நேரத்திலும் பொருளின் நிலையினை f(t) எனக் குறிக்கலாம்.

இன்னொரு உதாரணமாக நேர்க்கோட்டினைக் குறிக்கும் சமன்பாடு 2x - y = 0 -ஐ எடுத்துக்கொள்வோம். இங்கு x எடுத்துக் கொள்ளும் ஒவ்வொரு மதிப்பிற்கும், y ஒரு மதிப்பினைப் பெறும். இங்கு y-ன் நகர்வு அல்லது செயல்பாடு x -ஐ பொறுத்து அமையும். இந்த y-ஐ f(x) எனக் குறிக்கலாம். இயற்கையில் இவ்வாறான நிகழ்வுகள் ஏராளமாக உள்ளன. இவற்றை ஆராயும் போது, ஒரு கணியத்தின் மாறுபாடு மற்றொரு கணியத்தினை சார்ந்திருப்பதை அறியலாம்.

நேரத்திற்கும் பொருளின் நிலைக்கும் உள்ள தொடர்பு, x - அச்சுத் தொலைவுக்கும் y - அச்சுத் தொலைவுக்கும் உள்ள தொடர்பு, மற்றும் இது போன்ற பல கருத்தாக்கங்கள் நூற்றாண்டுகளுக்கு முன்பே ‘சார்பு’ என்ற பெயரில் கையாளப்பட்டுள்ளது. கணிதவியலாளர் கேன்டர் என்பவருக்கு முன்னதாக, சார்பானது ஒரு மாறி இன்னொரு மாறியுடன் கொண்டுள்ள இசைவு விதியாகவே உணரப்பட்டது. அதற்குப் பின்னர் கணவியல் வளர்ச்சியின் காரணமாக சார்பு என்பது A என்ற கணத்தில் உள்ள ஒவ்வொரு உறுப்புக்கும் B என்ற கணத்தில் உள்ள ஒரு தனித்த உறுப்பினை இணைக்கும் விதியாக காணப்பட்டது. கணித ரீதியாக இசைவு மற்றும் விதி என்ற சொற்கள் முறையாக வரையறுக்கப்படவில்லை. தற்கால கணிதத்தில் ‘தொடர்பு’ மூலமாக சார்பின் வரையறையானது முறையாக வரையறுக்கப்படுகிறது.

இதனை ஒரு விளக்க எடுத்துக்காட்டுடன் காண்போம். ஒரு வகுப்பில் உள்ள மாணவர்கள் எழுதிய தேர்வினைப் பற்றி விவாதிப்பதாகக் கொள்வோம். இது ஒரு தொடர்பு என்பது புலப்படும்.

A என்பது தேர்வு எழுதிய மாணவர்களின் கணம் என்க. B = {0, 1, 2, 3, ..., 100} என்பது அவர்கள் பெறக்கூடிய சாத்தியமான மதிப்பெண்களின் கணம் என்க. தொடர்பு R -ஐ கீழ்க்கண்டவாறு வரையறுப்போம்.

தேர்வில் a என்ற மாணவன் b என்ற மதிப்பெண் பெற்றிருந்தால் மாணவர் a-ஐ மதிப்பெண் b யுடன் தொடர்புபடுத்தலாம்.

இந்த உதாரணத்திலிருந்து கீழ்க்காணும் கருத்துகள் பெறப்படுகிறது.

• ஒவ்வொரு மாணவரும் ஒரு மதிப்பெண்ணைப் பெற்றுள்ளனர். வேறுவிதமாகக் கூறினால் அனைத்து a ∈ A, (a, b) ∈ R எனுமாறு ஏதேனும் ஒரு உறுப்பு b ∈ B -ல் இருக்கும்.

• ஒரே தேர்வில் ஒரு மாணவர் இரண்டு வெவ்வேறு மதிப்பெண் பெற்றிருக்க முடியாது. வேறுவிதமாகக் கூறினால் ஒவ்வொரு a ∈ A, (a, b) ∈ R எனுமாறு உறுதியாக ஒரே ஒரு உறுப்பு b ∈ B -ல் இருக்கும். இன்னும் வேறுவிதமாகக் கூறினால் (a, b), (a, c) ∈ R எனில் b = c ஆகத்தான் இருக்க முடியும்.

மேற்கூறிய இரண்டு பண்புகளையும் கொண்டிருக்கும் தொடர்பானது ஒரு சார்பாக அமையும். இப்போது சார்புகளைப் பற்றிய முறையான வரையறையைக் காண்போம்.

அதாவது, சார்பகத்திலிருக்கும் ஒவ்வொரு உறுப்பும் வீச்சகத்திலுள்ள தனித்த ஒரு உறுப்புடன் கோர்க்கும் தொடர்புதான் சார்பாகும்.

f-ன் சார்பகம் (domain) A மற்றும் f -ன் துணைச்சார்பகம் (co-domain) B ஆகும். (a, b) ஆனது f-ல் இருந்தால் f(a) = b என எழுதுவோம். உறுப்பு b -ஐ a-ன் பிம்பம் (image) என்றும் a -ஐ b-ன் முன்பிம்பம் (pre-image) என்றும் கூறலாம். f (a) என்பது a-ல் f-ன் மதிப்பு ஆகும்.

{b : (a, b) ∈ f, ஏதோ சில a ∈ A} என்கிற கணத்தை சார்பின் வீச்சகம் (range) எனலாம். B ஆனது ℝ -ன் உட்கணமாக இருப்பின், அச்சார்பு மெய்மதிப்புடைச்சார்பு அல்லது மெய்மதிப்புச்சார்பு (real valued function) எனலாம்.

இரண்டு சார்புகள் f மற்றும் g சமம் (equal) எனில் அவற்றின் சார்பகங்கள் சமமாக இருந்து சார்பகத்திலுள்ள அனைத்து a -க்கும் f(a) = g(a) என இருத்தல் வேண்டும்.

f என்பது, சார்பகம் A மற்றும் துணைச்சார்பகம் B யைக் கொண்ட சார்பாக இருப்பின் அதனை f:A → B என எழுதலாம். (நிகழ்வுக்கு ஏற்றபடி இதனை f, A -லிருந்து B அல்லது f ஆனது A - லிருந்து B -க்குள்ள சார்பு எனப் படிக்கவும்.). மேலும் f ஆனது A -ஐ B உடன் கோர்த்தல் என்றும் கூறலாம். f(a) = b என்பதை f ஆனது a -ஐ b - க்கு இணைக்கிறது, a ஆனது b -ன் மேல் f ஆல் இணைக்கப்படுகிறது என்றும் கூறலாம்.

சார்பின் வீச்சகம் என்பது துணைச்சார்பகத்தில் முன்பிம்பத்தைப் பெற்றுள்ள அனைத்து உறுப்புகளின் கணமாகும். தெளிவாக, சார்பின் வீச்சகமானது துணைச்சார்பகத்தின் உட்கணமாகும். மேலும் சார்பின் முதல் நிபந்தனையானது சார்பகத்தில் உள்ள ஒவ்வொரு உறுப்பும் கண்டிப்பாக பிம்பத்தினைப் பெற்றிருக்க வேண்டும் என்று கூறுகிறது. இரண்டாம் நிபந்தனையானது சார்பகத்திலுள்ள உறுப்பானது இரண்டு அல்லது அதற்கும் மேற்பட்ட பிம்பங்களைப் பெற்றிருக்க கூடாது என்றும் கூறுகிறது. ஒரு தொடர்பின் சார்பகத்தை நாம் A என்று அழைக்கவில்லை என்பதனை கவனத்தில் கொள்ளவும். பிம்பங்கள் உள்ள A -ன் உறுப்புகளின் கணமே தொடர்பின் சார்பகமாகும். இயல்பாகவே, ஒருவருக்கு கீழ்க்காணும் ஐயங்கள் எழலாம்.

• ஆங்கில வரையறையில், பிம்பம் a -க்கு நிச்சயப் பெயர்க்குறியான "the" என்பதையும், b -ன் முன்பிம்பத்திற்கு நிச்சயமற்ற பெயர்க்குறியான "a" என்பதையும் ஏன் பயன்படுத்துகிறோம்? 

• சார்பகத்திலுள்ள ஒவ்வொரு உறுப்பும் கண்டிப்பாக பிம்பங்களைப் பெற்றிருக்க வேண்டும் என்று நிபந்தனையில் கூறப்பட்டுள்ளது. அதே போன்று துணைச்சார்பகத்தில் உள்ள ஒவ்வொரு உறுப்பும் முன்பிம்பங்களைப் பெற்றிருக்க வேண்டும் என்ற நிபந்தனை ஏதேனும் உண்டா ? இல்லையெனில் ஏன்?

• சார்பகத்திலுள்ள ஒவ்வொரு உறுப்புக்கும் இரண்டு அல்லது அதற்கு மேலான பிம்பங்கள் இருக்க இயலாது என்ற நிபந்தனையை அறிவோம். அதேபோன்று துணைச்சார்பகத்திலுள்ள ஒரு உறுப்புக்கு இரண்டு அல்லது அதற்கு மேலான முன்பிம்பங்கள் இருக்க இயலுமா? இல்லையெனில் காரணம் யாது?

சார்பகத்திலுள்ள ஒரு உறுப்புக்கு ஒரே ஒரு பிம்பம் மட்டுமே இருக்கும். ஆனால் வரையறையின்படி துணைச்சார்பகத்திலுள்ள ஒரு உறுப்புக்கு ஒன்றுக்கு மேலான முன்பிம்பங்கள் இருக்க இயலும். எனவே சார்பகத்திலுள்ள உறுப்புக்கு பிம்பத்தைப் பற்றிப் பேசும்போது நிச்சயமான "the" யும், முன்பிம்பங்களைப் பற்றி பேசும்போது நிச்சயமற்ற பெயர்க்குறி ‘a’ உம் பயன்படுத்தப் படுகிறது. கடைசி இரு வினாக்களுக்கு எந்தவித நிபந்தனைகளும் இல்லை. இதனை “மாணவர்கள் – மதிப்பெண்கள்” இடையேயான உதாரணம் மூலம் அறியலாம்.

எல்லா சார்பும் தொடர்பாகும் என்பது உண்மை என்றாலும் எல்லாத் தொடர்பும் சார்பாகும் என்று நம்மால் கூற இயலாது.

f = { (a, 1), (b , 2), (c, 2), (d, 4)} என எடுத்துக் கொள்வோம்.

f என்பது சார்பாக அமையுமா? கணம் {a, b, c, d} -லிருந்து கணம் {1, 2, 4} -க்கு இது சார்பாக அமையும். கணம் {a, b, c, d, e} - லிருந்து கணம் {1, 2, 3, 4} - க்கு இது சார்பாகாது. ஏனெனில் e என்ற உறுப்பு பிம்பத்தைப் பெற்றிருக்கவில்லை. கணம் {a, b, c, d} -லிருந்து கணம் {1, 2, 3, 5} -க்கு இது சார்பாகாது. ஏனெனில் d -ன் பிம்பம் துணைச்சார்பகத்தில் இல்லை. அதாவது f என்பது {a, b, c, d} × {1, 2, 3, 5} -ன் உட்கணமாக அமையவில்லை . எனவே எப்பொழுதெல்லாம் சார்புகளைக் கருதுகிறோமோ அப்பொழுதெல்லாம் சார்பகம் மற்றும் துணைச்சார்பகம் வெளிப்படையாகக் குறிப்பிடப்பட வேண்டும்.

விளக்க எடுத்துக்காட்டு 1.1 -ம் ஒரு சார்பு ஆகும். அதன் சார்பகம் { L, E, T, U, S, W, I, N } மற்றும் துணைச்சார்பகம் { O, H, W, X , V , Z, L, Q } ஆகும். மேலும் விளக்க எடுத்துக்காட்டு 1.3 கூட ஒரு சார்பாக அமையும். அதன் சார்பகம் {a, b, ..., z} மற்றும் துணைச்சார்பகம் {1, 2, 3, ..., 26}.

விளக்க எடுத்துக்காட்டு 1.2ல் மூன்று தொடர்புகள் உள்ளது. 

(i) y = 2x (ii) y = x2 (iii) y2 = x

தெளிவாக முதல் இரண்டும் சார்புகள் ஆகும். ஆனால் மூன்றாவது உதாரணத்தில் சார்பகமும் துணைச்சார்பகமும் ℝ எனும்போது சார்பு அல்ல. மூன்றாவது உதாரணத்தில் ஒரே x -க்கு, நமக்கு இரண்டு y மதிப்புகள் கிடைப்பது சார்பின் வரையறைக்கு முரணானது. ஆனால் இரண்டு தொடர்புகளாக அதாவது y = √x மற்றும் y = −√x எனப் பிரித்து எழுதும்போது இரண்டும், சார்பகங்களாக குறையற்ற மெய்யெண்களாகவும் துணைச்சார்பகங்களாக முறையே [0, ∞), (−∞, 0]  ஆகக் கொண்டு சார்புகளாக அமையும்.

1. சார்புகளை விவரிக்கும் வழிமுறைகள் (ways of representing functions)

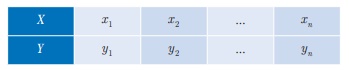
(a) அட்டவணை முறை (Tabular form)

சார்பகத்தின் உறுப்புகள் x1 , x2 , .... xn என வரிசைப்படுத்தும்போது அட்டவணை முறையைப் பயன்படுத்தலாம். சார்பக மதிப்புகளான x1 , x2 ,..., xn. மற்றும் அதற்குரிய சார்பின் மதிப்புகளான y1, y2, y3 . . . yn முதலியன திட்டவட்டமான வரிசையில் பின்வருமாறு அட்டவணையாக அமைக்கலாம்.

(b) வரைபட முறை (Graphical representation)

சார்பகம் மற்றும் துணைச்சார்பகம் ஆகியவை ℝ-ன் உட்கணங்களாக அமையும் போது, x - அச்சானது சார்பகத்தையும், y - அச்சானது துணைச்சார்பகத்தையும் xy - தளத்தில் குறிக்கும். விளக்க எடுத்துக்காட்டு 1.2 -ல் சார்புகளை f(x) = 2x, f(x) = x2 எனக் குறிக்கப்பட்டுள்ளதை நினைவு கூர்வோம். பொதுவாக, x ஆனது சாரா மாறியாகவும், y ஆனது சார்ந்த மாறியாகவும் செயல்படும். x என்பதனைக் கோணவீச்சம் அல்லது சார்பின் மாறி என்றும் f(x) -ஐ x-ல் சார்பு  f-ன் மதிப்பு என்றும் அழைக்கப்படுகிறது.

(c) பகுத்தாய்வு முறை (Analytical representation)

சார்பியல் தொடர்பு y = f (x) ஆகவும், f ஆனது ஒரு பகுப்பாய்வு கோவையை குறிப்பதாக இருப்பின், xஆல் உருவாக்கப்பட்ட சார்பு y -ஐ பகுப்பாய்வு முறையில் எழுதலாம்.

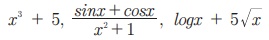போன்றவை சில பகுப்பாய்வு கோவைகளுக்கு உதாரணங்கள் ஆகும். அதாவது குறிப்பிட்ட கணிதச் செயல்பாடுகளை நிச்சயிக்கப்பட்ட வரிசையில், மாறிலிகள் அல்லது மாறிகளை மதிப்புகளாகக் கொண்ட எண்கள், எழுத்துகள் மூலம் குறிக்கும் ஒரு குறியீட்டுத் தொடராகும்.

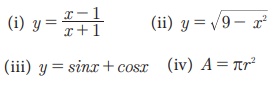
என்பவை பகுப்பாய்வு முறையில் வரையறுக்கப்பட்ட சில சார்புகள் ஆகும்.

பகுப்பாய்வு முறையில் எழுதும்போது இயற்கையாகச் சார்பகங்களை எளிமையாகக் கண்டுபிடித்து விடலாம். அதாவது, வலது புறத்தில் உள்ள பகுப்பாய்வுக் கோவையினைக் காணும் வகையில் அமைந்துள்ள x -ன் மதிப்புகளின் தொகுப்பு சார்பின் சார்பகமாகும்.

ஆகையால் சார்புகளின் இயல்பான சார்பகங்களில் சிலவற்றைக் காணலாம் 

இப்போது பகுப்பாய்வு முறையில் அமைந்துள்ள, ஏற்கனவே விவரிக்கப்பட்ட 

(i) y=2x

(ii) y = x2 

(iii) y = + √x

(iv) y = -√x

ஆகிய சார்புகளின் சார்பகங்களை நினைவு கூர்வோம்.

சிற்சமயங்களில் பகுதிவாரியாக வரையறுத்துள்ள சார்புகளை நாம் பயன்படுத்துவோம். உதாரணமாக, கீழ்வருமாறு வரையறுக்கப்பட்டுள்ள சார்பு  f: ℝ → ℝ ஆகக் கருதுக.

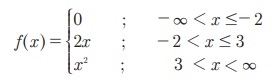
ஏதேனும் ஒரு புள்ளி x- க்கு f-ன்மதிப்பைக் காண, x-ன்மதிப்புகளைப் பொறுத்து, பொருத்தமான வரையறையைக் கையாள வேண்டும். ஏதேனும் ஒரு மெய்யெண்ணுக்கு f- ன் மதிப்பினைக் கணக்கிட, x ஆனது எந்த இடைவெளியில் உள்ளது என முதலில் கண்டறிய வேண்டும். பிறகு அதற்குரிய வரையறையைப் பயன்படுத்தி அப்புள்ளியில் f-ன் மதிப்பைக் காண வேண்டும். உதாரணமாக, f(6)-ன் மதிப்பைக் காண வேண்டுமாயின், இடைவெளி 3≤x<∞-ல் 6 அமைந்துள்ளதால் அதற்குரிய வரையறை f(x) = x2 -ஐ பயன்படுத்தி f(6) = 36 எனக் காணலாம். இதே போன்று f(-1) = -2, f(-5) = 0 என மதிப்புகளைக் காணலாம்.

சார்பானது ℝ-ன் உட்கணத்திலிருந்து அல்லது ℝ -லிருந்து வரையறுக்கப்பட்டால் சார்பின் வரைபடத்தை நம்மால் வரைய இயலும். உதாரணமாக f: [0, 4] → ℝ என்ற சார்பு f(x) = x/2 + 1 என வரையறுக்கப்படும்போது x ∈ [0,4] எனுமாறு (x, x/2 + 1) என்ற வடிவில் உள்ள புள்ளிகளைப் தளத்தில் குறிக்கலாம். இப்போது (0, 1) மற்றும் (4, 3) ஆகிய புள்ளிகளை இணைக்கும் நேர்க்கோட்டுத் துண்டினைப் பெறலாம். [படம் 1.13]

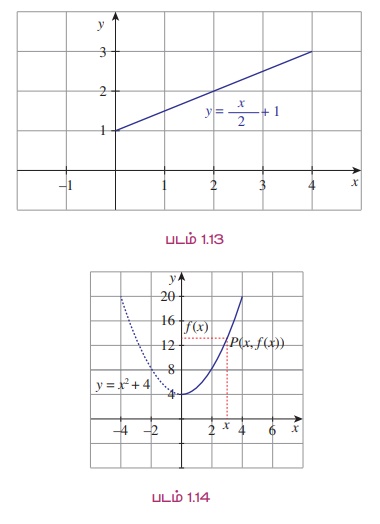
இன்னொரு உதாரணமாக, f (x) = x2 + 4x ≥ 0 என்ற சார்பினை எடுத்துக் கொள்வோம். இச்சார்பினை வரைபடம் மூலமாக படம் 1.14-ல் தரப்பட்டுள்ளது.

சார்பகத்தில் உள்ள ஒரு புள்ளி x என்க. புள்ளி x வழியாக ஒரு நிலைக்குத்துக்கோடு வரைவோம். அது வளைவரையை P என்ற புள்ளியில் சந்திக்கிறது என்போம். அப்புள்ளி P வழியாக ஒரு கிடைமட்டக் கோடு வரைந்தால் அது y அச்சில் சந்திக்கும் புள்ளி f (x) ஆகும். இதேப் போன்று துணைச்சார்பகத்தில் உள்ள புள்ளி y  வழியாகக் கிடைமட்டக் கோடு வரைந்தால் y -ன் முன்-பிம்பத்தை கண்டறியலாம்.

ℝ-ன் உட்கணத்திலிருந்து ℝ -க்கு ஒரு தளத்தின் மேல் வரையப்படும் எந்த ஒரு வளைவரையையும் சார்பு என்று சொல்ல முடியுமா? இல்லை, நம்மால் கூற இயலாது. அதைக் கண்டறிய ஓர் எளிதான சோதனை உள்ளது.

நிலைக்குத்துக் கோடு சோதனை (Vertical line test)

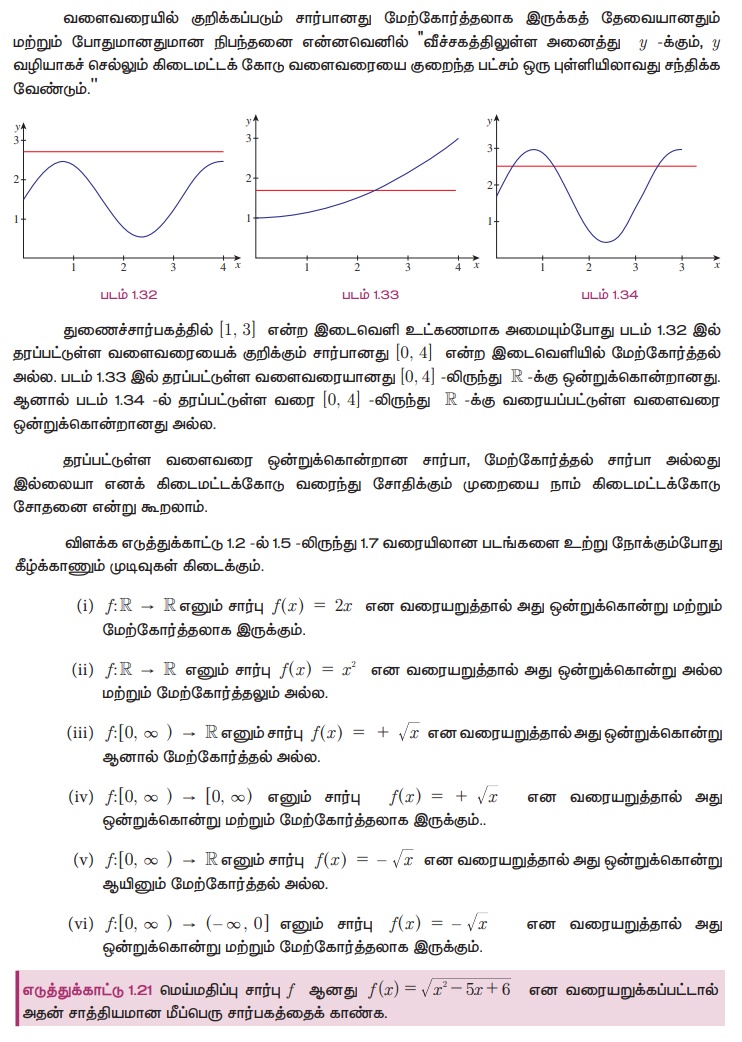
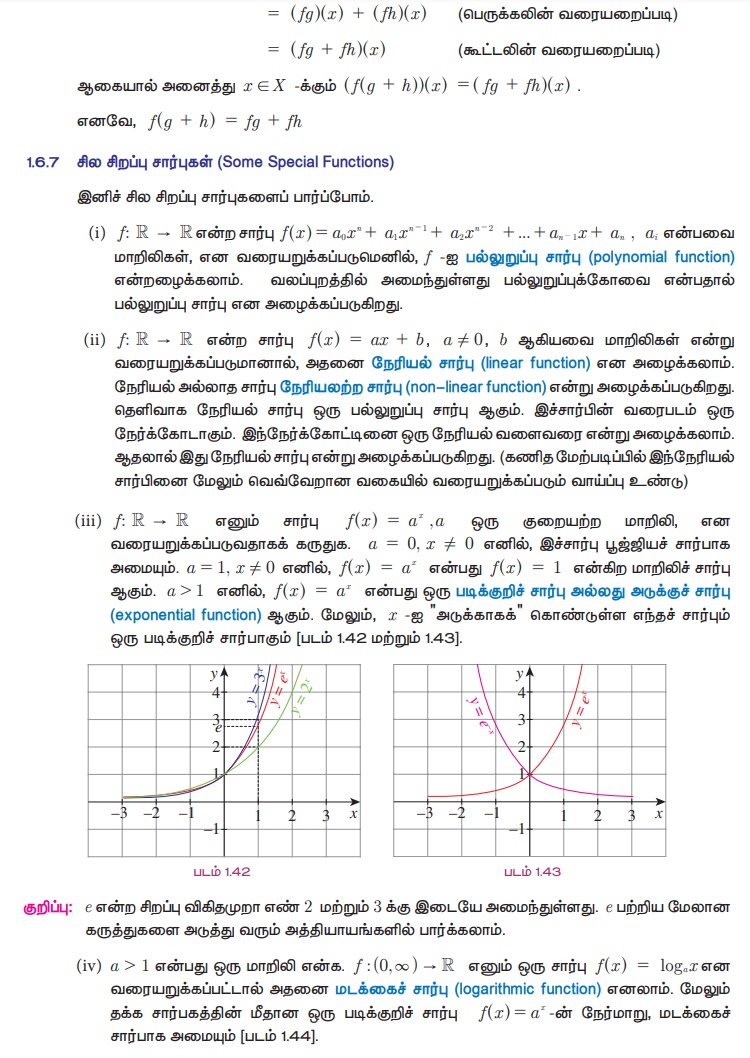
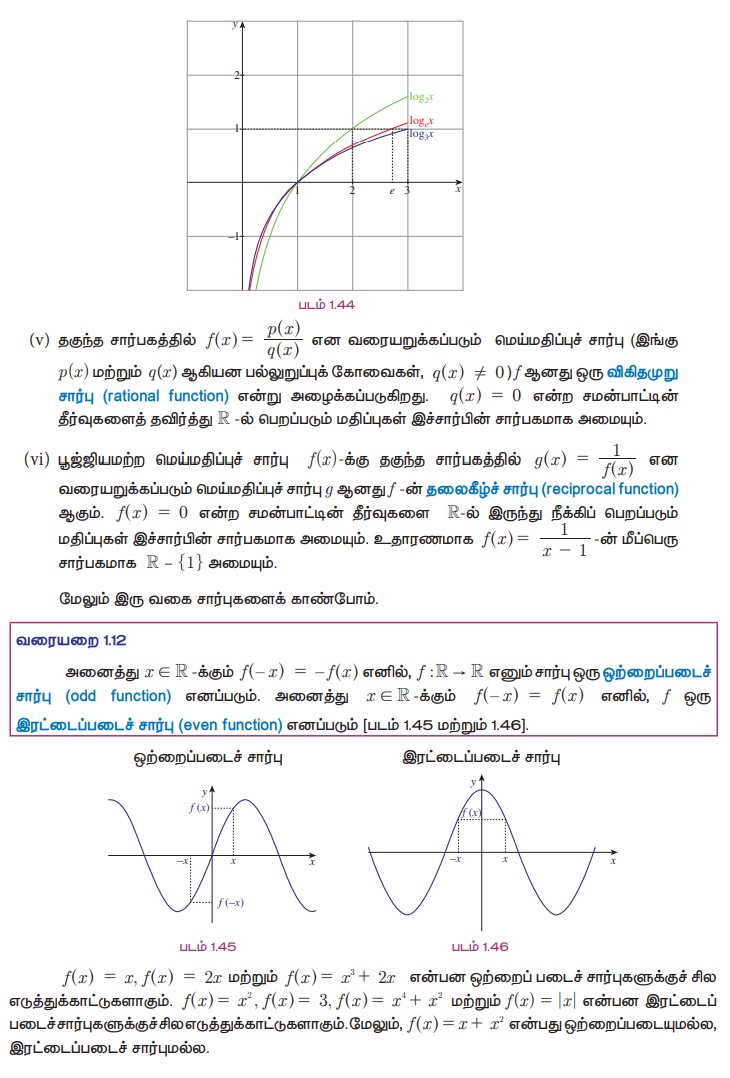
நாம் முன்னர் குறிப்பிட்டபடி, சார்பகத்தில் உள்ள ஏதேனும் ஒரு புள்ளி x வழியாகச் செல்லும் ஒரு நிலைக்குத்துக் கோடு, வளைவரையைச் சில புள்ளிகளில் சந்திக்கலாம். அப்போது y-ன் ஆயத்தொலை f (x) ஆகும். சார்பகத்தில் உள்ள புள்ளி x வழியாகச் செல்லும் நிலைக்குத்துக்கோடு வளைவரையை ஒன்றுக்கும் மேற்பட்ட புள்ளிகளில் சந்தித்தால், ஒரு x க்கு பல f(x) மதிப்புகளை நாம் பெறலாம். ஆனால் இவ்வாறு சார்பில் அனுமதிக்கப்படுவதில்லை. மேலும், சார்பகத்திலுள்ள புள்ளி வழியாகச் செல்லும் நிலைக்குத்துக் கோடு வளைவரையைச் சந்திக்கவில்லை எனில் x- க்கு எந்த பிம்பமும் அங்கு இருக்காது. இதுவும் சார்பில் சாத்தியம் இல்லை. எனவே,

"சார்பகத்தில் உள்ள புள்ளி x வழியாகச் செல்லும் நேர்குத்துக்கோடு வளைவரையை ஒரு புள்ளிக்கு மேல் சந்தித்தாலோ அல்லது சந்திக்காமலிருந்தாலோ அப்பொழுது அவ்வளைவரை சார்பைக் குறிக்காது என்று நாம் கூறலாம்."

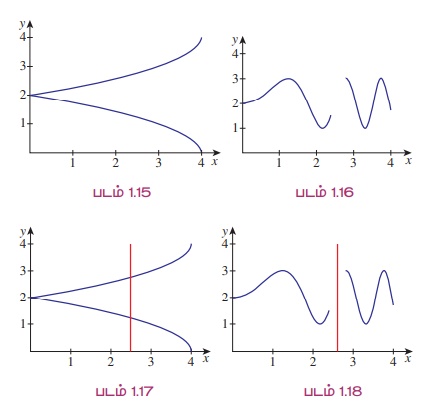
படம் 1.15 -ல் [0, 4] -லிருந்து ℝ -க்கு வரையப்பட்டுள்ள வளைவரையானது சார்பாகாது. ஏனெனில் படம் 1.17-ன் படி நிலைக்குத்துக்கோடு வளைவரையை ஒரு புள்ளிக்கு மேல் சந்திக்கிறது. படம் 1.16-ல் காட்டப்பட்டுள்ள வளைவரையும் (0, 4) - லிருந்து ℝ-க்கு சார்பாகாது. ஏனெனில் படம் 1.18 -ன் படி x = 2.5-ல் வரையப்படும் நிலைக்குத்துக்கோடு வளைவரையை எங்கும் சந்திக்கவில்லை.

தரப்பட்டுள்ள வளைவரை ஒரு சார்பா? இல்லையா? என நிலைகுத்துக்கோடு வரைந்து கண்டறியும் முறையை நிலைக்குத்துக் கோடு சோதனை என்று கூறலாம்.

விளக்க எடுத்துக்காட்டு 1.2 -ல் உள்ள மூன்றாவது வளைவரை y2=x ஆனது நிலைக்குத்துக்கோடு சோதனை மூலம் ℝ → ℝ-ல் அது சார்பு இல்லை எனப் புரிந்து கொள்ளலாம்.

2. சில எளிமையான சார்புகள் (Some elementary functions)

அடிக்கடி பயன்படுத்தும் சில சார்புகளை அதன் பெயர்கள் மூலம் அறியலாம். சிலவற்றை இங்குப் பட்டியலிடுவோம்.

(i) ஏதேனும் ஒரு வெற்றற்ற கணம் X என்க.  சார்பானது f(x) → x என்ற சார்பானது f (x)  = x என அனைத்து x ∈ X - க்கும் வரையறுக்கப்பட்டால் அதனை X - ன் மீதான சமனிச் சார்பு (identity function) என்று அழைக்கலாம். மேலும் அதனை Ix எனவும் குறிப்பிடலாம். [படம் 1.19]

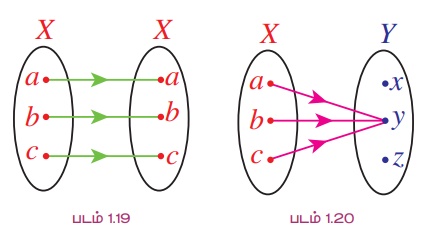
(ii) X மற்றும் Y என்பவை இரு கணங்கள். மேலும் Y -ல் உள்ள ஒரு நிலையான உறுப்பு c என்க. f : X → Y என்ற சார்பானது f(x) = c என அனைத்து x ∈ X -க்கும் வரையறுக்கப்பட்டால் அதனை மாறிலிச் சார்பு (constant function) என்று கூறலாம். மாறிலிச் சார்பின் மதிப்புகள் சார்பகம் முழுமைக்கும் ஒரே மதிப்பாகும் [படம் 1.20].

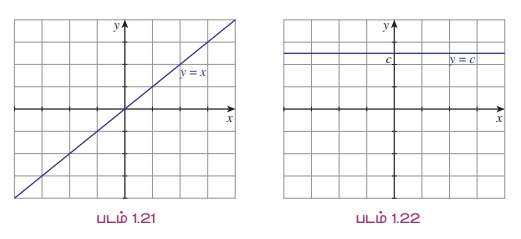
இங்கு X மற்றும் Y ஆகிய கணங்கள் ℝ ஆக இருப்பின் சமனிச்சார்பு மற்றும் மாறிலிச் சார்பின் வரைபடங்கள் முறையே படம் 1.21 மற்றும் 1.22 ஆக அமையும்

ஏதேனும் ஒருகணம் X என்க. அனைத்து x ∈ X - க்கும் f (x) = 0 என வரையறுக்கப்பட்டால் அதனை பூஜ்ஜிய சார்பு (zero function) என்று அழைக்கப்படும்.

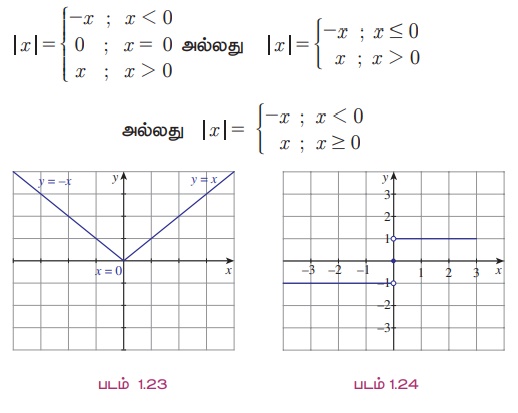
(iii) f : ℝ → ℝ என்ற சார்பு f(x) = |x| என வரையறுக்கப்பட்டால் (இங்கு |x| என்பது x ன் மட்டு அல்லது எண்ணளவு மதிப்பாகும்) அதனை மட்டுச் சார்பு அல்லது எண்ணளவு சார்பு (modulus or absolute value function) எனக் கூறலாம் [படம் 1.23]. |x| என்பது கீழ்க்காணுமாறு வரையறுக்கப்படுகிறது.

(iv) f : ℝ → ℝ என்ற சார்பானது

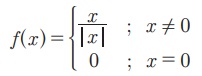என வரையறுக்கப்பட்டால், இச்சார்பினை குறியீட்டுச்சார்பு (signum function) எனலாம். இச்சார்பினை sgn சார்பு எனவும் குறிப்பிடலாம் [படம் 1.24].

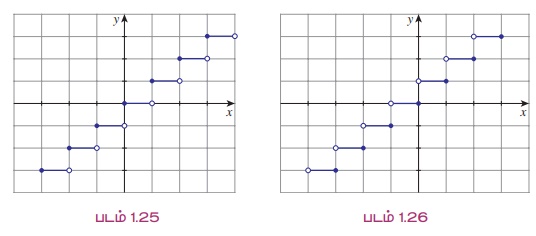
(v) f: ℝ → ℝ என்ற சார்பில் f(x) என்பது, x -ஐ விடக் குறைவாகவோ அல்லது சமமாகவோ இருக்கும் மீப்பெரு முழு எண் என வரையறுக்கப்பட்டால் அச்சார்பு மீப்பெரு முழு எண் சார்பு (greatest integer function) அல்லது floor சார்பு என அழைக்கப்படும். இச்சார்பினை எனக் குறிப்பிடலாம் [படம் 1.25]

(vi) f: ℝ    ℝ என்ற சார்பில் f(x) என்பது, x -ஐ விட அதிகமாகவோ அல்லது சமமாகவோ இருக்கும் மீச்சிறு முழு எண் என வரையறுக்கப் பட்டால் அச்சார்பு மீச்சிறு முழு எண் சார்பு (smallest integer function) அல்லது ceil சார்பு எனப்படும். இச்சார்புக்கான குறியீடு ஆகும். அதாவது இச்சார்பினை எனக் குறிப்பிடலாம் [படம் 1.26]. மேற்குறிப்பிட்ட இரு சார்புகளையும் படிநிலைச் சார்புகள் (step functions) எனவும் அழைக்கலாம். பின்வருவனவற்றைக் கவனிக்கவும்.

இந்தச் சார்புகளின் பெயர்களுக்கும் சார்புகளைக் குறிக்கின்ற குறியீடுகளுக்கும் இடையே உள்ள தொடர்பானது நாம் பொதுவாக அறைக்குப் பயன்படும் மேற்கூரை மற்றும் தரையைக் குறிக்கும் வார்த்தைகளாகும் என்பதைக் கவனிக்கவும்.

3. சார்புகளின் வகைகள் (types of functions)

சார்புகளை, அதன் தேவையினைப் பொறுத்துப் பல வகைகளாகப் பிரிக்கப்பட்டிருந்தாலும், நாம் இரண்டு அடிப்படை வகைகளில் கவனம் செலுத்தப் போகிறோம். அவை ஒன்றுக்கொன்றான சார்பு மற்றும் மேற்கோர்த்தல் சார்பு ஆகும்.

படம் 1.27 மற்றும் படம் 1.28 ஆகியவற்றில் தரப்பட்டுள்ள இரண்டு எளிய சார்புகளைப் பார்ப்போம். முதல் சார்பில் சார்பகத்தில் உள்ள இரண்டு உறுப்புகள் b,c ஆகியவை y என்ற ஒரே உறுப்புடன் கோர்க்கப்பட்டுள்ளது. அதே சமயம் படம் 1.28 - ல் அவ்வாறு கோர்க்கப்படவில்லை. இரண்டாவது வகையாக படம் 1.28 - ல் குறிப்பிட்டுள்ள மாதிரியான சார்புகள் ஒன்றுக்கொன்றான சார்புகளுக்கு உதாரணங்களாகும்.

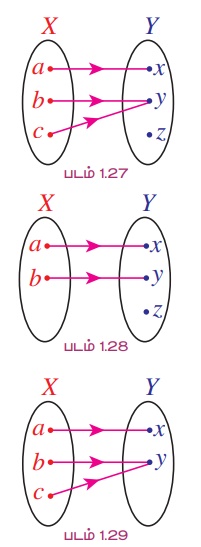
தற்போது, படங்கள் 1.28 மற்றும் 1.29 ஆகியவற்றை உற்றுநோக்குவோம். படம் 1.28 -ல் z என்ற உறுப்புக்கு முன்பிம்பம் இல்லை. ஆனால் படம் 1.29 -ல் அவ்வாறு முன்பிம்பம் இல்லாத உறுப்புகள் இல்லை. படம் 1.29 -ல் குறிப்பிட்டுள்ள மாதிரியான சார்பு மேற்கோர்த்தல் சார்புக்கு உதாரணமாகும். இப்போது ஒன்றுக்கொன்றான மற்றும் மேற்கோர்த்தல் சார்புகளை வரையறுப்போம்.

வரையறை 1.7

f:A→B என்ற சார்பு, ஒன்றுக்கொன்றான சார்பாக (one-to-one function) இருக்க வேண்டுமாயின், x,y ∈ A, x ≠ y ⇒ f(x) ≠ f(y) எனுமாறு [அல்லது நிகராக f(x) = f(y) ⇒ x = y] அமைய வேண்டும். f: A → B என்ற சார்பு, மேற்கோர்த்தல் சார்பாக (onto function) இருக்க வேண்டுமாயின், ஒவ்வொரு b ∈ B -க்கும், f(a) = b எனுமாறு குறைந்தபட்சம் ஒரு உறுப்பு a ∈ A என இருக்கவேண்டும். அதாவது f-ன் வீச்சகம் B ஆக இருத்தல் வேண்டும்.

ஒன்றுக்கொன்றான சார்பினை உள் செலுத்தும் சார்பு (injective) என்றும், மேற்கோர்த்தல் சார்பினை மேல் செலுத்தும் சார்பு (surjective) என்றும் அழைக்கலாம். மேலும் ஒன்றுக்கொன்று மற்றும் மேற்கோர்த்தல் என இரண்டையும் பெற்றிருந்தால் அச்சார்பை இருபுறச் சார்பு (bijective) என்று கூறலாம்.

f: A → B என்ற சார்பு ஒன்றுக்கொன்றானது என நிரூபிக்கக் கீழ்க்காணும் ஏதேனும் ஒன்றினை நிரூபித்தால் போதுமானது.

• x ≠ y எனில் f(x) ≠ f(y) அல்லது 

• f(x) = f(y) எனில் x = y.

ஒவ்வொரு சமனிச்சார்பும் ஒன்றுக்கொன்று மற்றும் மேற்கோர்த்தல் சார்பு என்று எளிதாக அறிய முடியும். மாறிலிச் சார்பில் துணைச்சார்பகம் ஒரே ஒரு உறுப்பினைப் பெற்றில்லாதவரை அது மேற்கோர்த்தல் சார்பு ஆகாது.

கீழ்வருவன சில முக்கியமான எளிய முடிவுகளாகும்.

A மற்றும் B ஆகியவை m மற்றும் n உறுப்புகள் கொண்ட இரு கணங்கள் என்க. 

(i) m > n எனில் A -லிருந்து B -க்கு ஒன்றுக்கொன்று சார்பு கிடையாது. 

(ii) A - லிருந்து B -க்கு ஒன்றுக்கொன்று சார்பு இருந்தால் அப்போது m ≤ n

(iii) m < n எனில் A -லிருந்து B -க்கு மேற்கோர்த்தல் சார்பு கிடையாது. 

(iv) A - லிருந்து B - க்கு மேற்கோர்த்தல் சார்பு இருந்தால் m ≥ n. 

(v) A -லிருந்து B -க்கு இருபுறச் சார்பாக இருக்கத் தேவையானதும் போதுமானதுமான நிபந்தனை m = n ஆகும். 

(vi) A -லிருந்து B -க்கு இருபுறச் சார்பாக இல்லாமல் இருக்கத் தேவையானதும் போதுமானதுமான நிபந்தனை m ≠ n ஆகும்.

குறிப்பு: ஒரு சார்பு மேற்கோர்த்தல் இல்லையெனில் அதனை உள் சார்பு (into) என அழைக்கலாம். அதாவது ஒரு சார்பு மேற்கோர்த்தல் இல்லையெனில் வீச்சகமானது துணைச்சார்பகத்தின் தகு உட்கணமாக அமையும்.

சில விளக்க எடுத்துக்காட்டுக்களை இப்பொழுது பார்ப்போம்.

(i) X = {1, 2, 3, 4}, Y = {a, b, c, d, e} மற்றும் f = {(1, a), (2, c), (3, e), (4, b)}

இச்சார்பு ஒன்றுக்கொன்றான சார்பு ஆனால் மேற்கோர்த்தல் அல்ல.

(ii) X = {1, 2, 3, 4}, Y = {a, b} மற்றும் f = {(1, a), (2, a), (3, a), (4, a)}.

இச்சார்பு ஒன்றுக்கொன்று அல்ல. மேலும் மேற்கோர்த்தலும் அல்ல.

(iii) X = {1, 2, 3, 4}, Y = {a} மற்றும் f = {(1, a), (2, a), (3, a), (4, a)}.

இச்சார்பு ஒன்றுக்கொன்று அல்ல. ஆனால் மேற்கோர்த்தல் சார்பாகும். இது எடுத்துக்காட்டு (ii) போலவே உள்ளது. ஆனால் துணைச்சார்பகம் மாறியுள்ளது. எனவே சார்பானது மேற்கோர்த்தலா? இல்லையா என்பதனைத் தீர்மானிப்பதற்கு, சார்பின் துணைச்சார்பகம் மிகவும் முக்கியமானதாகும். 

(iv) X = {1, 2, 3, 4}, Y = {a, b, c, d, e} மற்றும் f = {(1, a), (2, c), (3, b), (4, b)}.

இந்தச் சார்பு ஒன்றுக்கொன்றும் இல்லை, மேற்கோர்த்தலும் இல்லை.

(v) X = {1, 2, 3, 4}, Y = {a, b, c, d } மற்றும் f = {(1, a), (2, c), (3, d), (4, b)}

இந்தச் சார்பு ஒன்றுக்கொன்று மற்றும் மேற்கோர்த்தலும் ஆகும்.

(vi) X = {1, 2, 3, 4}, Y = {a, b, c, d, e} மற்றும் f = {(1, a), (2, c), (3, e) }

இது சார்பே அல்ல. இது வெறும் தொடர்பு மட்டுமே ஆகும்.

(vii) X என்பது k உறுப்புகள் உள்ள முடிவுறு கணம் என்க. இப்போது X -லிருந்து {1,2,3,..., k} என்ற கணத்திற்கு இருபுறச் சார்பு உருவாக்கலாம்.

தெரிந்த கணங்களின் மீது, விதிகள் வழியாக வரையறுக்கப்படும் சில சார்புகளைக் காணலாம்.

எடுத்துக்காட்டு 1.14 கீழ்க்காணும் சார்புகள் ஒன்றுக்கொன்று மற்றும் மேற்கோர்த்தல் சார்புகளா எனச் சரிபார்க்கவும்.

(i) f: ℕ → ℕ எனும் சார்பு f (n) = n + 2 என வரையறுக்கப்படுகிறது.

(ii) f: ℕ U {-1, 0} → ℕ எனும் சார்பு f(n) = n + 2 என வரையறுக்கப்படுகிறது.

தீர்வு :

(i) f(n) = f(m) என எடுத்துக்கொண்டால் n + 2 = m + 2. இதிலிருந்து m = n. இதனால் f ஆனது ஒன்றுக்கொன்று ஆகும். 1 என்ற உறுப்பிற்கு முன்பிம்பம் இல்லை என்பதால் இச்சார்பு மேற்கோர்த்தல் அல்ல (படம் 1.30].

(ii) மேற்கண்டவாறு இச்சார்பு ஒன்றுக்கொன்றாகும். துணைச்சார்பகத்தில் m இருந்தால் m - 2 என்பது சார்பகத்தில் இருக்கும். மேலும் f(m - 2) = (m - 2) + 2 = m. இதனால் துணைச்சார்பகத்திலுள்ள m என்ற உறுப்பு முன்பிம்பத்தைக் கொண்டுள்ளது. எனவே இச்சார்பு மேற்கோர்த்தல் ஆகும் [படம் 1.31].

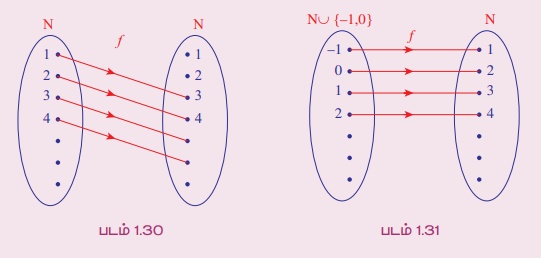
குறிப்பு: இரண்டாவதாக குறிப்பிட்டுள்ள சார்பு முதலில் உள்ள சார்பு போலவே தோன்றும். ஆனால் சார்பகங்கள் வெவ்வேறாகும். இதிலிருந்து சார்பானது மேற்கோர்த்தலா, இல்லையா என்பதனைத் தீர்மானிப்பதற்கு, சார்பின் சார்பகம் முக்கியம் எனத் தெரிந்து கொள்ளலாம். ஒரு சார்பு ஒன்றுக்கொன்று என்பதனை துணைச்சார்பகம் தீர்மானிப்பதில்லை. ஆனால் துணைச்சார்பகம் மேற்கோர்த்தலை தீர்மானிக்கிறது.

தற்போது விளக்க எடுத்துக்காட்டு 1.1 -ல்

C = { L, E, T ,U, S, W, I, N } மற்றும் D = { O, H, W, X ,V, Z, L, Q} மற்றும்

f(L) = O, f (E) = H, f (T) = W, f (U) = X, f (S) = V, f(W) = Z, f(I) = L, f(N) = Q 

என வரையறுக்கப்பட்ட சார்பு f:C→D, ஒன்றுக்கொன்று மற்றும் மேற்கோர்த்தலுமாகும்.

ஆனால் விளக்க எடுத்துக்காட்டு 1.3 -ல் f(a) = 1, f(b) = 2, f(c) = 3, f(z) = 26 என வரையறுக்கப்பட்ட சார்பு f:A→ℕ, ஒன்றுக்கொன்று ஆனால் மேற்கோர்த்தல் அல்ல. ℕ -க்கு பதிலாக {1,2,3,..., 26} என எடுத்துக்கொண்டால் ஒன்றுக்கொன்று மற்றும் மேற்கோர்த்தலும் ஆகும். 

குறிப்பு: ℝ-{0} என்பதைத் துணைச்சார்பகமாக இரண்டாவது உதாரணத்திற்கு எடுத்துக் கொண்டால் இது இருபுறச் சார்பு ஆகும்.

குறிப்பு: f(x) = 2x3 என்ற சார்பு [-2, 2] என்ற இடைவெளியில் ஏறும் சார்பாக இருப்பதால் இடைவெளியின் இடப்பக்க மதிப்பில் சார்பின் மீச்சிறு மதிப்பினையும் வலப்பக்க மதிப்பில் சார்பில் மீப்பெரு மதிப்பினையும் பெறும் [ஏறும்/இறங்கும் சார்பினைப் பற்றி பின்னர் வரும் பகுதிகள் மூலம் தெரிந்து கொள்ளலாம்.]

குறிப்பு: f (x) = x| x | என்ற சார்பு ஏறும் சார்பாகும்.

கிடைமட்டக்கோட்டு சோதனை (Horizontal test)

நிலைக்குத்துக்கோடு சோதனையைப் போலவே உள்ள ஒரு சோதனை கிடைமட்டக்கோடு சோதனையாகும். இதன் மூலம் சார்பானது ஒன்றுக்கொன்றா, மேற்கோர்த்தலா எனச் சரிபார்க்கலாம். தளத்தில் உள்ள வளைவரையாகச் சார்பு தரப்பட்டுள்ளது என்க. துணைச்சார்பகத்தில் உள்ள ஒரு புள்ளி y வழியாக வரையப்படும் கிடைமட்டக்கோடு வளைவரையில் சில புள்ளிகளில் சந்திக்கும். அப்பொழுது கிடைக்கும் ஆயத்தொலை புள்ளிகள் அனைத்தும் y -ன் முன்பிம்பங்களை கொடுக்கும்.