Я«цЯ«┐Я«Ъ Я«еЯ«┐Я«▓Я»ѕЯ««Я»ѕ | Я«хЯ»ЄЯ«цЯ«┐Я«»Я«┐Я«»Я«▓Я»Ї - Я«фЯ«ЪЯ«┐Я«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«фЯ»іЯ«цЯ«┐Я«хЯ»Ђ | 12th Chemistry : UNIT 6 : Solid State
12 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«хЯ»ЄЯ«цЯ«┐Я«»Я«┐Я«»Я«▓Я»Ї : Я«ЁЯ«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«»Я««Я»Ї 6 : Я«цЯ«┐Я«Ъ Я«еЯ«┐Я«▓Я»ѕЯ««Я»ѕ
Я«фЯ«ЪЯ«┐Я«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«фЯ»іЯ«цЯ«┐Я«хЯ»Ђ
Я«фЯ«ЪЯ«┐Я«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«фЯ»іЯ«цЯ«┐Я«хЯ»Ђ
Я«фЯ«┤Я«ЋЯ»ЇЯ«ЋЯ«ЪЯ»ѕЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«фЯ«┤Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»ѕ Я«еЯ«ЙЯ««Я»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЂЯ«хЯ»ІЯ««Я»Ї. Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«ЁЯ«хЯ»ѕЯ«ЋЯ«│Я»Ї Я«еЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«Е. Я«еЯ«ЙЯ««Я»Ї Я«ЄЯ«еЯ»ЇЯ«ц Я«њЯ«фЯ»ЇЯ«фЯ»ЂЯ««Я»ѕЯ«»Я«┐Я«ЕЯ»ѕ, Я«фЯ«ЪЯ«┐Я«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«ЅЯ«ЪЯ»ЇЯ«ЋЯ»ѓЯ«▒Я»ЂЯ«ЋЯ«│Я»ѕ (Я«ЁЯ«БЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»Ї, Я««Я»ѓЯ«▓Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«▒Я»ЂЯ«ЋЯ«│Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«ЁЯ«»Я«ЕЯ«┐Я«ЋЯ«│Я»Ї ) Я«цЯ«┐Я«Ъ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«ЁЯ«хЯ»ѕЯ«ЋЯ«│Я»Ї Я«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«цЯ»Ђ Я«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«џЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«фЯ»Ї Я«фЯ»ЂЯ«░Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«│Я«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«▓Я«ЙЯ««Я»Ї. Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Ћ Я«фЯ«ЪЯ«┐Я«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї, Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«ЅЯ«ЪЯ»ЇЯ«ЋЯ»ѓЯ«▒Я»ЂЯ«ЋЯ«│Я»Ї, Я«цЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ѕЯ«»Я»ЄЯ«»Я«ЙЯ«Е Я«ЋЯ«хЯ«░Я»ЇЯ«џЯ»ЇЯ«џЯ«┐ Я«хЯ«┐Я«џЯ»ѕЯ«»Я«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ««Я««Я«ЙЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ«хЯ»ѕЯ«ЋЯ«│Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я«┐Я«▒Я»ЇЯ«ЋЯ»іЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«јЯ«хЯ»ЇЯ«хЯ«│Я«хЯ»Ђ Я«ЁЯ«░Я»ЂЯ«ЋЯ«ЙЯ««Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ«ЙЯ«»Я»ЇЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»І Я«ЁЯ«еЯ»ЇЯ«ц Я«ЁЯ«│Я«хЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«фЯ»Ї Я«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я««Я»ЂЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е.

Я«ЄЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«њЯ«░Я»Є Я««Я«ЙЯ«цЯ«┐Я«░Я«┐Я«»Я«ЙЯ«Е Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«▒Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«фЯ»ЇЯ«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«ц Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»ѕ Я«јЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«▒Я»ЇЯ«▒Я«▒Я«┐Я«хЯ»ІЯ««Я»Ї. Я«фЯ«ЙЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕ Я«еЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«фЯ»ЂЯ«░Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ««Я»Ї Я«фЯ»іЯ«░Я»ЂЯ«ЪЯ»ЇЯ«ЪЯ»Ђ, Я««Я»ЂЯ«фЯ»ЇЯ«фЯ«░Я«┐Я««Я«ЙЯ«Б Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«фЯ»Ї Я«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«фЯ«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«ЕЯ»ЇЯ«ЕЯ«░Я»Ї, Я««Я»ЂЯ«цЯ«▓Я«┐Я«▓Я»Ї Я«ЄЯ«░Я»Ђ Я«фЯ«░Я«┐Я««Я«ЙЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«јЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«▒Я»ЇЯ«фЯ»ІЯ««Я»Ї.
1. Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«цЯ«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ«▓Я»Ї
Я«њЯ«░Я»Ђ Я«фЯ«░Я«┐Я««Я«ЙЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«цЯ«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї, Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«њЯ«░Я»Є Я«њЯ«░Я»Ђ Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Є Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЋЯ»ІЯ«│Я««Я»ЂЯ««Я»Ї Я«цЯ«ЕЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«░Я»ЂЯ«ЋЯ«ЙЯ««Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«фЯ»ЂЯ«▒Я««Я»ЂЯ««Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«ЄЯ«░Я»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
2. Я«ЄЯ«░Я»ЂЯ«фЯ«░Я«┐Я««Я«ЙЯ«Б Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«фЯ»Ї Я«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ
Я«ЄЯ«░Я»Ђ Я«фЯ«░Я«┐Я««Я«ЙЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«цЯ«│Я«ЁЯ««Я»ѕЯ«хЯ«┐Я«▓Я»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«ЈЯ«цЯ»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«фЯ»Ї Я«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕ Я«еЯ«ЙЯ««Я»Ї Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«Ћ Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї.
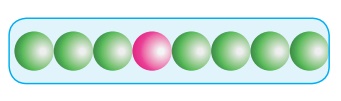
(i) AAA... Я«хЯ«ЋЯ»ѕ
Я«њЯ«░Я»Ђ Я«цЯ«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«цЯ»ѕЯ«фЯ»Ї Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЄЯ«░Я»Ђ Я«фЯ«░Я«┐Я««Я«ЙЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЁЯ«цЯ»Є Я«хЯ«░Я«┐Я«џЯ»ѕ Я««Я»ђЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я««Я»ђЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«цЯ»ІЯ«ЕЯ»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ«▓Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я«хЯ«ЙЯ«▒Я»Ђ, Я«њЯ«░Я»Ђ Я«фЯ«░Я«┐Я««Я«ЙЯ«Б Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ, Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ««Я«ЪЯ»ЇЯ«Ъ Я«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Є Я«цЯ«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«фЯ«▓ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«ЋЯ«│Я»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ«▓Я»Ї Я««Я»ЂЯ«цЯ«▓Я«ЙЯ«хЯ«цЯ»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«ЕЯ»ѕ Я«еЯ«ЙЯ««Я»Ї A Я«јЯ«Е Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї, Я«фЯ«┐Я«ЕЯ»Ї Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«цЯ»Ђ Я«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЕЯ«цЯ»Ђ AAA Я«хЯ«ЋЯ»ѕ Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«ЈЯ«ЕЯ»єЯ«ЕЯ«┐Я«▓Я»Ї Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«ЋЯ«│Я»ЂЯ««Я»Ї, Я««Я»ЂЯ«цЯ«▓Я»Ї Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«ЕЯ»ѕ Я«њЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЁЯ««Я»ѕЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«ЄЯ«хЯ»ЇЯ«хЯ«ЋЯ»ѕ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї, Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЋЯ»ІЯ«│Я««Я»ЂЯ««Я»Ї Я«цЯ«ЕЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«░Я»ЂЯ«ЋЯ«ЙЯ««Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«џЯ»ѓЯ«┤Я»ЇЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
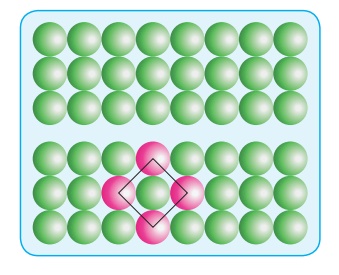
(i) ABAB... Я«хЯ«ЋЯ»ѕ
Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ, Я«ЄЯ««Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЪЯ»ЂЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ђЯ«┤Я»Ї Я«ЋЯ«ЙЯ«БЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«хЯ»єЯ«│Я«┐Я«фЯ»Ї Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«фЯ»іЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я««Я»ЂЯ«цЯ«▓Я»Ї Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«ЕЯ»ѕ A Я«хЯ«░Я«┐Я«џЯ»ѕ Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї, Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«ЕЯ»ѕ B Я«хЯ«░Я«┐Я«џЯ»ѕ Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї, Я«ЄЯ««Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«хЯ«цЯ»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕ Я««Я»ђЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї A Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»ЂЯ««Я»Ї, Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ«ЙЯ«хЯ«цЯ»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕ B Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»ЂЯ««Я»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ AB AB Я«јЯ«Е Я«хЯ«░Я«┐Я«џЯ»ѕ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«ЄЯ««Я»ЇЯ««Я»ЂЯ«▒Я»ѕ Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«ЄЯ««Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЋЯ»ІЯ«│Я««Я»ЂЯ««Я»Ї Я«цЯ«ЕЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«░Я»ЂЯ«ЋЯ«ЙЯ««Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ«ЕЯ»ѕЯ«џЯ»Ї Я«џЯ»ѓЯ«┤Я»ЇЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«єЯ«▒Я»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«Е. AAAA...... Я««Я»ЂЯ«▒Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ABAB....... Я««Я»ЂЯ«▒Я»ѕ Я«єЯ«ЋЯ«┐Я«»Я«ЕЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«њЯ«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ, ABAB...... Я««Я»ЂЯ«▒Я»ѕЯ«»Я«ЙЯ«ЕЯ«цЯ»Ђ Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«фЯ»ЇЯ«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ Я«јЯ«Е Я«еЯ«ЙЯ««Я»Ї Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«БЯ«░ Я««Я»ЂЯ«ЪЯ«┐Я«»Я»ЂЯ««Я»Ї.
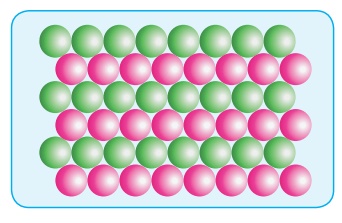
3. Я«јЯ«│Я«┐Я«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ
Я««Я»ЂЯ«фЯ»ЇЯ«фЯ«░Я«┐Я««Я«ЙЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї, Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї, AAAA Я«хЯ«ЋЯ»ѕ Я«ЄЯ«░Я»ЂЯ«фЯ«░Я«┐Я««Я«ЙЯ«Б Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕ Я«њЯ«цЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«њЯ«░Я»Ђ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ Я«јЯ«│Я«┐Я«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ, Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ««Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я«фЯ»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я»ЂЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«еЯ»ЄЯ«░Я«ЙЯ«Ћ Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я««Я»ЄЯ«▒Я»ЇЯ«фЯ»ЂЯ«▒Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е Я«јЯ«ЕЯ«хЯ»Є Я«ЄЯ«цЯ«ЕЯ»Ї Я«хЯ«┐Я«│Я»ѕЯ«хЯ«ЙЯ«Ћ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»ЂЯ««Я»Ї Я«њЯ«░Я»Є Я««Я«ЙЯ«цЯ«┐Я«░Я«┐Я«»Я«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«Е. Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ««Я»Ї, Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я«цЯ«┐Я«џЯ»ѕЯ«ЋЯ«│Я«┐Я«▓Я»ЂЯ««Я»Ї Я«њЯ«░Я»Є Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я«ЙЯ«Е Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«јЯ«│Я«┐Я«» Я«ЋЯ«ЕЯ«џЯ»Ї Я«џЯ«цЯ»ЂЯ«░ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«јЯ«│Я«┐Я«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЋЯ»ІЯ«│Я««Я»ЂЯ««Я»Ї, Я«цЯ«ЙЯ«ЕЯ»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ«ЕЯ»ѕЯ«џЯ»Ї Я«џЯ»ЂЯ«▒Я»ЇЯ«▒Я«┐ Я«ЁЯ«░Я»ЂЯ«ЋЯ«ЙЯ««Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«цЯ»іЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ»ЂЯ«ЪЯ«ЕЯ»Ї, Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«ЋЯ»ІЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«»Я»ЂЯ««Я»Ї, Я«ЋЯ»ђЯ«┤Я»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«ЋЯ»ІЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«јЯ«ЕЯ«хЯ»Є, Я«јЯ«│Я«┐Я«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«ЋЯ»ІЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«БЯ»ѕЯ«хЯ»Ђ Я«јЯ«БЯ»Ї 6.

Я«фЯ»іЯ«цЯ«┐Я«хЯ»ЂЯ«цЯ»Ї Я«цЯ«┐Я«▒Я«ЕЯ»Ї
Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«ЄЯ«ЪЯ»ѕЯ«хЯ»єЯ«│Я«┐Я«ЋЯ«│Я»Ї Я«ЋЯ«ЙЯ«БЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, Я«фЯ«▓ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ, Я«ЁЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»ЄЯ«»Я»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«хЯ»єЯ«│Я«┐Я«ЋЯ«│Я»Ї Я«ЈЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«њЯ«░Я»Ђ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«ЄЯ«ЪЯ««Я»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«њЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я««Я»іЯ«цЯ»ЇЯ«ц Я«ЋЯ«ЕЯ«ЁЯ«│Я«хЯ«ЙЯ«ЕЯ«цЯ»Ђ Я«ЁЯ«хЯ»ЇЯ«хЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«фЯ»іЯ«цЯ«┐Я«хЯ»ЂЯ«цЯ»Ї Я«цЯ«┐Я«▒Я«ЕЯ»ѕЯ«цЯ»Ї (Packing efficiency) Я«цЯ«░Я»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я««Я»ЂЯ«цЯ«▓Я«┐Я«▓Я»Ї Я«еЯ«ЙЯ««Я»Ї Я«њЯ«░Я»Ђ Я«јЯ«│Я«┐Я«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«фЯ»іЯ«цЯ«┐Я«хЯ»ЂЯ«цЯ»Ї Я«цЯ«┐Я«▒Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ЂЯ«хЯ»ІЯ««Я»Ї.
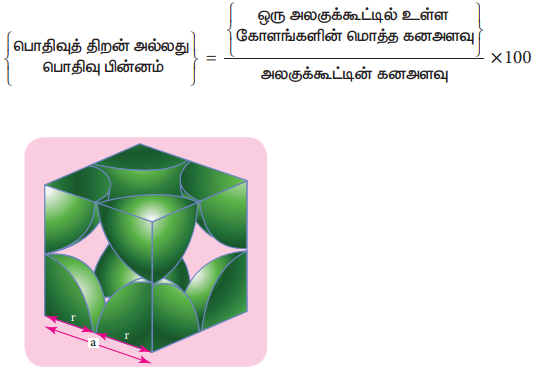
Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«хЯ«┐Я«│Я«┐Я««Я»ЇЯ«фЯ»Ђ Я«еЯ»ђЯ«│Я««Я»Ї 'a' Я«ЅЯ«ЪЯ»ѕЯ«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЂЯ«хЯ»ІЯ««Я»Ї. Я«хЯ«┐Я«│Я«┐Я««Я»ЇЯ«фЯ»Ђ Я«еЯ»ђЯ«│Я««Я»Ї a Я«ЅЯ«ЪЯ»ѕЯ«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЋЯ«ЕЯ«ЁЯ«│Я«хЯ»Ђ = a ├Ќ a ├Ќ a = a3 ... (1)
Я«ЋЯ»ІЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«єЯ«░Я««Я»Ї 'r' Я«јЯ«ЕЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї, Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ a=2r РЄњ r = a/2

Я«њЯ«░Я»Ђ Я«јЯ«│Я«┐Я«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї, Я«њЯ«░Я»Ђ Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ»іЯ«еЯ»ЇЯ«цЯ««Я«ЙЯ«Е Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ.

Я«ЃSc Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я»іЯ«цЯ»ЇЯ«ц Я«ЋЯ«ЕЯ«ЁЯ«│Я«хЯ»Ђ = 1 ├Ќ (¤ђ3/6) Рђд..(2)
(2) Я«љ (1) Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«Ћ,
Я«фЯ»іЯ«цЯ«┐Я«хЯ»Ђ Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ««Я»Ї = (¤ђa3/6) / (a3 ) ├Ќ 100= 100¤ђ / 6
=52.38%
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«јЯ«│Я«┐Я«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░ Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«фЯ»ЇЯ«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ«ЕЯ«ЁЯ«│Я«хЯ«┐Я«▓Я»Ї 52.38% Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«▓Я»Ї Я«еЯ«┐Я«░Я«фЯ»ЇЯ«фЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ, Я««Я»ђЯ«цЯ««Я»ЂЯ«│Я»ЇЯ«│ Я«ЄЯ«ЪЯ««Я»Ї Я«ЋЯ«ЙЯ«▓Я«┐Я«»Я«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«јЯ«ЕЯ«хЯ»Є Я«ЄЯ«хЯ»ЇЯ«хЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЁЯ«цЯ«┐Я«ЋЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ«ЙЯ«▓Я»Ї Я«ЁЯ«БЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ«┐Я«ЪЯ»ѕЯ«»Я»Є Я«хЯ«▓Я»ЂЯ«хЯ«ЙЯ«Е Я«ЋЯ«хЯ«░Я»ЇЯ«џЯ»ЇЯ«џЯ«┐ Я«ЈЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ«ЙЯ«»Я»ЇЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«хЯ«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
Я«цЯ«ЕЯ«┐Я«« Я«хЯ«░Я«┐Я«џЯ»ѕ Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЅЯ«▓Я»ІЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї, Я«фЯ»іЯ«▓Я»ЄЯ«ЕЯ«┐Я«»Я««Я»Ї Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Є Я«јЯ«│Я«┐Я«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«фЯ«ЪЯ«┐Я«ЋЯ««Я«ЙЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
4. Я«фЯ»іЯ«░Я»ЂЯ«│Я»Ї Я««Я»ѕЯ«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ
Я«ЄЯ«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї, Я««Я»ЂЯ«цЯ«▓Я»Ї Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«ЙЯ«Е Я«хЯ«ЋЯ»ѕ A Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»ѕЯ«»Я»іЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«еЯ»ЄЯ«░Я«ЪЯ«┐Я«»Я«ЙЯ«ЋЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ««Я«▓Я»Ї Я«џЯ«┐Я«▒Я«┐Я«цЯ»Ђ Я«хЯ«┐Я«▓Я«ЋЯ«┐ Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│Я«Е. Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ, Я«ЄЯ«еЯ»ЇЯ«ц A Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«ЈЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│ Я«ЄЯ«ЪЯ»ѕЯ«хЯ»єЯ«│Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ««Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ѕ Я«њЯ«цЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«фЯ«ЪЯ«┐Я«ЋЯ««Я»Ї Я««Я»ЂЯ«┤Я»ЂЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЄЯ«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЕЯ«цЯ»Ђ ABAB...... Я«јЯ«Е Я««Я»ђЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я««Я»ђЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«ЄЯ«хЯ»ЇЯ«хЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«ЄЯ«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«јЯ«еЯ»ЇЯ«ц Я«њЯ«░Я»Ђ Я«ЋЯ»ІЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«БЯ»ѕЯ«хЯ»Ђ Я«јЯ«БЯ»Ї 8 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«│Я««Я«ЙЯ«ЕЯ«цЯ»Ђ, Я«ЁЯ«цЯ»Ђ Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▒Я»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«ЄЯ«ЪЯ««Я»ЇЯ«фЯ»єЯ«▒Я»ЇЯ«▒Я»ЂЯ«│Я»ЇЯ«│ Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ»ЂЯ«ЪЯ«ЕЯ»Ї, Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«ЋЯ»ђЯ«┤Я»ЇЯ«фЯ»ЂЯ«▒Я««Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«цЯ»іЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЁЯ«БЯ»ѕЯ«хЯ»Ђ Я«јЯ«БЯ»Ї 8 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
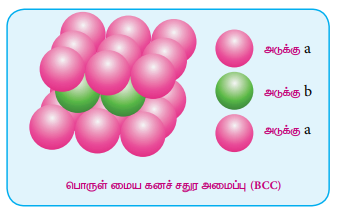
Я«фЯ»іЯ«цЯ«┐Я«хЯ»ЂЯ«цЯ»Ї Я«цЯ«┐Я«▒Я«ЕЯ»Ї
Я«ЄЯ«хЯ»ЇЯ«хЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї, Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«ЕЯ»ЇЯ««Я»ѕ Я««Я»ѓЯ«▓Я»ѕЯ«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«хЯ«┤Я«┐Я«»Я»Є Я«цЯ»іЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«Е.
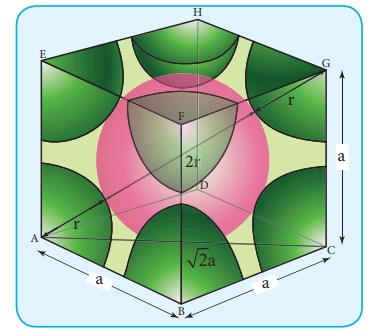

РѕєABCЯ«▓Я»Ї
AC2 = AB2 + BC2
AC = Рѕџ AB2 + BC2
AC = Рѕџ a2 + b2 = Рѕџ 2a2= Рѕџ2a
РѕєACGЯ«▓Я»Ї
AG2 = AC2 + CG2
AG = Рѕџ (Рѕџ2a)2 +a2
AG = Рѕџ 2a2 +a2 = Рѕџ 3a2
AG = Рѕџ 3a
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, Рѕџ 3a = 4r
r = Рѕџ 3/4 a
Я«Ѓ РђўrРђЎ Я«єЯ«░Я««Я»ЂЯ«ЪЯ»ѕЯ«» Я«ЋЯ»ІЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЋЯ«Е Я«ЁЯ«│Я«хЯ»Ђ
= 4/3¤ђ3
= 4/3¤ђ (Рѕџ3/4 a)3
= Рѕџ3/16 ¤ђ a3
bcc Я«хЯ«ЪЯ«┐Я«хЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«јЯ«Е Я«еЯ«ЙЯ««Я»Ї Я«ЁЯ«▒Я«┐Я«хЯ»ІЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«ЕЯ«ЁЯ«│Я«хЯ»Ђ

= 2 ├Ќ (Рѕџ3¤ђ a3 /16 ) = Рѕџ3¤ђ a3 /8 РђдРђд3
Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ (3) Я«љ (1) Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«Ћ,
Я«ЃЯ«фЯ»іЯ«цЯ«┐Я«хЯ»Ђ Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ««Я»Ї = (Рѕџ3¤ђ a3 / 8 / a3 ├Ќ 100
= Рѕџ3¤ђ / 8 ├Ќ 100
= Рѕџ3¤ђ ├Ќ 12.5
= 1.732 ├Ќ 3.14 ├Ќ 12.5
= 68 %
Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»Ї Я««Я»іЯ«цЯ»ЇЯ«ц Я«ЋЯ«ЕЯ«ЁЯ«│Я«хЯ«┐Я«▓Я»Ї 68% Я«ЋЯ«ЕЯ«ЁЯ«│Я«хЯ»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«▓Я»Ї Я«еЯ«┐Я«░Я««Я»ЇЯ«фЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«јЯ«│Я«┐Я«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»ЂЯ««Я»Ї Я«ЄЯ««Я»ЇЯ««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї, Я«ЁЯ«БЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я«ЙЯ«▓Я»Ї Я«ЁЯ«цЯ«┐Я«Ћ Я«ЋЯ«Е Я«ЁЯ«│Я«хЯ»Ђ Я«еЯ«┐Я«░Я«фЯ»ЇЯ«фЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ«ЙЯ«▓Я»Ї Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я»ѕЯ«хЯ«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
5. Я«ЁЯ«▒Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЂЯ«ЋЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я»ѕЯ«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ«▓Я»Ї
Я«ЄЯ«цЯ»ЇЯ«цЯ«ЋЯ»ѕЯ«» Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї, Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЕЯ«цЯ»Ђ, Я«ЄЯ«░Я»ЂЯ«фЯ«░Я«┐Я««Я«ЙЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї ABAB Я«хЯ«░Я«┐Я«џЯ»ѕ Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я««Я»ЂЯ«цЯ«▓Я»Ї Я«хЯ«░Я«┐Я«џЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЪЯ»ЂЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ђЯ«┤Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«хЯ»єЯ«│Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ««Я»Ї Я«хЯ«░Я«┐Я«џЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«ЄЯ«еЯ»ЇЯ«ц Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ѕ 'a' Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЂЯ«Ћ. Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«хЯ»єЯ«│Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ѕ 'b' Я«јЯ«ЕЯ»ЇЯ«Ћ .
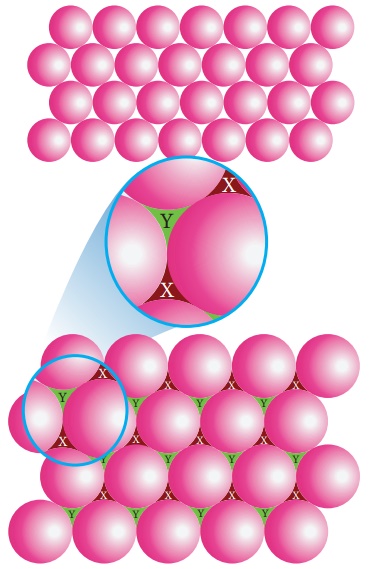
Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ«▓Я»Ї
Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ (a) Я«▓Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«ЋЯ»ѕЯ«»Я«ЙЯ«Е Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (Я«цЯ»ЂЯ«│Я»ѕЯ«ЋЯ«│Я»Ї )Я«ЋЯ«ЙЯ«БЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ, Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»ѕ x Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЂЯ«хЯ»ІЯ««Я»Ї.
Я«ЄЯ«еЯ»ЇЯ«ц Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ««Я»Ї / Я«цЯ»ЂЯ«│Я»ѕ, x Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ y Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«цЯ«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«ЪЯ»ѕЯ«хЯ»єЯ«│Я«┐ (Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ««Я»Ї) x Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«хЯ«┐Я«ЕЯ»ѕ Я«еЯ«ЙЯ««Я»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЂЯ«хЯ»ІЯ««Я»Ї.
Я««Я»ЂЯ«цЯ«▓Я«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ««Я»Ї x Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ Я«јЯ«ЎЯ»ЇЯ«ЋЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»єЯ«▓Я»ЇЯ«▓Я«ЙЯ««Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«ЕЯ«хЯ»І, Я«ЁЯ«ЎЯ»ЇЯ«ЋЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»єЯ«▓Я»ЇЯ«▓Я«ЙЯ««Я»Ї Я«њЯ«░Я»Ђ Я«еЯ«ЙЯ«ЕЯ»ЇЯ««Я»ЂЯ«ЋЯ«┐ Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ««Я»Ї (tetrahedral hole) Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«еЯ»ЇЯ«ц Я«еЯ«ЙЯ«ЕЯ»ЇЯ««Я»ЂЯ«ЋЯ«┐ Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ««Я»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«цЯ»Ђ Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ (a) Я«▓Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ (b) - Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«ЋЯ»ІЯ«│Я««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я»ѕЯ«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«еЯ«ЙЯ«ЕЯ»ЇЯ««Я»ЂЯ«ЋЯ«┐ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«цЯ«▓Я«ЙЯ«▓Я»Ї Я«ЄЯ«хЯ»ѕЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»ЄЯ«»Я«ЙЯ«Е Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ««Я»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ««Я»ЂЯ«ЋЯ«┐ Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ««Я»Ї Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«ЁЯ«цЯ»Є Я«еЯ»ЄЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї, Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ РђўaРђЎ Я«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»іЯ«░Я»Ђ Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ««Я«ЙЯ«Е 'y' Я«єЯ«ЕЯ«цЯ»Ђ Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї (b) Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«▓Я»Ї Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«│Я«хЯ»Ђ Я««Я«▒Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«цЯ«▒Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ ' Я«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЄЯ«цЯ»ЇЯ«цЯ«ЋЯ»ѕЯ«» Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«БЯ»ЇЯ««Я»ЂЯ«ЋЯ«┐ Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е.
Я«ЄЯ«еЯ»ЇЯ«ц Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ««Я»Ї Я«єЯ«▒Я»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«цЯ»Ђ. (Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЋЯ»ђЯ«┤Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ (a) Я«▓Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЄЯ«▓Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ (b)Я«▓Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї). Я«ЄЯ«еЯ»ЇЯ«ц Я«єЯ«▒Я»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я»ѕЯ«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ Я«јЯ«БЯ»ЇЯ««Я»ЂЯ«ЋЯ«┐ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«фЯ»Ї Я«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«ц Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ»іЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї/ Я«цЯ»ЂЯ«│Я»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ Я«ЁЯ««Я»ѕЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«фЯ»Ї Я«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«ц Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ 'n' Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«БЯ»ЇЯ««Я»ЂЯ«ЋЯ«┐ Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ n Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ««Я»ЂЯ«ЋЯ«┐ Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ 2n Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«ЄЯ«цЯ»Є Я«еЯ»ЄЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ (b) Я«▓Я»Ї Я«фЯ»ЂЯ«цЯ«┐Я«» Я«еЯ«ЙЯ«ЕЯ»ЇЯ««Я»ЂЯ«ЋЯ«┐ Я«цЯ»ЂЯ«│Я»ѕЯ«ЋЯ«│Я»Ї Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ (b) Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (a) Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«ЋЯ»ІЯ«│Я««Я»Ї Я«єЯ«ЋЯ«┐Я«»Я«ЕЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«▒Я»ЇЯ«ЋЯ«┐Я«ЪЯ»ѕЯ«»Я»Є Я«ЄЯ«еЯ»ЇЯ«ц Я«фЯ»ЂЯ«цЯ«┐Я«» Я«еЯ«ЙЯ«ЕЯ»ЇЯ««Я»ЂЯ«ЋЯ«┐ Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е.
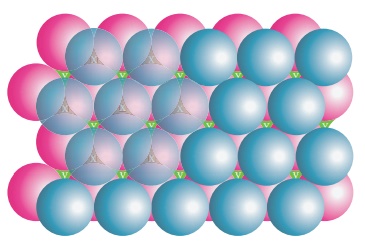
Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ«▓Я»Ї
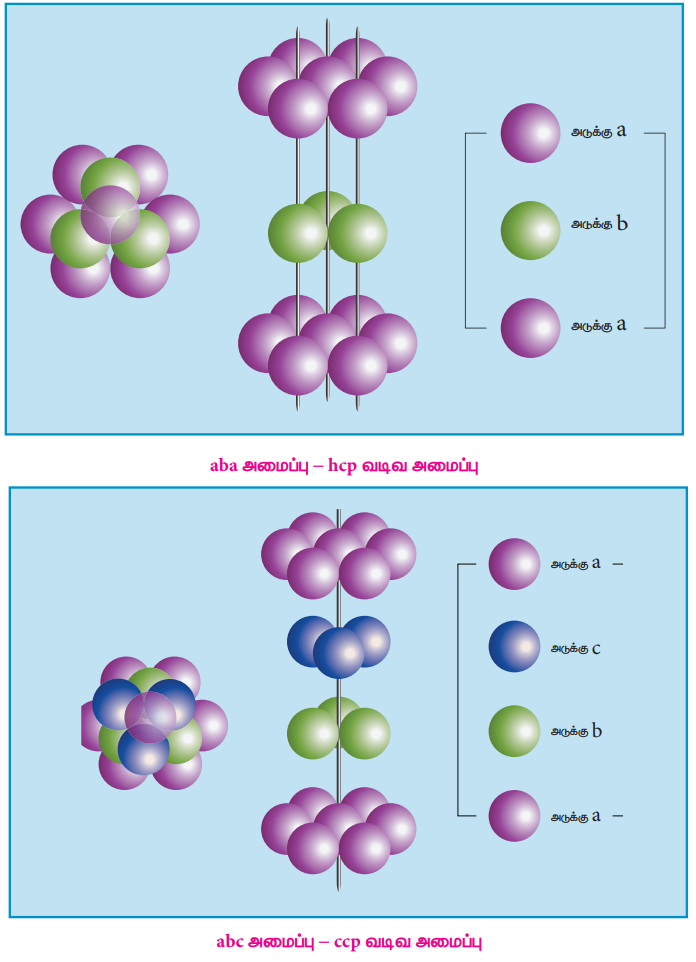
Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«фЯ»ЇЯ«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«ЄЯ«░Я»Ђ Я«хЯ«┤Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
(i) aba Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ - hcp Я«хЯ«ЪЯ«┐Я«х Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ
(ii) abc Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ - ccp Я«хЯ«ЪЯ«┐Я«х Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ
Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«хЯ»єЯ«│Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ»Ђ Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е 'a' Я«хЯ»ѕ Я«њЯ«цЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│Я«хЯ«ЙЯ«▒Я»Ђ Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«еЯ»ЇЯ«ц aba Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЕЯ«цЯ»Ђ, Я«ЁЯ«▒Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«фЯ»Ї Я«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ (hcp) Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ. Я«ЄЯ«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї, Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«еЯ«ЙЯ«ЕЯ»ЇЯ««Я»ЂЯ«ЋЯ«┐Я«цЯ»Ї Я«цЯ»ЂЯ«│Я»ѕЯ«ЋЯ«│Я»ѕ Я««Я«▒Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│Я«Е.
Я««Я«ЙЯ«▒Я«ЙЯ«Ћ, Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»Ї Я««Я»ЄЯ«▓Я»Ї, Я«јЯ«БЯ»ЇЯ««Я»ЂЯ«ЋЯ«┐Я«цЯ»ЇЯ«цЯ»ЂЯ«│Я»ѕЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«фЯ»іЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»ЂЯ««Я«ЙЯ«▒Я»Ђ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЕЯ«цЯ»Ђ Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я«ЙЯ«Е (a) Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї (b) Я«єЯ«ЋЯ«┐Я«»Я«ЕЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я««Я«ЙЯ«▒Я»ЂЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї, Я«ЄЯ«еЯ»ЇЯ«ц Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ (c) Я«јЯ«Е Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»Ђ abc abc ...... Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«ЁЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я«ЙЯ«▓Я»Ї Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░ Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«фЯ»ЇЯ«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ (ccp) Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
hcp Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї ccp Я«єЯ«ЋЯ«┐Я«» Я«ЄЯ«░Я»Ђ Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«фЯ»ЇЯ«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»ЂЯ««Я»Ї Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я»Ї Я«ЋЯ«ЙЯ«БЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«ЕЯ»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«ЁЯ«БЯ»ѕЯ«хЯ»Ђ Я«јЯ«БЯ»ЇЯ«БЯ»ЂЯ««Я»Ї 12 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«џЯ»Ї Я«џЯ»ѓЯ«┤Я»ЇЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«цЯ»Є Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«єЯ«▒Я»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї, Я««Я»ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ»ђЯ«┤Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«Е Я««Я»іЯ«цЯ»ЇЯ«ц 12 Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ«ЙЯ«▓Я»Ї Я«ЁЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«ЋЯ»ІЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«БЯ»ѕЯ«хЯ»Ђ Я«јЯ«БЯ»Ї 12 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»ЂЯ«хЯ»Є Я««Я«┐Я«ЋЯ«џЯ»Ї Я«џЯ«┐Я«▒Я«еЯ»ЇЯ«ц Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«фЯ»ЇЯ«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░ Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«фЯ»ЇЯ«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЕЯ«цЯ»Ђ Я««Я»ЂЯ«ЋЯ«фЯ»ЇЯ«фЯ»ЂЯ««Я»ѕЯ«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░ Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»ѕ Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«»Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«цЯ»Ђ. Я««Я»ЂЯ«ЋЯ«фЯ»ЇЯ«фЯ»ЂЯ««Я»ѕЯ«» Я«ЋЯ«ЕЯ«џЯ»ЇЯ«џЯ«цЯ»ЂЯ«░ Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї, Я«фЯ»іЯ«цЯ«┐Я«хЯ»ЂЯ«цЯ»Ї Я«цЯ«┐Я«▒Я«ЕЯ»ѕ Я«еЯ«ЙЯ««Я»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ЂЯ«хЯ»ІЯ««Я»Ї.
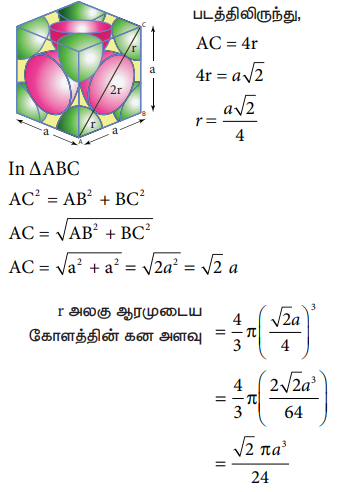
Я«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ,
AC = 4r
4r = aРѕџ2
r = aРѕџ2 / 4
In РѕєABC
AC2 = AB2 + BC2
AC = Рѕџ AB2 + BC2
AC = Рѕџ a2 + a2 = Рѕџ 2a2 = Рѕџ 2a
r Я«ЁЯ«▓Я«ЋЯ»Ђ Я«єЯ«░Я««Я»ЂЯ«ЪЯ»ѕЯ«» Я«ЋЯ»ІЯ«│Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЋЯ«Е Я«ЁЯ«│Я«хЯ»Ђ
= 4/3¤ђ (Рѕџ 2a/4)3
= 4/3¤ђ (2Рѕџ 2a3/64)
= Рѕџ2¤ђ a3 / 24

Я«њЯ«░Я»Ђ fcc Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЅЯ«░Я«┐Я«» Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ = 4
Я«Ѓfcc Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»ІЯ«│Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«ЕЯ«ЁЯ«│Я«хЯ»Ђ
= 4 ├Ќ (Рѕџ2¤ђ a3 / 24)
= (Рѕџ2 ¤ђ a3 / 6 ) РђдРђд4
Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ (4) Я«љ (1) Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«Ћ
Я«фЯ»іЯ«цЯ«┐Я«хЯ»ЂЯ«цЯ»Ї Я«цЯ«┐Я«▒Я«ЕЯ»Ї = (Рѕџ2¤ђ a3/ 6/ (a3) ├Ќ100
= Рѕџ2¤ђ /6 ├Ќ100
= 1.414 ├Ќ3.14├Ќ100/6
= 74%
Я«єЯ«░ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї (Radius ratio)
Я«ЁЯ«»Я«ЕЯ«┐Я«џЯ»Ї Я«џЯ»ЄЯ«░Я»ЇЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї, Я«ЁЯ«цЯ«┐Я«▓Я»Ї Я«ЁЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«»Я»ЂЯ«│Я»ЇЯ«│ Я«ЁЯ«»Я«ЕЯ«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЅЯ«░Я»ЂЯ«хЯ«│Я«хЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ»ЄЯ«цЯ«┐Я«хЯ«┐Я«ЕЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ѓЯ«▒Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї. Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Ћ Я«ЁЯ«»Я«ЕЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ«┐Я«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї, Я«фЯ»єЯ«░Я«┐Я«» Я«ЅЯ«░Я»ЂЯ«хЯ«│Я«хЯ»ЂЯ«│Я»ЇЯ«│ Я«јЯ«цЯ«┐Я«░Я«»Я«ЕЯ«┐Я«ЋЯ«│Я»Ї Я«еЯ»єЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«┐Я«фЯ»Ї Я«фЯ»іЯ«цЯ«┐Я«еЯ»ЇЯ«ц Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»ЂЯ««Я»Ї,Я«еЯ»ЄЯ«░Я«»Я«ЕЯ«┐Я«ЋЯ«│Я»Ї Я«ЁЯ«хЯ»ЇЯ«хЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«хЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»ЂЯ««Я»Ї Я«ЋЯ«ЙЯ«БЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«еЯ»ЄЯ«░Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«јЯ«цЯ«┐Я«░Я»Ї Я«ЁЯ«»Я«ЕЯ«┐ Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ѕЯ«»Я»ЄЯ«»Я«ЙЯ«Е Я«єЯ«░ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї (rC/rA) Я«єЯ«ЕЯ«цЯ»Ђ Я«фЯ«ЪЯ«┐Я«Ћ Я«хЯ«ЪЯ«┐Я«хЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ѕЯ«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ««Я«ЙЯ«ЕЯ«┐Я«фЯ»ЇЯ«фЯ«цЯ«┐Я«▓Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«фЯ»Ї Я«фЯ«ЎЯ»ЇЯ«ЋЯ«ЙЯ«▒Я»ЇЯ«▒Я»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я»Ї Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕЯ«»Я«ЙЯ«ЕЯ«цЯ»Ђ Я«єЯ«░Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«»Я«ЕЯ«┐Я«фЯ»Ї Я«фЯ«ЪЯ«┐Я«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«ЪЯ«┐Я«хЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»Ђ Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я«┐Я«▒Я»ЇЯ«ЋЯ«┐Я«ЪЯ»ѕЯ«»Я»ЄЯ«»Я«ЙЯ«ЕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ«┐Я«ЕЯ»ѕЯ«цЯ»Ї Я«цЯ«░Я»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
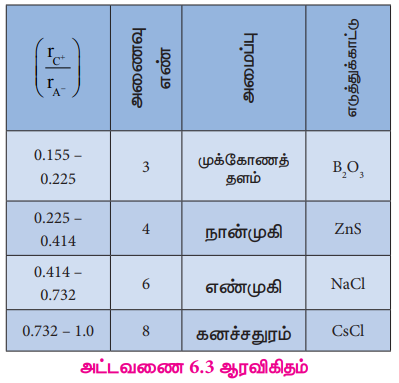
Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕ 6.3 Я«єЯ«░Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї