ஒரு வேதிவினையின் வினை வேகம்

ஒரு வேதிவினையின் வினை வேகம்

ஓரலகு காலத்தில் ஒரு குறிப்பிட்ட மாறியில் ஏற்படும் மாற்றம் வீதம் (rate) எனப்படும். இயற்பியல் பாடப்பகுதியில், ஓரலகு காலத்தில் ஒரு துகளின் இடப்பெயர்ச்சியில் ஏற்படும் மாற்றம் அதன் திசை வேகத்தைத் தரும் என தாங்கள் ஏற்கெனவே கற்றறிந்துள்ளீர்கள். அதைப்போலவே, ஓரலகு காலத்தில் ஒரு வேதிவினையில் இடம்பெற்றுள்ள வினைப்பொருட்களின் செறிவில் ஏற்படும் மாற்றம் அவ்வினையின் வினைவேகம் எனப்படுகிறது.

பின்வரும் பொதுவான எளிய வினை ஒன்றினைக் கருதுக.

A → B 

வினைபடு பொருளின் செறிவினை [A] வெவ்வேறு கால இடைவெளிகளில் கண்டறிய இயலும். அவ்வாறு t1 மற்றும் t2 ஆகிய இரு நேரங்களில் (t2 > t1) கண்டறியப்பட்ட A ன் செறிவுகள் முறையே [A1] மற்றும் [A2] எனக் கருதுவோம்.

இவ்வினையின் வினைவேகத்தினை பின்வருமாறு குறிப்பிடலாம்

வினைவேகம் = - [வினைபடு பொருட்களின் செறிவில் ஏற்படும் மாற்றம்] / [நேரத்தில் ஏற்படும் மாற்றம் ]

அதாவது வினைவேகம் = -([A2]-[A1]) / (t2-t1 ) =(∆[A] / ∆t ....(7.1) 

வினை நிகழும் போது, வினைபடு பொருட்களின் செறிவு குறையும் அதாவது [A2] < [A1] எனவே செறிவில் ஏற்படும் மாற்றம் [A2] - [A1]  ஆனது எதிர்க்குறி மதிப்பினைப் பெறும். வினைவேகமானது நேர்குறி மதிப்பினை உடையது என மரபு வழி கருதப்படுவதால், வினை வேகத்தைக் குறிப்பிடும் சமன்பாடு (7.1) ல் எதிர்க்குறி அறிமுகப்படுத்தப்பட்டுள்ளது.

வினைவிளை பொருட்களின் செறிவினை அளந்தறிவதன் மூலம் ஒரு வினை நிகழ்வதை நாம் கண்காணித்தால்,

வினைவேகமானது (∆[B] / ∆t ) ஆல்தரப்படுகிறது.

இந்நேர்வில் [B2] > [B1] என்பதால் இங்கு எதிர்க்குறி தேவையில்லை.

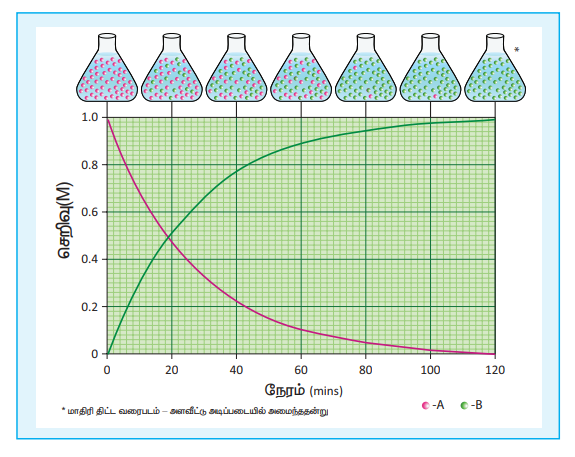
படம் 7.1 A → B என்ற வினையில் A மற்றும் B ஆகியனவற்றின் செறிவில் ஏற்படும் மாற்றம்

வினை வேகத்தின் அலகு 

வினைவேகத்தின் அலகு = செறிவின் அலகு / நேரத்தின் அலகு

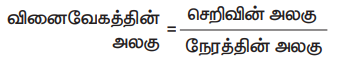
வழக்கமாக, செறிவானது ஒரு லிட்டரில் உள்ள மோல்களின் எண்ணிக்கையிலும் (mols per litre) நேரமானது வினாடிகளிலும் (seconds) குறிப்பிடப்படும். எனவே வினை வேகத்தின் அலகு mol L-1 S-1 வினையின் தன்மையினைப் பொருத்து, நிமிடம், மணி, ஆண்டு... போன்ற நேரத்தினைக் குறிக்கும் பிற அலகுகளும் பயன்படுத்தப்படுகின்றன.

ஒரு வாயுநிலை வினைக்கு, வாயுக்களின் செறிவானது வழக்கமாக அவைகளின் பகுதி அழுத்தங்களால் குறிப்பிடப்படுகின்றன. இத்தகைய நேர்வுகளில் வினை வேகத்தின் அலகு atm S-1 ஆகும். 

1. வேதிவினைக் கூறு விகிதம் மற்றும் வினையின் வேகம்

A → B என்ற வினையில், வினைபடு பொருள் மற்றும் வினைவிளை பொருள் ஆகிய இரண்டின் வேதிவினைக்கூறு விகிதங்களும் சமம். எனவே (A) ன் மறையும் வேகமும் (B) ன் உருவாகும் வேகமும் சமம்.

A → 2B என்ற வினையைக் மற்றொரு  கருதுவோம். 

இவ்வினையில், ஒவ்வொரு மோல் A மறையும் போதும், இரண்டு மோல்கள் B உருவாகிறது. அதாவது நன் உருவாதல் வேகமானது. Aன் மறைதல் வேகத்தைக் காட்டிலும் இருமடங்கு அதிகம். எனவே, வினை வேகமானது பின்வருமாறு குறிப்பிடப்படுகின்றது.

வினைவேகம் = +d[B] / dt = 2(-d[A] / dt)

மாறாக,

வினைவேகம் = -d[A] / dt = 1d[B] / 2 dt

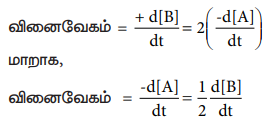
ஒரு பொதுவான வினைக்கு, வினைபடு பொருட்களின் வினைபடும் வேகம் (அல்லது) வினைவிளை பொருட்களின் உருவாதல் வேகம் ஆகியனவற்றை, அவ்வினையின் சமன்படுத்தப்பட்ட வேதிச் சமன்பாட்டிலுள்ள தொடர்புடைய வினைப்பொருட்களின் வேதிவினைக்கூறு விகித குணகங்களால் வகுப்பதன் மூலம் வினைவேகமானது பெறப்படுகிறது.

xA + yB → IC + mD 

வினைவேகம் = - 1 d[A] / xdt =  -1 d[B] / y dt =  1 d[C] / l dt = 1 d[D] / m dt

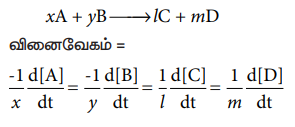
2. சராசரி மற்றும் ஒரு குறிப்பிட்ட நேரத்தில் வினைவேகம்

வளைய புரப்பேனின் மாற்றியமாதல் வினையினைக் கருத்திற் கொண்டு சராசரி மற்றும் ஒரு குறிப்பிட்ட நேரத்தில் வினைவேகம் ஆகியனவற்றை நாம் புரிந்து கொள்வோம்.

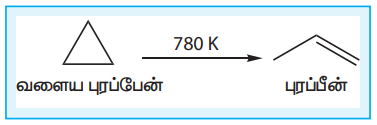
சீரான நேர இடைவெளிகளில், வளைய புரப்பேனின் செறிவினை அளந்தறிவதன் மூலம் இவ்வினையின் வினைவேகவியலானது அறியப்படுகிறது. பரிசோதனை முடிவுகள் பின்வருமாறு அட்டவணைப் படுத்தப்பட்டுள்ளன (அட்டவணை 7.1) 

அட்டவணை 7.1 780K வெப்பநிலையில் மாற்றியமாதல் வினை நிகழும் போது வெவ்வேறு நேரங்களில் வளைய புரப்பேனின் செறிவு. 

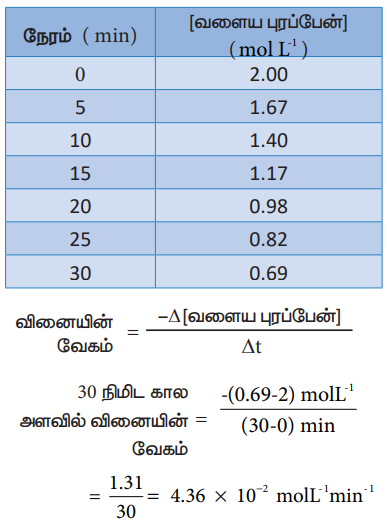
வினையின் வேகம் = ∆[வளைய புரப்பேன்] / ∆t

30 நிமிட கால அளவில் வினையின் வேகம் =  -(0.69-2) molL-1 / (30-0) min

              =1.31 /30  = 4.36 × 10-2 molL-1'min-1

வினை நிகழும் முதல் 30 நிமிடங்களில், வினைபடுபொருளான வளைய புரப்பேனின் செறிவு சராசரியாக ஒவ்வொரு நிமிடத்திற்கும் 4.36 × 10-2 mol L-1 என்ற அளவில் குறைந்து வருகிறது என இதன் மூலம் அறியலாம்.

வினையின் துவக்க நிலை மற்றும் பின்னர் ஏதேனும் ஒரு நேரத்தில் குறுகிய இடைவெளியில் வினையின் சராசரி வேகத்தினை நாம் கணக்கிடுவோம்.

(வினைவேகம்) ஆரம்ப நிலை =  -(1.4 - 2.0) / (10 –0)

                        = 0.6 /10 =  6x 10-2 mol L-1 min L-1

 (வினைவேகம்) பின்னர் ஏதேனும் ஒரு நிலை = -(0.69 - 0.98) / (30 – 20 )

                       = 0.29 / 10= 2.9 x 10-2 mol L-1 min L-1

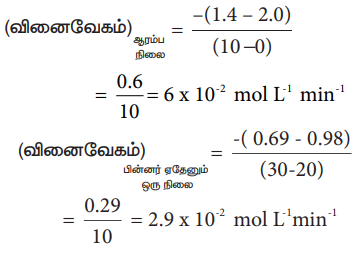
மேற்கண்டுள்ள கணக்கீடுகளில் இருந்து வினை தொடர்ந்து நிகழும் போது, நேரத்தைப் பொறுத்து வினைவேகம் குறைகிறது எனவும் , மேலும் எந்த ஒரு நேரத்திலும், வினையின் வேகத்தினை சராசரி வினைவேகத்தைக் கொண்டு தீர்மானிக்க இயலாது எனவும் நாம் அறிய முடிகிறது.

வினை நிகழும் போது, ஒரு குறிப்பிட்ட நேரத்தில் வினையின் வேகமானது அக்கணத்தில் வினைவேகம் (instantaneous rate) என அழைக்கப்படுகிறது. நாம் தேர்ந்தெடுக்கும் நேர இடைவெளியினைக் குறைத்துக் கொண்டே வரும் போது, வினைவேகத்தின் மதிப்பு, ஒரு குறிப்பிட்ட நேரத்தில் கண்டறியப்படும் வினைவேக மதிப்பினை நெருங்குகிறது.

∆t → 0; எனும்போது  ∆-[வளைய புரப்பேன்] / ∆t = -d (வளைய புரப்பேன்) / dt

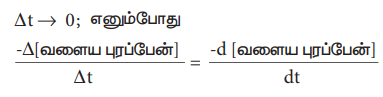
 (வளையபுரப்பேன்) vs நேரம்வரைபடமானது படம் 7.2ல் காட்டப்பட்டுள்ளது.

ஒரு குறிப்பிட்ட நேரம் ‘t’ ல் வினைவேகமானது -d (வளைய புரப்பேன்] / dt அந்நேரத்தில் வளைகோட்டிற்கு வரையப்படும் தொடுகோட்டினுடைய சாய்வின் மூலம் பெறப்படுகிறது.

பொதுவாக, வினைபடு பொருட்களை ஒன்றோடொன்று சேர்க்கும் நேரத்தில், (t = 0 எனும் போது) வரையப்படும் தொடுகோட்டின் சாய்வின் மூலம் பெறப்படும் வினைவேகத்தின் மதிப்பானது துவக்க வினைவேகத்தினைத் தருகிறது.

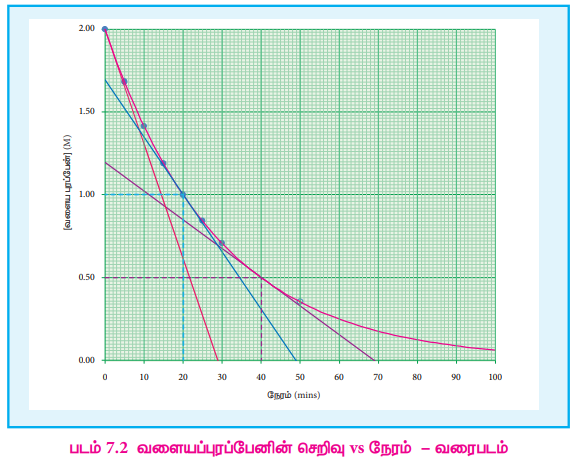
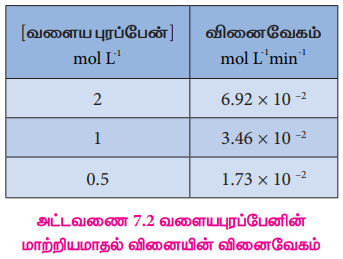
வளையபுரப்பேனின் மாற்றியமாதல் வினையில், ஒரு குறிப்பிட்ட நேரத்தில் அதாவது 2 M, 1M மற்றும் 0.5 M ஆகிய வெவ்வேறு செறிவுகளில் வினைவேகத்தினை படம் 7.2ல் தரப்பட்டுள்ள வரைபடத்திலிருந்து நாம் கணக்கிட இயலும். அவ்வாறு கண்டறியப்பட்ட மதிப்புகள் பின்வருமாறு அட்டவணைப்படுத்தப்பட்டுள்ளன.

3. வேக விதி மற்றும் வினைவேக மாறிலி

ஒரு வேதி வினையின் வேகமானது வினைபடு பொருட்களின் செறிவினைப் பொருத்து அமையும் என நாம் கற்றறிந்தோம். இப்பாடப்பகுதியில், ஒரு வினையின் வேகமானது அவ்வினையில் ஈடுபடும் வினைப்பொருட்களின் செறிவு மதிப்புகளோடு அளவியல் ரீதியாக எவ்வாறு தொடர்புபடுத்தப்படுகிறது என்பதனை பின்வரும் பொதுவான ஒரு வினையினைக் கருத்திற்கொண்டு நாம் புரிந்து கொள்வோம்.

xA + yB → விளைபொருள் 

மேற்கண்டுள்ள வினைக்கான பொதுவான ஒரு வேகவிதியினைபின்வருமாறு குறிப்பிடலாம். 

வினைவேகம் = k [A]m [B]n

இங்கு k என்பது விகித மாறிலியாகும். இது வினை வேக மாறிலி என அழைக்கப்படுகிறது. மேலும் m மற்றும் n என்பன முறையே A மற்றும் B ஆகியனவற்றைப் பொறுத்து வினைவகைகள் (order) ஆகும். வினையின் ஒட்டுமொத்த வினைவகை (m+n). செறிவு அடுக்குகளான m மற்றும் n ஆகியனவற்றைப் பரிசோதனைகளின் அடிப்படையில் மட்டுமே கண்டறிய இயலும் மேலும் அவ்வேதி வினையின் வேதி வினைக்கூறு விகித அடிப்படையில் கண்டறிய இயலாது. எடுத்துக்காட்டாக, நாம் ஏற்கெனவே விவாதித்த வளைய புரப்பேனின் மாற்றியமாதல் வினையினைக் கருத்திற் கொள்வோம்.

அட்டவணை 7.2ல் கண்டுள்ள சோதனை முடிவுகளின் படி, வளைய புரப்பேனின் செறிவினை பாதியாகக் குறைக்கும் போது, வினைவேகமும் பாதியாகக் குறைகிறது. அதாவது, வினைவேகமானது, வளைய புரப்பேனின் செறிவின் முதல் படிக்கு நேர்விகிதத்தில் உள்ளது. வினைவேகம் =k[ வளைய புரப்பேன்)

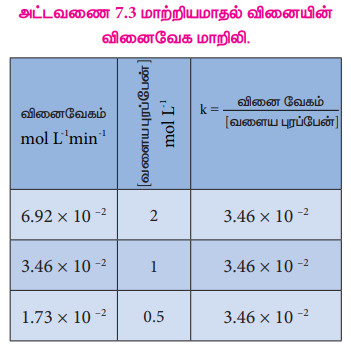
⇒ வினை வேகம் / (வளைய புரப்பேன்]= k

அட்டவணை 7.3 மாற்றியமாதல் வினையின் வினைவேக மாறிலி.

நைட்ரிக் ஆக்ஸைடு (NO) ஆக்சிஜனேற்றமடையும் வினையினை நாம் கருதுவோம்.

2NO(g) + O2 (g) → 2NO2 (g)

ஒரு வினைபடு பொருளின் செறிவினை மாறிலியாக வைத்து, மற்ற வினைபடு பொருட்களின் செறிவினை மாற்றியமைத்து தொடர்ச்சியாக சோதனைகள் மேற்கொள்ளப்பட்டன. அதன் முடிவுகள் பின்வருமாறு,

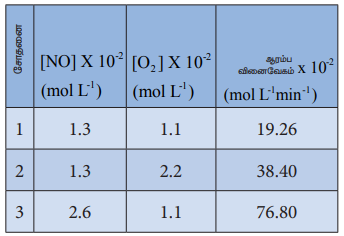
வினைவேகம் = k [NO]m [O2]n முதல் சோதனைக்கான வேக விதி

வேகம், = k [NO]m [O2]n 

19.26 X10-2 = k [1.3]m[1.1)n ... (1) இதைப்போலவே, சோதனை (2)ற்கு 

வேகம்2 = k [NO]m [O2]n 

38.40 X10-2 = k [1.3]m [2.2]n ...(2)

சோதனை (3)ற்கு வேகம்3 =k [NO]m [O2]n 

76.8 x 10-2 =k [2.6]m[1.1)n …… (3) 

(2) . (1) ppp 38.40 x 102 / 19.26 x 102 = k [1.3]m[2.2]n / k [1.3]m[1.1]n

2 = (2.2 / 1.1 ) n

2= 2n i.e; n=1

எனவே, வினையானது ஆக்சிஜனைப் O2 பொறுத்து முதல் வகை வினையாகும்.

(3) / (1) ppp 76.8 x 10-2 / 19.26 × 10-2 = k [2.6)m[1.1)n / k [1.3]m [1.1]n 

4=2m i.e., m=2

எனவே, வினையானது NO வைப் பொறுத்து இரண்டாம் வகை வினையாகும்.

வேக விதியானது வேகம் = k [NO]2[O2]1

ஒட்டுமொத்த வினைவகை = (2 + 1) = 3

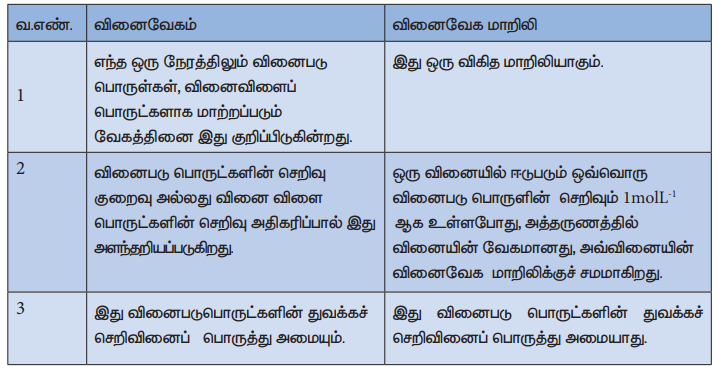
வினைவேகம் மற்றும் வினைவேக மாறிலி ஆகியவற்றிற்கிடையேயான வேறுபாடுகள்

வினைவேகம்

1. எந்த ஒரு நேரத்திலும் வினைபடு பொருள்கள், வினைவிளைப் பொருட்களாக மாற்றப்படும் வேகத்தினை இது குறிப்பிடுகின்றது.

2. வினைபடு பொருட்களின் செறிவு குறைவு அல்லது வினை விளை பொருட்களின் செறிவு அதிகரிப்பால் இது அளந்தறியப்படுகிறது.

3. இது வினைபடுபொருட்களின் துவக்கச் செறிவினைப் பொருத்து அமையும்.

வினைவேக மாறிலி

1. இது ஒரு விகித மாறிலியாகும்.

2. ஒரு வினையில் ஈடுபடும் ஒவ்வொரு வினைபடு பொருளின் செறிவும் 1molL-1ஆக உள்ளபோது, அத்தருணத்தில் வினையின் வேகமானது, அவ்வினையின் வினைவேக மாறிலிக்குச் சமமாகிறது.

3. இது வினைபடு பொருட்களின் துவக்கச் செறிவினைப் பொருத்து அமையாது.