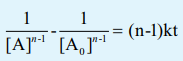தொகைப்படுத்தப்பட்ட வினைவேகச் சமன்பாடுகள் (The integrated rate equation)

தொகைப்படுத்தப்பட்ட வினைவேகச் சமன்பாடுகள் The integrated rate equation:

வினைவேகம், அதாவது வினைபடு பொருள்களின் செறிவு மாறுபாட்டு வீதமானது, அத்தருணத்தில் வினைபடுபொருள்களின் செறிவிற்கு நேர்விகிதத்தில் இருக்கும் என நாம் கற்றறிந்துள்ளோம். ஒரு பொதுவான வினைக்கு ,

A → விளைபொருள் வேக விதியானது,

வினைவேகம் =  -d[A] / dt = k [A]x

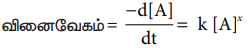
இங்கு k என்பது வினைவேக மாறிலி,

x என்பது வினைவகை. மேற்கண்டுள்ள சமன்பாடு ஒரு வகைக்கெழுச் சமன்பாடாகும். இச்சமன்பாட்டில் -d[A] / dt இடம் பெற்றுள்ளதால் இச்சமன்பாட்டினைப் பயன்படுத்தி எந்த ஒரு நேரத்திலும் வினைவேகத்தைக் கண்டறியலாம். எனினும் மேற்கண்டுள்ள சமன்பாட்டினைப் பயன்படுத்தி 

(i) ஒரு குறிப்பிட்ட அளவு வினைபடு பொருள் (A) வினைபுரிய எவ்வளவு நேரமாகும்? 

(ii) 't' நேரத்திற்குப் பின் வினைபடு பொருளின் செறிவு என்னவாக இருக்கும்? போன்ற வினாக்களுக்கு உரிய விடையினை நேரடியாக பெற இயலாது. 

எனவே, நேரத்தை ஒரு மாறியாகக் கொண்டிருக்கக்கூடிய வேக விதியின் தொகைப்படுத்தப்பட்ட சமன்பாடு வடிவத்தினை பெறுவதன் மூலம் நாம் மேற்கண்டுள்ளனவற்றிற்கு தீர்வு காண இயலும். 

1. ஒரு முதல் வகை வினைக்கான தொகைப்படுத்தப்பட்ட சமன்பாடு

ஒரு வினையின் வினைவேகமானது, அவ்வினையில் ஈடுபடும் வினைபடு பொருட்களின் செறிவுகளின் முதல் படியினைப் பொருத்து அமையுமானால், அவ்வினைகள் முதல் வகை வினைகள் எனப்படும். பின்வரும் முதல் வகை வினையினைக் கருதுக.

A → விளை பொருள்

வேக விதியானது வினைவேகம் =k[A]1 இங்கு k என்பது முதல் வகை வினையின் வினைவேக மாறிலி

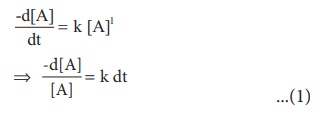
நேரம் t = 0 முதல் t = t என அமையும் நேர எல்லையில், வினைபடுபொருட்களின் மேற்கண்டுள்ள சமன்பாட்டினைத் தொகைப்படுத்த, செறிவு எல்லை [Ao] முதல் [A] ஆக அமைகிறது எனில், இந்த எல்லை மதிப்புகளில் 

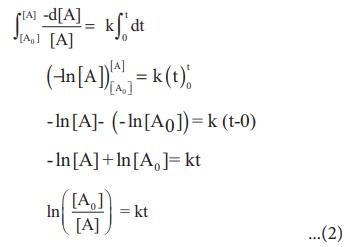
இச்சமன்பாடு இயல் மடக்கையில் அமைந்துள்ளது. இதனை வழக்கமான 10ஐ அடிமானமாகக் கொண்ட, மடக்கைக்கு மாற்ற சமன்பாட்டினை 2.303 ஆல் பெருக்க வேண்டும்.

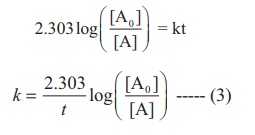
சமன்பாடு (2) ஐ y = mx + c என்ற வடிவில் பின்வருமாறு எழுதலாம்.

ln [A0 ] −ln [A] = kt

ln [A] = ln [A0 ] −kt

⇒ y = c + mx

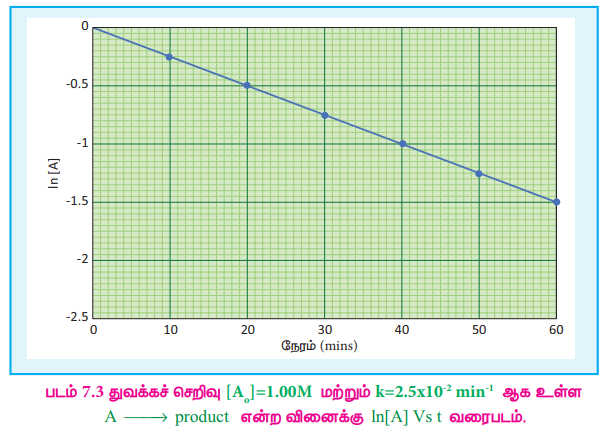
சீரான நேர இடைவெளிகளில், வினைபடு பொருட்களின் செறிவினைக் கண்டறிவதன் மூலம் வினை நிகழ்வதைக் கண்காணித்தால் அம்முடிவுகளின் அடிப்படையில் வரையப்படும், In[A] vs t வரைபடமானது எதிர்குறி சாய்வுடன் கூடிய நேர்கோட்டினைத் தரும். இதிலிருந்து வினை வேக மாறிலியின் மதிப்பினை நாம் கண்டறியலாம். 

முதல் வகை வினைக்கான எடுத்துக்காட்டுகள்

 (i) நைட்ரஜன் பென்டாக்ஸைடு சிதைவுறுதல், N2O5(g) → 2NO2 (g) + ½ O2 (g)

(ii) சல்பியூரைல் குளோரைடு சிதைவுறுதல், SO2C12(1) → SO2 (g) + C12(g) (iii) H2O2 ன் நீர்க்க ரைசல் சிதைவடைதல் H2O2 (aq) → H2O(1) + ½ O2 (g) (iv) வளைய புரப்பேனானது புரப்பீனாக மாற்றியமாதல். 

போலி முதல் வகை வினைகள்

உயர் வகைவினைகளின் வேதிவினைவேகவியல் ஆய்வுகள் சிக்கலானவை. எடுத்துக்காட்டாக, இரு வேறு வினைபடுபொருட்கள் வினைப்படும் ஒரு இரண்டாம் வகை வினையில் , இரு வினைபடுபொருட்களின் செறிவுகளில் ஏற்படும் மாறுபாடுகளை ஒரே நேரத்தில் கண்டறிதல் என்பது எளிதானதன்று. இத்தகைய நடைமுறைச் சிக்கல்களைத் தவிர்க்க, ஒரு இரண்டாம் வகை வினையில், ஏதேனும் ஒரு வினைபடுபொருளின் அளவினை மிக அதிக அளவில் எடுத்துக்கொள்வதன் மூலம் அவ்வினையினை முதல் வகை வினையாக மாற்றியமைக்கலாம். இவ்வாறு மாற்றியமைக்கப்படும் வினைகள் போலி முதல் வகை வினைகள் என அழைக்கப்படுகின்றன. அமில முன்னிலையில் எஸ்டர்களின் நீராற்பகுப்பினைக் கருதுவோம். 

CH3 COOCH3 (aq) + H2 O (l) → H + → CH3COOH (aq) + CH3OH (aq)

வினைவேகம் = k [CH3COOCH3] [H2O] 

இவ்வினையானது, அதிக அளவு நீரைக் கொண்டு நிகழ்த்தப்படின், நீராற்பகுத்தலின் போது, அதன் செறிவில் குறிப்பிடத் தகுந்த அளவு மாற்றம் ஏற்படுவதில்லை . அதாவது, ஏறத்தாழ நீரின் செறிவு மாறிலியாகும்.

இந்நிலையில், k [H2O] =k' என வரையறுக்க , எனவே மேற்கண்டுள்ள வேகச் சமன்பாடானது பின்வருமாறு மாற்றமடையும்.

வினைவேகம் = k' [CH3COOCH3]

எனவே இவ்வினை முதல்வகை வினையாகிறது. 

2. பூஜ்ய வகை வினைக்கான தொகைப்படுத்தப்பட்ட வேக விதி

செறிவு எல்லை முழுமைக்கும் ஒரு வினையின் வினைவேகமானது, வினைபடு பொருட்களின் செறிவினைப் பொருத்து அமையவில்லை எனில் அவ்வினை பூஜ்ய வகை வினை என அழைக்கப்படுகிறது. இத்தகைய வினைகள் அரிதானவை. பின்வரும் கருத்தியலான பூஜ்ய வகை வினையைக் கருத்திற் கொள்வோம்.

A → விளை பொருள் 

வேகவிதியினைப் பின்வருமாறு எழுதலாம். 

வினைவேகம் Rate = k [A]°

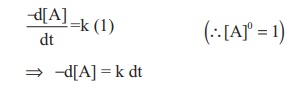
t = 0 எனும் போது செறிவு [Ao] மற்றும், t = t எனும் போது செறிவு [A] என அமையும் எல்லையில் மேற்கண்டுள்ள சமன்பாட்டை தொகையிட

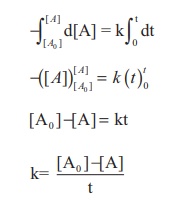
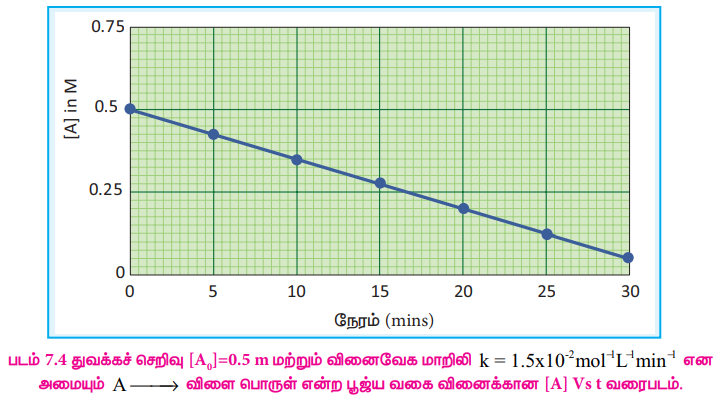
சமன்பாடு (2) ஆனது y = mx + c வடிவில் உள்ளது. அதாவது, [A] = kt + [A0]

⇒ y = c + mx

[A]vs நேரம் – வரைபடமானது 4 என்ற சாய்வு மதிப்பினையும், [A0] என்ற y- வெட்டுத்துண்டு மதிப்பினையும் பெற்றுள்ள ஒரு நேர்கோட்டினைத் தரும்.

பூஜ்ய வினைக்கான சான்றுகள்:

1. H2 மற்றும் C12 ஆகியவற்றிற்கிடையேயான  வேதிவினை. 

H2 (g)+Cl2 (g) →hv→2HCl(g)

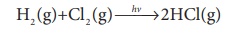
2. சூடான பிளாட்டினம் புறபரப்பில் N2O சிதைவடைந்து

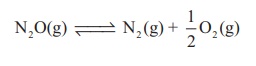
3. அசிட்டோன் அமில ஊடகத்தில் அயோடினேற்றம் அடைவது, அயோடினை பொருத்து பூஜ்ய வகை வினை

CH3 COCH3 + I2 → H+ →ICH2COCH3 + HI 

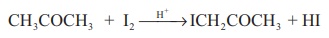
வினைவேகம் = k [CH3 COCH3] [H+]

A என்ற ஒரு வினைபொருள் மட்டுமே பங்கேற்கும் n^th வகை வினைக்கான பொதுவான வினைவேகச் சமன்பாடு

A → வினைபொருள்

வேகவிதி, -d[A] / dt = k[A]n

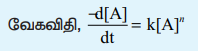
n≠1 எனும் நிலையைக் கருதுக. மேற்கண்டுள்ள சமன்பாட்டை t = 0 எனும் போது செறிவு [A0] ஆகவும் t = t எனும் போது செறிவு [A] ஆகவும் உள்ள எல்லையில் தொகையீடு செய்யும் போது பின்வரும் சமன்பாடு பெறப்படுகிறது.

1/[A]n-1 = 1/ [A0] n-1 = (n-1)kt