11வது இயற்பியல் : அலகு 3 : இயக்க விதிகள்
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்: இயற்பியல் : இயக்க விதிகள்
பயிற்சி கணக்குகள்
1. 20 Kg நிறையுள்ள பொருள் மீது 50N விசை படத்தில் காட்டியவாறு செயல்படுகிறது. x, y திசைகளில் பொருளின் முடுக்கங்களைக் காண்க.
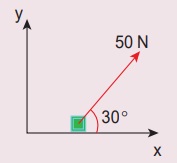
கொடுக்கப்பட்டவை m == 20kg,
F = 50N

விடை : ax=2.165 ms-2; ay=1.25 ms-2
2. 50g நிறையுள்ள சிலந்தி ஒன்று படத்தில் காட்டியவாறு அதன் வலையிலிருந்து தொங்குகிறது. வலையின் இழுவிசை யாது?

கொடுக்கப்பட்டவை நிறை m = 50 g
= 50 × 10-3 kg
வலையின் இழுவிசை T = mg
= 50 × 10-3 × 9.8
= 490 × 10-3
T = 0.49 N
விடை : T = 0.49N
3. கீழே காட்டப்பட்டுள்ள படத்திலிருந்து சுருள்வில் தராசு காட்டும் அளவீடு என்ன?
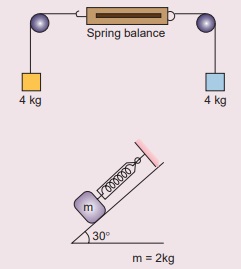
1) கொடுக்கப்பட்டவை m1 = 4Kg, m2 = 4kg
F1 = m1 g = 4 × 9.8 = 39.2N
F2 = m2 g = 4 × 9.8 = 39.2N
ஆனால் F1 = -F2
இரண்டு விசைகளும் சமமாகவும் எதிர் எதிராகவும் செயல்படுவதால் சுருள் வில் தராசு சுழி அளவீட்டிலேயே இருக்கும்.
2) கொடுக்கப்பட்டவை,
நிறை m = 2 kg, = 30°
F = mg sin θ = 2 × 9.8 × sin 30°
F = 2 × 9.8 × 1/2
F = 9.8N
சுருள் வில் தராசு காட்டும் அளவீடு 9.8 N
விடை : Zero, 9.8 N
4. மேசை ஒன்றின் மீது +1 இயற்பியல் தொகுதி 1 மற்றும் தொகுதி 2, +2 இயற்பியல் தொகுதி 1 மற்றும் தொகுதி 2 இவை வரிசையாக ஒன்றின் மீது ஒன்று அடுக்கி வைக்கப்பட்டுள்ளன
a) ஒவ்வொரு புத்தகத்தின் மீதும் செயல்படும் விசைகளைக் காண்க "தனித்த பொருள் விசை படங்கள்” அவற்றிற்கு வரைக.
b) ஒவ்வொரு புத்தகமும் மற்ற புத்தகங்கள் மீது தரும் விசைகளைக் கண்டுபிடி.
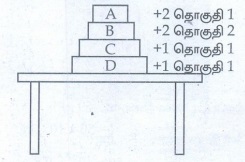
மேலே படத்தில் காட்டியள்ளவாறு +2 இயற்பியல் தொகுதிகள் 1 மற்றும் 2 முறையே A & B எனவும், +1 இயற்பியல் தொகுதிகள் 1 மற்றும் 2 முறையே C & D எனவும் ஒன்றின் மீது ஒன்றாக மேசையில் அடுக்கி கொள்வோம்.
+2 இயற்பியல் தொகுதி ஐ (BLOCK A) -ன் தனித்த விசைப்படம்.
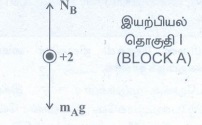
I. + 2 இயற்பியல் தொகுதி 1-ன் மீது செயல்படும் விசைகள் : (BLOCK A)
1. புவி ஏற்படுத்தும் கீழ் நோக்கிய ஈர்ப்பு விசை = MAg
2. +2 தொகுதி II (BLOCK B) ஏற்படுத்தும் மேற்நோக்கிய செங்குத்து எதிர்விசை = NB
+2 இயற்பியல் தொகுதி II (BLOCK B) -ன் தனித்த விசைப்படம்.
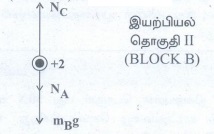
II. +2 இயற்பியல் தொகுதி II (BLOCK B) ன் மீதான விசைகள்:
1. கீழ்நோக்கி செயல்படும் புவிஈர்ப்பு விசை = mB g
2. +2 தொகுதி I (BLOCK A) ஏற்படுத்தும் கீழ்நோக்கிய விசை = NA
3. +1 தொகுதி I (BLOCK C) ஏற்படுத்தும் மேல்நோக்கிய செங்குத்து விசை = Nc
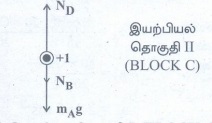
III. +1 இயற்பியல் தொகுதி I (BLOCK C) ன் மீதான விசைகள்
1. கீழ்நோக்கி செயல்படும் புவிஈர்ப்பு விசை = mcg
2. +2 தொகுதி II (BLOCK B) ஏற்படுத்தும் கீழ்நோக்கிய விசை = NB
3. +1 தொகுதி II (BLOCK D) ஏற்படுத்தும் மேல்நோக்கிய செங்குத்து விசை = ND

IV. +1 இயற்பியல் தொகுதி II (BLOCK D) ன் மீதான விசைகள்
1. கீழ்நோக்கி செயல்படும் புவிஈர்ப்பு விசை = mDg
2. +1 தொகுதி I (BLOCK C) ஏற்படுத்தும் கீழ்நோக்கிய விசை = Nc
3. மேசை ஏற்படுத்தும் மேல்நோக்கிய செங்குத்து விசை = Ntable
5. மெல்லிய கயிற்றில் கட்டப்பட்டுள்ள ஊசல் குண்டொன்று முன்னும் பின்னும் அலைவுறுகிறது. ஊசல் குண்டின்மீது செயல்படும் விசைகளைக் கூறுகளாகப் பிரிக்கவும். மேலும் θ கோணத்தில் அந்த ஊசல் குண்டு பெறும் முடுக்கத்தைக் கணக்கிடுக?
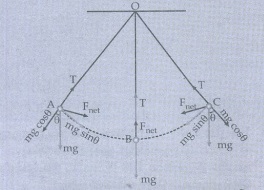
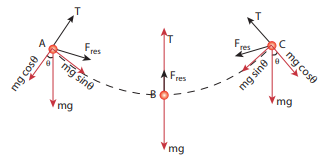
படத்தில் காட்டியுள்ளவாறு ஊசல் குண்டு பெரும் புவிஈர்ப்பு விசையை mg cos θ, mg sin θ எனப் பிரிக்கலாம்.
படத்தில் காட்டியுள்ளவாறு ஊசல் குண்டு ஒரு வட்டப்பாதையில் இயங்கு கிறது. எனவே இது θ கோணத்தில் ஊசல் குண்டு மைய நோக்கு முடுக்கத்தை பெறும்.
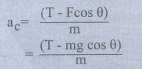
2) ஊசல் குண்டு A மற்றும் C புள்ளிகளில் கணநேர ஓய்வில் இருந்து பின்னர் ஃபுள்ளியை நோக்கிச் செல்லும்போது அதன் திசைவேகம் அதிகரிக்கும். ஊசல் குண்டு வட்டப்பாதையில் பெறும் தொடுகோட்டு முடுக்கம்.
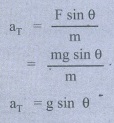
6. படத்தில் காட்டியவாறு m1 மற்றும் m2 இரண்டு நிறைகள் மெல்லிய கயிற்றினால் உராய்வற்ற கப்பியின் வழியே இணைக்கப்பட்டுள்ளன. மேசையுடனான m1 க்கும் மேசைக்கும் இடையேயான ஓய்வுநிலை உராய்வுக் குணகம் µs.m1 மீது எவ்வளவு சிறும நிறை m3 வைத்தால் m1 நகராது?
m1 = 15 kg, m2 = 10 kg, m3 = 25 Kg, µs = 0.2 எனில் உனது விடையை சரிபார்?

விடை:
படத்தில் இருந்து ஒவ்வொரு பொருளின் மீதான நிகரவிசை கீழ்கண்ட நிபந்தனைகளின் படி சுழியாகிறது
பொருள் A விற்கான நிபந்தனை
R= (m3 + m1) g -----------(1)
மேலும் T = fs = µsR
i.e. T = µs (m3 + m1) g
பொருள் B விற்கான நிபந்தனை
T = m2g (or)
µs (m3 + m1)g = m2g
ஃ m3 = m2-m1µs / µs ⇒ m2 / µs – m1
if m1 = 15 kg, m2 = 10 kg, µs = 0.2
m3 = 10 / 0.2 - 15
m3 = 50 – 15 = 35 kg
7. படம் 1 மற்றும் 2 இல் காட்டப்பட்ட 25 kg மிதி வண்டிகளின் முடுக்கங்களைக் கணக்கிடு.
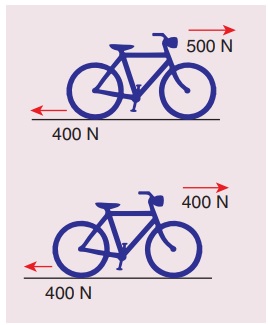
கொடுக்கப்பட்டவை நிறை m = 25 kg,
Fext = 500 N,
Ffric = 400N
1. படம் 1 நிகரவிசை Fnet = Fext - Ffric
= 500 - 400
Fnet = 100 N
முடுக்கம் a = Fnet/m
= 100/25
a = 4 ms-2
2. படம் 2 கொடுக்கப்பட்டவை நிறை
m=25 kg, Fext =400N, Ffric = 400N,
நிகரவிசை Fnet = Fext = Ffric
= 400 - 400
Fnet = 0
a = Fnet/m = 0/25 = 0
a = 0
விடை: a=4 ms-2, zero
8. படத்தில் காட்டப்பட்டுள்ள கவணிற்கு (கல்லெறி கருவி) லாமி தேற்றத்தை பயன்படுத்தி இழு கயிற்றின் இழுவிசையைக் காண்க?
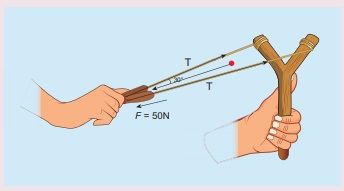
கொடுக்கப்பட்டவை, F = mg = 50N, θ = 30

T = 28.868 N
விடை: T = 28.868N.
9. கால்பந்து வீரரொருவர் 0.8 kg நிறையுடைய கால்பந்தை உதைத்து அதை 12 ms-1 திசை வேகத்தில் இயக்க வைக்கிறார். அவ்வீரர் வினாடியில் அறுபதில் ஒரு பங்கு நேரமே பந்தை உதைத்தார் எனில் அப்பந்தின் மீது அவர் செலுத்திய சராசரி விசையைக் காண்க.
கொடுக்கப்பட்டவை MB = 0.8 kg, u = 0,
v = 12ms-1 , t = 1/60 s
சராசரி விசை Favg = Δp/Δt
உந்த மாறுபாடு Δp =pf - pi
pf = Mv = 0.8 × 12 = 9.6 kg ms-1
pi = M × u = 0.8 × 0 = 0
Δp = 9.6 - 0 = 9.6 kg ms-1
Favg = Δp / Δt = 9.6 /1/60 = 9.6 × 60
Favg = 576 N
விடை: 576N.
10. 1 m நீளமுள்ள 2 Kg நிறையுள்ள கல் ஒன்று நூலில் கட்டப்பட்டு சுழல்கிறது. நூல் தாங்கக்கூடிய பெரும இழுவிசை 200 N. வட்ட இயக்கத்தில் கல் செல்லக்கூடிய பெரும வேகம் யாது?
கொடுக்கப்பட்டவை r = 1 m, m = 2kg, F = 200N

விடை: vmax=10ms-1
11. புவி மற்றும் நிலவு இவற்றிற்கிடையேயான ஈர்ப்பு விசை கண்ணுக்குப் புலப்படாத அவற்றை இணைக்கும் மெல்லிய கயிற்றின் வழி அளிக்கப் படுகிறது என்று கருதுக. புவி நிலாவிற்கு அளிக்கும் மையநோக்கு முடுக்கத்தால் ஏற்படும் இழு விசையை கணக்கிடுக.
(நிலாவின் நிறை = 7.34 × 1022 kg, புவிக்கும் நிலாவிற்கும் உள்ள தொலைவு = 3.84 × 108 m)
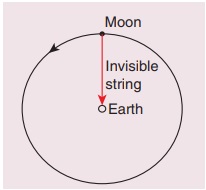
புவி நிலாவிற்கு அளிக்கும் மைய நோக்கு முடுக்கத்தால் ஏற்படும் இழுவிசை F = mv2/r
i.e. F = mam

= 7.34 × 1022 × 0.00272
= 1.99 × 1020
F = 2 × 1020 N
விடை: T = 2 x 1020 N.
12. 15kg, 10kg நிறை கொண்ட இரண்டு பொருட்கள் மெல்லிய கயிற்றின் மூலம் இணைக்கப்பட்டு வழுவழுப்பான தரையின் மீது வைக்கப் பட்டுள்ளன. படத்தில் காட்டியுள்ளவாறு F=500N விசையானது 15kg நிறை மீது செலுத்தப்பட்டால், கயிற்றின் மீது செயல்படும் இழுவிசையின் மதிப்பு என்ன?.
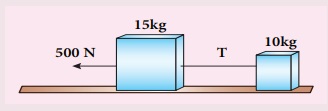
கொடுக்கப்பட்டவை, F = 500N
m1 = 15kg
m2 = 10 kg
விசை செயல்படுத்தப்படும் திசையில் அமைப்பின் மீதான முடுக்கம் a = F / m1 + m2
a = 500 / 15 + 10
a = 20 ms-2
கயிற்றின் மீது செயல்படும் இழுவிசை
T = m2a
= 10 × 20
T = 200N
விடை: T = 200N .
13. மக்கள் அடிக்கடி “எல்லா செயல்களுக்கும் சமமான எதிர்ச்செயல் உண்டு” என்று கூறுகிறார்கள். இங்கு செயல்கள்'' என்பது மனிதர்களின் செயல்களைக் குறிக்கிறது. மனிதர்களின் செயல்களுக்கு நியூட்டனின் மூன்றாம் விதியைப் பயன்படுத்துவது சரியா? நியூட்டனின் மூன்றாம் விதியில் குறிப்பிடப்படும் செயல் (Action) என்பது எதனைக் குறிக்கிறது?
விடை:
மனிதர்களின் செயல்களில் எங்கெல்லாம் அவர்களின் உடல்விசை பயன்படுத்தப்படுகிறதோ அங்கு மட்டுமே நியூட்டனின் மூன்றாம் விதியினைப் பயன்படுத்தலாம். ஆனால் அவர்களின் மனரீதியான உளவியல் செயல்களுக்கும், எண்ணங்களுக்கும் நியூட்டனின் மூன்றாம் விதியைப் பயன்படுத்த முடியாது.
14. 10m வளைவு ஆரம் கொண்ட வட்ட வடிவச் சாலையில் செல்லும் கார், 50ms-1 'திசைவேகத்தில் வளைகிறது. அக்காரினுள்ளே அமர்ந்திருக்கும் 60 kg நிறையுடைய மனிதர் உணரும் மையவிலக்கு விசையைக் காண்க.
கொடுக்கப்பட்டவை r = 10m, v = 50ms-1
m = 60kg

விடை: 15,000 N
15. தரையில் கிடைத்தளமாக வைக்கப்பட்டுள்ள கம்பு (Stick) ஒன்றிலிருந்து 10 m தொலைவில் உள்ள நபரால் 0.5 kg நிறை கொண்ட கல்லினை அக்கம்பில் படுமாறு வீசி எறியத் தேவைப்படும் சிறுமத் திசைவேகத்தைக் காண்க. (இயக்க உராய்வுக் குணகம் μk = 0.7 என்க.)
கொடுக்கப்பட்டவை m = 0.5 kg, S = 10m, u = 0
இயக்க உராய்வின் விசை fk = µkN (or) fk = µkmg -------------(1)
இயக்க உராய்வு எதிர்முடுக்கம் 'a' - வினால் ஏற்படுத்தப்படும் விசை fk = ma---------------------(2)
சமன்பாடு (1) மற்றும் (2) - லிருந்து
ma = µkmg
a = µkg
= 0.7 × 9.8
முடுக்கம் a = 6.86 ms-2
இயக்க சமன்பாடிலிருந்து
v2 - u2 = 2as
v2 - 0 = 2 × 6.86 × 10
ஃ சிறும திசைவேகம் v = 11.71 ms-1
கருத்துரு வினாக்கள்
1. கார் ஒன்றின் உள்ளே இருந்து அக்காரைத் தள்ள முடியாது ஏன்?
விடை:
● ஓய்வு நிலையில் உள்ள காரினுள் உள்ள ஒருவரால் காரைத் தள்ளுவதற்கு கொடுக்கப் படும் விசையானது அகவிசையாகும். அகவிசை யானது ஒருபோதும் பொருளில் இயக்கத்தை ஏற்படுத்தாது. எனவே கார் ஒன்றின் உள்ளே இருந்து காரைத் தள்ள முடியாது.
2. பரப்புகளை ஒரு குறிப்பிட்ட எல்லைக்கு மேல் வழுவழுப்பாக்கினால் அவற்றின் உராய்வுத்தடை குறைவதற்குப் பதிலாக அதிகரிப்பதன் காரணம் என்ன?
விடை:
● பரப்புகளை அளவுக்கதிகமாக வழுவழுப்பாக்கும் போது, பரப்புகளுக்கிடையேயான தொடுதல் பரப்பு அதிகரிக்கிறது.
● இதன் விளைவாக இரு பரப்புகளிலும் உள்ள அதிக எண்ணிக்கையிலான அணுக்களும் மூலக் கூறுகளும் வலிமையான கவர்ச்சி விசையை அவற்றின் இடையே ஏற்படுத்த துவங்குவதால் உராய்வுவிசை அதிகரிக்கப்பட்டு உராய்வுத் தடை அதிகரிக்க காரணமாகிறது.
3. ஒரே ஒரு தனித்த விசை இயற்கையில் தோன்றுமா?
விடை:
ஒரே ஒரு தனித்த விசை இயற்கையில் தோன்றாது. ஏனெனில் நியூட்டன் மூன்றாவது விதிப்படி ஒவ்வொரு விசைக்கும் அதற்கு சமமானது மற்றும் எதிரானதுமான விசை ஒன்று உண்டு. எனவே விசை எப்போதும் சோடியாகவே தோன்றும்.
4. பாராசூட் மெதுவாகக் கீழே விழுவதன் காரணம் என்ன?
விடை:
● அதிக தொடுதல் பரப்புகள் கொண்ட பொருட் களான பாராசூட் (அ) இறகு பந்து போன்றவை மெதுவாகவே கீழே இறங்கும். ஏனெனில் அப்பொருட்கள் அதிகப்படியான காற்று உராய்வுத்தடைக்கு உட்படுத்தப்படும்.
● இவ்வாறாக காற்றுத் தடை, உராய்வு விசை போன்றவை பொருட்கள் இயங்கும் திசைக்கு எதிர் திசையில் செயல்படுவதால் பாராசூட் கீழே இறங்கும் போது மெதுவாக இறங்குகிறது.
5. பனிக்கட்டி மீது நடக்கும்போது நெருக்கமாக அடி எடுத்து வைக்க வேண்டும் ஏன்?
விடை:
● பனிக்கட்டியின் மீது அதிக இடைவெளி கொண்டு நடக்கும் போது அதிகப்படியான முன்னோக்கு மற்றும் பின்னோக்கு விசை செயல்பட்டு கீழே விழுந்து விடலாம். ஆனால் நாம் குறைவான முன்னோக்கு மற்றும் நடக்க வேண்டுமானால் குறைவான இடை வெளியில் நடக்க வேண்டும்.
● எனவே பனிக்கட்டியில் நடக்கும் போது நெருக்கமாக அடி எடுத்து வைக்கவேண்டும். மேலும் இவ்வாறு நடக்கும் போது அதிக செங்குத்துவிசை செயல்பட்டு அதிக உராய்வு விசையை ஏற்படுத்தும்.
6. மனிதரொருவர் தரையில் நடக்கும்போது, மனிதரின் மீது செயல்படும் தரையின் உராய்வு விசை அவரின் இயக்கத்திசைக்கு எதிராகச் செயல்படும். சரியா? தவறா?
விடை:
● தவறு. மனிதரொருவர் தரையில் நடக்கும் போது அவரின் பாதமானது தரையில் பின்னோக்கி தள்ளப்படுகிறது.
● முன்னோக்கி நடந்து கொண்டிருக்கும் மனிதரொருவர் தரையின் மீது பின்னோக்கு விசை செயல்படுத்துவதால் பாதத்தின் மீது உராய்வு விசை முன்னோக்கி செயல்படுகிறது.
● எனவே உராய்வு விசையானது மனிதனின் இயக்க திசையிலே செயல்படுகிறது.
7. உராய்வுக் குணகம் ஒன்றை விட அதிகமாக இருக்க முடியுமா?
விடை:
● உராய்வுக் குணகம் ஒன்றை விட அதிகமாக இருக்க முடியாது. ஏனெனில் சமதள பரப்புகளுக்கு உராய்வுக் குணகமானது ஒன்றைவிட குறைவா கவே இருக்கும்.
● ஆனால் நுண்ணளவிலான மேடு, பள்ளங்களை கொண்டுள்ள சமதளமற்ற பரப்புகளில் உராய்வுக்குணகம் ஒன்றைவிட அதிகமாக இருக்கலாம்.
8. பொருள் மீது செயல்படும் விசையின் திசையைக் கொண்டு இயக்கத்திசையைக் கூற முடியுமா?
விடை:
ஆம் (கூற முடியும்), நியூட்டன் இரண்டாம் வீதமானது அப்பொருளின் மீது செயல் படுத்தப் படும் விசைக்கு நேர்விகிதத்திலும் விசையின் திசையிலேயே பொருளின் இயக்கத்திசையும் அமையும்.
9. துகள் அமைப்பின் உந்தம் எப்பொழுதும் மாறாது. சரியா, தவறா?
விடை:
சரி. நியூட்டன் இரண்டாம் விதிப்படி பொருளின் உந்தமாறுபாட்டு வீதமானது செயல் படுத்தப்படும் விசைக்கு நேர்விகிதத்தில் அமையும் எனவே துகள் அமைப்பின் மீது எந்தவொரு புறவிசையுமே செயல்படுத்தாத வரையில் துகள் அமைப்பின் மொத்த உந்தம் மாறாது.
நியூட்டன் விதிகளின் பயன்பாடு தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்
எடுத்துக்காட்டு 3.1
m நிறையுள்ள புத்தகம் ஒன்று மேசை ஒன்றின் மீது ஓய்வு நிலையில் உள்ளது.
1. புத்தகத்தின் மீது செயல்படும் விசைகள் யாவை?
2. புத்தகம் செலுத்தும் விசைகள் யாவை?
3. புத்தகத்தின் விசைப்படத்தை வரைக.
தீர்வு
1) புத்தகத்தின் மீது இரண்டு விசைகள் செயல்படுகின்றன. அவை
i. கீழ்நோக்கிச் செயல்படும் புவிஈர்ப்பு விசை (mg).
ii. புத்தகத்தின் மீது மேசையின் பரப்பு ஏற்படுததும் செங்குத்து விசை (N). இது மேல் நோக்கியத்திசையில் செயல்படும்.
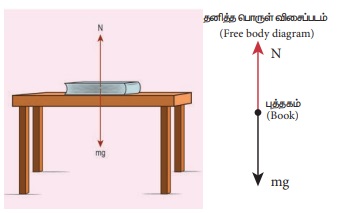
2) நியூட்டனின் மூன்றாம் விதிப்படி, புத்தகம் இரண்டு எதிர்விசைகளைத் தருகிறது.
i. புவியீர்ப்பு விசை (mg) க்கு எதிராக புத்தகம் புவியின்மீது செலுத்தும் விசை. இது மேல்நோக்கிச் செயல்படும்.
ii. மேசையின் பரப்புமீது, செங்குத்து விசை (N) க்கு எதிராக புத்தகம் செலுத்தும் விசை. இவ்விசை கீழ்நோக்கி செயல்படும்.
3. புத்தகத்தின் தனித்த பொருள் விசைப்படம் மேலே உள்ள படத்தில் காட்டப்பட்டுள்ளது.
எடுத்துக்காட்டு 3.2
2.5 kg மற்றும் 100 kg நிறையுடைய இரண்டு பொருள்களின் மீதும் 5 N விசை செயல்படுகிறது. ஒவ்வொரு பொருளின் முடுக்கத்தைக் காண்க.
தீர்வு
நியூட்டனின் இரண்டாம் விதிப்படி (எண்மதிப்பு அளவில்) F = ma
2.5 kg நிறையுடைய பொருள் பெறும் முடுக்கம்

ஆப்பிள், மரத்திலிருந்து கீழே விழும் போது அது புவி ஈர்ப்பு விசையை உணரும். நியூட்டனின் மூன்றாவது விதிப்படி ஆப்பிளும் இதற்குச் சமமான எதிர்விசையை புவியின் மீது செலுத்தும். இவ்விரண்டு விசைகளும் ஒன்றுக்கொன்று சமமாக இருப்பினும் அவைகள் பெரும் முடுக்கம் வெவ்வேறானவை.
புவியின் நிறை, ஆப்பிளின் நிறையுடன் ஒப்பிடும்போது மிகவும் அதிகம். எனவே, ஆப்பிள் மிக அதிக முடுக்கத்தைப் பெறுகிறது. ஆனால் புவி மிகவும் குறைவான புறக்கணிக்கதக்க முடுக்கத்தையே பெறுகிறது. எனவேதான் ஆப்பிள் கீழே விழும் போது புவி ஓய்வு நிலையில் உள்ளது போன்று தோன்றுகிறது.
எடுத்துக்காட்டு 3.3
படத்தில் காட்டப்பட்டுள்ள 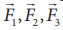 மூன்று விசைகளில் பெரும விசை எது?
மூன்று விசைகளில் பெரும விசை எது?
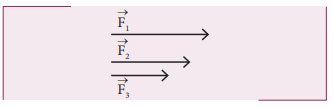
தீர்வு
விசை ஒரு வெக்டர். ஒரு வெக்டரின் எண் மதிப்பு அதன் நீளத்தால் குறிக்கப்படுகிறது. எனவே கொடுக்கப்பட்ட வெக்டர்களில் ![]() ன் நீளம் அதிகம் எனவே
ன் நீளம் அதிகம் எனவே ![]() வெக்டர் பெரும விசையாகும்.
வெக்டர் பெரும விசையாகும்.
எடுத்துக்காட்டு 3.4
400 g நிறை கொண்ட மாங்காய் ஒன்று மரத்தில் தொங்கிக் கொண்டிருக்கிறது. நியூட்டனின் இரண்டாம் விதியைப் பயன்படுத்தி மாங்காயைத் தாங்கியுள்ள காம்பின் இழுவிசையைக் காண்க.
தீர்வு
குறிப்பு: நியூட்டன் விதிகளைப் பயன்படுத்தும் போது பின்வரும் கருத்துக்களை கவனமுடன் பின்பற்ற வேண்டும்.
1. பொருத்தமான நிலைமக்குறிப்பாயம் ஒன்றைக் கருத வேண்டும். பொதுவாக புவியினை ஒரு நிலைமக்குறிப்பாயமாகக் கருதலாம்.
2. நியூட்டன் விதிகளைப் பயன்படுத்தத் தேவையான அமைப்பைக் கண்டறிய வேண்டும். அவ்வமைப்பானது ஒரு பொருள் அமைப்பாகவோ அல்லது ஒன்றுக்கு மேற்பட்ட பொருள்கள் சேர்ந்த அமைப்பாகவோ இருக்கலாம்.
3. பொருளின் மீது செயல்படும் விசைகளைக் கண்டறிந்து அவற்றைக் கொண்டு விசைப்படம் வரைய வேண்டும். பின்னர் நியூட்டனின் இரண்டாம் விதியை பயன்படுத்த வேண்டும். இடப்பக்கம் பொருளின் மீது செயல்படும் விசைகளை வெக்டர் வடிவில் குறிப்பிட வேண்டும். வலப்பக்கம் பொருளின் நிறை மற்றும் அப்பொருள் முடுக்கம் இவற்றின் பெருக்கல்பலனை வெக்டர் வடிவில் குறிப்பிட வேண்டும். ஏனெனில் முடுக்கம் ஒரு வெக்டர் அளவாகும்.
4. முடுக்கம் கொடுக்கப்பட்டிருப்பின் விசையைக் கண்டறியலாம். அதே போல் விசை கொடுக்கப்பட்டிருப்பின் பொருளின் முடுக்கத்தைக் காணலாம்.

மேலே கொடுக்கப்பட்டுள்ள கருத்துக்களின்படி படத்தில் காட்டியுள்ளவாறு தரையில் ஒரு நிலைமக் குறிப்பாயத்தைக் கருத வேண்டும்.
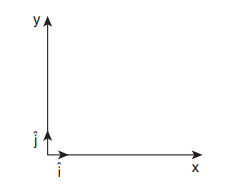
மாங்காயின் மீது பின்வரும் இரண்டு விசைகள் செயல்படுகின்றன.
i. மாங்காயின் மீது எதிர்க்குறி y அச்சுத்திசையில் கீழ் நோக்கி செயல்படும் புவியீர்ப்பு விசை, நேர்க்குறி y அச்சுத்திசையில் செயல்படும் மாங்காயைத் தாங்கியுள்ள காம்பு, மாங்காயின் மீது செலுத்தும் மேல் நோக்கிய இழுவிசை. மாங்காயின் விசைப்படம் கீழே காட்டப்பட்டுள்ளது.
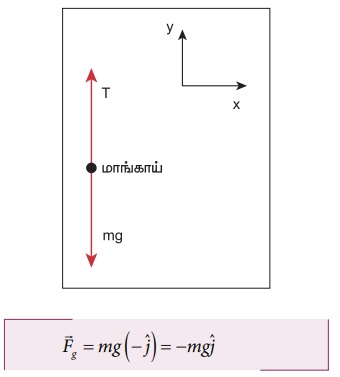
இங்கு mg என்பது புவியீர்ப்பு விசையின் எண்மதிப்பு மற்றும் ![]() என்பது எதிர்குறி y அச்சுத்திசையைக் குறிக்கும் ஓரலகுவெக்டர்.
என்பது எதிர்குறி y அச்சுத்திசையைக் குறிக்கும் ஓரலகுவெக்டர்.

எடுத்துக்காட்டு 3.5
இருசக்கர வாகனங்களில் தனித்தனியே பயணம் செய்யும் இருவரில், ஒருவர் தரையைப் பொருத்து மாறா திசைவேகத்தில் பயணம் செய்கிறார். மற்றொருவர் தரையை பொருத்து ![]() என்ற முடுக்கத்துடன் பயணம் செய்கிறார். இவ்விரண்டு பயணிகளில் எந்தப் பயணி நியூட்டனின் இரண்டாம் விதியைப் பயன்படுத்தலாம்?
என்ற முடுக்கத்துடன் பயணம் செய்கிறார். இவ்விரண்டு பயணிகளில் எந்தப் பயணி நியூட்டனின் இரண்டாம் விதியைப் பயன்படுத்தலாம்?
தீர்வு:
தரையைப் பொருத்து ![]() என்ற முடுக்கத்துடன் பயணம் செய்யும் நபர் நியூட்டன் இரண்டாம் விதியை பயன்படுத்த முடியாது. ஏனெனில் அவர் நிலைமக்குறிப்பாயத்தில் இல்லை. நிலைமக்குறிப்பாயத்தில் உள்ள பொருள் தானாக முடுக்கமடையாது. தரையை பொருத்து
என்ற முடுக்கத்துடன் பயணம் செய்யும் நபர் நியூட்டன் இரண்டாம் விதியை பயன்படுத்த முடியாது. ஏனெனில் அவர் நிலைமக்குறிப்பாயத்தில் இல்லை. நிலைமக்குறிப்பாயத்தில் உள்ள பொருள் தானாக முடுக்கமடையாது. தரையை பொருத்து ![]() என்ற மாறாத்திசை வேகத்துடன் பயணம் செய்யும் நபர் நியூட்டனின் இரண்டாம் விதியைப் பயன்படுத்தலாம் ஏனெனில் அவர் தரையைப் பொறுத்து நிலைமக் குறிப்பாயத்தில் பயணிக்கிறார்.
என்ற மாறாத்திசை வேகத்துடன் பயணம் செய்யும் நபர் நியூட்டனின் இரண்டாம் விதியைப் பயன்படுத்தலாம் ஏனெனில் அவர் தரையைப் பொறுத்து நிலைமக் குறிப்பாயத்தில் பயணிக்கிறார்.
எடுத்துக்காட்டு 3.6
துகளொன்றின் நிலை வெக்டர் 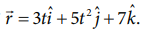 எந்த திசையில் இந்த துகள் நிகர விசையை உணர்கிறது?
எந்த திசையில் இந்த துகள் நிகர விசையை உணர்கிறது?
தீர்வு:

இங்கு, நேர்குறி y அச்சுத்திசையில் மட்டுமே துகள் முடுக்கமடையும். நியூட்டன் இரண்டாம் விதிப்படி நிகர விசையின் திசையும் நேர்குறி y அச்சின் திசையிலேயே அமையும். மேலும் இத்துகள் நேர்குறி x அச்சுத்திசையில் மாறாத் திசைவேகத்தைப் பெற்றுள்ளது. ஆனால் z அச்சுத்திசையில் எவ்வித திசைவேகத்தையும் பெறவில்லை. எனவே, x அல்லது z திசையில் எந்த நிகர விசையும் செயல்படவில்லை.
எடுத்துக்காட்டு 3.7
நீட்சித்தன்மையற்ற மெல்லிய கயிறு ஒன்றில் கட்டி தொங்கவிடப்பட்ட ஊசல்குண்டு ஒன்றைக் கருதுக. அதன் அலைவுகள் படத்தில் காட்டப்பட்டுள்ளது.
a) ஊசல் குண்டின் மீது செயல்படும் விசைகள் யாவை?
b) ஊசல்குண்டின் முடுக்கத்தினைக் காண்க.
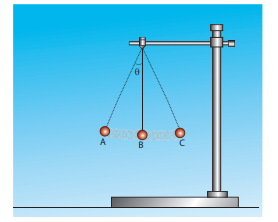
தீர்வு:
ஊசல் குண்டின் மீது பின்வரும் இரண்டு விசைகள் செயல்படுகின்றன அவை
i. கீழ் நோக்கிச் செயல்படும் புவி ஈர்ப்பு விசை (mg)
ii. குண்டின் மீது நூல் செலுத்தும் இழுவிசை (T).
இந்த இழுவிசையின் திசையை ஊசல்குண்டின் நிலை (position) தீர்மானிக்கிறது. அது பின்வரும் படத்தில் காட்டப்பட்டுள்ளது.
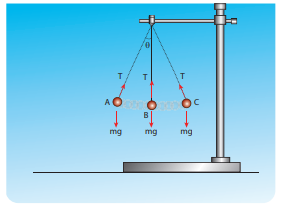
படத்தில் காட்டியுள்ளவாறு ஊசல்குண்டு ஒரு வட்டவில் பாதையில் இயங்குகிறது. எனவே இது ஒரு மைய நோக்கு முடுக்கத்தைப் பெறும். ஊசல் குண்டு A மற்றும் C புள்ளிகளில் கண நேர ஓய்வில் இருந்து, பின்னர் B புள்ளியை நோக்கிச் செல்லும்போது அதன் திசைவேகம் அதிகரிக்கும். எனவே, ஊசல்குண்டு வட்டவில் பாதையில் ஒரு தொடு கோட்டு முடுக்கத்தைப் பெறும். கீழே உள்ள படத்தில் காட்டியுள்ளவாறு புவியீர்ப்பு விசையை (mg cosθ, mg sinθ) என இருகூறுகளாகப் பிரிக்கலாம்.
எடுத்துக்காட்டு 3.8.
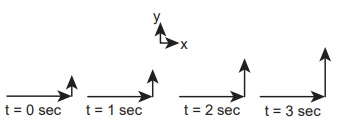
தளம் ஒன்றில் இயங்கும் துகளின் திசைவேகம் பின்வரும் படத்தில் காட்டப்பட்டுள்ளது. துகள் மீது செயல்படும் விசையின் திசையைக் காண்க.
தீர்வு:
துகளின் திசைவேகம் 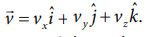 படத்தில் காட்டப்பட்டுள்ளது போன்று துகள் x y தளத்தில் இயங்குகிறது. z அச்சில் எவ்வித இயக்கமும் இல்லை. எனவே vz = 0.
படத்தில் காட்டப்பட்டுள்ளது போன்று துகள் x y தளத்தில் இயங்குகிறது. z அச்சில் எவ்வித இயக்கமும் இல்லை. எனவே vz = 0.
திசைவேகத்தின் x கூறு vx மற்றும் y கூறு vy என்க. t = 0 வினாடியிலிருந்து t = 3 வினாடிவரை உள்ள நேர இடைவெளியில் y அச்சுத்திசையில் வெக்டரின் நீளம் அதிகரிப்பதைக் காணலாம். எனவே y அச்சுத்திசையில் திசைவேகத்தின் கூறு (vy) நேரத்தைப் பொருத்து அதிகரிக்கிறது. நியூட்டனின் இரண்டாம் விதிப்படி y அச்சுத்திசையில் துகள் ஒரு முடுக்கத்தினைப் பெறும். எனவே y அச்சுத்திசையில் துகளின் மீது ஒரு விசை செயல்படும். x அச்சுத்திசையில் வெக்டரின் நீளம் மாறாமதிப்பினைப் பெற்றுள்ளது. இதன்மூலம் துகள் x அச்சில் மாறாத் திசைவேகத்துடன் இயங்குவதைக் காட்டுகிறது. எனவே x அச்சில் நிகர விசை சுழியாகும்.
எடுத்துக்காட்டு 3.9
புவிப்பரப்பில் ஓய்வு நிலையிலுள்ள பொருள் ஒன்றுக்கு நியூட்டனின் இரண்டாம் விதியினைப் பயன்படுத்தி அதன் மூலம் பெறப்படும் முடிவுகளை ஆராய்க.
தீர்வு:
நிலைமக்குறிப்பாயமாகக் கருதப்படும் புவியைப் பொருத்து பொருளொன்று ஓய்வு நிலையில் உள்ளது என்க. அப்பொருளின் மீது பின்வரும் இரண்டு விசைகள் செயல்படுகின்றன அவை,
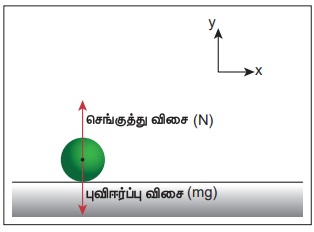
(i) எதிர்க்குறி y அச்சுதிசையில் செயல்படும் புவியீர்ப்பு விசை (mg)
(ii) நேர்க்குறி y அச்சுதிசையில் செயல்படும் புவிப்பரப்பு பொருளின் மீது செலுத்தும் மேல் நோக்கிய செங்குத்துவிசை (N). பொருளின் விசைப்படம் பின்வருமாறு.
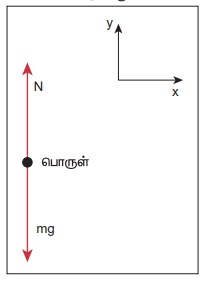

மேற்கண்ட சமன்பாட்டிலிருந்து நாம் அறிவது என்னவெனில், பொருள் ஓய்வு நிலையில் உள்ளபோது செங்குத்து விசையின் எண்மதிப்பும் புவியீர்ப்பு விசையின் எண்மதிப்பும் ஒன்றுக்கொன்று சமமாகும்.
எடுத்துக்காட்டு 3.10
2 kg நிறையுடைய பொருளின்மீது பின்வரும் இரண்டு விசைகள் செயல்படுகின்றன.

எடுத்துக்காட்டு 3.11
படத்தில் காட்டியுள்ள A, B மற்றும் C என்ற கனச் செவ்வகத்துண்டுகளின் மீது செயல்படும் விசைகளை காண்க.
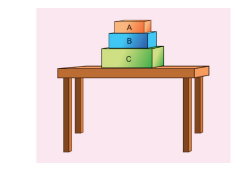
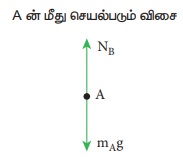
கனச்செவ்வகத்துண்டு A யின் மீது செயல்படும் விசைகள்:
(i) புவி ஏற்படுத்தும் கீழ்நோக்கிய ஈர்ப்பு விசை (mAg)
(ii) பொருள் B ஏற்படுத்தும் மேல் நோக்கிய செங்குத்து எதிர்விசை (NB)
A யின் “தனித்த பொருளின் விசைப் படம் கீழே காட்டப்பட்டுள்ளது.
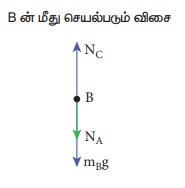
பொருள் B மீதான விசைகள்:
(i) கீழ்நோக்கிச் செயல்படும் புவியீர்ப்பு விசை (mBg)
(ii) கனச்செவ்வகத் துண்டு A ஏற்படுத்தும் கீழ்நோக்கிய விசை. (NA)
(iii) கனச்செவ்வகத் துண்டு C ஏற்படுத்தும் மேல்நோக்கிய விசை (NC)
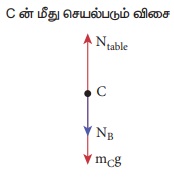
கனச்செவ்வகத் துண்டு C இன் மீது செயல்படும் விசை:
(i) கீழ்நோக்கிச் செயல்படும் புவியீர்ப்பு விசை (mCg)
(ii) கனச்செவ்வகத் துண்டு B ஏற்படுத்தும் கீழ்நோக்கிய விசை (NB)
(iii) மேசை ஏற்படுத்தும் மேல்நோக்கிய செங்குத்து விசை (Ntable)
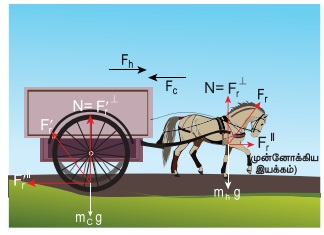
எடுத்துக்காட்டு 3.12
வண்டியில் கட்டப்பட்ட குதிரை ஒன்றைக் கருதுக. தொடக்கத்தில் அக்குதிரை ஓய்வு நிலையில் உள்ளது. குதிரை முன் நோக்கி நடக்கத் தொடங்கும்போது, வண்டி முன்நோக்கி ஒரு முடுக்கத்தைப்பெறும். Fh என்ற விசையுடன் குதிரை, வண்டியை முன்நோக்கி இழுக்கும். அதேநேரத்தில் நியூட்டனின் மூன்றாம் விதிப்படி வண்டியும், அதற்கு சமமான எதிர்திசையில் செயல்படும் (Fc = Fh) என்ற விசையுடன் குதிரையைப் பின்னோக்கி இழுக்கும். எனவே குதிரை மற்றும் வண்டி என்ற தொகுப்பின் விசை சுழியாக இருப்பினும் ஏன் குதிரை மற்றும் வண்டி முடுக்கமடைந்து முன்நோக்கி செல்கின்றன?
தீர்வு:
இம்முரண் கூற்றுக்குக் காரணம் நியூட்டனின் இரண்டாம் மற்றும் மூன்றாம் விதிகளை தவறாக பயன்படுத்துவதுதான். நியூட்டனின் விதிகளை பயன்படுத்துவதற்கு முன் அமைப்பினை (system) தீர்மானிக்க வேண்டும்.
இவ்வாறு அமைப்பினைக் கண்டறிந்த பின்னர் அவ்வமைப்பின் மீது செயல்படும் அனைத்து விசைகளையும் எளிதாகக் கண்டறியலாம். இங்கு அமைப்பு ஏற்படுத்தும் விசைகளைக் கருதக் கூடாது என்பதை நினைவில் கொள்ளவும். அமைப்பின் மீது ஏதேனும் சமன் செய்யப்படாத விசைகள் செயல்பட்டால், அமைப்பு தொகுபயன் விசையின் திசையில் முடுக்கமடையும். பின்வரும் கருத்துக்களை வரிசைப்படி பின்பற்றி குதிரை மற்றும் வண்டியின் இயக்கத்தைப் பகுப்பாய்வு செய்யலாம்.
குதிரை மற்றும் வண்டி இவை இரண்டையும் ஒன்றாக ஒரு அமைப்பு (system) என்று கருதினால் குதிரை, வண்டியின் மீது செலுத்தும் விசையையும், வண்டி குதிரையின் மீது செலுத்தும் எதிர்விசையையும் கருதக் கூடாது. மாறாக இந்த இரு விசைகளையும் அகவிசைகளாகக் கருத வேண்டும். மேலும் நியூட்டனின் மூன்றாம் விதிப்படி அகவிசைகளின் தொகுப்பயன் சுழி. அவை அமைப்பினை முடுக்கமடையச் செய்யாது. அமைப்பின் மீது ஏற்படும் முடுக்கம் புறவிசையால் மட்டுமே ஏற்படும். நாம் கருதும் இந்நிகழ்வில், சாலையானது அமைப்பின் மீது செலுத்தும் விசை புறவிசையாகும்.
அமைப்பின் மீது செயல்படும் அனைத்து விசைகளையும் கருதாமல் குதிரை மற்றும் வண்டியின் தொகுபயன்விசை சுழி என்று கருதுவது தவறாகும். சாலையானது, வண்டி - குதிரை அமைப்பை முன்னோக்கித் தள்ளுகிறது. வெளிப்புற விசை ஒன்று அமைப்பின் மீது செயல்படும் போது நியூட்டனின் மூன்றாம் விதியைப் பயன்படுத்தாமல் இரண்டாம் விதியைப் பயன்படுத்த வேண்டும். பின்வரும் படம் இதனை விளக்குகிறது.
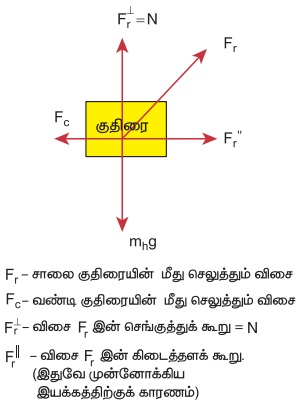
குதிரையை அமைப்பு என்று கருதினால், அதன்மீது பின்வரும் மூன்று விசைகள் செயல்படுகின்றன.
(i) கீழ்நோக்கிச் செயல்படும் புவியீர்ப்பு விசை (mng)
(ii) சாலை, குதிரையின் மீது செலுத்தும் விசை (Fr)
(iii) வண்டி, குதிரையின் மீது செலுத்தும் பின்னோக்கிய விசை (Fc)
இவை பின்வரும் படத்தில் காட்டப்பட்டுள்ளது. குதிரையின் மீது செயல்படும் விசைகள் சாலை, குதிரையின் மீது செலுத்தும் விசையை, கிடைத்தளக்கூறு மற்றும் செங்குத்துக் கூறு என இரண்டாகப் பிரிக்கலாம். செங்குத்துக்கூறு கீழ்நோக்கிச் செயல்படும் புவியீர்ப்பு விசையை சமன் செய்கிறது. முன்னோக்கிய திசையில் செயல்படும் கிடைத்தளக் கூறு பின்னோக்கிய விசை (Fc) ஐ விட அதிகம். எனவே முன்னோக்கியத் திசையில் ஒரு தொகுபயன் விசை செயல்பட்டு குதிரையை முன்னோக்கி இயக்குகிறது.
வண்டியை அமைப்பாகக் கருதினால், அதன்மீது பின்வரும் மூன்று விசைகள் செயல்படுகின்றன.
(i) கீழ்நோக்கிச் செயல்படும் புவியீர்ப்பு விசை (mcg)
(ii) சாலை, வண்டியின் மீது செலுத்தும் விசை ( Fr')
(iii) குதிரை, வண்டியின் மீது செலுத்தும் விசை (Fh)
இது பின்வரும் படத்தில் குறிப்பிட்டு காட்டப்பட்டுள்ளது.
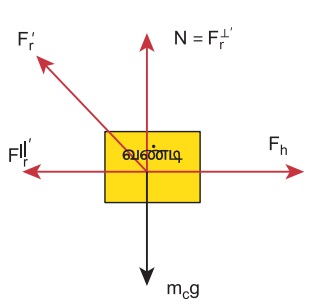
சாலை வண்டியின் மீது செலுத்தும் விசையை ( ![]() ) இரண்டு கூறுகளாகப் பிரிக்கலாம். செங்குத்துக் கூறு, கீழ்நோக்கியீர்ப்பு விசையை (mcg) சமன் செய்யும். கிடைத்தளக்கூறு பின்னோக்கிச் செயல்படும். மேலும் குதிரை, வண்டியின் மீது செலுத்தும் விசை (
) இரண்டு கூறுகளாகப் பிரிக்கலாம். செங்குத்துக் கூறு, கீழ்நோக்கியீர்ப்பு விசையை (mcg) சமன் செய்யும். கிடைத்தளக்கூறு பின்னோக்கிச் செயல்படும். மேலும் குதிரை, வண்டியின் மீது செலுத்தும் விசை (![]() ) முன்னோக்கிச் செயல்படும்.
) முன்னோக்கிச் செயல்படும்.
இது பின்னோக்கிச் செயல்படும் கிடைத்தளக் கூறைவிட அதிகம். எனவே, முன்நோக்கியத் திசையில் ஒரு தொகுபயன் விசை கிடைக்கும். இதன் காரணமாக வண்டி முன்னோக்கி முடுக்கமடையும்.
குதிரை மற்றும் வண்டி இரண்டையும் ஒரு அமைப்பாகக் கருதினால், இவ்வமைப்பின் மீது இரண்டு விசைகள் செயல்படும். அவை பின்வருமாறு
(i) கீழ்நோக்கிச் செயல்படும் புவியீர்ப்பு விசை (mh + mc)g
(ii) சாலை, அமைப்பின் மீது செலுத்தும் விசை (Fr) இவை, பின்வரும் படத்தில் காட்டப்பட்டுள்ளன.
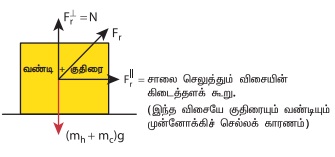
(iii) இந்நிகழ்வில், சாலை, அமைப்பின் மீது ஏற்படுத்தும் விசையை (Fr) இரு கூறுகளாகப் பிரிக்கலாம்.
(iv) சாலை, அமைப்பின் மீது செலுத்தும் விசையின் சமன் செய்யப்படாத கிடைத்தளக்கூறு, குதிரை மற்றும் வண்டி அமைப்பு முன்னோக்கிச் செல்வதற்கு காரணமாக அமைகிறது.
செங்குத்துக்கூறு புவியீர்ப்பு விசை (mh + mc)g யை சமன் செய்யும்.
எடுத்துக்காட்டு 3.13
y = ut – 1/2 gt2 என்ற சமன்பாடு துகள் ஒன்றின் நிலையைக் குறிக்கிறது.
(a) அத்துகளின் மீது செயல்படும் விசை மற்றும்
(b) அத்துகளின் உந்தத்தைக் காண்க.
தீர்வு
துகளின் மீது செயல்படும் விசையைக் காண அத்துகள் அடையும் முடுக்கத்தைக் கணக்கிட வேண்டும்.

விசை, எதிர்குறி y அச்சுத்திசையில் செயல்படுவதை எதிர்குறி காட்டுகிறது. மேலும் இதே விசைதான் எறிபொருள் ஒன்றின் மீது செயல்படும் விசையாகும்.
லாமி தேற்றத்தின் பயன்பாடு தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்
எடுத்துக்காட்டு 3.14
ஒத்த இரண்டு சங்கிலிகளால் செய்யப்பட்ட ஓய்வு நிலையில் உள்ள ஒரு ஊஞ்சல் ஒன்றில் குழந்தை ஒன்று அமர்ந்திருக்கிறது. அக்குழந்தையின் மீது செயல்படும் விசைகளைக் காண்க. மேலும் லாமியின் தேற்றத்தைப் பயன்படுத்தி சங்கிலியின் இழுவிசையைக் கணக்கிடுக.
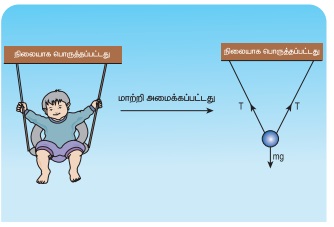
தீர்வு:
ஊஞ்சலில் அமர்ந்திருக்கும் குழந்தையை, நிறை ஒன்று நீட்சித்தன்மையற்ற மெல்லிய இரண்டு கயிறுகளால் கட்டித் தொங்கவிடப்பட்ட அமைப்பாகக் கருதலாம். குழந்தையின் மீது இரண்டு விசைகள் செயல்படுகின்றன. அவை
(i) எதிர்குறி y அச்சுத் திசையில் செயல்படும் கீழ்நோக்கிய புவியீர்ப்பு விசை (mg)
(ii) இரண்டு கயிறுகளின் வழியே செயல்படும் இழுவிசைகள் (T)
இவ்விரண்டு விசைகளும் படத்தில் காட்டியுள்ளபடி ஒருதள மற்றும் ஒருமைய விசைகளாகும்.
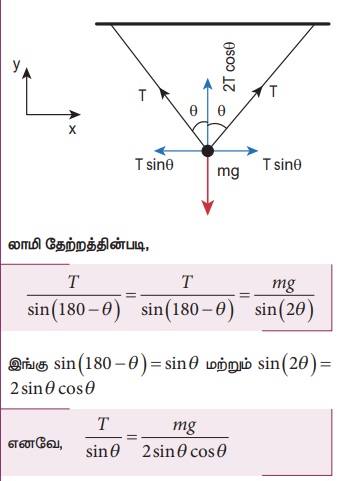
இதிலிருந்து ஒவ்வொரு கயிற்றின் இழுவிசை (T) பின்வருமாறு காணப்படும் T = mg / 2cosθ
எடுத்துக்காட்டு 3.15
கீழ்க்கண்ட அமைப்புகளில் செயல்படும் அக மற்றும் புற விசைகளை காண்க.
a) புவியை மட்டும் தனியாகக் கொண்ட அமைப்பு
b) புவி மற்றும் சூரியன் இணைந்த அமைப்பு
c) நடக்கும் மனிதன் - என்ற அமைப்பு
d) நமது உடல் மற்றும் புவி இணைந்த அமைப்பு
தீர்வு
(a) புவி மட்டும் கொண்ட அமைப்பு
சூரியனின் ஈர்ப்பு விசையினால், புவி சூரியனைச் சுற்றிவருகிறது. புவியினைத் தனித்த அமைப்பு எனக்கருதினால், சூரியனின் ஈர்ப்பு விசையை புறவிசையாகக் கருதலாம். நிலவையும் நாம் கணக்கில் எடுத்துக்கொண்டால், நிலவும் புவியின் மீது ஒரு புறவிசையைச் செலுத்தும்.
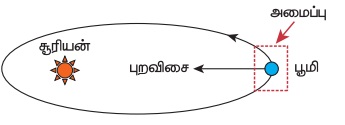
(b) புவி மற்றும் சூரியன் இணைந்த அமைப்பு
இந்நேர்வில், இரண்டு அக விசைகள் செயல் - எதிர்ச்செயல் விசை சோடியாக செயல்படுகின்றன. ஒன்று சூரியன் புவியின் மீது செலுத்தும் ஈர்ப்பு விசை, மற்றொன்று புவி சூரியனின் மீது செலுத்தும் ஈர்ப்புவிசை ஆகும்.
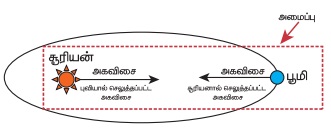
(c) நடக்கும் மனிதன் - என்ற அமைப்பு
நடக்கும் போது, நாம் புவியின் மீது ஒரு விசையை செலுத்தும் அதே நேரத்தில் புவியும் இதற்குச்சமமான எதிர்விசை ஒன்றை நம்மீது செலுத்துகிறது. நமது உடலை மட்டும் ஒரு அமைப்பாகக் கருதினால் புவி நம்மீது செலுத்தும் எதிர்விசையை புறவிசை எனக்கருதலாம்.
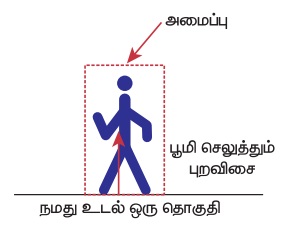
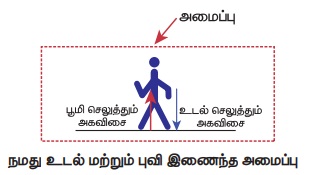
(d) நமது உடல் மற்றும் புவி இணைந்த அமைப்பு
இந்நிகழ்வில், இரண்டு அக விசைகள் அமைப்பில் உள்ளன. ஒன்று நாம் புவியின் மீது செலுத்தும் விசை, மற்றொன்று புவி நம்மீது செலுத்தும் சமமான எதிர்விசை.
உந்த மாறா விதியின் பொருள்
1) உந்த மாறா விதி ஒரு வெக்டர் விதியாகும். இவ்விதி மொத்த நேர்க்கோட்டு உந்தத்தின் எண் மதிப்பு மற்றும் திசை மாறாதவை எனக்காட்டுகிறது. சில நேர்வுகளில் மொத்த நேர்க்கோட்டு உந்தம் சுழி மதிப்பையும் பெறலாம்.
2) பொருளொன்றின் இயக்கத்தினைப் பகுப்பாய்வு செய்யும்போது நியூட்டனின் இரண்டாம் விதி அல்லது நேர்க்கோட்டு உந்த மாறா விதியை நாம் பயன்படுத்தலாம். நியூட்டனின் இரண்டாவது விதியைப் பயன்படுத்த வேண்டுமானால் நாம் பொருளின் மீது செயல்படும் விசைகளைக் குறிப்பிட வேண்டும். நடைமுறைச் சூழலில் இது கடினமாகும். ஆனால் உந்த மாறா விதியில், இவ்வாறு விசைகளைச் சுட்டிக்காட்ட வேண்டிய அவசியமில்லை. எனவே உந்த மாறா விதி பயன்படுத்துவதற்கு எளிமையானது மற்றும் முக்கியத்துவம் வாய்ந்ததாகும்.
எடுத்துக்காட்டாக, இரண்டு பொருட்கள் ஒன்றுடன் ஒன்று மோதும் நிகழ்வில் அவ்விரண்டு பொருட்களும் ஒன்றின்மீது மற்றொன்று செலுத்தும் விசையைக் குறிப்பிடுவது சற்றே கடினமாகும். ஆனால் மோதலின்போது உந்த மாறா விதியை பயன்படுத்துவது எளிமையாகும்.
எடுத்துக்காட்டுகள்
(1) துப்பாக்கி சுடும் நிகழ்வு ஒன்றைக் கருதுக. இங்கு துப்பாக்கி மற்றும் குண்டு இரண்டும் சேர்ந்தது ஒரு அமைப்பு ஆகும். தொடக்கத்தில் துப்பாக்கி மற்றும் குண்டு இரண்டும் ஓய்வு நிலையில் உள்ளன எனவே அமைப்பின் மொத்த நேர்க்கோட்டு உந்தம் சுழியாகும். ![]() என்பது குண்டின் உந்தமாகவும்,
என்பது குண்டின் உந்தமாகவும், ![]() என்பது துப்பாக்கியின் உந்தமாகவும் கருதுக. இங்கு இரண்டும் ஓய்வு நிலையில் உள்ளன.
என்பது துப்பாக்கியின் உந்தமாகவும் கருதுக. இங்கு இரண்டும் ஓய்வு நிலையில் உள்ளன.
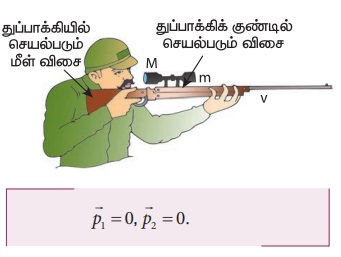
சுடுவதற்கு முன் மொத்த உந்தம் சுழி 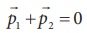 நேர்க்கோட்டு உந்த அழிவின்மை விதிப்படி, துப்பாக்கி சுட்ட பின்பும் மொத்த நேர்க்கோட்டு உந்தம் சுழி மதிப்பைப் பெற வேண்டும்.
நேர்க்கோட்டு உந்த அழிவின்மை விதிப்படி, துப்பாக்கி சுட்ட பின்பும் மொத்த நேர்க்கோட்டு உந்தம் சுழி மதிப்பைப் பெற வேண்டும்.
துப்பாக்கி சுடப்படும்போது, துப்பாக்கி முன்னோக்கிய திசையில் ஒரு விசையை குண்டின் மீது செலுத்தும். எனவே குண்டின் உந்தம் 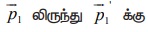 மாற்றமடையும். நேர்க்கோடு உந்த மாறா விதியின் காரணமாக துப்பாக்கியின் உந்தமும்
மாற்றமடையும். நேர்க்கோடு உந்த மாறா விதியின் காரணமாக துப்பாக்கியின் உந்தமும் ![]() விலிருந்து
விலிருந்து ![]() மாற்றமடையும். உந்த மாறா விதிப்படி
மாற்றமடையும். உந்த மாறா விதிப்படி 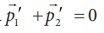 இதிலிருந்து
இதிலிருந்து 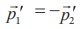 என அறியலாம். எனவே துப்பாக்கியின் உந்தம் துப்பாக்கிக் குண்டின் உந்தத்திற்கு எதிர்திசையில் இருக்கும்.
என அறியலாம். எனவே துப்பாக்கியின் உந்தம் துப்பாக்கிக் குண்டின் உந்தத்திற்கு எதிர்திசையில் இருக்கும்.
இதன் காரணமாகத்தான் துப்பாக்கி சுடப்பட்ட பின்பு, ![]() என்ற ஒரு உந்தத்துடன் பின்னோக்கி இயங்கும். இதற்கு ‘பின்னியக்க உந்தம்’ என்று பெயர். இந்த இயக்கம் உந்த மாறா விதிக்கு ஒரு எடுத்துக் காட்டு ஆகும்.
என்ற ஒரு உந்தத்துடன் பின்னோக்கி இயங்கும். இதற்கு ‘பின்னியக்க உந்தம்’ என்று பெயர். இந்த இயக்கம் உந்த மாறா விதிக்கு ஒரு எடுத்துக் காட்டு ஆகும்.
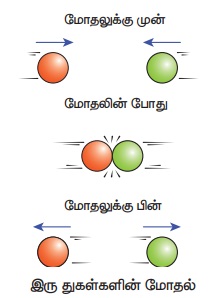
(2) ஓய்வு நிலையிலுள்ள ஒரு பொருள், மற்றும் அதை நோக்கிய திசையில் இயங்கும் பொருள் ஆகிய இரண்டு பொருட்களைக் கருதுக. இவை இரண்டும் ஒன்றுடன் ஒன்று மோதி, மோதலுக்குப்பின் தன்னிச்சையான திசையில் செல்கின்றன.
இந்நிகழ்வில், மோதலுக்கு முன்பு அமைப்பின் மொத்த நேர்க்கோட்டு உந்தம், இயக்கத்திலுள்ள பொருட்களின் தொடக்க நேர்க்கோட்டு உந்தத்திற்குச் சமமாகும். நேர்க்கோட்டு உந்த மாறா விதிப்படி, மோதலுக்கு பின்பும் அமைப்பின் மொத்த நேர்க்கோட்டு உந்தம் முன்னோக்கிய திசையில் செயல்படும். பின்வரும் படம் இதனை விளக்குகிறது.
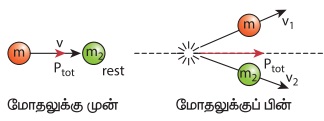
மோதலுக்கு முன்பு
பிரிவு 4.4 இல் இம்மோதல் பற்றிய விரிவான கணக்கீடுகள் வழங்கப்பட்டுள்ளன. இங்கு பின்வரும் கருத்தைப் புரிந்து கொள்வது பயனுள்ளதாக இருக்கும். மோதலுக்கு முன்பும், பின்பும் மொத்த உந்த வெக்டர் ஒரே திசையில் உள்ளது. இது மொத்த நேர்க்கோட்டு உந்தம் மோதலுக்கு முன்பும் பின்பும் ஒரு மாறிலி வெக்டர் என்பதை எளிமையாக விளக்குகின்றது. மோதலின்போது ஒவ்வொரு பொருளும் மற்ற பொருளின் மீது ஒரு விசையைச் செலுத்தும். இவ்விரண்டு பொருட்களையும் ஒரு அமைப்பு எனக் கருதினால், இவ்விரண்டு விசைகளும் அகவிசைகளாகும். எனவே இந்த அகவிசைகள் மொத்த நேர்க்கோட்டு உந்தத்தை மாற்றாது.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் கணத்தாக்கு விசை அல்லது கணத்தாக்கு
எடுத்துக்காட்டு 3.16
15m s-1 வேகத்தில் இயங்கும் 10 kg நிறையுடைய பொருள் சுவர் மீது மோதி
அ) 0.03 s
ஆ) 10 s ஆகிய நேர இடைவெளிகளில் ஓய்வுநிலையை அடைகிறது. இவ்விரண்டு நேர இடைவெளிகளிலும் பொருளின் கணத்தாக்கு மற்றும் பொருளின் மீது செயல்படும் சராசரி விசை ஆகியவற்றைக் காண்க.
தீர்வு
பொருளின் ஆரம்ப உந்தம்

இரண்டு நேர்வுகளிலும் பொருளின் கணத்தாக்கு சமம். ஆனால் பொருளின் மீது செயல்படும சராசரி விசை வெவ்வேறானவை.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் ஓய்வு நிலை உராய்வு
எடுத்துக்காட்டு 3.17
2 kg நிறையுடைய பொருளொன்று தளம் ஒன்றில் ஓய்வுநிலையில் உள்ளது என்க. பொருள் மற்றும் தளத்திற்கிடையேயான ஓய்வு நிலை உராய்வுக் குணகம் µs 0.8 எனில், அத்தளத்தின் மீது பொருளை நகர்த்துவதற்கு எவ்வளவு விசையைச் செலுத்த வேண்டும்.
தீர்வு
பொருள் ஓய்வு நிலையில் உள்ளதால், பொருளின் மீது செயல்படும் புவியீர்ப்பு விசை, அப்பொருள் வைக்கப்பட்டுள்ள தளமானது, பொருளின் மீது செலுத்தும் செங்குத்து விசையினால் சமன் செய்யப்படும்.

எனவே, பொருளைப் பரப்பின் மீது நகர்த்துவதற்குச் செலுத்த வேண்டிய புறவிசை, கீழே கொடுக்கப்பட்டுள்ள பெரும ஓய்வு நிலை உராய்வு விசையை விட அதிகமாக இருக்கவேண்டும்.

எடுத்துக்காட்டு 3.18
50 kg நிறையுடைய பொருள் தளம் ஒன்றில் ஓய்வுநிலையில் உள்ளது. அப்பொருளினை நகர்த்த அதன் மீது 5 N விசை செலுத்தப்படுகிறது. எனினும் பொருள் நகரவில்லை. இந்நிலையில் பொருள் வைக்கப்பட்டுள்ள தளம், பொருளின் மீது செலுத்தும் உராய்வு விசையைக் கண்டுபிடி.
தீர்வு
பொருள் ஓய்வு நிலையில் உள்ள போது, பொருளின் மீது செலுத்தப்படும் வெளிப்புற விசையும், பொருள் வைக்கப்பட்டுள்ள தளம் பொருளின்மீது செலுத்தும் உராய்வு விசையும் ஒன்றுக்கொன்று சமம் மற்றும் எதிரெதிராகச் செயல்படும்.
இவ்விரு விசைகளின் எண் மதிப்புகளும் சமமாகும்
f s = Fext
எனவே, பொருளின் மீது செயல்படும் ஓய்வு நிலை உராய்வு விசை

உராய்வு விசையின் திசை, வெளிப்புற விசையின் திசைக்கு Fext எதிர்த் திசையில் இருக்கும்.
எடுத்துக்காட்டு 3.19
7 kg மற்றும் 5 kg நிறையுடைய இரண்டு பொருட்கள் படத்தில் காட்டியுள்ளவாறு மேசையின் முனையில் பொருத்தப்பட்டுள்ள கப்பி ஒன்றின் வழியே செல்லும் மெல்லிய கயிற்றின் இரண்டு முனைகளில் இணைக்கப்பட்டுள்ளன. பொருளுக்கும், பொருள் வைக்கப்பட்டுள்ள பரப்புக்கும் இடையேயான ஓய்வு நிலை உராய்வுக் குணகத்தின் மதிப்பு 0.9 எனில் பரப்பின் மீது வைக்கப்பட்டிருக்கும் 7 kg நிறையுடைய m1 என்ற பொருள் நகருமா? அவ்வாறு நகரவில்லை எனில் m2 நிறையின் எம்மதிப்பிற்கு m1 நிறை நகரத் துவங்கும்?
தீர்வு
படத்தில் காட்டியவாறு m1 நிறையின் மீது நான்கு விசைகள் செயல்படுகின்றன
அ) எதிர்க்குறி y அச்சுத் திசையில் கீழ்நோக்கிச் செயல்படும் புவியீர்ப்பு விசை (m1g)
ஆ) நேர்க்குறி y அச்சுத்திசையில் மேல் நோக்கிச் செயல்படும் செங்குத்து விசை (N)
இ) m2 நிறையினால் நேர்க்குறி x அச்சுத்திசையில் செயல்படும் இழுவிசை
ஈ) எதிர்க்குறி × அச்சுத்திசை யில் செயல்படும் உராய்வு விசை
இங்கு, நிறை m1 எவ்விதமான செங்குத்து இயக்கத்தையும் மேற்கொள்ளவில்லை. எனவே, m1g = N
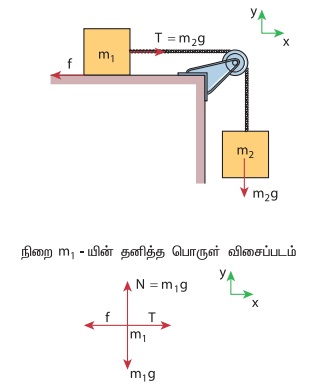
பரப்பின் மீது m1 நிறை நகர்கிறதா எனக் கண்டறிய, m1 நிறை வைக்கப்பட்டுள்ள பரப்பு, m1 நிறையின் மீது செலுத்தும் பெரும ஓய்வுநிலை உராய்வினைக் காண வேண்டும். நிறை m1 மீது செயல்படும் இழுவிசை, பெரும ஓய்வு நிலை உராய்வு விசையை விட அதிகமாக இருப்பின் பொருள் நகரத்துவங்கும்.
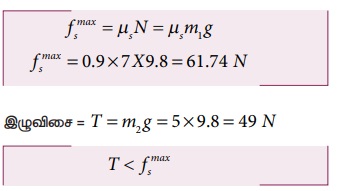
நிறை m1 மீது செயல்படும் இழுவிசை, ஓய்வு நிறை உராய்வை விடக் குறைவாக இருப்பதனால் நிறை m1 பரப்பின் மீது நகராது.
m1 நிறையை நகர்த்த T > fsmax இங்கு T = m2g
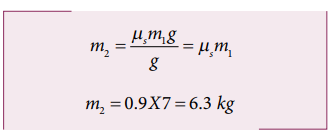
நிறை m2 மதிப்பு 6.3 kg விட அதிகம் எனில், நிறை m1 பரப்பின் மீது நகரத் தொடங்கும்.
பரப்பில் எவ்வித உராய்வும் இல்லை எனில் அதாவது வழுவழுப்பான பரப்பு எனில், நிறை m2 வின் எந்தவொரு மதிப்பிற்கும் நிறை m1 பரப்பின் மீது நகர்ந்து செல்லும் என்பதை இங்கு நினைவில் கொள்ள வேண்டும்.
சோடிப்பொருட்களின் பரப்புகளுக்கிடையேயான ஓய்வு நிலை உராய்வுக் குணகத்தின் மதிப்பு, அட்டவணை 3.1 இல் காட்டப்பட்டுள்ளது பனிக்கட்டித் துண்டுகளுக்கிடையேயான ஓய்வு நிலை உராய்வுக் குணகம் மிகக்குறைந்த மதிப்பைப் பெற்றுள்ளதை இங்கு கவனிக்கவும். ஒரு பனிக்கட்டித்துண்டை மற்றொரு பனிக்கட்டித் துண்டின்மீது எளிதாக நகர்த்த முடியும் என்பதை இது சுட்டிக்காட்டுகிறது.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் சறுக்குக்கோணம்
எடுத்துக்காட்டு 3.20
கிடைத்தளத்துடன் 60° கோணத்தில் சாய்ந்துள்ள, சாய்தளத்தின்மீது m நிறையுள்ள பொருளொன்று வைக்கப்பட்டுள்ளது. அப்பொருள் g/2 என்ற முடுக்கத்துடன் கீழ்நோக்கிச் சறுக்கி சென்றால் அப்பொருளின் இயக்க உராய்வு குணகத்தைக் காண்க.
தீர்வு
பொருள் சாய்தளத்தில் சறுக்கிச் செல்லும்போது இயக்க உராய்வு ஏற்படுகிறது.
பொருளின் மீது கீழ்க்கண்ட விசைகள் செயல்படுகின்றன அவை தளத்திற்கு செங்குத்தாக செயல்படும். செங்குத்து விசை, கீழ்நோக்கிச் செயல்படும் புவியீர்ப்புவிசை மற்றும் தளத்திற்கு இணையாகச் செயல்படும் இயக்க உராய்வு விசை
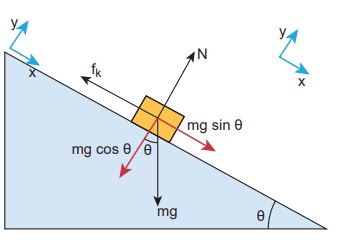
x அச்சுத்திசையில்
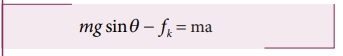
ஆனால் a = g / 2
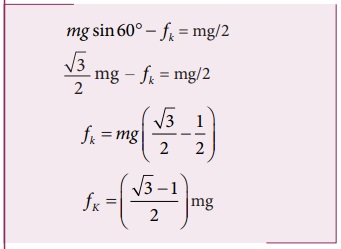
y- அச்சுத்திசையில் எவ்வித இயக்கமும் இல்லை. எனவே செங்குத்து விசை (N), mg cosθ என்ற கூறினால் சமன் செய்யப்படுகிறது.
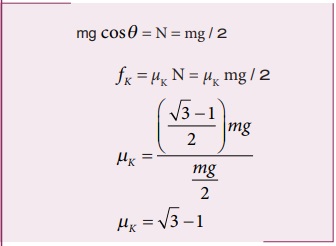
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் உராய்வு
எடுத்துக்காட்டு 3.21
பொருளொன்று மாறாத் திசைவேகத்தில் கிடைத்தளப் பரப்பில் இயங்குகின்றது எனக் கருதுக. வெளிப் புறவிசை அப்பொருளின் மீது செயல்பட்டு அதனை மாறாத் திசைவேகத்தில் இயக்கினால், அப்பொருளின் மீது செயல்படும் தொகுபயன் விசையின் மதிப்பு என்ன?
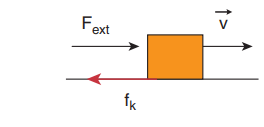
தீர்வு
பொருள் மாறாத் திசைவேகத்தில் இயங்கும்போது அப்பொருளின் முடுக்கம் சுழி. நியூட்டனின் இரண்டாம் விதிப்படி பொருளின்மீது எவ்விதமான தொகுபயன் விசையும் செயல்படவில்லை. வெளிப்புற விசையானது இயக்க உராய்வினால் சமன் செய்யப்படுகிறது.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் மையநோக்கு விசை
எடுத்துக்காட்டு 3.22
0.25 kg நிறையுடைய கல் ஒன்று கயிற்றின் முனையில் கட்டப்பட்டு 2 m s-1 வேகத்தில் 3 m ஆரமுடைய சீரானவட்ட இயக்கத்தை மேற்கொள்கிறது. கல்லின் மீது செயல்படும் இழுவிசையினைக் கண்டுபிடி
தீர்வு:
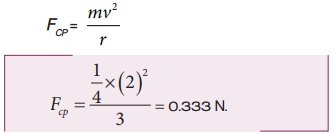
எடுத்துக்காட்டு 3.23
நிலா, புவியினை வட்டப்பாதைக்கு ஒத்த ஒரு பாதையில் 27.3 நாட்களில் முழுமையாகச் சுற்றி வருகிறது. புவியின் ஆரம் 6.4 × 106 m எனில் நிலாவின் மீது செயல்படும் மையநோக்கு முடுக்கத்தைக் காண்க.
தீர்வு
மையநோக்கு முடுக்கம் a = v2/r. இச் சமன்பாடு வெளிப்படையாகவே நிலவின் வேகத்தைச் சார்ந்தது. இந்த வேகத்தை கணக்கிடுவது சற்றுக் கடினமாகும். எனவே நாம் பின்வரும் சமன்பாட்டினைப் பயன்படுத்தலாம்.
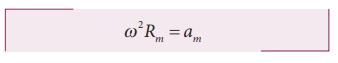
இங்கு am என்பது புவியின் ஈர்ப்பு விசையினால், நிலா பெறும் மைய நோக்கு முடுக்கமாகும்.
ω என்பது கோணத் திசைவேகம்
Rm என்பது புவியிலிருந்து நிலா வரை உள்ள தொலைவு. இது புவியின் ஆரத்தைப் போன்று 60 மடங்காகும்.

புவியை நோக்கி நிலாவின் மையநோக்கு முடுக்கம் 0.00272 m s-2
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் சரி சமமான வட்டச் சாலையில் செல்லும் வாகனம்
எடுத்துக்காட்டு 3.24
ஆரம் 10 m மற்றும் நிலை உராய்வுக் குணகம் 0.81 கொண்ட சரிசமமான வட்டவடிவச் சாலை ஒன்றைக் கருதுக. அச்சாலையில் மூன்று கார்கள் (A,B மற்றும் C) முறையே 7 m s-1, 8 m s-1 , 10 m s-1 வேகத்தில் செல்கின்றன. இவற்றுள் எந்த கார் வட்ட வடிவச்சாலையில் செல்லும் போது சறுக்கி விழும்? (g = 10 m s-2)
தீர்வு
சரி சமமான வட்டச்சாலையில் செல்லும் வாகனம் சறுக்காமல் இருக்கத் தேவையான நிபந்தனை, வாகனத்தின் வேகம் (v) இன் மதிப்பு 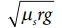 ஐ விடக் குறைவாகவோ அல்லது சமமாகவோ இருக்க வேண்டும்.
ஐ விடக் குறைவாகவோ அல்லது சமமாகவோ இருக்க வேண்டும்.
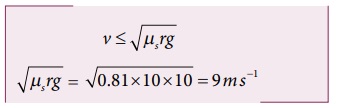
C காரினைப் பொருத்தவரை 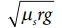 இன் மதிப்பு காரின் வேகம் v ஐ விடக் குறைவு. கார் A மற்றும் B இரண்டும் பாதுகாப்பாக வளையும், ஆனால் கார் C இன் வேகம், நிர்ணயிக்கப்பட்ட வேகத்தை விட (
இன் மதிப்பு காரின் வேகம் v ஐ விடக் குறைவு. கார் A மற்றும் B இரண்டும் பாதுகாப்பாக வளையும், ஆனால் கார் C இன் வேகம், நிர்ணயிக்கப்பட்ட வேகத்தை விட (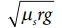 ) அதிகமாக உள்ளதால் அது சறுக்கி விடும்.
) அதிகமாக உள்ளதால் அது சறுக்கி விடும்.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் வெளிவிளிம்பு உயர்த்தப்பட்ட சாலை
எடுத்துக்காட்டு 3.25
20 m ஆரமுடைய வட்டச்சாலையைக் கருதுக. அதன் வெளிவிளிம்புக் கோணம் 15°என்க. அச்சாலையில் செல்லும் வாகனம் நழுவி விழாமல் பாதுகாப்பாக வளைவதற்குத் தேவையான வேகத்தைக் காண்க.
தீர்வு
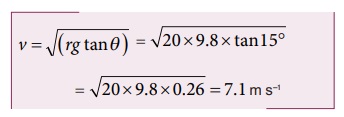
சறுக்கி விழாமல் பாதுகாப்பாக வளைவதற்குத் தேவையான வேகம் = 7.1 m s-1
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் புவியின் சுழற்சியால் ஏற்படும் மையவிலக்கு விசை
எடுத்துக்காட்டு 3.26
சென்னையிலுள்ள 60 kg நிறையுடைய மனிதரின் மீது செயல்படும் மையவிலக்கு விசையைக் காண்க.
(கொடுக்கப்பட்டவை: சென்னையில் குறுக்குக் கோடு θ = 13°)
தீர்வு
மையவிலக்கு விசை Fcf = mω2 R cosθ
புவியின் கோணத் திசைவேகம் 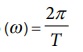
இங்கு T என்பது புவியின் அலைவு நேரம் (24 மணிநேரம்)
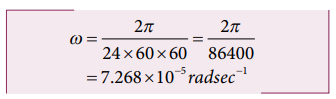
புவியின் ஆரம் R = 6400 km = 6400×103 m
சென்னையின் குறுக்கு கோடு (Latitude) = 13°
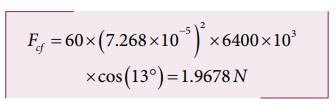
60 kg நிறையுடைய மனிதரொருவர் உணரும் மைய விலக்கு விசை தோராயமாக 2 நியூட்டனாகும். ஆனால் புவியின் ஈர்ப்பு விசையின் காரணமாக 60 kg நிறையுடைய அம்மனிதர் உணரும் விசை = mg = 60 × 9.8 = 588 N. இந்த விசைமையவிலக்கு விசையை விட மிக அதிகம்.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் மையநோக்கு விசை
எடுத்துக்காட்டு 3.22
0.25 kg நிறையுடைய கல் ஒன்று கயிற்றின் முனையில் கட்டப்பட்டு 2 m s-1 வேகத்தில் 3 m ஆரமுடைய சீரானவட்ட இயக்கத்தை மேற்கொள்கிறது. கல்லின் மீது செயல்படும் இழுவிசையினைக் கண்டுபிடி
தீர்வு:
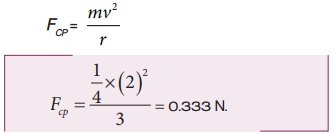
எடுத்துக்காட்டு 3.23
நிலா, புவியினை வட்டப்பாதைக்கு ஒத்த ஒரு பாதையில் 27.3 நாட்களில் முழுமையாகச் சுற்றி வருகிறது. புவியின் ஆரம் 6.4 × 106 m எனில் நிலாவின் மீது செயல்படும் மையநோக்கு முடுக்கத்தைக் காண்க.
தீர்வு
மையநோக்கு முடுக்கம் a = v2/r. இச் சமன்பாடு வெளிப்படையாகவே நிலவின் வேகத்தைச் சார்ந்தது. இந்த வேகத்தை கணக்கிடுவது சற்றுக் கடினமாகும். எனவே நாம் பின்வரும் சமன்பாட்டினைப் பயன்படுத்தலாம்.
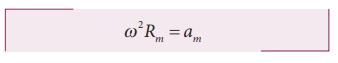
இங்கு am என்பது புவியின் ஈர்ப்பு விசையினால், நிலா பெறும் மைய நோக்கு முடுக்கமாகும்.
ω என்பது கோணத் திசைவேகம்
Rm என்பது புவியிலிருந்து நிலா வரை உள்ள தொலைவு. இது புவியின் ஆரத்தைப் போன்று 60 மடங்காகும்.

புவியை நோக்கி நிலாவின் மையநோக்கு முடுக்கம் 0.00272 m s-2
இந்தக் கணக்கீடு நியூட்டனாலேயே செய்யப்பட்டதாகும். இம்முடிவினை நாம் பிற்பகுதியில் கற்கவுள்ள அலகு 6 இல் பயன்படுத்துவோம்.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் சரி சமமான வட்டச் சாலையில் செல்லும் வாகனம்
எடுத்துக்காட்டு 3.24
ஆரம் 10 m மற்றும் நிலை உராய்வுக் குணகம் 0.81 கொண்ட சரிசமமான வட்டவடிவச் சாலை ஒன்றைக் கருதுக. அச்சாலையில் மூன்று கார்கள் (A,B மற்றும் C) முறையே 7 m s-1, 8 m s-1 , 10 m s-1 வேகத்தில் செல்கின்றன. இவற்றுள் எந்த கார் வட்ட வடிவச்சாலையில் செல்லும் போது சறுக்கி விழும்? (g = 10 m s-2)
தீர்வு
சரி சமமான வட்டச்சாலையில் செல்லும் வாகனம் சறுக்காமல் இருக்கத் தேவையான நிபந்தனை, வாகனத்தின் வேகம் (v) இன் மதிப்பு 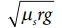 ஐ விடக் குறைவாகவோ அல்லது சமமாகவோ இருக்க வேண்டும்.
ஐ விடக் குறைவாகவோ அல்லது சமமாகவோ இருக்க வேண்டும்.
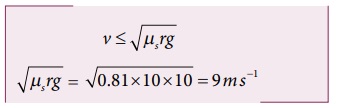
C காரினைப் பொருத்தவரை 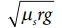 இன் மதிப்பு காரின் வேகம் v ஐ விடக் குறைவு. கார் A மற்றும் B இரண்டும் பாதுகாப்பாக வளையும், ஆனால் கார் C இன் வேகம், நிர்ணயிக்கப்பட்ட வேகத்தை விட (
இன் மதிப்பு காரின் வேகம் v ஐ விடக் குறைவு. கார் A மற்றும் B இரண்டும் பாதுகாப்பாக வளையும், ஆனால் கார் C இன் வேகம், நிர்ணயிக்கப்பட்ட வேகத்தை விட (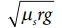 ) அதிகமாக உள்ளதால் அது சறுக்கி விடும்.
) அதிகமாக உள்ளதால் அது சறுக்கி விடும்.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் வெளிவிளிம்பு உயர்த்தப்பட்ட சாலை
எடுத்துக்காட்டு 3.25
20 m ஆரமுடைய வட்டச்சாலையைக் கருதுக. அதன் வெளிவிளிம்புக் கோணம் 15°என்க. அச்சாலையில் செல்லும் வாகனம் நழுவி விழாமல் பாதுகாப்பாக வளைவதற்குத் தேவையான வேகத்தைக் காண்க.
தீர்வு
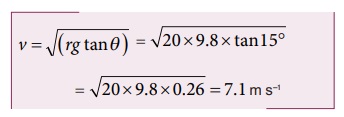
சறுக்கி விழாமல் பாதுகாப்பாக வளைவதற்குத் தேவையான வேகம் = 7.1 m s-1
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் புவியின் சுழற்சியால் ஏற்படும் மையவிலக்கு விசை
எடுத்துக்காட்டு 3.26
சென்னையிலுள்ள 60 kg நிறையுடைய மனிதரின் மீது செயல்படும் மையவிலக்கு விசையைக் காண்க.
(கொடுக்கப்பட்டவை: சென்னையில் குறுக்குக் கோடு θ = 13°)
தீர்வு
மையவிலக்கு விசை Fcf = mω2 R cosθ
புவியின் கோணத் திசைவேகம் 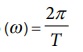
இங்கு T என்பது புவியின் அலைவு நேரம் (24 மணிநேரம்)
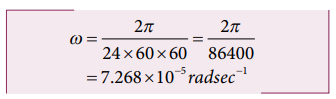
புவியின் ஆரம் R = 6400 km = 6400×103 m
சென்னையின் குறுக்கு கோடு (Latitude) = 13°
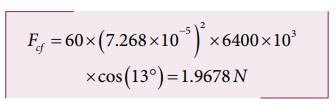
60 kg நிறையுடைய மனிதரொருவர் உணரும் மைய விலக்கு விசை தோராயமாக 2 நியூட்டனாகும். ஆனால் புவியின் ஈர்ப்பு விசையின் காரணமாக 60 kg நிறையுடைய அம்மனிதர் உணரும் விசை = mg = 60 × 9.8 = 588 N. இந்த விசைமையவிலக்கு விசையை விட மிக அதிகம்.