தகவல் செயலாக்கம் | முதல் பருவம் அலகு 6 | 7ஆம் வகுப்பு கணக்கு - நாற்சதுர இணை (Tetromino) | 7th Maths : Term 1 Unit 6 : Information Processing

7ஆம் வகுப்பு கணக்கு : முதல் பருவம் அலகு 6 : தகவல் செயலாக்கம்

நாற்சதுர இணை (Tetromino)

நாற்சதுர இணைகளைப் (Tetrominos) பற்றி அறிந்துகொள்ள வேண்டுமானால் இருசதுர இணைகள் (Dominos) மற்றும் முச்சதுர இணைகளைப்(Trinominos) பற்றிய புரிதல் அவசியம்.

1 செ.மீ × 1 செ.மீ பக்க அளவுள்ள இரு சதுரங்களை அதன் விளிம்புகளில் ஒன்றோடொன்று இணைக்கும் போது அமையும் வடிவத்தையே இருசதுர இணைகள் என்கிறோம். இருசதுர இணையைக் கிடைமட்டமாகவோ அல்லது செங்குத்தாகவோ இணைக்கும்போது அருகில் அடைப்புக்குறிக்குள் காட்டப்பட்டுள்ள வடிவங்களைப் போன்று அமைகிறது.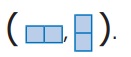

இதனைப்போன்றே, மூன்று சதுரங்களை அதன் விளிம்புகளில் ஒன்றோடொன்று இணைக்கும்போது அமையும் வடிவத்தையே முச்சதுர இணை என்கிறோம். முச்சதுர இணையைக் கிடைமட்டமாகவோ அல்லது செங்குத்தாகவோ இணைக்கும்போது அருகில் அடைப்புக் குறிக்குள் காட்டப்பட்டுள்ள வடிவங்களைப் போன்று அமைகிறது.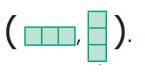

மூன்று சதுரங்களைக் கொண்டு இவ்விரு விதங்களில் மட்டும்தான் இணைக்க முடியுமா என்றால், இல்லை; சிறிது மாற்றி, வேறு விதங்களில் இணைத்துப் பார்க்கும் போது நம்மால் அருகில் அடைப்புக் குறிக்குள் காட்டப்பட்டுள்ள நான்கு விதமான வடிவங்களை அமைக்க முடிகிறது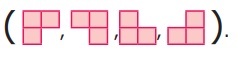

இருசதுர இணை மற்றும் முச்சதுர இணை வடிவங்களில் முயற்சித்தது போன்று 1 செ.மீ × 1 செ.மீ பக்க அளவுள்ள நான்கு சதுரங்களை, அவற்றின் விளிம்புகளில் ஒன்றோடொன்று இணைத்தால் அருகில் அடைப்புக்குறிக்குள் காட்டப்பட்டுள்ள வடிவங்களைப் போன்று அமைக்கலாம்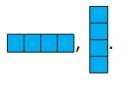

நான்கு சதுரங்களை இணைக்க வேறு ஏதேனும் வழிகள் உள்ளனவா? ஆம், அவற்றைப் பற்றி இப்பாடத்தில் கற்றுக் கொள்வோம்.

சூழ்நிலை 1

ஆசிரியர், மாணவர்களை ஐந்து குழுக்களாகப் பிரித்து ஒவ்வொரு குழுவினரிடத்திலும் 1 செ.மீ × 1 செ.மீ பக்க அளவுள்ள 20 சதுர வில்லைகளை வழங்கினார். மாணவர்களை வெவ்வேறு விதங்களில் நான்கு சதுர வில்லைகளின் விளிம்புகளை ஒன்றோடொன்று இணைக்குமாறு கூறினார். ஒவ்வொரு குழுவினரும் மற்றவர்கள் உருவாக்கிய வடிவங்களை ஒப்பிட்டு, பொதுவான வடிவங்களை மட்டும் கரும்பலகையில் வரையச் செய்தார். எத்தனை விதமான வடிவங்கள் மாணவர்களுக்குக் கிடைத்தன?

நம்மால் அருகில் அடைப்புக்குறிக்குள் காட்டப்பட்டுள்ள ஐந்து வெவ்வேறு விதமான வடிவங்களை மட்டுமே பெறமுடிகிறது அல்லவா?

இவ்வடிவங்களைச் சுழற்றும்போது கிடைக்கும் வடிவங்கள் கீழே படம் 6.7 இல் கொடுக்கப்பட்டுள்ளன:

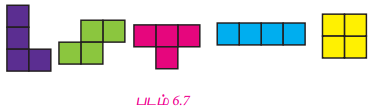
மேற்காணும் வகைகளில் 1 செ.மீ × 1 செ.மீ பக்க அளவுள்ள நான்கு சதுரங்களை அதன் விளிம்புகளில் ஒன்றோடொன்று இணைக்கும்போது நாம் பெறும் வடிவங்களே "நாற்சதுர இணைகள் “(TETROMINOS)" எனப்படும்.

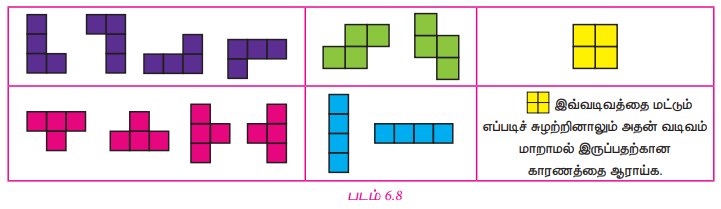
“டிரை' என்ற வார்த்தை மூன்று எனப் பொருள்படும். மூன்று சதுரங்களை இணைப்பதே முச்சதுர இணை என அழைக்கப்படுகிறது. 'டெட்ரா’ என்பது நான்கு எனப் பொருள்படும். நான்கு சதுரங்களை இணைப்பதே நாற்சதுர இணை என அழைக்கப்படுகிறது.

இவற்றை முயல்க

கொடுக்கப்பட்டுள்ள ஐந்து நாற்சதுர இணை வடிவங்களை ஒரே ஒரு முறை பயன்படுத்திக் கீழே கொடுக்கப்பட்டுள்ள வடிவத்தை உருவாக்குக.

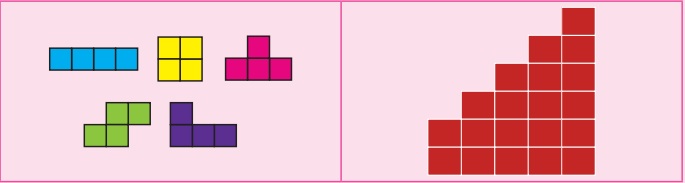
1. நாற்சதுர இணைகளைப் பயன்படுத்திச் செவ்வக வடிவங்களை நிரப்புதல்

சூழ்நிலை 2

ஐந்து விதமான நாற்சதுர இணைகளையும் ஒருமுறை பயன்படுத்தி உங்களால் செவ்வக வடிவத்தை நிரப்பமுடியுமா? எனில், முடியவில்லை இல்லையா? கீழே படம் 6.19 முதல் படம் 6.12 (முழுமையாக) வரையில் கொடுக்கப்பட்டுள்ள செவ்வகங்களை உற்று நோக்கவும், நாற்சதுர இணைகள் அதன் விளிம்புகளில் ஒன்றோடொன்று இணைக்கப்பட்டிருப்பதைக் கவனிக்கவும். X குறியிடப்பட்டுள்ள கட்டங்கள் நாற்சதுர இணை வடிவங்களால் நிரப்பப்படவில்லை. மாறாகச் சில நாற்சதுர இணை வடிவங்களின் பகுதிகள் செவ்வகத்தைவிட்டு வெளிப்புறமாக அமைந்துள்ளதால் செவ்வக வடிவம் முழுமை அடையவில்லை என்பதும் இதன் மூலம் புலப்படுகிறது.

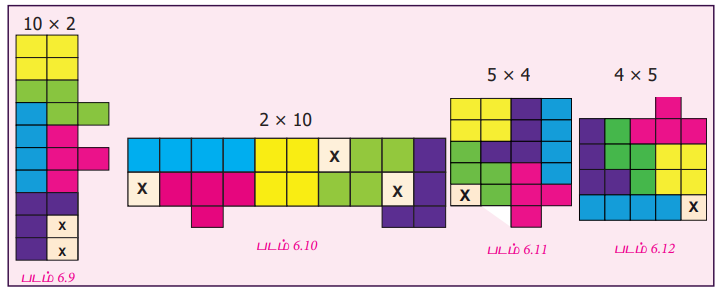
மொத்தமாக, நான்கு சதுரங்களைக் கொண்ட ஐந்து நாற்சதுர இணைகளை இணைக்கும்போது, 20 சதுரங்கள், உருவாகின்றன இந்த 20 சதுரங்களைப் பயன்படுத்தி 1 × 20, 20 × 1, 10 × 2, 2 × 10, 5 × 4 மற்றும் 4 × 5 என்ற அளவுகள் கொண்ட செவ்வகங்களை உருவாக்க முடியும்.

நம்மால், முழுமையாக ஐந்து நாற்சதுர இணைகளை ஒருமுறை மட்டும் பயன்படுத்திச் செவ்வகத்தை நிரப்பமுடியவில்லை என்பது ஏன் எனத் தெரியுமா? காரணத்தை அறிந்துகொள்ள ஐந்து நாற்சதுர இணைகளையும் கீழே உள்ள படம் 6.13 இல் கொடுக்கப்பட்டுள்ளதைப் போல் எடுத்துக்கொள்க.

ஐந்தில், நான்கு நாற்சதுர இணைகளில் வண்ணமிட்ட சதுரங்களும், வண்ணமிடப்படாத சதுரங்களும் ஒரே அளவில் உள்ளன. ஆனால், , என்ற நாற்சதுர இணையில் மட்டும் வண்ண மிட்ட சதுரங்களும், வண்ணமிடப்படாத சதுரங்களும் சம அளவில் இல்லை. இதன் காரணமாகவே, நம்மால், முழுமையாக ஐந்து நாற்சதுர இணைகளையும் ஒருமுறை மட்டும் பயன்படுத்திச் செவ்வகத்தை நிரப்ப முடியவில்லை .

அதற்கு மாறாக, ஐந்து நாற்சதுர இணைகளை இருமுறை பயன்படுத்தும்போது படம் 6.14 மற்றும் படம் 6.15 இல் உள்ளதைப் போன்று 5 × 8, 4 × 10 போன்ற வரிசை அமைப்புகளுள்ள செவ்வகங்களை நம்மால் முழுமையாக நிரப்ப முடிகிறது.

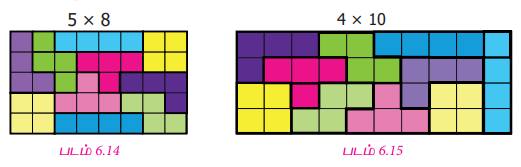
இக்கருத்து, நம் அன்றாட வாழ்வில், தரையில் சதுர ஓடுகளைப் பதித்தல், குறைந்த அளவு பெட்டிக்குள் அதிகப் பொருள்களை அடக்குதல் போன்ற பல விஷயங்களில் பயனுள்ளதாக அமைந்துள்ளது.

இவற்றை முயல்க

1. ஐந்து நாற்சதுர இணைகளையும் ஒருமுறை பயன்படுத்திக் கொடுக்கப்பட்டுள்ள செவ்வக வடிவங்களை நிரப்புக.

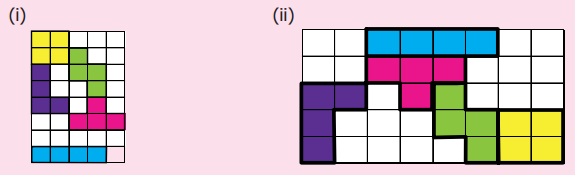
விடை :

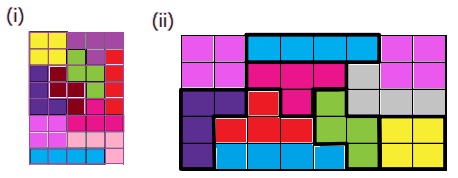
2. மாதிரி படம் 6.16 இல் நாற்சதுர இணை ‘’ 4 × 4 சதுர வடிவக் கட்டத்தில் முழுவதுமாக நிரப்பப்பட்டுள்ளது. அதனைப்போன்று, மற்ற நாற்சதுர இணைகளையும் கொடுக்கப்பட்டுள்ள படம் 6.17 முதல் படம் 6.20 வரையிலான 4 × 4 சதுர வடிவக் கட்டங்களில் நிரப்புக. மேலும், எந்த நாற்சதுர இணையைக் கொண்டு ( )4 × 4 சதுர வடிவக் கட்டத்தை நிரப்ப முடியவில்லை என்பதையும் காண்க.

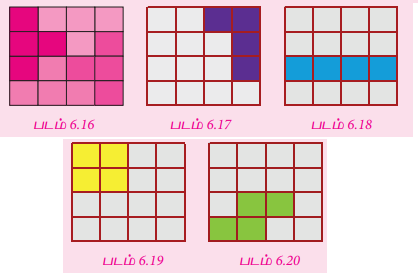
விடை :

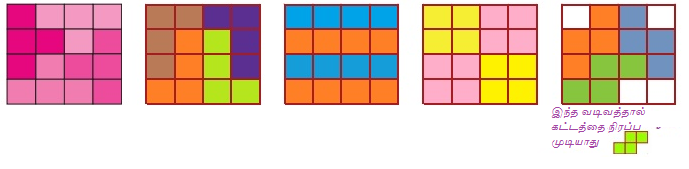
எடுத்துக்காட்டு 6.1

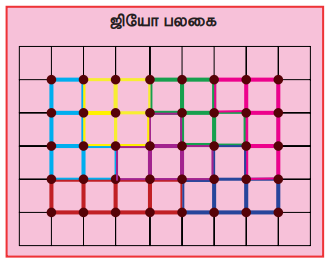
கொடுக்கப்பட்டுள்ள படம் 6.21 காட்சிப் பேழையில் நாற்சதுர இணை வடிவங்களைக் கண்டு பிடித்து, ஜியோ பலகையில் இரப்பர்பட்டை (rubberband)யைப் பயன்படுத்தி மேலே கண்ட வடிவங்களை வடிவமைத்துக் காட்டுக.

தீர்வு

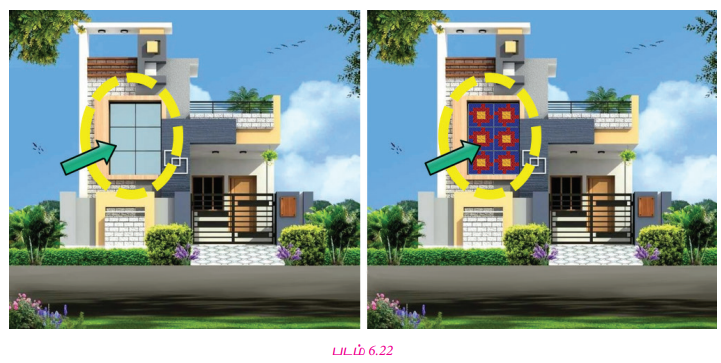
எடுத்துக்காட்டு 6.2

இராகவன் தனது வீட்டின் முகப்புத் தோற்றத்தினைப் படம் 6.22 இல் சுட்டிக்காட்டியுள்ளவாறு கொடுக்கப்பட்டுள்ள நாற்சதுர இணை வடிவங்களால் உருவான சதுர ஓடுகளைக்கொண்டு மாற்றியமைக்க முற்படுகிறார் எனில்,

1. ஒரு சதுர ஓட்டில் எத்தனை நாற்சதுர இணைகள் உள்ளன?

2. ஒரு சதுர ஓட்டின் விலை 52 ரூபாய் எனில், இராகவன் தனது வீட்டின் முகப்புத் தோற்றத்தினை மாற்றியமைப்பதற்குத் தேவையான ஓடுகள் வாங்க எவ்வளவு தொகை செலவாகும் (படம். 6.22)

தீர்வு

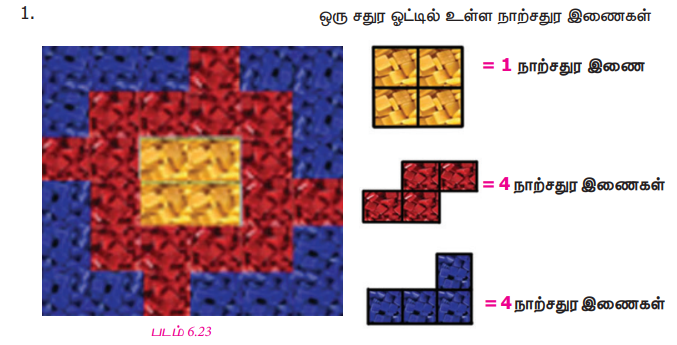
ஒரு சதுர ஓட்டில் உள்ள நாற்சதுர இணைகள்

ஆகவே, ஒரு சதுர ஓட்டில் 9 நாற்சதுர இணைகள் உள்ளன.

2. ஒரு சதுர ஓட்டின் விலை ₹ 52 எனில், வீட்டின் முகப்புத் தோற்றத்தினை மாற்றியமைப்பதற்கு மொத்தம் 6 சதுர ஓடுகள் தேவைப்படுகின்றன.

எனவே, இராகவனுக்கு சதுர ஓடுகள் வாங்கச் செலவாகும் தொகை = 6 × 52

= ₹ 312 ஆகும்.

Tags : Information Processing | Term 1 Chapter 6 | 7th Maths தகவல் செயலாக்கம் | முதல் பருவம் அலகு 6 | 7ஆம் வகுப்பு கணக்கு.

7th Maths : Term 1 Unit 6 : Information Processing : Tetromino Information Processing | Term 1 Chapter 6 | 7th Maths in Tamil : 7th Standard Tamil Medium School Samacheer Book Back Questions and answers, Important Question with Answer. 7ஆம் வகுப்பு கணக்கு : முதல் பருவம் அலகு 6 : தகவல் செயலாக்கம் : நாற்சதுர இணை (Tetromino) - தகவல் செயலாக்கம் | முதல் பருவம் அலகு 6 | 7ஆம் வகுப்பு கணக்கு : 7 ஆம் வகுப்பு புத்தகம் கேள்விகள் மற்றும் பதில்கள்.